The Monty Hall Problem
The Monty Hall Problem is one of the most famous problems in probability theory. This problem is named after Monty Hall, the host of the television game show Let’s Make a Deal. It is a great problem to show students, not only because of the math involved, but also because of the story behind it. The reason why the Monty Hall Problem became so famous is that it appeared in an issue of Parade magazine as a problem posed to Marilyn vos Savant, a Guinness Book of World Records holder for the highest IQ. A reader wrote in describing a situation in which a game show contestant has a chance to pick one of three doors. Goats are behind two of the doors and a brand new car is behind the third door. After the contestant chooses, the host, who knows what is behind each door, then opens one of the doors the contestant didn’t pick to reveal a goat. The million dollar (or however much a brand new car is worth minus the taxes one must pay for it) question is, should the contestant stick with the original door or switch to the other remaining one? Vos Savant, being the smartest person in the world (or so says an Irish brewing company), said the contestant should switch and gave a precise and clear explanation. Her answer compelled many people to write in and say she was wrong. They believed that there was no incentive to switch because at this point you are down to two doors so there’s a 50/50 chance of getting the car.
This seems like the obvious answer. It is in fact what I expect most of my students to say when presented with this problem. But here’s the startling fact: people with PhDs in mathematics wrote in and chided Marilyn for answering incorrectly. Marilyn knew she was right, took the criticism well, and gave another explanation of why the contestant should switch. But apparently it was not good enough because even more mathematicians wrote saying she was mistaken, and some of them were downright snarky. Not one to back down, Marilyn tried a third explanation and asked math classes to try the experiment out and send in their results. Apparently this is what she should have done from the start because once people simulated the situation they saw that it worked out in their favor to switch. This is such a great story because it really shows you that probability can be counterintuitive, even for mathematicians!
What Marilyn kept stressing was the fact that the host knew what was behind each door and so he would never open the door with the car. This fact is what completely changes the problem. Here is one way you can explain the solution to this problem. Originally there are three doors so each door has one-third chance of having the car. This also means that the other two doors together have a two-thirds chance of having the car. Since the host knows what is behind each door, he opens a door that has a goat behind it. Now your original door still has that same one-third chance of having the car but that other two-thirds probability is now transferred to the remaining door. Well then heck yeah you should switch because you have a greater chance to get the (brand new) car. If you do end up with a goat door, I don’t think they let you keep the goat.
This problem is actually a simplified version of what happened on Let’s Make a Deal. On the show Monty was always wheeling and dealing so usually he would offer you money for your door or some other shenanigans. There was an article in The New York Times entitled “Behind Monty Hal’s Doors: Puzzle, Debate and Answer?” that discusses this story and includes commentary from Monty. I like to have my students read this article.
Begin this activity by explaining what The Monty Hall Problem is and ask the class to think about what they would do in this situation. Give them a few minutes to think about it or discuss with a partner. Take a class poll to see who would stick and who would switch. Ask one sticker and one switcher to explain why they chose that answer. Next, have students get into pairs with one acting as the host and one student acting as the contestant. If you have a groups of three the remaining student can keep track of the results. The host will be given two goat cards and one car card. He will place these cards facedown while the contestant looks away. Then the contestant will choose one of the cards. The host will then turn over one of the remaining cards that has a goat and the contestant will decide to stick or switch. Have students run through ten trials like this and keep track of their results in a table. Compile everyone’s results. I used an Excel sheet to do this. Once a group finished I had them enter values for how many times the contestant stuck, how many times they stuck and won, total times switching, and how many times they switched and won. I had the formulas in to calculate the totals for each of these columns and the percentage they won by sticking and the percentage won by switching. It wasn’t exact, but we did see around two-thirds of the times when students switched they won the car and one-third of the time they didn’t switch they won the car. At this point you can explain the solution.
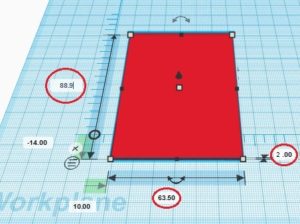
To make the cards used in this activity I first looked up the dimensions of a playing card. They are 2.5 inches by 3.5 inches. I converted these to 63.5 mm by 88.9 mm. In TinkerCad I created two boxes with these dimensions and a height of 2 mm.
Next, I drew pictures of a goat and a car and scanned them in.

I then converted these images to SVG files and uploaded them in TinkerCad. Since the cards will be face down I don’t want the images to stick out so instead I made them as indentations. To do this I made them holes. I didn’t want the image to go all the way through the card so I raised the goat and car by 1 mm and then grouped the box with each object.

Modular arithmetic
For this activity students will work in groups. Each group is given a worksheet. The worksheet is self-guided and has all the information they need on it, but you may choose to go over parts of it together. This topic is not explicitly listed as part of the Common Core Standards. It can be done at any point after students know how to divide and find remainders. The last problem on the worksheet is at a high school level, but that question can easily be dropped to make this activity more suitable for younger students. It will allow students to get a better grasp of what it means for two numbers to be congruent in mod n, and having the physical 3D model will help make the definition more concrete and memorable.
Day 1 gives some quick explorations of remainders and leads to discovering that the possible remainders when dividing by a number n is 0 to n-1. Then, students will use a spinner manipulative that looks like this.

You can have students design their own spinner, or you can make the spinners on your own and have them ready for each group. Having students design their own spinner will give them some ownership of the activity, but it will save time to just give them the spinners pre-made. This design is fairly easy to make. For the spinner I made the diameter of the open circle a little bigger than the diameter of the cylinder it went around (9.6 mm and 9 mm, respectively). For the spinner I used a cylinder with diameter 15.1mm and then created a cylinder hole in the center with diameter 9.6 mm.
On the second day students use their clocks to practice finding remainders. They then learn the congruent notation and do practice problems using it.
The worksheet and solutions can be found here.
