What is a Subsequence?

Well, formally:

A sequence t_k, is a subsequence of a sequence S_n if for t_k=〖S_n〗_k ,k≥0.

Informally, a subsequence is a part or piece of our main sequence.

We’ve seen at this point that some sequences are very messy. Some are convergent, some are divergent, some are monotonically increasing or decreasing, and some are just bounded to name a few. Subsequences allow us to make our way through an otherwise messy sequence and observe some of its nicer behavior.

It is important to note, though, that in a subsequence, the indices must be increasing, E.g., we can’t cherry pick the order of my subsequence. Say we have S_n where n goes from 1 to 100. We can’t just say that if we take S_25,S_12,S_21 I get a subsequence that converges to some limit L. We must choose terms such that k is increasing, so in this case it would have to be S_12,S_21,S_25. So while the sequence itself may be increasing or decreasing, what matters is that our k is increasing.

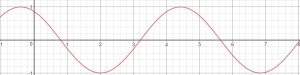
Say we take the above sequence, S_n=sin⁡(13x+21)/10. We can see that sin is not convergent, but we can see that it is bounded, so is there a subsequence we can find that is perhaps convergent to some limit?
Well, considering what we know, we can safely say that the sin function fluctuates between -1 and positive 1. So, with that in mind, can we find a part of this sequence that converges to either -1 or positive 1? The answer is yes.

Since we know that once our sequence hits -1, we must go back to 1, then we can begin our subsequence where Sn = -1.
This gives us a subsequence to our main sequence:

As we can see we have a subsequence here that converges to 1, whereas our main sequence, while bounded, was not convergent.
So, a subsequence has allowed us to take a portion of our sequence and give ourselves something a little nicer to work with.
It is worth noting this can be done in a similar fashion with a subsequence which begins at 1 instead of -1.

Properties of Subsequences

So now that we know what a subsequence is, what about limits of subsequences? We have several properties for convergent sequences, such as the Monotone Convergence Theorem, Cauchy Sequences, bounded sequences etc. We also have conditions we could conclude are true from certain properties. All convergent sequences are bounded, if Sn is convergent it is Cauchy and so on.
So, with that we have our first theorem as it relates to limits of subsequences.

Bolzano-Weierstrass Theorem: Let S_n be a bounded sequence of real numbers. There thus exists a bounded subsequence 〖S_n〗_k which is convergent. So, no matter how ridiculous S_n is, if we know that it is bounded we can say that it has a bounded subsequence 〖S_n〗_k.

Example:

Consider the sequence Sn where we are successively shifting the digits of pi to the left and cutting off any remaining tens digit.
S_1=3.14159265…, S_2=1.41592653…, S_3=4.15926535…, S_4=1.59265358…, and so on.

As we can see above there is no discernable pattern to our sequence, so we can’t really say, for example, if we take all the odd n in S_n then we will have a sequence that converges to a limit L. Likewise for all the positive n in S_n.

So, what can we discern from this sequence? Well, to simplify it in a way, we are dealing in single digits, for all intents and purposes. We are shifting one digit over, then cutting off the rest. 3.1415, 1.4149…etc. So, we can safely assume that we will never shift to a number higher than 9 since we are dealing in single digits.
Therefore, we can say that our sequence is bounded by 10, since for all S_n we have S_n≤10. Now given that we have shown our main sequence to be bounded, and thus the Bolzano-Weierstrass Theorem allows us to say that S_n has some subsequence 〖S_n〗_k that is convergent even though we don’t know exactly what that subsequence is.
It is important to note that the Bolzano-Weierstrass Theorem only guarantees us one convergent subsequence. Consider the sequence (-1)^n, we know that there are two separate convergent sequences, but simply applying the theorem would only tell us that there is one.

Open Sources:

Used for defitinitions.

https://via.hypothes.is/http://matthematics.com/ura/section-subsequences.html
https://via.hypothes.is/http://matthematics.com/ura/section-bolzano.html

Used as alternative point of view.

https://digitalcommons.trinity.edu/cgi/viewcontent.cgi?article=1006&context=mono
Trench, William F., “Introduction to Real Analysis” (2013). Faculty Authored Books. 7.