Katie Rogier, Jennifer Medeiros, and Julie Mello
Definition 5.22.
Let A ⊂ R be a subset of R. Then x ∈ R is:
(1) an interior point of A if there exists δ>0 such that A ⊃ (x−δ,x+δ);
(2) an isolated point of A if x ∈ A and there exists δ>0 such that x is the only point in A that belongs to the interval (x − δ, x + δ);
(3) a boundary point of A if for every δ > 0 the interval (x − δ,x + δ) contains points in A and points not in A;
(4) an accumulation point of A if for every δ > 0 the interval (x−δ, x+δ) contains a point in A that is distinct from x.
When the set A is understood from the context, we refer, for example, to an “interior point.”
Interior and isolated points of a set belong to the set, whereas boundary and accumulation points may or may not belong to the set. In the definition of a boundary point x, we allow the possibility that x itself is a point in A belonging to (x − δ, x + δ), but in the definition of an accumulation point, we consider only points in A belonging to (x − δ, x + δ) that are distinct from x. Thus an isolated point is a boundary point, but it isn’t an accumulation point. Accumulation points are also called cluster points or limit points.
We illustrate these definitions with a number of examples.
Example 5.23.
Let I = (a, b) be an open interval and J = [a, b] a closed interval. Then the set of interior points of I or J is (a,b), and the set of boundary points consists of the two endpoints {a,b}. The set of accumulation points of I or J is the closed interval [a,b] and I, J have no isolated points. Thus, I, J have the same interior, isolated, boundary and accumulation points, but J contains its boundary points and all of its accumulation points, while I does not.
Example 5.24.
Let a < c < b and suppose that A = (a, c) ∪ (c, b)
is an open interval punctured at c. Then the set of interior points is A, the set of boundary points is {a, b, c}, the set of accumulation points is the closed interval [a, b], and there are no isolated points.
Example 5.25.
Let A=n:n∈N.
Then every point of A is an isolated point, since a sufficiently small interval about 1/n doesn’t contain 1/m for any integer m ̸= n, and A has no interior points. The set of boundary points of A is A ∪ {0}. The point 0 ∈/ A is the only accumulation point of A, since every open interval about 0 contains 1/n for sufficiently large n.
Example 5.26.
The set N of natural numbers has no interior or accumulation points. Every point of N is both a boundary point and an isolated point.
Example 5.27.
The set Q of rational numbers has no interior or isolated points, and every real number is both a boundary and accumulation point of Q.
Example 5.28.
The Cantor set C defined in Section 5.5 below has no interior points and no isolated points. The set of accumulation points and the set of boundary points of C is equal to C.
The following proposition gives a sequential definition of an accumulation point.
Proposition 5.29.
A point x ∈ R is an accumulation point of A ⊂ R if and only if there is a sequence (xn) in A with xn ̸=xforeveryn∈Nsuchthatxn →xas n → ∞.
Proof: Suppose x ∈ R is an accumulation point of A. Definition 5.22 implies that for every n ∈ N there exists xn ∈ A\{x} such that xn ∈ (x−1/n,x+1/n). It followsthatxn →xasn→∞.
Conversely, if x is the limit of a sequence (xn) in A with xn ̸= x, and U is a neighborhood of x, then xn ∈ U \ {x} for sufficiently large n ∈ N, which proves that x is an accumulation point of A.
Example 5.30.
If A=n:n∈N,
then 0 is an accumulation point of A, since (1/n) is a sequence in A such that 1/n → 0 as n → ∞. On the other hand, 1 is not an accumulation point of A since the only sequences in A that converges to 1 are the ones whose terms eventually equal 1, and the terms are required to be distinct from 1.
We can also characterize open and closed sets in terms of their interior and accumulation points.
Proposition 5.31.
A set A ⊂ R is:
(1) open if and only if every point of A is an interior point;
(2) closed if and only if every accumulation point belongs to A.
Proof. If A is open, then it is an immediate consequence of the definitions that every point in A is an interior point. Conversely, if every point x ∈ A is an interior point, then there is an open neighborhood Ux ⊂ A of x, so
A = Ux x∈A
is a union of open sets, and therefore A is open.
If A is closed and x is an accumulation point, then Proposition 5.29 and Propo- sition 5.18 imply that x ∈ A. Conversely, if every accumulation point of A belongs to A, then every x ∈ Ac has a neighborhood with no points in A, so Ac is open and A is closed.
Information taken from: https://www.math.ucdavis.edu/~hunter/intro_analysis_pdf/ch5.pdf (pgs 93-95)
Here are the definitions with a little more detail:
Let S be an arbitrary set in the real line R.
- A point b
R is called boundary point of S if every non-empty neighborhood of b intersects S and the complement of S. The set of all boundary points of S is called the boundary of S, denoted by bd(S). - A point s S is called interior point of S if there exists a neighborhood of S completely contained in S. The set of all interior points of S is called the interior, denoted by int(S).
- A point t S is called isolated point of S if there exists a neighborhood U of t such that U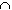
S = {t}. - A point r S is called accumulation point, if every neighborhood of r contains infinitely many distinct points of S.
Information taken from: http://www.mathcs.org/analysis/reals/topo/open.html
Exercises
Determine the set of interior points, accumulation points, isolated points, and boundary points for each of the following sets:
- (a) {1,1/2,1/3,1/4,1/5,…}
- (b) {0}∪{1,1/2,1/3,1/4,1/5,…}
(Thomas, Bruckner and Bruckner; Section 4.2, Problem 4.2.1)
Give an example of a nonempty set with no boundary points and no isolated points
or explain why you think such a set could not exist.
(Thomas, Bruckner and Bruckner; Section 4.2, Problem 4.2.2)
Let A be a set and B = R\A. Show that every boundary point of A is also a boundary point of B.
(Thomas, Bruckner and Bruckner; Section 4.2, Problem 4.2.7)
Must every boundary point of a set be also an accumulation point of that set?
(Thomas, Bruckner and Bruckner; Section 4.2, Problem 4.2.9)
Jennifer Medeiros and Julie Mello (Fall 2017)
With those definitions now, we can look at some visuals for each one.
- (1) Interior point
Our definition states that the interior of a set S is the sub set of all points of S that do not belong to the boundary of S. Any point within that interior subset is called an interior point.
Example 1:
Let S be the set of real numbers between (2, 7)
Would 3 be an interior point?
Yes 3 would be considered an interior point because it is inside of the set (2, 7)
Would 2 be an interior point?
No it would not, because one of the boundaries of the set is 2 and interior points do not include bounds.
Example 2:
Here we have a video by Joshua Helston on YouTube that explains what an interior point is from 2:13-3:12. He just draws another example with a number line in a more general form to really put together our definition of interior points.
- (2) Isolated Points
x is considered an isolated point if there exists a neighborhood of x which does not contain any other point of S. A set of isolated points is called a discrete set.
Example 3:
Using the same set from before let’s add a point. Now let’s use the set (2,7) U (9)
So now we have a single point at 9 added into our picture. The point 9 would be an isolated point because it does not contain any other point of x.
Example 4:
https://www.youtube.com/watch?v=9D-ZlJUnNZM
Here again we have another video by Joshua Helston and from the start of the video until 1:57 he talks about isolated points. Helston talks about the idea of a “deleted neighborhood.” This means that if we have a set S such that (x-δ, x+δ) the point x is not included in the set.
The neighborhood is the set (x-δ, x+δ) but, an isolated neighborhood would be (x-δ, x+δ) without the singleton {x}.
- (3) Boundary Points
The definition states if A is a subset of the reals, then a point x in the reals is a boundary point of A if every neighborhood of x contains at least one point of A and at least one point not in A.
Example 6:
If we have the set (-2, 2), call it A:
Is there a boundary point?
Yes, the red dot represents a boundary point because the point is on the border and contains both A and not A.
So in the above example a boundary point in the set A would be 2.
Are there anymore boundary points in this set A?
Yes, we can note that -2 is also a boundary point because it is on the border of A and not A.
https://www.youtube.com/watch?v=9QNI7p9T9yw
Here we have a video by Joshua Helston on YouTube that explains what a boundary point is from 3:13-4:35. In this video he explains the definition using a number line.
Example 7:
Knowing what we know now about boundary points,
If we take the set A = {(x, y) ∈ R: [latex][/latex](x^2 + y^2 < 1)[\latex]}
Does it have any boundary points?
Yes, its boundary is the circle {(x, y) ∈ R: [latex][/latex](x^2 + y^2 = 1)[\latex]} because if you look at it's graph the outside of the circle is the border of the circle which is exactly what a boundary point is. The graph shows that the points on the circle’s boundary are both part of A and not A.
Example 8:
If we take the set A = {1, 2, 3, 4, 5} as a subset of the integers, do we have a boundary point(s)?
No, there is no boundary point in this set because the entire subset in included in the set.
However if we take this same set A = {1, 2, 3, 4, 5} as a subset of the reals, we get that every element of the set is a boundary point because every element is part of A and not A.
- (4) Accumulation Points
We can note that x is an accumulation point of E, if within any distance of x, however small, there exists infinitely many points of E.
Example 9:
Let E = {1, 2} U (4, 6).
What is an example of an accumulation point? Well using our definition above we see that 5 is an accumulation point because we get (5 – c, 5 + c) ∩ E contains infinitely many points.
Is 2 an accumulation point for this same set?
No it is not because 2 is the only element in E that can be reached. If we let c = 1, then we get the set (1, 3) ∩ E = {2} which is not infinitely many solutions.
Example 10:
You may be thinking that to be an accumulation point it must be a part of the set E, but in fact this is false. You can have an accumulation point that is not in the set E.
4 is not in the set E but it is an accumulation point. 4 is an accumulation point because infinitely many solutions can be reached.
Knowing the above statement we can also say that 6 is an accumulation point that is not a part of the set E because of the same reasoning as to why 4 is an accumulation point.
With this being said we can conclude that the set E has infinitely many accumulation points within the interval [4, 6].
https://www.youtube.com/watch?v=9D-ZlJUnNZM
Here we have a video by Joshua Helston on YouTube that explains what an accumulation point is from 1:58 – 3:38. In this video he explains the definition using a number line. If you continue to watch the entire video until the end (3:39 - 5:22), he provides an example using the natural numbers.
