Macayla Sheehan
Laura Paterson
December 13, 2017
In this learning standard 3B, we will learn about real subsets that are open, closed, both, or neither.
Definition of interior point:
Let EÌR and aÎE. We say a is an interior point of E if there exists a C>0 such that (a-c, a+c)ÌE.
We write int(E) to show the set of all interior points of E.
Definition of open set:
If all points of E are interior points (so if int(E)=E), we say E is an open set.
Definition of a closed set:
A set E is called closed if the complement R \ E, is open.
Basic properties of open and closed sets:
This applies to both sets that are intersected, union together, finite, and infinite.
Adding two open sets results in an open set
Adding two closed sets results in a closed set
http://www.mathcs.org/analysis/reals/topo/open.html
- Example problem: Give an example of a collection of closed sets V1, V2, V3,… where the union V as n=1 and the union goes to infinity, Vn is N=OT closed.
Solution: V1=[1, 2] V2=[1/2, 5/2] V3=[1/3, 8/3] …. Vn=[1/n, 3-1/n].. Each of these sets are closed since each of its points are in fact accumulation points, so however, all its accumulation points are included in the set.
- An example from this collection that is NOT a closed set.
Vn=(0, 3)… This is because two of the accumulation points 0 and 3, do not belong to V. The complement of (0, 3) is (-INFINITY, 0) U [3, INFINITY), and this is not an open set since there exists a point E (0 or 3) which is NOT an interior point of E.
Sophia Nogueira
January 31, 2017
Real Analysis I
Learning Standard 3.B
Compare, contrast, and classify real subsets that are open, closed, both, or neither.
Online source 1: https://www.youtube.com/watch?v=PcnSgIoASSk
This online source was a video by Ben Garside. In the video, open and closed sets were compared visually using R2 Euclidean space on a grid. This visual showed that in an open set, we can find a point contained in the set, or an interior point, and also find a range of points that that point is contained within, for any point in the open set. This was represented by drawing circles around any arbitrarily chosen point inside the set. A closed set was then represented as the set of points that are the compliment of an open set. The closed set has boundaries.
Online source 2: http://pirate.shu.edu/~wachsmut/ira/topo/open.html
Interactive Real Analysis, ver. 1.9.5
(c) 1994-2007, Bert G. Wachsmuth
Page last modified: Mar 26, 2007
This online source discussed formal definitions of open, closed or neither sets. The source contained smaller definitions such as boundary points, interior points, isolated points, and accumulation points that helped me to understand the overarching definitions given at the top of the page. This source also gave problems and examples pertaining to the union of open sets, and the intersection of closed sets.
Four Exercises: (Dr.S note: These exercises look like they’re not relevant to our course. Measurable functions are a topic for an advanced analysis course, such as MATH 402.)
Which of the following sets are open, closed, both, or neither ?
- The intervals (-3, 3), [4, 7], (-4, 5], (0,
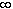) and [0, 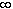) - The sets R (the whole real line) and 0 (the empty set)
- The set {1, 1/2, 1/3, 1/4, 1/5, …} and {1, 1/2, 1/3, 1/4, …}
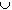{0
4. What is the boundary and the interior of (0, 4), [-1, 2], R, and O ? Which points are isolated and accumulation points, if any ?
Project part three:
My first source, YouTube allows users to mark their videos with a Creative Commons CC BY license. My second source is all rights reserved C license.
