5
Learning Objectives
- Determine the conditions for when a function has an inverse.
- Use the horizontal line test to recognize when a function is one-to-one.
- Find the inverse of a given function.
- Draw the graph of an inverse function.
- Evaluate inverse trigonometric functions.
An inverse function reverses the operation done by a particular function. In other words, whatever a function does, the inverse function undoes it. In this section, we define an inverse function formally and state the necessary conditions for an inverse function to exist. We examine how to find an inverse function and study the relationship between the graph of a function and the graph of its inverse. Then we apply these ideas to define and discuss properties of the inverse trigonometric functions.
Existence of an Inverse Function
We begin with an example. Given a function [latex]f[/latex] and an output [latex]y=f(x)[/latex], we are often interested in finding what value or values [latex]x[/latex] were mapped to [latex]y[/latex] by [latex]f[/latex]. For example, consider the function [latex]f(x)=x^3+4[/latex]. Since any output [latex]y=x^3+4[/latex], we can solve this equation for [latex]x[/latex] to find that the input is [latex]x=\sqrt[3]{y-4}[/latex]. This equation defines [latex]x[/latex] as a function of [latex]y[/latex]. Denoting this function as [latex]f^{-1}[/latex], and writing [latex]x=f^{-1}(y)=\sqrt[3]{y-4}[/latex], we see that for any [latex]x[/latex] in the domain of [latex]f, \, f^{-1}(f(x))=f^{-1}(x^3+4)=x[/latex]. Thus, this new function, [latex]f^{-1}[/latex], “undid” what the original function [latex]f[/latex] did. A function with this property is called the inverse function of the original function.
Definition
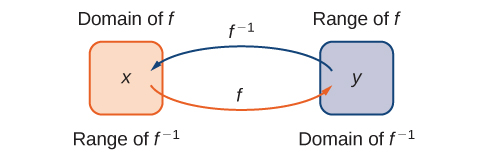
Given a function [latex]f[/latex] with domain [latex]D[/latex] and range [latex]R[/latex], its inverse function (if it exists) is the function [latex]f^{-1}[/latex] with domain [latex]R[/latex] and range [latex]D[/latex] such that [latex]f^{-1}(y)=x[/latex] if [latex]f(x)=y[/latex]. In other words, for a function [latex]f[/latex] and its inverse [latex]f^{-1}[/latex],
Note that [latex]f^{-1}[/latex] is read as “f inverse.” Here, the -1 is not used as an exponent and [latex]f^{-1}(x) \ne 1/f(x)[/latex]. (Figure) shows the relationship between the domain and range of [latex]f[/latex] and the domain and range of [latex]f^{-1}[/latex].
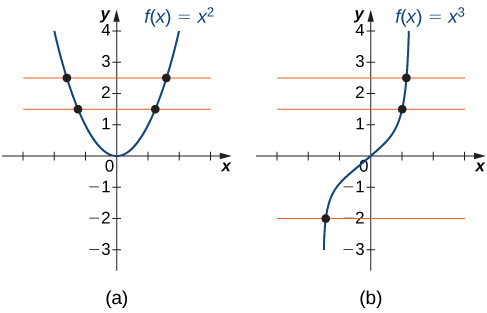
Recall that a function has exactly one output for each input. Therefore, to define an inverse function, we need to map each input to exactly one output. For example, let’s try to find the inverse function for [latex]f(x)=x^2[/latex]. Solving the equation [latex]y=x^2[/latex] for [latex]x[/latex], we arrive at the equation [latex]x= \pm \sqrt{y}[/latex]. This equation does not describe [latex]x[/latex] as a function of [latex]y[/latex] because there are two solutions to this equation for every [latex]y \symbol{"3E} 0[/latex]. The problem with trying to find an inverse function for [latex]f(x)=x^2[/latex] is that two inputs are sent to the same output for each output [latex]y \symbol{"3E} 0[/latex]. The function [latex]f(x)=x^3+4[/latex] discussed earlier did not have this problem. For that function, each input was sent to a different output. A function that sends each input to a different output is called a one-to-one function.
Definition
We say a [latex]f[/latex] is a one-to-one function if [latex]f(x_1) \ne f(x_2)[/latex] when [latex]x_1 \ne x_2[/latex].
One way to determine whether a function is one-to-one is by looking at its graph. If a function is one-to-one, then no two inputs can be sent to the same output. Therefore, if we draw a horizontal line anywhere in the [latex]xy[/latex]-plane, according to the horizontal line test , it cannot intersect the graph more than once. We note that the horizontal line test is different from the vertical line test. The vertical line test determines whether a graph is the graph of a function. The horizontal line test determines whether a function is one-to-one ( (Figure) ).
Rule: Horizontal Line Test
A function [latex]f[/latex] is one-to-one if and only if every horizontal line intersects the graph of [latex]f[/latex] no more than once.
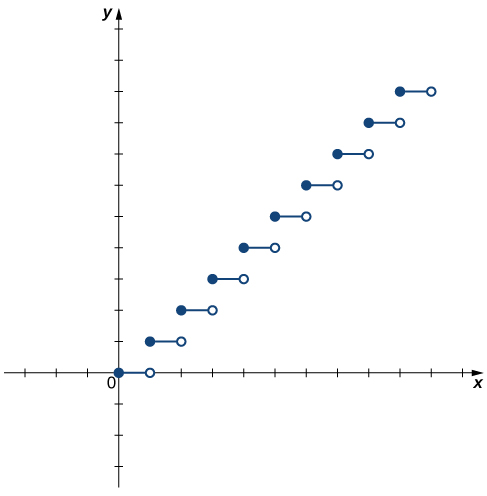
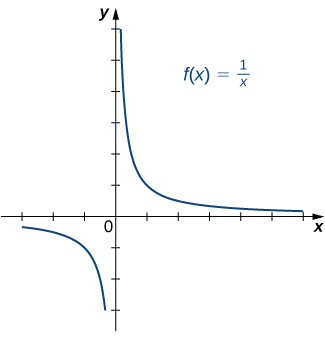
Determining Whether a Function Is One-to-One
For each of the following functions, use the horizontal line test to determine whether it is one-to-one.
Solution
- Since the horizontal line [latex]y=n[/latex] for any integer [latex]n\ge 0[/latex] intersects the graph more than once, this function is not one-to-one.

- Since every horizontal line intersects the graph once (at most), this function is one-to-one.

Is the function [latex]f[/latex] graphed in the following image one-to-one?
Hint
Use the horizontal line test.
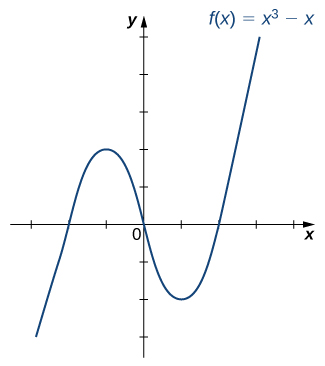
Solution
No.
Finding a Function’s Inverse
We can now consider one-to-one functions and show how to find their inverses. Recall that a function maps elements in the domain of [latex]f[/latex] to elements in the range of [latex]f[/latex]. The inverse function maps each element from the range of [latex]f[/latex] back to its corresponding element from the domain of [latex]f[/latex]. Therefore, to find the inverse function of a one-to-one function [latex]f[/latex], given any [latex]y[/latex] in the range of [latex]f[/latex], we need to determine which [latex]x[/latex] in the domain of [latex]f[/latex] satisfies [latex]f(x)=y[/latex]. Since [latex]f[/latex] is one-to-one, there is exactly one such value [latex]x[/latex]. We can find that value [latex]x[/latex] by solving the equation [latex]f(x)=y[/latex] for [latex]x[/latex]. Doing so, we are able to write [latex]x[/latex] as a function of [latex]y[/latex] where the domain of this function is the range of [latex]f[/latex] and the range of this new function is the domain of [latex]f[/latex]. Consequently, this function is the inverse of [latex]f[/latex], and we write [latex]x=f^{-1}(y)[/latex]. Since we typically use the variable [latex]x[/latex] to denote the independent variable and [latex]y[/latex] to denote the dependent variable, we often interchange the roles of [latex]x[/latex] and [latex]y[/latex], and write [latex]y=f^{-1}(x)[/latex]. Representing the inverse function in this way is also helpful later when we graph a function [latex]f[/latex] and its inverse [latex]f^{-1}[/latex] on the same axes.
Problem-Solving Strategy: Finding an Inverse Function
- Solve the equation [latex]y=f(x)[/latex] for [latex]x[/latex].
- Interchange the variables [latex]x[/latex] and [latex]y[/latex] and write [latex]y=f^{-1}(x)[/latex].
Finding an Inverse Function
Find the inverse for the function [latex]f(x)=3x-4[/latex]. State the domain and range of the inverse function. Verify that [latex]f^{-1}(f(x))=x[/latex].
Solution
Follow the steps outlined in the strategy.
Step 1. If [latex]y=3x-4[/latex], then [latex]3x=y+4[/latex] and [latex]x=\frac{1}{3}y+\frac{4}{3}[/latex].
Step 2. Rewrite as [latex]y=\frac{1}{3}x+\frac{4}{3}[/latex] and let [latex]y=f^{-1}(x)[/latex].
Therefore, [latex]f^{-1}(x)=\frac{1}{3}x+\frac{4}{3}[/latex].
Since the domain of [latex]f[/latex] is [latex](-\infty ,\infty)[/latex], the range of [latex]f^{-1}[/latex] is [latex](-\infty ,\infty)[/latex]. Since the range of [latex]f[/latex] is [latex](-\infty ,\infty)[/latex], the domain of [latex]f^{-1}[/latex] is [latex](-\infty ,\infty)[/latex].
You can verify that [latex]f^{-1}(f(x))=x[/latex] by writing
Note that for [latex]f^{-1}(x)[/latex] to be the inverse of [latex]f(x)[/latex], both [latex]f^{-1}(f(x))=x[/latex] and [latex]f(f^{-1}(x))=x[/latex] for all [latex]x[/latex] in the domain of the inside function.
Find the inverse of the function [latex]f(x)=3x/(x-2)[/latex]. State the domain and range of the inverse function.
Hint
Use the (Note) for finding inverse functions.
Solution
[latex]f^{-1}(x)=\frac{2x}{x-3}[/latex]. The domain of [latex]f^{-1}[/latex] is [latex]\{x|x \ne 3\}[/latex]. The range of [latex]f^{-1}[/latex] is [latex]\{y|y \ne 2\}[/latex].
Graphing Inverse Functions
Let’s consider the relationship between the graph of a function [latex]f[/latex] and the graph of its inverse. Consider the graph of [latex]f[/latex] shown in (Figure) and a point [latex](a,b)[/latex] on the graph. Since [latex]b=f(a)[/latex], then [latex]f^{-1}(b)=a[/latex]. Therefore, when we graph [latex]f^{-1}[/latex], the point [latex](b,a)[/latex] is on the graph. As a result, the graph of [latex]f^{-1}[/latex] is a reflection of the graph of [latex]f[/latex] about the line [latex]y=x[/latex].
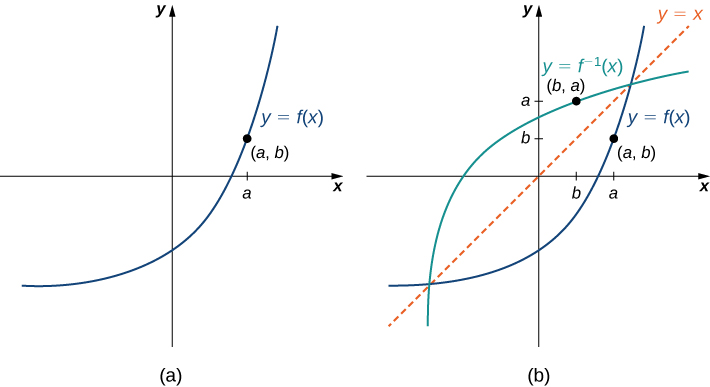
Sketching Graphs of Inverse Functions
For the graph of [latex]f[/latex] in the following image, sketch a graph of [latex]f^{-1}[/latex] by sketching the line [latex]y=x[/latex] and using symmetry. Identify the domain and range of [latex]f^{-1}[/latex].
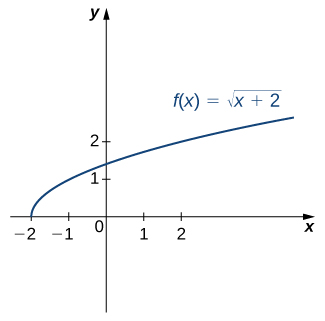
Solution
Reflect the graph about the line [latex]y=x[/latex]. The domain of [latex]f^{-1}[/latex] is [latex][0,\infty)[/latex]. The range of [latex]f^{-1}[/latex] is [latex][-2,\infty)[/latex]. By using the preceding strategy for finding inverse functions, we can verify that the inverse function is [latex]f^{-1}(x)=x^2-2[/latex], as shown in the graph.

Sketch the graph of [latex]f(x)=2x+3[/latex] and the graph of its inverse using the symmetry property of inverse functions.
Hint
The graphs are symmetric about the line [latex]y=x[/latex].
Solution

Restricting Domains
As we have seen, [latex]f(x)=x^2[/latex] does not have an inverse function because it is not one-to-one. However, we can choose a subset of the domain of [latex]f[/latex] such that the function is one-to-one. This subset is called a restricted domain. By restricting the domain of [latex]f[/latex], we can define a new function [latex]g[/latex] such that the domain of [latex]g[/latex] is the restricted domain of [latex]f[/latex] and [latex]g(x)=f(x)[/latex] for all [latex]x[/latex] in the domain of [latex]g[/latex]. Then we can define an inverse function for [latex]g[/latex] on that domain. For example, since [latex]f(x)=x^2[/latex] is one-to-one on the interval [latex][0,\infty)[/latex], we can define a new function [latex]g[/latex] such that the domain of [latex]g[/latex] is [latex][0,\infty)[/latex] and [latex]g(x)=x^2[/latex] for all [latex]x[/latex] in its domain. Since [latex]g[/latex] is a one-to-one function, it has an inverse function, given by the formula [latex]g^{-1}(x)=\sqrt{x}[/latex]. On the other hand, the function [latex]f(x)=x^2[/latex] is also one-to-one on the domain [latex](-\infty,0][/latex]. Therefore, we could also define a new function [latex]h[/latex] such that the domain of [latex]h[/latex] is [latex](-\infty,0][/latex] and [latex]h(x)=x^2[/latex] for all [latex]x[/latex] in the domain of [latex]h[/latex]. Then [latex]h[/latex] is a one-to-one function and must also have an inverse. Its inverse is given by the formula [latex]h^{-1}(x)=-\sqrt{x}[/latex] ( (Figure) ).
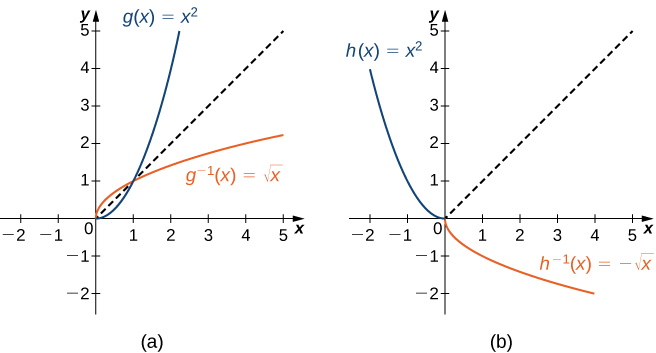
Restricting the Domain
Consider the function [latex]f(x)=(x+1)^2[/latex].
- Sketch the graph of [latex]f[/latex] and use the horizontal line test to show that [latex]f[/latex] is not one-to-one.
- Show that [latex]f[/latex] is one-to-one on the restricted domain [latex][-1,\infty)[/latex]. Determine the domain and range for the inverse of [latex]f[/latex] on this restricted domain and find a formula for [latex]f^{-1}[/latex].
Solution
- The graph of [latex]f[/latex] is the graph of [latex]y=x^2[/latex] shifted left 1 unit. Since there exists a horizontal line intersecting the graph more than once, [latex]f[/latex] is not one-to-one.

- On the interval [latex][-1,\infty), \, f[/latex] is one-to-one.

The domain and range of [latex]f^{-1}[/latex] are given by the range and domain of [latex]f[/latex], respectively. Therefore, the domain of [latex]f^{-1}[/latex] is [latex][0,\infty)[/latex] and the range of [latex]f^{-1}[/latex] is [latex][-1,\infty)[/latex]. To find a formula for [latex]f^{-1}[/latex], solve the equation [latex]y=(x+1)^2[/latex] for [latex]x[/latex]. If [latex]y=(x+1)^2[/latex], then [latex]x=-1 \pm \sqrt{y}[/latex]. Since we are restricting the domain to the interval where [latex]x \ge -1[/latex], we need [latex]\pm \sqrt{y} \ge 0[/latex]. Therefore, [latex]x=-1+\sqrt{y}[/latex]. Interchanging [latex]x[/latex] and [latex]y[/latex], we write [latex]y=-1+\sqrt{x}[/latex] and conclude that [latex]f^{-1}(x)=-1+\sqrt{x}[/latex].
Consider [latex]f(x)=1/x^2[/latex] restricted to the domain [latex](-\infty ,0)[/latex]. Verify that [latex]f[/latex] is one-to-one on this domain. Determine the domain and range of the inverse of [latex]f[/latex] and find a formula for [latex]f^{-1}[/latex].
Hint
The domain and range of [latex]f^{-1}[/latex] is given by the range and domain of [latex]f[/latex], respectively. To find [latex]f^{-1}[/latex], solve [latex]y=1/x^2[/latex] for [latex]x[/latex].
Solution
The domain of [latex]f^{-1}[/latex] is [latex](0,\infty)[/latex]. The range of [latex]f^{-1}[/latex] is [latex](-\infty ,0)[/latex]. The inverse function is given by the formula [latex]f^{-1}(x)=-1/\sqrt{x}[/latex].
Inverse Trigonometric Functions
The six basic trigonometric functions are periodic, and therefore they are not one-to-one. However, if we restrict the domain of a trigonometric function to an interval where it is one-to-one, we can define its inverse. Consider the sine function ( (Figure) ). The sine function is one-to-one on an infinite number of intervals, but the standard convention is to restrict the domain to the interval [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]. By doing so, we define the inverse sine function on the domain [latex][-1,1][/latex] such that for any [latex]x[/latex] in the interval [latex][-1,1][/latex], the inverse sine function tells us which angle [latex]\theta[/latex] in the interval [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex] satisfies [latex]\sin \theta =x[/latex]. Similarly, we can restrict the domains of the other trigonometric functions to define i nverse trigonometric functions , which are functions that tell us which angle in a certain interval has a specified trigonometric value.
Definition
The inverse sine function, denoted [latex]\sin^{-1}[/latex] or arcsin, and the inverse cosine function, denoted [latex]\cos^{-1}[/latex] or arccos, are defined on the domain [latex]D=\{x|-1 \le x \le 1\}[/latex] as follows:
The inverse tangent function, denoted [latex]\tan^{-1}[/latex] or arctan, and inverse cotangent function, denoted [latex]\cot^{-1}[/latex] or arccot, are defined on the domain [latex]D=\{x|-\infty The inverse cosecant function, denoted [latex]\csc^{-1}[/latex] or arccsc, and inverse secant function, denoted [latex]\sec^{-1}[/latex] or arcsec, are defined on the domain [latex]D=\{x| \, |x| \ge 1\}[/latex] as follows: To graph the inverse trigonometric functions, we use the graphs of the trigonometric functions restricted to the domains defined earlier and reflect the graphs about the line [latex]y=x[/latex] ( (Figure) ). Go to the following site for more comparisons of functions and their inverses. When evaluating an inverse trigonometric function, the output is an angle. For example, to evaluate [latex]\cos^{-1}(\frac{1}{2})[/latex], we need to find an angle [latex]\theta[/latex] such that [latex]\cos \theta =\frac{1}{2}[/latex]. Clearly, many angles have this property. However, given the definition of [latex]\cos^{-1}[/latex], we need the angle [latex]\theta[/latex] that not only solves this equation, but also lies in the interval [latex][0,\pi][/latex]. We conclude that [latex]\cos^{-1}(\frac{1}{2})=\frac{\pi}{3}[/latex]. We now consider a composition of a trigonometric function and its inverse. For example, consider the two expressions [latex]\sin (\sin^{-1}(\frac{\sqrt{2}}{2}))[/latex] and [latex]\sin^{-1}(\sin(\pi))[/latex]. For the first one, we simplify as follows: For the second one, we have The inverse function is supposed to “undo” the original function, so why isn’t [latex]\sin^{-1}(\sin (\pi))=\pi[/latex]? Recalling our definition of inverse functions, a function [latex]f[/latex] and its inverse [latex]f^{-1}[/latex] satisfy the conditions [latex]f(f^{-1}(y))=y[/latex] for all [latex]y[/latex] in the domain of [latex]f^{-1}[/latex] and [latex]f^{-1}(f(x))=x[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex], so what happened here? The issue is that the inverse sine function, [latex]\sin^{-1}[/latex], is the inverse of the restricted sine function defined on the domain [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]. Therefore, for [latex]x[/latex] in the interval [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex], it is true that [latex]\sin^{-1}(\sin x)=x[/latex]. However, for values of [latex]x[/latex] outside this interval, the equation does not hold, even though [latex]\sin^{-1}(\sin x)[/latex] is defined for all real numbers [latex]x[/latex]. What about [latex]\sin (\sin^{-1}y)[/latex]? Does that have a similar issue? The answer is no . Since the domain of [latex]\sin^{-1}[/latex] is the interval [latex][-1,1][/latex], we conclude that [latex]\sin (\sin^{-1}y)=y[/latex] if [latex]-1 \le y \le 1[/latex] and the expression is not defined for other values of [latex]y[/latex]. To summarize, and Similarly, for the cosine function, and Similar properties hold for the other trigonometric functions and their inverses. Evaluate each of the following expressions. In many areas of science, engineering, and mathematics, it is useful to know the maximum value a function can obtain, even if we don’t know its exact value at a given instant. For instance, if we have a function describing the strength of a roof beam, we would want to know the maximum weight the beam can support without breaking. If we have a function that describes the speed of a train, we would want to know its maximum speed before it jumps off the rails. Safe design often depends on knowing maximum values. This project describes a simple example of a function with a maximum value that depends on two equation coefficients. We will see that maximum values can depend on several factors other than the independent variable [latex]x[/latex]. Using a graphing calculator or other graphing device, estimate the [latex]x[/latex]– and [latex]y[/latex]-values of the maximum point for the graph (the first such point where [latex]x \symbol{"3E} 0[/latex]). It may be helpful to express the [latex]x[/latex]-value as a multiple of [latex]\pi[/latex].
Evaluating Expressions Involving Inverse Trigonometric Functions
Solution
The Maximum Value of a Function

[latex]A[/latex]
[latex]B[/latex]
[latex]x[/latex]
[latex]y[/latex]
[latex]A[/latex]
[latex]B[/latex]
[latex]x[/latex]
[latex]y[/latex]
0
1
[latex]\sqrt{3}[/latex]
1
1
0
1
[latex]\sqrt{3}[/latex]
1
1
12
5
1
2
5
12
2
1
2
2
3
4
4
3
Key Concepts
- For a function to have an inverse, the function must be one-to-one. Given the graph of a function, we can determine whether the function is one-to-one by using the horizontal line test.
- If a function is not one-to-one, we can restrict the domain to a smaller domain where the function is one-to-one and then define the inverse of the function on the smaller domain.
- For a function [latex]f[/latex] and its inverse [latex]f^{-1}, \, f(f^{-1}(x))=x[/latex] for all [latex]x[/latex] in the domain of [latex]f^{-1}[/latex] and [latex]f^{-1}(f(x))=x[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex].
- Since the trigonometric functions are periodic, we need to restrict their domains to define the inverse trigonometric functions.
- The graph of a function [latex]f[/latex] and its inverse [latex]f^{-1}[/latex] are symmetric about the line [latex]y=x[/latex].
Key Equations
- Inverse functions
[latex]f^{-1}(f(x))=x[/latex] for all [latex]x[/latex] in [latex]D[/latex], and [latex]f(f^{-1}(y))=y[/latex] for all [latex]y[/latex] in [latex]R[/latex].[/latex]
For the following exercises, use the horizontal line test to determine whether each of the given graphs is one-to-one.
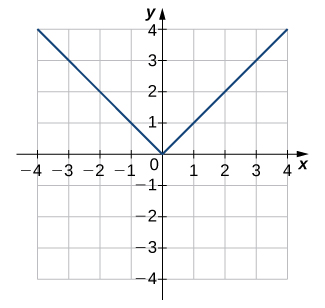
Solution
Not one-to-one
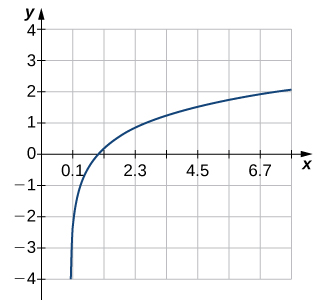
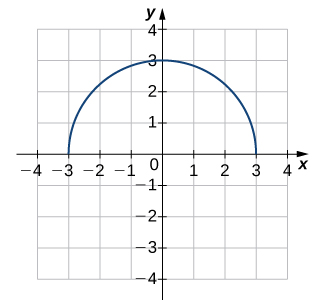
Solution
Not one-to-one
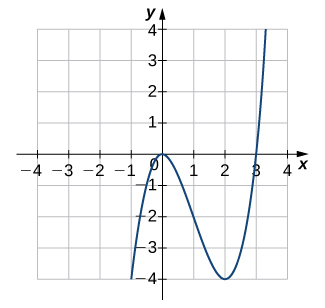
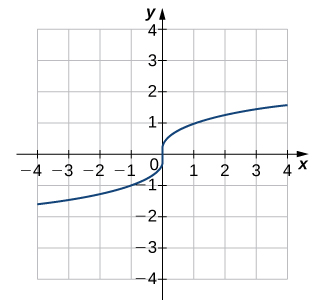
Solution
One-to-one
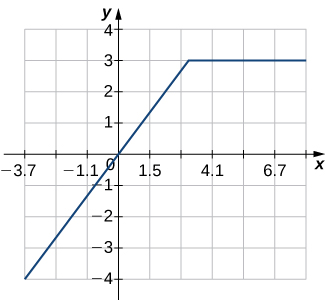
For the following exercises, a. find the inverse function, and b. find the domain and range of the inverse function.
7. [latex]f(x)=x^2-4, \, x \ge 0[/latex]
Solution
a. [latex]f^{-1}(x)=\sqrt{x+4}[/latex] b. Domain: [latex][-4,\infty)[/latex], Range: [latex][0,\infty)[/latex]
8. [latex]f(x)=\sqrt[3]{x-4}[/latex]
9. [latex]f(x)=x^3+1[/latex]
Solution
a. [latex]f^{-1}(x)=\sqrt[3]{x-1}[/latex] b. Domain: all real numbers, Range: all real numbers
10. [latex]f(x)=(x-1)^2, \, x \le 1[/latex]
11. [latex]f(x)=\sqrt{x-1}[/latex]
Solution
a. [latex]f^{-1}(x)=x^2+1[/latex], b. Domain: [latex][0,\infty)[/latex], Range: [latex][1,\infty)[/latex]
12. [latex]f(x)=\frac{1}{x+2}[/latex]
13. [latex]f(x)=\frac{4x-1}{2x+3}[/latex]
Solution
a. [latex]f^{-1}(x)=\frac{-1-3x}{2(x-2)}[/latex], b. Domain: [latex](-\infty,2) \cup (2,\infty)[/latex], Range: [latex](-\infty, -\frac{3}{2}) \cup (-\frac{3}{2},\infty)[/latex]
14. [latex]f(x)=\frac{1-2x}{5+x}[/latex]
For the following exercises, use the graph of [latex]f[/latex] to sketch the graph of its inverse function.
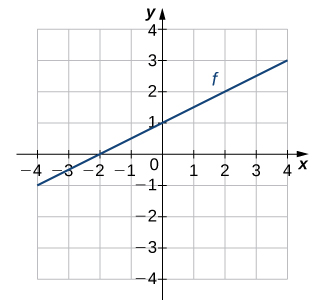
Solution

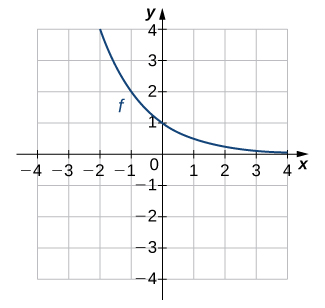
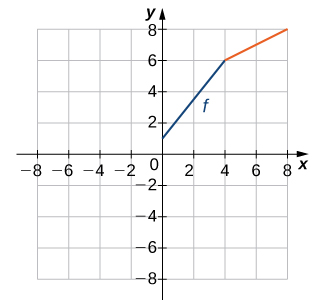
Solution

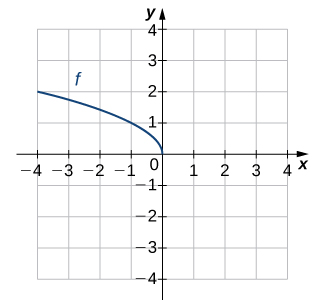
For the following exercises, use composition to determine which pairs of functions are inverses.
19. [latex]f(x)=8x, \, g(x)=\frac{x}{8}[/latex]
Solution
These are inverses.
20. [latex]f(x)=8x+3, \, g(x)=\frac{x-3}{8}[/latex]
21. [latex]f(x)=5x-7, \, g(x)=\frac{x+5}{7}[/latex]
Solution
These are not inverses.
22. [latex]f(x)=\frac{2}{3}x+2, \, g(x)=\frac{3}{2}x+3[/latex]
23. [latex]f(x)=\frac{1}{x-1}, \, x \ne 1, \, g(x)=\frac{1}{x}+1, \, x \ne 0[/latex]
Solution
These are inverses.
24. [latex]f(x)=x^3+1, \, g(x)=(x-1)^{1/3}[/latex]
25. [latex]f(x)=x^2+2x+1, \, x \ge -1,\, g(x)=-1+\sqrt{x}, \, x \ge 0[/latex]
Solution
These are inverses.
26. [latex]f(x)=\sqrt{4-x^2}, \, 0 \le x \le 2, \, g(x)=\sqrt{4-x^2}, \, 0 \le x \le 2[/latex]
For the following exercises, evaluate the functions. Give the exact value.
27. [latex]\tan^{-1}(\frac{\sqrt{3}}{3})[/latex]
Solution
[latex]\frac{\pi}{6}[/latex]
28. [latex]\cos^{-1}(-\frac{\sqrt{2}}{2})[/latex]
29. [latex]\cot^{-1}(1)[/latex]
Solution
[latex]\frac{\pi}{4}[/latex]
30. [latex]\sin^{-1}(-1)[/latex]
31. [latex]\cos^{-1}(\frac{\sqrt{3}}{2})[/latex]
Solution
[latex]\frac{\pi}{6}[/latex]
32. [latex]\cos (\tan^{-1}(\sqrt{3}))[/latex]
33. [latex]\sin (\cos^{-1}(\frac{\sqrt{2}}{2}))[/latex]
34. [latex]\sin^{-1}( \sin (\frac{\pi}{3}))[/latex]
35. [latex]\tan^{-1}( \tan (-\frac{\pi}{6}))[/latex]
Solution
[latex]-\frac{\pi}{6}[/latex]
36. The function [latex]C=T(F)=(5/9)(F-32)[/latex] converts degrees Fahrenheit to degrees Celsius.
- Find the inverse function [latex]F=T^{-1}(C)[/latex]
- What is the inverse function used for?
37. [T] The velocity [latex]V[/latex] (in centimeters per second) of blood in an artery at a distance [latex]x[/latex] cm from the center of the artery can be modeled by the function [latex]V=f(x)=500(0.04-x^2)[/latex] for [latex]0 \le x \le 0.2[/latex].
- Find [latex]x=f^{-1}(V)[/latex].
- Interpret what the inverse function is used for.
- Find the distance from the center of an artery with a velocity of 15 cm/sec, 10 cm/sec, and 5 cm/sec.
Solution
a. [latex]x=f^{-1}(V)=\sqrt{0.04-\frac{V}{500}}[/latex] b. The inverse function determines the distance from the center of the artery at which blood is flowing with velocity [latex]V[/latex]. c. 0.1 cm; 0.14 cm; 0.17 cm
38. A function that converts dress sizes in the United States to those in Europe is given by [latex]D(x)=2x+24[/latex].
- Find the European dress sizes that correspond to sizes 6, 8, 10, and 12 in the United States.
- Find the function that converts European dress sizes to U.S. dress sizes.
- Use part b. to find the dress sizes in the United States that correspond to 46, 52, 62, and 70.
39. [T] The cost to remove a toxin from a lake is modeled by the function
[latex]C(p)=75p/(85-p)[/latex], where [latex]C[/latex] is the cost (in thousands of dollars) and [latex]p[/latex] is the amount of toxin in a small lake (measured in parts per billion [ppb]). This model is valid only when the amount of toxin is less than 85 ppb.
- Find the cost to remove 25 ppb, 40 ppb, and 50 ppb of the toxin from the lake.
- Find the inverse function. c. Use part b. to determine how much of the toxin is removed for $50,000.
Solution
a. $31,250, $66,667, $107,143 b. [latex](p=\frac{85C}{C+75})[/latex] c. 34 ppb
40. [T] A race car is accelerating at a velocity given by
[latex]v(t)=\frac{25}{4}t+54[/latex],
where [latex]v[/latex] is the velocity (in feet per second) at time [latex]t[/latex].
- Find the velocity of the car at 10 sec.
- Find the inverse function.
- Use part b. to determine how long it takes for the car to reach a speed of 150 ft/sec.
41. [T] An airplane’s Mach number [latex]M[/latex] is the ratio of its speed to the speed of sound. When a plane is flying at a constant altitude, then its Mach angle is given by [latex]\mu =2\sin^{-1}(\frac{1}{M})[/latex].
Find the Mach angle (to the nearest degree) for the following Mach numbers.
 1.0”.
1.0”.
- [latex]\mu =1.4[/latex]
- [latex]\mu =2.8[/latex]
- [latex]\mu =4.3[/latex]
Solution
a. [latex]~92^{\circ}[/latex] b. [latex]~42^{\circ}[/latex] c. [latex]~27^{\circ}[/latex]
42. [T] Using [latex]\mu =2\sin^{-1}(\frac{1}{M})[/latex], find the Mach number [latex]M[/latex] for the following angles.
- [latex]\mu =\frac{\pi}{6}[/latex]
- [latex]\mu =\frac{2\pi}{7}[/latex]
- [latex]\mu =\frac{3\pi}{8}[/latex]
43. [T] The temperature (in degrees Celsius) of a city in the northern United States can be modeled by the function
[latex]T(x)=5+18 \sin[\frac{\pi}{6}(x-4.6)][/latex],
where [latex]x[/latex] is time in months and [latex]x=1.00[/latex] corresponds to January 1. Determine the month and day when the temperature is [latex]21^{\circ}[/latex] C.
Solution
[latex]x \approx 6.69,8.51[/latex]; so, the temperature occurs on June 21 and August 15
44. [T] The depth (in feet) of water at a dock changes with the rise and fall of tides. It is modeled by the function
[latex]D(t)=5 \sin (\frac{\pi}{6}t-\frac{7\pi}{6})+8[/latex],
where [latex]t[/latex] is the number of hours after midnight. Determine the first time after midnight when the depth is 11.75 ft.
45. [T] An object moving in simple harmonic motion is modeled by the function
[latex]s(t)=-6 \cos (\frac{\pi t}{2})[/latex],
where [latex]s[/latex] is measured in inches and [latex]t[/latex] is measured in seconds. Determine the first time when the distance moved is 4.5 in.
Solution
[latex]~1.5 \sec[/latex]
46. [T] A local art gallery has a portrait 3 ft in height that is hung 2.5 ft above the eye level of an average person. The viewing angle [latex]\theta[/latex] can be modeled by the function
[latex]\theta =\tan^{-1}\frac{5.5}{x}-\tan^{-1}\frac{2.5}{x}[/latex],
where [latex]x[/latex] is the distance (in feet) from the portrait. Find the viewing angle when a person is 4 ft from the portrait.
47. [T] Use a calculator to evaluate [latex]\tan^{-1}( \tan (2.1))[/latex] and [latex]\cos^{-1}( \cos (2.1))[/latex]. Explain the results of each.
Solution
[latex]\tan^{-1}( \tan (2.1))\approx -1.0416[/latex]; the expression does not equal 2.1 since [latex]2.1 \symbol{"3E} 1.57=\frac{\pi}{2}[/latex]—in other words, it is not in the restricted domain of [latex]\tan x[/latex]. [latex]\cos^{-1}( \cos (2.1))=2.1[/latex], since 2.1 is in the restricted domain of [latex]\cos x[/latex].
48. [T] Use a calculator to evaluate [latex]\sin (\sin^{-1}(-2))[/latex] and [latex]\tan (\tan^{-1}(-2))[/latex]. Explain the results of each.
Glossary
- horizontal line test
- a function [latex]f[/latex] is one-to-one if and only if every horizontal line intersects the graph of [latex]f[/latex], at most, once
- inverse function
- for a function [latex]f[/latex], the inverse function [latex]f^{-1}[/latex] satisfies [latex]f^{-1}(y)=x[/latex] if [latex]f(x)=y[/latex]
- inverse trigonometric functions
- the inverses of the trigonometric functions are defined on restricted domains where they are one-to-one functions
- one-to-one function
- a function [latex]f[/latex] is one-to-one if [latex]f(x_1) \ne f(x_2)[/latex] if [latex]x_1 \ne x_2[/latex]
- restricted domain
- a subset of the domain of a function [latex]f[/latex]