1.1 Why do we model systems?

Modeling allows one to analyze a system without actually constructing the physical system. It is not always ideal to analyze a physical system for various reasons, such as expense. Using differential equations, we are able to represent dynamic systems in mathematical terms in order to gain insight to its dynamic behavior.

For example, in mechanical systems, one can build such equations from the equations of motion:sum F equals m times a, where F are the forces applied to the body, m is the mass of the body and a is the acceleration of the body with respect to the inertial frame, and sigma M equals I times alpha, where M are the moments applied about the center of mass of the body, I is the body’s moment of inertia, and α is the angular acceleration of the body.  Similarly, one can use Kirchoff’s laws to build dynamic system equations for electrical systems.

In this chapter and the next, we will examine two mathematical representations of dynamic systems: the state-space representation and the transfer function.  In Chapter 3, we will then build the mathematical model of the dynamic behavior of mechanical, electrical, thermal, and fluid systems in these two forms.

1.2 State-Space Representation of Differential Equations

In control systems, state-space representation is a representation of a dynamic system that is achieved by breaking down high-order differential equations into multiple first-order differential equations.

The following terminology is important for understanding state-space representation:

State is the smallest set of variables (n) such that knowledge of the value of these variables at a given time (to) and knowledge of any system input determines the dynamic behavior of the system.

State variables are the variables making up the smallest set of variables determining the state of a system (x1, x2, x3,…xn).

A state vector is a vector of the state variables ( x ).

State-space is the n-dimensional space where the axes are the state variables.  Any state can be represented as a point in this space.

State-space equations are a set of equations modeling a dynamic system in state-space.  In general these equations take the form:

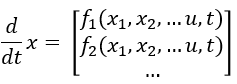
the derivative of x with respect to t equals multiple functions with input arguments such as x1, x2, u and t

To form the state-space representation, it is first important to obtain all the differential equations that describe the system.  In Chapter 3, we will discuss how these may be derived.  Once you have the differential equations that describe the dynamics of a system, the following steps can be used to create the state-space equations:

  1. Solve each differential equation for the highest derivative.
  2. If the highest derivative of an equation is greater than one, you will want to have another state variable for each order above one (so two state variables for a second-order differential equation for example).  Create another differential equation for each order of the highest derivative.  These equations should simply equate the derivative of one state variable to another state variable.
  3. Use these equations to create the state-space equations.

Example 1.1: From Differential Equation to State-Space Representation

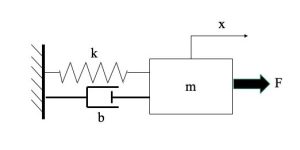In this example, there is a mass-damper-spring system. There is an external force applied to the system, notated as F in the diagram. The spring and damper are assumed to behave linearly, friction is negligible, and mass is a point.

First, we must determine the differential equations that adequately describe the model. By applying sigma F equals m times a, we determine that the external force applied is acting in the positive x-direction, while the spring and damper forces are acting in the negative x-direction, which is towards the wall.

The result is a second-order differential equation:negative b times x dot minus k times x plus F equals m times a equals m times x double dot

Recall that x indicates position, x dotindicates velocity and x double dot indicates acceleration.

We will assign x, which is position, to variable x1 and x dot, which is velocity, to variable x2:

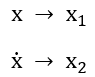
Next, we will take the derivative of x1  and x2:

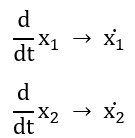
Finally, we know that the resulting x one dot is velocity, which is equivalent to x2, and resulting x two dot is acceleration, which is equal to the rearranged second-order differential equation we found for the system:

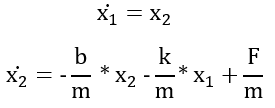
x one dot equals x two and x two dot equals negative b over m time x two minus k over m times x one plus F over m

Writing this in matrix form becomes:

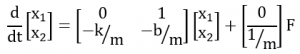
This is State-Space Representation.

Example 1.2: Inverted Pendulum

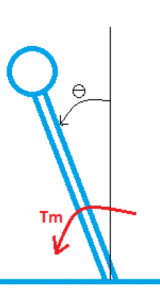
Figure 1.1: Inverted Pendulum with applied torque

Below is the differential equation representing the motion of an inverted pendulum with an applied torque:

Equation 1.1

 

 

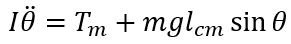
In Figure 1.1 of the inverted pendulum, Tm represents the applied torque. This system is not translating due to being fixed on one end. By applying sum of the moments applied about the center of mass of a body equals the bodys mass moment of inertial about its center of mass multiplied by the angular acceleration of the body, we can derive Equation 1.1. In addition to the applied torque, we have the moment created by the perpendicular force and the length of the string. Our state-space variables are θ and theta dot. Our state-space is 2-dimensional and the resulting state-space equations are:

State-Space Equations for an Inverted Pendulum with applied torque

 

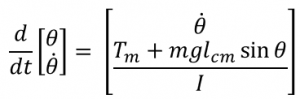
To solve the resulting differential equations, we need to know the initial conditions, and what input signals are being introduced to the system, which in this case would be Tm.

1.3 Solving State-Space Equations Numerically

With the state-space formatted differential equation,  initial conditions of the state variables, and any input signals to the system, it is possible solve for the dynamics of the state variables with time.

Using Ordinary Differential Equation (ODE) Solvers, such as Runge-Kutta Methods, we can also use ODE Solvers through MATLAB. Information on ODE Solvers in MATLAB is available online.

Matlab Example 1.1

To implement a state space equation, we could use an ordinary differential equation (ODE) solver. These solvers use a numerical method to integrate the state space equations over time. To use Matlab’s ODE solvers, one first has to create a function representing the state-space equation. In this example, we will use the equation of a damped inverted pendulum.

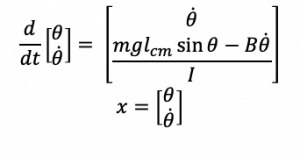
%% This function is the state-space representation
% of an inverted pendulum
function xdot = pendulum(t, x)
% input variables: t for time,
%                         x is an array of the state variables:
%                                      angle and angular velocity
xdot = x; % setting xdot is the same shape and size as x
%setting some constants
g = 9.8;
lcm = 1;
m = 1;
I = 1;
B = 1;

%State space equations. These equations return an array
% xdot that is the derivative of angle and angular velocity
xdot(1) = x(2); %dtheta/dt = theta_dot
xdot(2) = (m*g*lcm*sin(x(1))-B*x(2))/I;

end

In a separate file, we create a script that calls the ODE solver. The function ode45 is one of a selection of ordinary differential equations solver functions available in Matlab. The input to this function is the name of the function housing our state-space equations as a text string, an array containing the start and stop times, and an array containing the initial conditions of the state variables. Here we plot the resulting values of the angle (θ, the first column of the state variable data returned by the function x(:,1)) as a function of time.
theta_0 = 0.2;
theta_dot_0 = 0;
[t,x] = ode45(‘pendulum’, [0 10], [theta_0 theta_dot_0]);
plot(t,x(:,1))
xlabel(‘Time (s)’)
ylabel(‘Angle (radians)’)

We can also examine the data in a phase plane plot, where we examine the plot of one state variable against another, in this example the angle (x(:,1)) versus the angular velocity (x(:,2)).
plot(x(:,1),x(:,2))
xlabel(‘Angle (radians)’)
ylabel(‘Angular Velocity (radians/sec)’)

Finally, we can examine the system dynamics for an array of initial conditions.
for th_0 = -6:1:6
  for th_dot_0 = -6:1:6
    [t,x] = ode45(‘pendulum’, [0 10], [th_0 th_dot_0]);
    plot(x(:,1),x(:,2))
    xlabel(‘Angle (radians)’)
    ylabel(‘Angular Velocity (radians/sec)’)
    hold on
  end
end

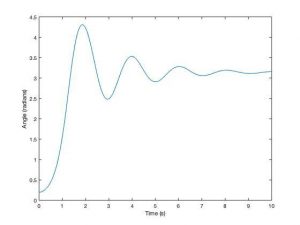
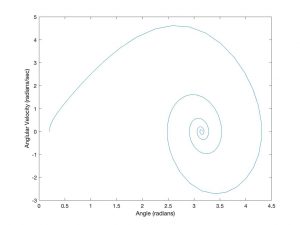
We can also build these operations in one file using the @ to designate the function and adding the function to the end of the same file.

%% Call Ode Solver for the pendulum dynamic equations
th_0 = 0.2;
th_dot_0 = 0;
[t,x] = ode45(@pendulum_damped, [0 10], [th_0 th_dot_0]);

figure(1)
plot(t,x(:,1))
xlabel(‘Time (s)’)
ylabel(‘Angle (radians)’)

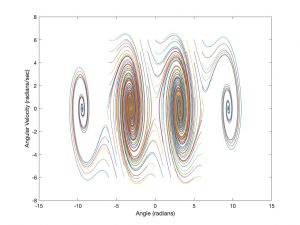
%% Phase plane plot
figure(2)
plot(x(:,1),x(:,2))
xlabel(‘Angle (radians)’)
ylabel(‘Anglular Velocity (radians/sec)’)

%% Call Ode Solver for the pendulum dynamic
% equations for several initial conditions

for th_0 = -6:1:6
for th_dot_0 = -6:1:6
[t,x] = ode45(@pendulum_damped, [0 10], [th_0 th_dot_0]);
figure(3)
plot(x(:,1),x(:,2))
xlabel(‘Angle (radians)’)
ylabel(‘Angular Velocity (radians/sec)’)
hold on
    end
end

%%  This function is the state-space representation
% of an inverted pendulum

function xdot = pendulum_damped(t, x)

% input variables: t for time,
%             x is an array of the state variables:
%                               angle and angular velocity

xdot = x;  % just making sure xdot is the same shape and size as x

%setting some constants
g = 9.8;
lcm = 1;
m = 1;
I = 1;
B = 1;

% State space equations.  These equations return
% an array xdot that is the derivative of angle and
% angular velocity

xdot(1) = x(2);  %dth/dt = th_dot
xdot(2) = (m*g*lcm*sin(x(1))-B*x(2))/I;

end

 

 

1.4 Linearization

Through the process of Linearization, a nonlinear model is represented as a linear model through use of linear approximation.

Taylor Series Expansion

In order to perform Linearization, the first two terms of the Taylor Series Expansion can be used.

Taylor Series Expansion

 

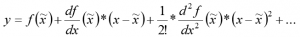
where f of x tilde is the nonlinear equation, x tilde is the equilibrium point, and x is the state variable of the system

 

The resulting y equation is the linear approximation for the nonlinear equation. The following example will detail the linearization process using Taylor Series Expansion.

Example 1.5 Linearization of sin(θ)

Problem Statement: linearize y=sin(θ) at theta tilde equals zero

 

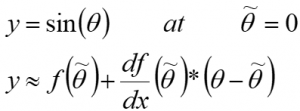
These are the first two terms of the Taylor Series Expansion

 

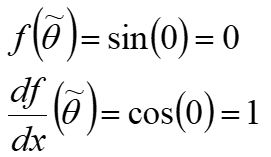
For the first term, we are able to plug in the value of theta tilde into our nonlinear equation.

For the second term, we take the derivative of the nonlinear equation and plug in theta tilde into this equation.

 

Lastly, we sum the first and second term.

The result is the linear approximation of the nonlinear equation.

 

The following example is a continuation of Example 1.2 Inverted Pendulum with applied linearization.

Example 1.6: Linearizing an Inverted Pendulum with Applied Torque

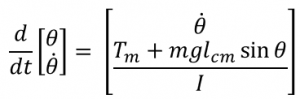
Recall from Example 1.2, we have the resulting state-space equations shown above. If we linearize and assume that sinθ=θ then the equations become:

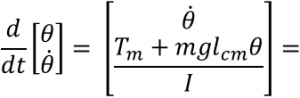
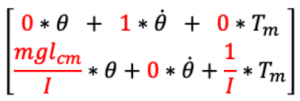
Notice that the syntax of our state-space equations varies from the syntax of the equations we found at the end of Example 1.2.

Why can we express our equations in this syntax?

Recall that state-space equations take the form

 

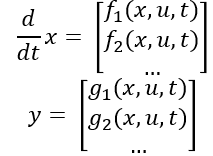
with the state variables vector expressed as x, the input variables vector is expressed as u and the output variables vector is expressed as y.

 

 

If the equations are linear, you can arrange the variables in the following way:

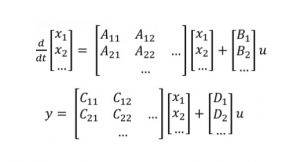
As long as these equations are linear and time invariant, A, B, C and D are matrices of constants.

 

Example 1.7: Cruise Control

Problem Statement: Determine the state-space equations for the cart in the figure.

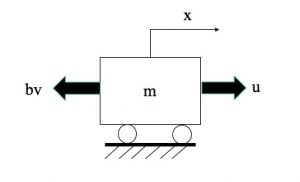
Cruise control is used in cars to maintain a certain speed despite disturbances such as changes in road conditions, elevation or resistance.

In this diagram, u represents the force exerted by the vehicle to advance forward and maintain the desired speed, and bv represents the resistive forces acting against u, such as wind resistance and friction between the tires and the road. The car’s position is x and its velocity is v.

In this problem, the variables are x, v, and u. The constants are b and m, with b representing a damping coefficient and m representing the mass of the car. The state is 2-dimensional.

Usingsigma f vector equals mass times acceleration vector, we can determine that the system equation is m times v dot equals negative b times velocity plus u. The state-space variables are x and v. The resulting state-space equations are:

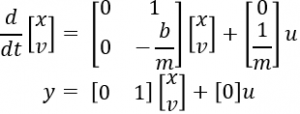
The resulting y equation above reflects our interest in controlling the speed of the car, so therefore we are interested in the velocity of the car.

 

Exercises

Exercise 1.1

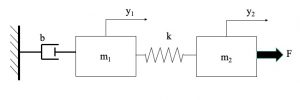
Determine the differential equations that adequately models this system. List your assumptions. Then, represent the system in State-Space representation.

 

 

Exercise 1.2 Linearization of cos(θ)

Problem Statement: linearize y=cos(θ) at theta tilde=π/2

Exercise 1.3 Linearization of x2

Problem Statement: linearize y=x2 at x tilde=1

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Control Systems Copyright © by sewsara and Valerie Jardon is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book