10

Nothing in life is to be feared.

It is only to be understood.

-Marie Curie

Statistics. This word usually sends my students into orbit with anxiety. But take heed of the words of scientist Marie Curie, above. The focus of this chapter is helping you to interpret univariate evaluation data. The focus here is on interpreting numerical information with as little pain as possible.

Statistical evaluation data generally come in three forms: univariate, bivariate and multivariate. I am guessing that these terms sound like “evaluation as a second language,” so let’s break them down. After breaking them down, we will go over the basic steps involved in interpreting a statistical table.

Interpreting univariate data

The term “univariate” refers to one group – looking at data from one topic, and sometimes one group. When you read the word “univariate,” focus in on “uni” which is derived from the Latin word for one (“unus”). In practice evaluation, we see univariate statistics used to describe the characteristics of a group – either demographic, clinical, or other. For example, a report on citizens’ level of community pride at one point in time is considered a piece of univariate data.

Looking at Table 10.1, we see a visual example of how univariate evaluation statistics are reported in a one group table. In this example, we are thinking back to our social worker doing community organizing work focused on fostering the improvement of community pride.

To read a table, slow yourself down by first reading the title of the table, to ground yourself in what you are about to read. Then, figure out what is presented in each of the columns – in this case a list of the measures, or variables in the evaluation, and a summary of the data taken from citizens participating in the project. Under the latter, you will notice the notation “N=331.” This is the total number of people participating in the evaluation.

At this point, you can start going row by row to critically consume the data. Looking at the third row, we see what may at first appear to be some gibberish, “% (n) or M (SD).” Actually, this row is telling us the format that data will be presented in, in the column below. Let’s take these symbols one at a time.

The symbol “%” refers to percentage who answered the question (listed in a given row) in the affirmative. The letter “n” refers to the number of people who answered the question (listed in a given row) in the affirmative. For example, under the “measures” column, you can see a row labelled “intention to remain in the community (yes/no).” This measure is known as a nominal variable. The words in quotations describe the measure, or variable for which data are being presented in the data row. As this is a percentage being reported, the “yes/no” notation indicates that the number listed in the table is the percent of people indicating yes versus no. In this case, 61.9% of people indicated that they did intend to stay in the community versus move away. This is good news for the evaluator!

The number “205” listed in a parenthesis next to the percentage indicates the number of people who said yes out of the total number of people participating in the evaluation. For that number, see the “citizen participants” column showing N=331, the total number of people participating in the evaluation.

Moving on, the capital letter “M” refers to the mean, or average, a “measure of central tendency.” This is one of the most commonly used univariate evaluation statistics. This measure is known as a continuous variable. The problem with the mean, however, is that sometimes, it can be misleading. For example, if I told you the mean fee-for-service rate United States social work clinicians charge per hour was $356, you might be surprised, thinking that the rate sounds high. The truth is, a mean is calculated from a number of values along a spectrum. And that is where the standard deviation comes in.

On the table, the letters “SD” refer to the standard deviation, which can loosely be thought of as a unit of measurement above and below the mean, similar to a margin of error. You can be one standard deviation above or below the mean, or two, or three. The standard deviation is always measured in the unit of the measure in question. Let’s go through an example to make this real.

Back to our example about fee-for-service rates while the mean was $356, if the standard deviation was $151, this would give us a better sense of the spectrum of rates clinicians charge around the country. Variations might relate to insurance type or use of a private pay system. As you can see, the standard deviation allows for the truth to come forward. Therefore, the standard deviation should *always* be reported with the mean as a way to give critical consumers the bigger picture around the mean.

Now that we have mastered the concepts of the mean and standard deviation, let us interpret the community pride scale from Table 10.1. On average, citizen participants scored 27.0 (SD=13.6) on the community pride scale. The community pride instrument used a 1-100 measurement with 1 coding as not proud of the community at all and 100 coding as extremely proud of the community. This does not bode well for our evaluator as 40.6 was the highest community pride score within one standard deviation of the mean.

We get that number by taking the average score, 27.0, and adding one standard deviation (13.6) to get 40.6. To get a better sense of how the mean and standard deviation work in this example, see Figure 10.1, below.

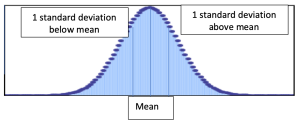
Figure 10.1 Mean and standard deviation

The percentage, mean and standard deviation are core concepts in evaluation statistics and are vital to understand when critically consuming bivariate data, which we will consider next.

Discussion questions for chapter 10

• Thinking of your current internship or work placement, how could you use univariate statistics to inform your work?