Índice 

1. Introducción
2. Primera ley: el Principio de Inercia
3. Segunda ley: el Principio de Masa
4. Tercera ley: el Principio de Interacción
5. La interacción gravitatoria
6. Cálculo de la velocidad de escape
7. Fuerzas derivadas de interacciones eléctricas: la fuerza elástica
8. Fuerzas derivadas de interacciones eléctricas: la fuerza de rozamiento
9. derivadas de interacciones eléctricas: la tensión

Dinámica de la partícula

 1_ INTRODUCCIÓN

Así como la cinemática que estudiamos en Física I es básicamente la obra de Galileo Galilei, la dinámica es, al menos en su primera formulación, la obra del gran sabio inglés Isaac Newton. En sus tres leyes básicas encontramos el fundamento de toda la mecánica elemental; por ello debemos examinarlas cuidadosamente.[1]

(Un agujero negro es realmente un objeto relativista y no debería ser analizado utilizando las fórmulas de la Física Clásica. Sin embargo, las correcciones relativistas alteran muy poco el cálculo efectuado aquí, que fuera realizado por primera vez por el geólogo Mitchell en el siglo XVIII.)

2_PRIMERA LEY: EL PRINCIPIO DE INERCIA

“Toda partícula en reposo, o en movimiento rectilíneo uniforme, permanece en ese estado hasta que se le aplique una fuerza exterior”.

En este enunciado, debemos distinguir dos ideas relacionadas entre sí pero no idénticas. Se trata del concepto de inercia, considerando esta como una propiedad de la materia, y del Principio de Inercia propiamente dicho.

Podemos definir la inercia como una propiedad de la materia según la cual esta se “opone”, se “resiste” al cambio de movimiento. En otras palabras, la materia, por sí misma, tiende a perseverar en su estado de movimiento. Si queremos que éste se modifique, debemos alterar el sistema de fuerzas aplicadas sobre la partícula en cuestión.

El Principio de Inercia nos dice entonces dos cosas: una de ellas puede resultarnos obvia, pero no es así con la restante. Todos sabemos que, si una partícula está en reposo, para que adquiera algún movimiento se le debe aplicar una fuerza. Pero no es tan obvio que, si la partícula se mueve con = constante, dicha velocidad será la misma hasta que se le aplique una fuerza determinada.

El Principio de Inercia, de apariencia tan sencilla, posee un sinnúmero de consecuencias. Estudiemos algunas de ellas:

1_ Consecuencias experimentales. Todos hemos vivido el efecto de la inercia en la vida diaria. Por ejemplo, cuando un auto arranca, nos parece que nos “vamos para atrás”. En realidad, por inercia, tendemos a permanecer en el mismo lugar, y el auto acelera hacia adelante. ¿Qué ocurre realmente cuando un auto frena de golpe?

2_ La relatividad de la trayectoria. Supongan que ustedes están sentados en un colectivo que se mueve con velocidad constante. Se entretienen arrojando una piedrita hacia arriba, la que cae en la mano que la había arrojado. Ustedes ven una trayectoria rectilínea. Pero un amigo que, en reposo respecto al andén, los observe desde afuera del colectivo, ve que la piedra describe una parábola. ¿Por qué? Porque en el instante de ser arrojada la partícula formaba parte del colectivo y se movía con la velocidad del mismo. Al tirarla, esta velocidad no “desaparece”, ya que la fuerza actuante sobre la partícula (el peso) sólo actúa en la dirección vertical. El amigo en reposo respecto al andén, entonces, ve que la piedra describe un tiro oblicuo, resultado de la composición de un movimiento con velocidad constante en el eje horizontal y un movimiento acelerado en dirección vertical. Por lo tanto, la relatividad de la trayectoria es una consecuencia del Principio de Inercia.

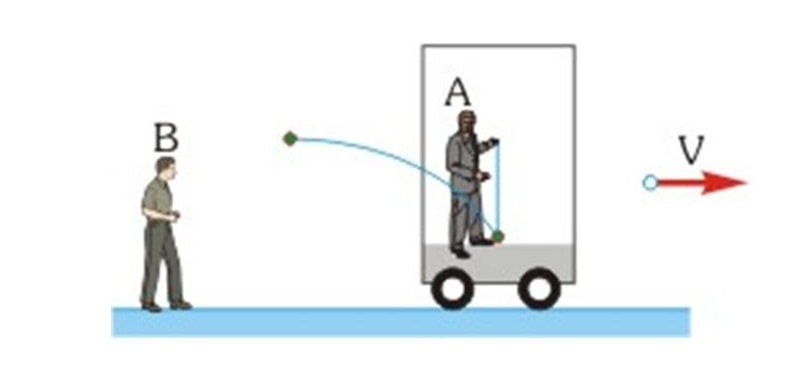
3_ El concepto de equivalencia. Supongamos que nos encontramos en el interior de un vehículo que no tiene ninguna posibilidad de comunicación con el exterior. Realizando un experimento en el interior del vehículo, ¿Podemos determinar si el mismo se encuentra en reposo o se mueve con respecto a Tierra? La respuesta es: no. ¿Por qué? Porque cualquier cosa que arrojemos, ya sea en forma oblicua, horizontal o vertical, o cualquier otro movimiento que intentemos conservará la velocidad que el vehículo eventualmente tiene en el eje del movimiento. Los resultados del experimento, entonces, serán iguales en ambos casos. Por lo tanto, el reposo y el movimiento rectilíneo uniforme son físicamente equivalentes.[1]

4_ La velocidad es una función continua del tiempo. Como resultado de la inercia, la velocidad no puede presentar “saltos”, sino que, al cambiar de un valor a otro, debe pasar por todos los valores intermedios. Por lo tanto, cuando representamos el resultado debe ser una función continua. No ocurre necesariamente lo mismo con la aceleración, como veremos más adelante.

5_ ¿Por qué, en el enunciado de este principio, hablamos de una fuerza “exterior”? Esto verdaderamente es redundante, porque al tratarse de una partícula todas las fuerzas son exteriores a la misma. Pero lo hemos indicado para acentuar un concepto básico de la mecánica newtoniana: “ninguna partícula se hace fuerza a sí misma” o, en otras palabras, la mecánica clásica newtoniana es una mecánica de partículas que se ejercen fuerzas unas a otras, es decir, es una mecánica de interacciones entre partícula.

6_ ¿Puede una partícula encontrarse en movimiento cuando la resultante de las fuerzas sobre la misma sea nula? Sí, siempre y cuando se mueva con velocidad constante; porque que la aceleración sea nula no implica necesariamente que también lo sea la velocidad.

7_ Inercia y masa. Quizás hasta ahora estemos acostumbrados a definir la masa un cuerpo como su “cantidad de materia”. Pero aquí se presenta el problema de definir qué es la materia, y si decimos que es “aquello que tiene masa” nos encontramos con un razonamiento circular. Pero la masa está relacionada con la inercia. Pensemos: ¿qué es más difícil de mover, o de modificar su movimiento, un bloque de 100 kg ó uno de 1 kg? Obviamente, el de 100 kg. Por lo tanto, al ser mayor su masa, lo mismo ocurre con su inercia. En consecuencia, la masa es una medida de la inercia.

Sobre la masa, tendremos algo más que decir más adelante.

3_SEGUNDA LEY: EL PRINCIPIO DE MASA

Antes de enunciarla, tenemos que definir una nueva magnitud física, vectorial, denominada la cantidad de movimiento, que simbolizamos con [latex]\vec{p}[/latex]  definimos como:

[latex]\vec{p}=m\vec{V}[/latex]

El Principio de Masa, entonces, es básicamente la definición del concepto de fuerza, en su relación con la cantidad de movimiento:

[latex]\sum \vec{F}=\frac{d\vec{p}}{dt}[/latex]

Es decir, la resultante de las fuerzas que actúan sobre una partícula es igual a la variación de la cantidad de movimiento de la misma, con respecto al tiempo.

Es posible que ustedes, al cursar Física en el Ciclo Básico Común, hayan visto esta ley expresada de otra forma, como:

[latex]\sum \vec{F}=m\vec{a}[/latex]

El enunciado que acabamos de dar es más general. Ahora bien, si suponemos que la masa de la partícula es constante, resulta:

[latex]\sum \vec{F}=\frac{d\vec{p}}{dt}=\frac{d(m\vec{V})}{dt}=m\frac{d\vec{V}}{dt}=m\vec{a}[/latex]

de donde la fórmula que ustedes conocen del Ciclo Básico Común es realmente un caso particular, consistente en la aplicación de la Segunda Ley de Newton para masa constante. Esta expresión, por ejemplo, no se podrá aplicar para estudiar el despegue de un cohete, debido a que la expulsión de los gases lo transforma en un sistema de masa variable[1].

Notemos que esta ley es enteramente consistente con la anterior, el Principio de Inercia. En efecto, si [latex]\sum \vec{F}=0[/latex]  resulta [latex]\vec{a}=0[/latex] y la partícula se mueve con [latex]\vec{V}[/latex]  constante, pero no tiene necesariamente que encontrarse en reposo.

Por otra parte, nuevamente aparece la idea de la masa como una medida de la inercia. Comparemos dos partículas de distinta masa sobre las que se aplican las mismas fuerzas. Claramente, para la partícula de mayor masa la aceleración será menor. Por lo tanto, cuanto mayor sea la masa de una partícula mayor será su “resistencia” a modificar su velocidad, es decir, será mayor su inercia.

El Principio de Masa es una de las expresiones más poderosas de toda la Física Clásica. Por ejemplo, de él pueden deducirse los Teoremas de Conservación. Al efecto, definamos una nueva magnitud, también de naturaleza vectorial [latex]\vec{J}[/latex], el impulso , definido como:

[latex]\vec{J}=\int \vec{F}dt[/latex]

En el caso que [latex]\vec{F}[/latex] sea constante resulta:

[latex]\vec{J}=\vec{F}\Delta t[/latex]

es decir, el producto de la fuerza por el intervalo de tiempo en el que ésta actúa.

Si ahora regresamos a la definición original del Principio de Masa:

[latex]\sum \vec{F}=\frac{d\vec{p}}{dt}\: \Rightarrow \: \sum \vec{F}dt=d\vec{p}[/latex]

e integrando de ambos miembros:

[latex]\int \sum \vec{F}dt=\int d\vec{p}[/latex]

Entonces:

[latex]\vec{J}=\Delta \vec{p}[/latex]

Por lo tanto, el impulso total aplicado sobre una partícula es igual es la variación de su cantidad de movimiento. Entonces, si

[latex]\vec{J}=0\: \Rightarrow \: \Delta \vec{p}=\vec{0}[/latex]

y la cantidad de movimiento de la partícula se mantiene constante. Este es el Teorema de Conservación de la Cantidad de Movimiento, el primero de una lista de diversos Teoremas de Conservación que resultan muy útiles para resolver problemas de mecánica. Dentro del ámbito clásico, todos estos teoremas son consecuencias del Principio de Masa, y se deducen integrándolo de una u otra forma[1].

La relación entre el impulso y la cantidad de movimiento es muy útil para interpretar físicamente situaciones que todos conocemos. Por ejemplo:

• – ¿Por qué cuando un boxeador recibe un golpe en la cara en lugar de retirar rápidamente la cara debe “acompañar” el golpe?
• – ¿Por qué si alguien cae desde una cierta altura sobre una lona elástica se “amortigua” la caída?

y la cantidad de movimiento de la partícula se mantiene constante. Este es el Teorema de Conservación de la Cantidad de Movimiento, el primero de una lista de diversos Teoremas de Conservación que resultan muy útiles para resolver problemas de mecánica. Dentro del ámbito clásico, todos estos teoremas son consecuencias del Principio de Masa, y se deducen integrándolo de una u otra forma[1].

La relación entre el impulso y la cantidad de movimiento es muy útil para interpretar físicamente situaciones que todos conocemos. Por ejemplo:

• – ¿Por qué cuando un boxeador recibe un golpe en la cara en lugar de retirar rápidamente la cara debe “acompañar” el golpe?
• – ¿Por qué si alguien cae desde una cierta altura sobre una lona elástica se “amortigua” la caída?

En ambos casos se trata de incrementar el tiempo que dura la colisión, lo que, a partir de las fórmulas precedentes, tiene como consecuencia la reducción de la fuerza recibida durante el impacto.

Nos resta decir algo más acerca del concepto de masa. Ya habíamos concluido que la masa puede interpretarse como una medida de la inercia.

Pero además, y aunque todavía no hicimos referencia a la fuerza gravitatoria, todos sabemos que se trata de una fuerza de atracción universal responsable de, entre otros fenómenos, la caída de los cuerpos. También sabemos que la fuerza gravitatoria depende de la masa y que, a mayor masa, mayor es la intensidad de la atracción gravitatoria. Pero aquí hemos utilizado el término “masa” en forma distinta a la empleada hasta ahora. La “masa” a la que nos referimos es la fuente de la interacción gravitatoria, y determina la intensidad de la misma. Existen, entonces, dos conceptos distintos a los que denominamos “masa”: la masa inercial, entendida como la medida de la inercia, y la masa gravitatoria, causa de la atracción universal.

Ahora, dejemos caer desde la misma altura dos cuerpos de distinta masa. Muchas veces hemos escuchado que, independientemente de la diferencia de masa, los cuerpos llegarán simultáneamente al piso, y efectivamente eso es correcto, si despreciamos la resistencia del aire. Pero, ¿Por qué?

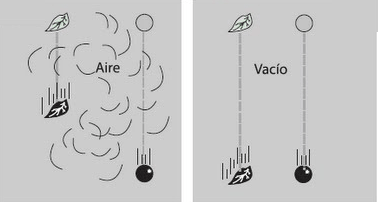
Que lleguen simultáneamente al piso implica que caen con igual aceleración. Nuevamente, nos preguntamos por qué.

La aparente contradicción surge porque, lógicamente, la atracción gravitatoria de la Tierra es mayor para el cuerpo de mayor masa. Éste, entonces, debería acelerarse más. Pero por tener mayor masa, también es mayor su inercia, es decir, su resistencia a acelerarse. La mayor atracción gravitatoria se compensa con la mayor inercia y entonces los dos cuerpos llegan simultáneamente al piso.

Este razonamiento es correcto, pero tiene una laguna. ¿Cuál es?

Es que estamos suponiendo que la mayor masa gravitatoria se compensa exactamente con la mayor masa inercial. Es decir, estamos suponiendo que:

masa gravitatoria=masa inercial

Dentro de la Mecánica Clásica, no hay manera de demostrar esto teóricamente, y sólo se acepta a partir de la evidencia experimental por el físico húngaro Lórand Eötvös, quien hacia fines del siglo XIX y principios del siglo XX, utilizando balanzas de torsión, midió con gran precisión la igualdad entre la masa inercial y la masa gravitatoria.

Esta igualdad se conoce como el Principio de Equivalencia Débil o Principio de Equivalencia de Galileo, y en la Teoría de la Relatividad no es un principio, sino que se deduce a partir de postulados más generales.

4_TERCERA LEY: EL PRINCIPIO DE INTERACCIÓN

Cuando pegamos un puñetazo en una pared, ¿por qué nos duele la mano? Porque la mano “siente” una fuerza de igual intensidad a la que ejerce sobre la pared. Un error común es creer que primero hay una fuerza “mano-pared”, la “acción”, y después la “reacción”, “pared-mano”. En realidad, ambas fuerzas aparecen simultáneamente, son el resultado de la interacción entre la mano y la pared. Este error quizás haya sido estimulado por la denominación “Principio de Acción y Reacción” que en muchas oportunidades se otorga a este principio. El término “Principio de Interacción” describe más apropiadamente el concepto, y puede enunciarse formalmente así:

“Si una partícula A interactúa con una partícula B aplicándole una fuerza , entonces la partícula B interactúa con A aplicándole una fuerza con el mismo módulo y la misma dirección que , pero de sentido contrario”.

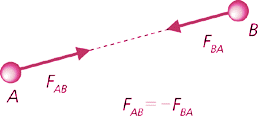
Las fuerzas, consecuencia de las interacciones, surgen siempre de a pares, se trata de los pares de interacción.

En la imagen, la interacción entre C y R da como resultado las dos fuerzas que se advierten. Notemos que están aplicadas en cuerpos distintos. Preguntamos: ¿qué ocurriría si las dos fuerzas que componen cada par de interacción estuvieran aplicadas en el mismo cuerpo? La respuesta es que nada podría acelerarse nunca, y por lo tanto nada podría abandonar el reposo.

Consideremos ahora la siguiente situación:

 

Una caja apoyada sobre el piso. ¿Qué fuerzas actúan sobre la caja? En primer lugar, el peso, resultado de la interacción gravitatoria entre la caja y la Tierra. Es una fuerza que la Tierra ejerce sobre la caja.

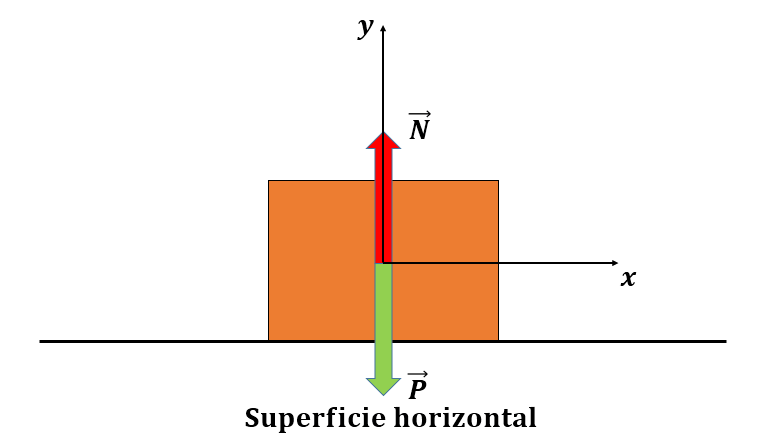
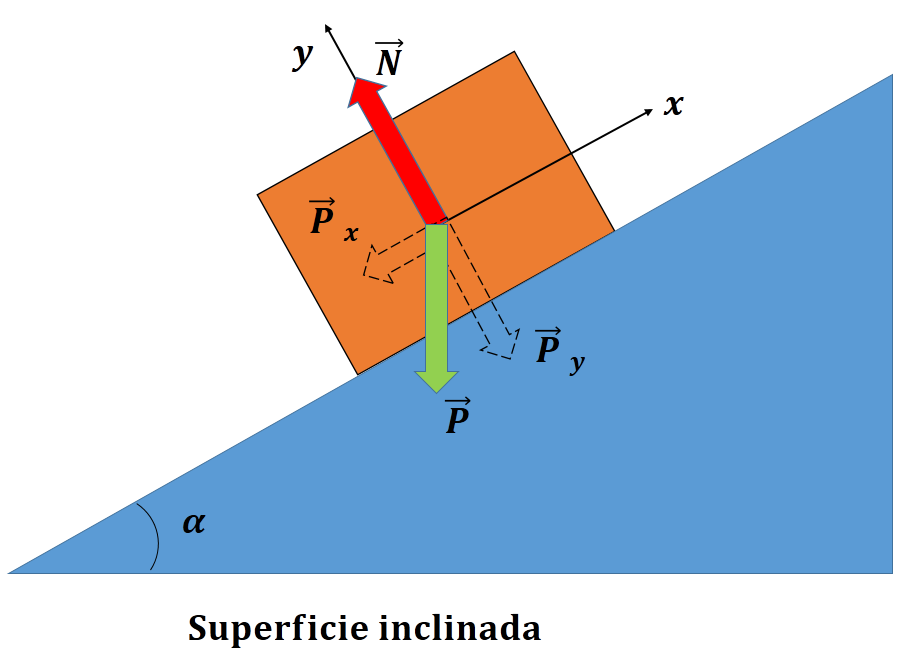
¿Dónde se encuentra su par de interacción? Se trata de una fuerza que la caja ejerce sobre la Tierra, y que dibujamos, hacia arriba, en esta última[1].

Ahora bien, si sobre la caja sólo actuase la fuerza peso, la caja se hundiría en el piso. Como esto no ocurre, tiene que existir una fuerza que el piso ejerce sobre la caja, perpendicular a la superficie de contacto, que llamaremos la Normal (N).

Un error frecuente es considerar que la Normal y el Peso (P) conforman un par de interacción; sin embargo, como la Normal es una fuerza que la superficie ejerce sobre la caja su par de interacción será una fuerza que la caja ejerce sobre la superficie, y está por lo tanto aplicada sobre esta última.

A continuación vemos algunos ejemplos de pares de interacción.

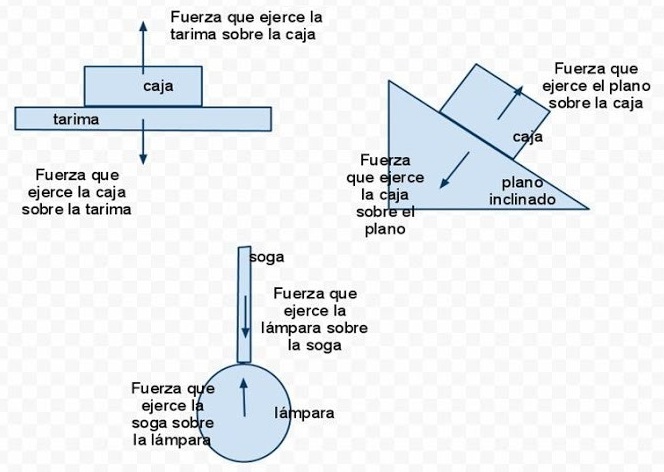
Volviendo ahora a las fuerzas aplicadas sobre la caja, notemos que entre la fuerza P y la N existe una diferencia importante. Si separamos la caja de la superficie de contacto, la fuerza peso sigue existiendo. Se trata, por lo tanto, de una interacción a distancia.

Por el contrario, cuando el contacto se suprime, desaparece N. Esta es, entonces, una fuerza de contacto.

Por otra parte, sabemos que el P es una consecuencia de la interacción gravitatoria. ¿De dónde resulta la N? Aunque superficialmente no lo parece es una fuerza de origen eléctrico, resultado de la interacción entre las nubes electrónicas de los átomos de las dos superficies en contacto. Se trata de una fuerza de tipo estadístico, resultante de la sumatoria de un enorme número de fuerzas elementales de naturaleza electromagnética.

Hasta ahora, por lo tanto, hemos encontrado dos fuerzas elementales, también conocidas como básicas o fundamentales: la gravitatoria y la electromagnética. Si bien no es este el lugar para profundizar en el tema, digamos que el cuadro completo de las Interacciones Fundamentales de la Naturaleza se completa con las dos clases de fuerzas nucleares: la fuerte y la débil. En el cuadro siguiente presentamos un panorama (muy simplificado) de estas cuatro interacciones.

En lo que sigue estudiaremos con más detalle la interacción gravitatoria, y algunas fuerzas estadísticas resultantes de la interacción electromagnética[1].

5_ LA INTERACCIÓN GRAVITATORIA

Ya sabemos que la interacción gravitatoria es una fuerza de atracción universal, que existe entre todas las masas. Su intensidad es muy débil; de hecho es la fuerza más débil de todas las existentes en la Naturaleza. Sin embargo, tratándose de una interacción acumulativa a medida que aumenta su fuente, es decir, la masa, se incrementa paralelamente la intensidad de la fuerza, y de ahí resulta la paradoja de que, siendo la más débil de todas las fuerzas, al mismo tiempo es la responsable de la estructura a gran escala del Universo. Que existan planetas, sistemas solares, galaxias, cúmulos de galaxias, es consecuencia de la interacción gravitatoria.

Quizás su aplicación más sencilla sea lo que denominamos el peso [latex]\vec{P}[/latex] de los cuerpos. Consideremos una partícula en caída libre a pequeña distancia de la superficie terrestre. Sobre ella, si despreciamos la resistencia del aire, la única fuerza actuante será su peso, es decir, la atracción gravitatoria ejercida por la Tierra, y su aceleración será la de la gravedad. Aplicando entonces el Principio de Masa resulta:

[latex]\vec{P}=m\, \vec{g}[/latex]

En realidad, la interacción gravitatoria no es constante, sino que depende de la distancia entre las partículas interactuantes. Consideremos entonces dos masas m₁ y m₂, separadas una distancia d.

El módulo de la fuerza gravitatoria entre ambas será:

[latex]\left |\vec{F} \right |=G\, \frac{m_{1}m_{2}}{d^{2}}[/latex]

siendo G la constante universal de gravitación, aproximadamente igual a:

[latex]G=6,67\times 10^{-11}\frac{Nm^{2}}{kg^{2}}[/latex]

Por lo tanto, la interacción gravitatoria es inversamente proporcional al cuadrado de la distancia entre las masas interactuantes.

Consideremos ahora un problema muy importante, tanto desde el aspecto conceptual como desde la historia de los conceptos de la dinámica. Supongamos que tenemos un ascensor, en el piso del mismo una balanza y sobre ésta una persona de masa m:

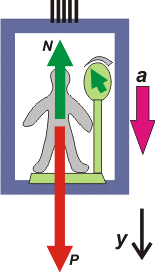
Queremos calcular lo que marca la balanza en una serie de situaciones diferentes. Primero comprendamos que la balanza no indica, en este caso, ni la masa ni el peso de la persona, sino la fuerza de contacto con la misma.

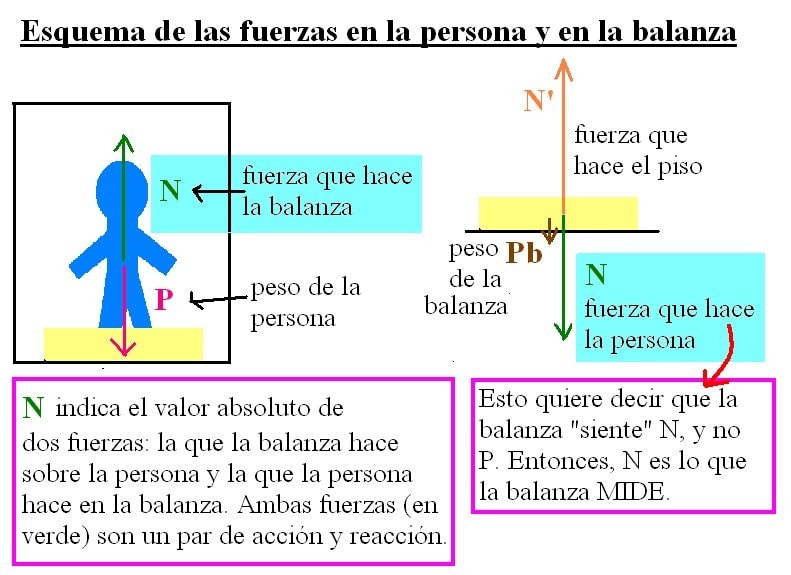
Como esta fuerza de contacto es el par de interacción correspondiente a la Normal, hallando esta última al mismo tiempo calculamos la indicación de la balanza.

Eligiendo sentido positivo hacia arriba y aplicando la Segunda Ley de Newton sobre el eje vertical:

N – mg = ma

siendo a la aceleración que el conjunto ascensor-balanza-persona pudiera tener.

Hallemos entonces N para las siguientes situaciones:

a) el conjunto se encuentra en reposo.

Resulta trivialmente a = 0 y por lo tanto N = mg, de donde la indicación de la balanza coincide con el peso de la persona.

b) el ascensor se mueve con velocidad constante.

Nuevamente, tenemos que a = 0 y N = mg. Esto es independiente de que el ascensor esté subiendo o bajando, mientras lo haga con velocidad constante. Por lo tanto, la situación es análoga al caso del reposo. Preguntamos: ¿Esto es sólo un resultado casual, consecuencia de este ejercicio en particular, o presenta un significado físico más profundo? La respuesta la encontramos en una de las consecuencias del Principio de Inercia: el reposo y el MRU son físicamente equivalentes. Por lo tanto, con experimentos realizados en el interior del ascensor no podremos diferenciar uno de otro.

c) el ascensor asciende con aceleración hacia arriba.

Para nuestro sistema de coordenadas es a > 0 y entonces N = ma + mg > mg. La balanza, por lo tanto, indica un valor superior al peso de la persona. Nuevamente preguntamos, ¿Cuál es la interpretación física de esto? Y otra vez la responde el Principio de Inercia: el ascensor acelera hacia arriba, pero por inercia la persona tiende a  mantenerse en la posición que tenía antes de acelerar. Por ello, se incrementa la fuerza de contacto entre la persona y la balanza.

d) el ascensor desciende con aceleración hacia arriba.

¿Es esto físicamente posible? Sí, simplemente los vectores velocidad y aceleración del sistema serán antiparalelos y el módulo de la velocidad del ascensor irá disminuyendo. El resultado es exactamente igual al caso anterior, N > mg . Por lo tanto, la aceleración determina el estado dinámico del sistema.

e) el ascensor desciende con aceleración hacia abajo.

Aquí resulta a < 0 y entonces N = ma + mg < mg. La balanza está indicando un valor inferior al peso de la persona. Sugerencia: interpreten este resultado a la luz del Principio de Inercia.

f) el ascensor asciende con aceleración hacia abajo.

Es igual que el anterior.

Y ahora, el caso más interesante. Supongamos que se cortan las cuerdas del ascensor y éste cae en caída libre.

g) caída libre.

Aquí, en módulo a=g, pero de acuerdo con nuestro sistema de coordenadas tiene signo negativo, por lo tanto:

N = 0

Es decir, la persona en el interior del ascensor experimenta una aparente situación de ausencia de gravedad.

¿Qué ocurre si en ese momento la persona deja caer una piedra? La piedra parece “flotar”, sin modificar su posición. Lo que ocurre es que, para un observador fijo a Tierra, todo el conjunto cae con la misma aceleración, y por lo tanto no se modifica la distancia relativa entre la persona y la piedra.

¿Por qué en una nave espacial que se encuentra orbitando en torno de la Tierra parecería no existir la gravedad? Es verdad que la atracción gravitatoria disminuye con el cuadrado de la distancia, pero para un cohete en órbita tal disminución no alcanza para que los efectos gravitatorios no sean observables. La explicación es que, como consecuencia de su movimiento orbital en torno de la Tierra, el cohete está “cayendo” instante a instante, y en cada momento reproduce la situación del ascensor en caída libre.

Finalmente, aunque se escape de los límites de este curso, hacemos un comentario “relativista”. La expresión:

N – mg = ma

puede reescribirse como:

N = m(a + g)

 

Por lo tanto, sería perfectamente aceptable interpretar el problema diciendo que, en el interior del ascensor la gravedad toma un valor diferente al habitual, dado por a + g. Es decir, el hecho que el ascensor esté acelerado genera un efecto equivalente a una modificación en el campo gravitatorio. Este sencillo problema de Física I inspiró a Albert Einstein su Teoría de la Relatividad Generalizada, en la que se preocupó por encontrar una explicación para el origen de la interacción gravitatoria. A partir de este problema podemos ver que hallarse sometido a la acción de un campo gravitatorio es equivalente a encontrarse en un sistema acelerado. De acuerdo con esto, la gravedad no es propiamente una fuerza, sino una consecuencia de las aceleraciones relativas entre las partículas. Pero aquí no podemos profundizar más en estas ideas.

6_ CÁLCULO DE LA VELOCIDAD DE ESCAPE

Supongamos por un momento que la atracción gravitatoria no existiera. Si en tal situación arrojamos una partícula verticalmente hacia arriba, ¿qué sucedería? La partícula, interpretada con el Principio de Inercia, se alejaría de nosotros en línea recta, y nunca caería.

Ahora, supongamos que la gravedad efectivamente existe, pero que es constante. Si volvemos a efectuar el tiro vertical, la partícula alcanzará una cierta altura máxima, y luego caerá. Si la velocidad inicial con la que arrojamos verticalmente la partícula se hace mayor, será mayor la altura máxima, pero siempre la partícula volverá a caer.

Y ahora, la situación más próxima a la realidad. La gravedad existe pero disminuye con el cuadrado de la distancia. Por lo tanto, cuando arrojamos algo verticalmente, experimentará en todo momento una fuerza que tiende a hacerlo regresar hacia la Tierra, pero cuanto mayor sea la altura alcanzada por la partícula, menor será la intensidad de dicha fuerza. Podemos entonces preguntarnos si existirá una velocidad de escape, es decir, alguna velocidad inicial para la cual, una vez arrojada la partícula, ésta se aleje indefinidamente de la Tierra y nunca regrese.

Elijamos entonces el origen de coordenadas en el centro de la Tierra y trabajemos sobre el eje radial eligiendo sentido positivo hacia el exterior. Un proyectil es arrojado verticalmente hacia arriba con una velocidad inicial  que es precisamente lo que queremos averiguar.

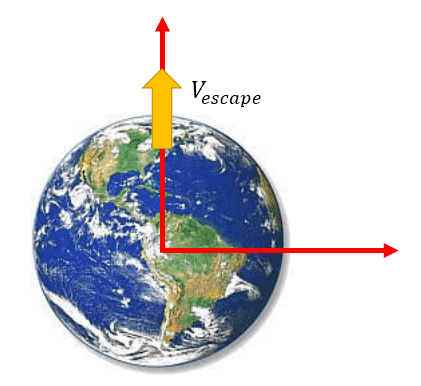
Despreciando cualquier otra contribución que no sea la de la fuerza gravitatoria y aplicando la Segunda Ley de Newton, tenemos que:

-F_g = ma

donde F_g es la fuerza gravitatoria, y , m y a son respectivamente la masa y la aceleración del proyectil.

Entonces:

[latex]-G\frac{m_{T}}{(R_{T}+h)^{2}}=\frac{dV}{dt}[/latex]

siendo  la masa de la Tierra,  el radio terrestre y h la posición del proyectil medida desde la superficie de la Tierra[1].

La ecuación anterior debe ser integrada. Como h depende del tiempo, no nos sirve pasar multiplicando dt y después integrar. Por ello, en el miembro derecho de la ecuación multiplicamos y dividimos por dh:

[latex]-G\frac{m_{T}}{(R_{T}+h)^{2}}=\frac{dV}{dt}\frac{dh}{dh}[/latex]

Como [latex]V=\frac{dh}{dt}[/latex] tenemos que:

[latex]-G\frac{m_{T}}{(R_{T}+h)^{2}}dh=V\, dV[/latex]

Integramos:

[latex]\int_{0}^{\infty }-G\frac{m_{T}}{(R_{T}+h)^{2}}dh=\int_{V_{escape}}^{0}V\, dV[/latex]

La condición para que la partícula “no regrese” es que su velocidad se vuelva nula recién en el infinito.

Resolviendo las integrales:

[latex]-\frac{G\, m_{T}}{R_{T}}=-\frac{1}{2}\, V_{escape}^{2}[/latex]

Entonces:

[latex]V_{escape}=\sqrt{2\frac{G\, m_{T}}{R_{T}}}[/latex]

Como, aproximadamente:

[latex]m_{T}=6\times 10^{24}kg[/latex]

[latex]R_{T}=6350\, km[/latex]

Obtenemos:

[latex]V_{escape}\cong 11,2 \: \frac{km}{s}[/latex]

Esa es entonces, en forma aproximada, la velocidad mínima que debe alcanzar un proyectil para abandonar en forma efectiva la superficie terrestre.

Una pregunta de divulgación científica: ¿Es posible invertir las incógnitas del problema y preguntar qué relación entre la masa y el radio debería tener un objeto para que la velocidad de escape correspondiente fuese igual a una velocidad determinada? Si suponemos que la misma es la velocidad de la luz, es decir, aproximadamente 300000 km/s, encontramos la relación entre la masa y el radio de un…agujero negro!

Una vez más, a partir de un sencillo problema de Física I llegamos a un concepto muy profundo de la Física contemporánea[1].

7_ FUERZAS DERIVADAS DE INTERACCIONES ELÉCTRICAS: LA FUERZA ELÁSTICA

Movimiento de un sistema masa-resorte

• Un bloque de masa m está atado a un resorte, el bloque puede moverse sin fricción sobre una superficie horizontal.
• Cuando el resorte no está ni comprimido ni estirado, el bloque está en su posición de equilibrio.
• X=0

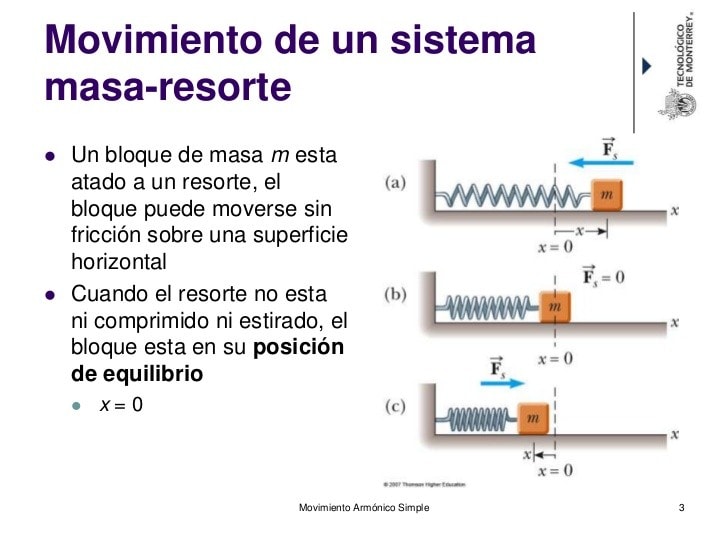
Cuando un resorte o un dispositivo equivalente se deforma, es decir, se estira o se comprime, entra en acción la fuerza elástica. Ésta no parece ser, macroscópicamente hablando, una fuerza de tipo eléctrico, pero en realidad resulta de la deformación experimentada por las nubes electrónicas de las moléculas que componen el resorte; su origen, por lo tanto, es efectivamente consecuencia de interacciones eléctricas.

Asumimos que el resorte cumple con la Ley de Hooke, según la cual la fuerza elástica [latex]\vec{F}_{e}[/latex] es directamente proporcional a la deformación del resorte:

[latex]\vec{F}_{e}=-k\Delta \vec{x}[/latex]

expresión en la que k es la constante elástica y la deformación experimentada por el resorte.

En la fórmula precedente es necesario formular algunas aclaraciones. En primer lugar, el signo negativo indica que la fuerza elástica tiene sentido contrario a la deformación del resorte, lo cual se puede comprobar fácilmente estirando o comprimiendo un resorte. No quiere decir que la fuerza sea “negativa”; por ello, cuando se escribe la Segunda Ley de Newton sobre un eje determinado, lo más práctico es tomar la fórmula anterior en módulo, [latex]\left |\vec{F}_{e} \right |=-k\left |\Delta \vec{x} \right |[/latex] y colocar a la [latex]\vec{F}_{e}[/latex] el signo que corresponda según el sistema de coordenadas que hayamos elegido.

La deformación [latex]\Delta \vec{x}[/latex] es, en valor absoluto, igual a [latex]\left | x-l_{0} \right |[/latex], con  la longitud natural del resorte, es decir, su longitud sin deformar. En general, es conveniente elegir un sistema de coordenadas en el que el origen coincida con l₀, de forma tal que podamos escribir, x en lugar de Δx.

La constante elástica k indica la “dureza” del resorte, es decir, su resistencia a la deformación. En realidad, k depende de diversos factores, tales como la temperatura y la presión, pero con buena aproximación puede suponerse constante.

Finalmente, digamos que la Ley de Hooke es, en sí misma, una expresión aproximada, correspondiente al primer término de un desarrollo en serie de Taylor.

Como un ejemplo de aplicación de la expresión de la fuerza elástica, calculemos la constante del resorte equivalente para dos resortes en paralelo.

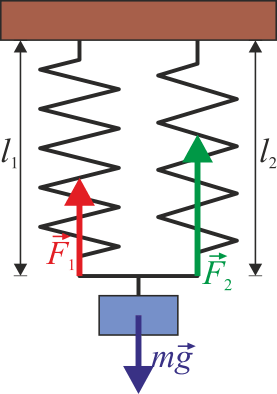
Supongamos entonces que una masa m se encuentra suspendida de dos resortes conectados como muestra la figura, de constantes k₁ y k₂ respectivamente. Suponemos que ambos resortes tienen la misma longitud natural, y hacemos coincidir el origen del sistema de coordenadas en dicha longitud.

Calcular la constante del resorte equivalente k_eq implica calcular la constante de un resorte imaginario que cumpla la misma función que los dos resortes “reales”.

Aplicando la Segunda Ley de Newton tenemos que:

mg – k₁x₁ – k₂x₂ = 0

dado que suponemos que el sistema se encuentra en equilibrio.

Ahora bien, en la realidad x₁ y x₂ podrían ser diferentes. Pero tal situación implicaría que ambos extremos de la masa m se encontrarían a distinta altura. La masa m no podría corresponder entonces a un cuerpo puntual. Por lo tanto, dado que trabajamos dentro del modelo de partícula tendremos que:

x₁ = x₂ = x

y

mg – (k₁+k₂)x = 0

Si trabajásemos con el resorte equivalente, tendríamos que:

mg – k_eqx = 0

y entonces:

k_eq = k₁+k₂

EJERCICIO 1:

Considere dos resortes conectados en serie:

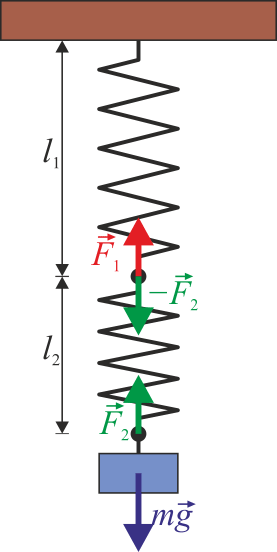
Demostrar que, en este caso, la constante del resorte equivalente es:

[latex]k_{eq}=\frac{k_{1}k_{2}}{k_{1}+k_{2}}[/latex]

Link a simulación con Geogebra:

Simulacion resorte Geogebra

8_ FUERZAS DERIVADAS DE INTERACCIONS ELÉCTRICAS: LA FUERZA DE ROZAMIENTO

La fuerza de fricción o de rozamiento es consecuencia de las rugosidades que poseen todas las superficies, las que determinan un conjunto de interacciones microscópicas entre las nubes electrónicas de las moléculas que las forman. El efecto macroscópico es lo que llamamos rozamiento o fricción, nuevamente una fuerza de tipo estadístico, resultante de un gran número de interacciones básicas de naturaleza eléctrica.

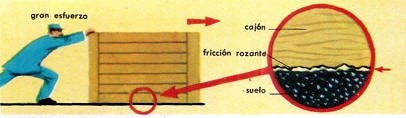
Supongamos entonces que empujamos un bloque, inicialmente en reposo, apoyado sobre el piso. Para ello, le aplicamos una fuerza [latex]\vec{F}[/latex]. El bloque no se mueve. ¿Por qué? Porque existe una fuerza [latex]\vec{F'}[/latex], de igual módulo y opuesta a [latex]\vec{F}[/latex], que la equilibra. Esta es la fuerza de rozamiento estático,[latex]\vec{F}_{est}[/latex] denominada así porque no existe desplazamiento relativo entre el bloque y la superficie de apoyo.

Esta fuerza está estrechamente relacionada con otra fuerza que ya conocemos: la Normal ([latex]\vec{N}[/latex]). Ambas, en realidad, son las dos componentes de la fuerza de contacto entre el bloque y la superficie de apoyo. La [latex]\vec{F}_{est}[/latex] es la componente de dicha fuerza paralela a la superficie de contacto, la [latex]\vec{N}[/latex], como su nombre lo indica, es la componente normal o perpendicular.

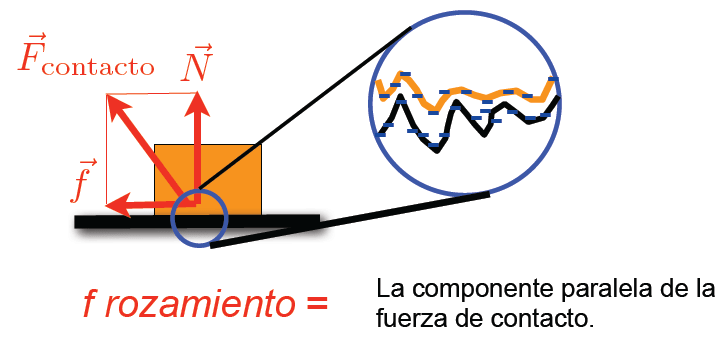
Ahora, supongamos que aumentamos la intensidad de la fuerza [latex]\vec{F}[/latex], pero el bloque continúa en reposo. Esto nos indica que la [latex]\vec{F}_{est}[/latex] no tiene un valor único, sino que aumenta en la medida en que aumentamos la intensidad de [latex]\vec{F}[/latex]. Sin embargo, llegará un instante en el que [latex]\vec{F}[/latex] sea lo suficientemente grande como para el bloque inicie su movimiento. Por lo tanto, la [latex]\vec{F}_{est}[/latex] no puede crecer indefinidamente, sino que alcanza un valor máximo, determinado, entre otros factores, por la naturaleza de las dos superficies en interacción.

Experimentalmente se comprueba que este valor máximo es:

[latex]F_{max}=\mu _{e}\, N[/latex]

donde [latex]\mu _{e}[/latex] es el coeficiente de rozamiento estático, un parámetro adimensional que se determina empíricamente.

Tenemos que, en general:

[latex]0\leq \mu _{e}\leq 1[/latex]

Decimos en general, porque existen algunos materiales que dan origen a fuerzas de rozamiento muy grandes, y en ellos es [latex]\mu _{e}> 1[/latex].

Preguntamos: ¿Es correcto decir que la “fuerza de rozamiento estático se opone al movimiento entre las superficies”? Enunciada de esa forma, la frase no es enteramente correcta. Consideremos, por ejemplo, una persona que camina llevando una bandeja en una de sus manos. De no existir el rozamiento, la bandeja permanecería en reposo, la mano avanza y finalmente la bandeja se cae. La bandeja permanece “pegada” a la mano y avanza con ésta debido a la fuerza de rozamiento estática. Por lo tanto, la expresión correcta es “la fuerza de rozamiento estático se opone al movimiento relativo entre las superficies”. La situación, en lo que concierne al rozamiento, es más compleja si en lugar de partículas consideramos cuerpos rígidos, y ese tema será tratado ampliamente en el lugar correspondiente.

Ahora, supongamos que la fuerza de rozamiento estática alcanzó su valor máximo, pero la fuerza que efectuamos sobre el bloque la supera y éste se pone en movimiento. El coeficiente de rozamiento, ahora dinámico, adopta un valor inferior al estático, y la fuerza de rozamiento dinámico se opone al movimiento relativo entre ambas superficies.

Podemos representar esta situación en el gráfico siguiente:

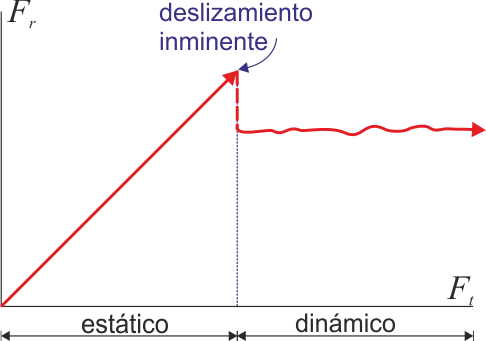
Siendo aproximadamente constante, la fuerza de rozamiento dinámico puede escribirse como:

[latex]F_{din}=\mu _{d}N[/latex]

con [latex]\mu _{d}[/latex] el coeficiente de rozamiento dinámico.

Habitualmente, y en concordancia con el gráfico presentado previamente, tenemos que:

[latex]\mu _{e}> \mu _{d}[/latex]

9_ FUERZAS DERIVADAS DE INTERACCIONES ELÉCTRICAS: LA TENSIÓN

Consideremos un problema como el que muestra la figura 17.

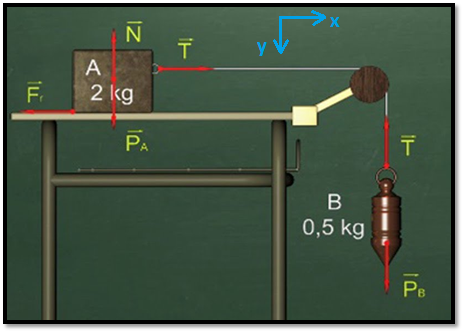
Hemos efectuado los diagramas de cuerpo libre, suponiendo que entre la mesa y la masa A no existe rozamiento. Ahora bien, ¿Por qué podemos afirmar que, en módulo, la tensión aplicada en la masa A es igual a la tensión sobre la masa B?

La tensión, la fuerza que mantiene tensa la cuerda, también reconoce un origen que, en último análisis, es eléctrico, del mismo modo que la fuerza elástica o la fuerza de rozamiento. Escribamos la segunda Ley de Newton sobre la cuerda, para lo cual nos imaginamos que la colocamos en forma horizontal. Tenemos que:

[latex]F_{B\rightarrow C}-F_{A\rightarrow C}=m_{c}\, a_{c}[/latex]

Siendo [latex]F_{B\rightarrow C}[/latex] la fuerza que la masa B ejerce sobre la cuerda,[latex]F_{A\rightarrow C}[/latex] la correspondiente a la masa A y m_ca_c el producto de la masa de la cuerda por su aceleración. Si suponemos que la cuerda es ideal su masa será despreciable; por lo tanto:

[latex]F_{B\rightarrow C}=F_{A\rightarrow C}[/latex]

Ahora bien,[latex]F_{B\rightarrow C}[/latex] es el par de interacción de la fuerza que la cuerda ejerce sobre B, es decir de la tensión, y por consiguiente ambas son iguales en módulo. Lo mismo ocurre para [latex]F_{A\rightarrow C}[/latex]. Transitivamente, entonces, las tensiones aplicadas sobre cada masa son, en módulo, iguales. Tener en claro que estas tensiones NO forman, entre sí, un par de interacción.

Vamos ahora resolver el problema, calculando la aceleración del sistema y la tensión de la cuerda en función de dos masas genéricas m_A, m_B y un μ_d también genérico.

Muy importante: elegimos un sistema de referencia fijo, tomando un sistema de coordenadas como muestra la figura 17.  Nunca cometer el error de tomar ejes “que se mueven junto con la cuerda” o algo parecido, porque se trataría de un sistema de referencia acelerado que, como veremos más adelante, se denomina sistema no-inercial y tiene características especiales que lo diferencia de los sistemas fijos.

Escribiendo entonces la Segunda Ley de Newton para el sistema de coordenadas indicado, tenemos:

masa A

x)  T – μ_dm_Ag = m_Aa

y)  m_Ag – N = 0

masa B

y)  m_Bg – T = m_Ba

Finalmente, resulta que:

[latex]a=\frac{m_{B}\, g-\mu _{d}\, m_{A}\, g}{m_{A}+m_{B}}[/latex]

Este cálculo fue sencillo, pero hay un detalle que debemos profundizar. Sin justificarlo, hemos asumido que, en módulo, ambas masas presentan la misma aceleración. Esto es consecuencia de que hemos supuesto que la cuerda que las une es inextensible. En este problema la igualdad de los módulos de las aceleraciones es evidente, pero no ocurre lo mismo en todas las situaciones. Existen, además, situaciones en las que las aceleraciones de las distintas masas son diferentes. Por lo tanto, necesitamos hallar un método formal que nos permita hallar analíticamente la relación de aceleraciones.

Para ello, fijemos nuestro sistema de coordenadas en la polea fija. Llamemos x_A e y_B a la posición de, respectivamente, cada una de las masas. Sea L la longitud de la cuerda. Tenemos que:

[latex]L=\left | x_{A} \right |+\left | y_{B} \right |[/latex]

Fue necesario colocar las barras de módulo para las coordenadas de posición debido a que la longitud de la cuerda debe ser la suma de términos positivos.

Para nuestro sistema de coordenadas:

L = -x_A + y_B

Derivando la expresión anterior dos veces respecto del tiempo, y teniendo en cuenta que L es constante, obtenemos:

0 = -a_A + a_B

Por lo tanto a_A = a_B = a

Ahora, veamos un problema en el que los módulos de las aceleraciones resultan diferentes.

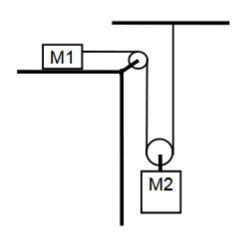
Notemos que, en este problema a diferencia del anterior, se introduce una polea móvil. Dicha polea también se considera ideal, por lo tanto sin masa; sin embargo, su aceleración debe tomarse en consideración.

Elijamos el mismo sistema de coordenadas que en el problema anterior, llamemos T a la tensión en la cuerda que une m₁ con la polea móvil y T´ la que une la polea con m₂. Suponemos que no existe rozamiento.

Planteando la Segunda Ley de Newton:

masa A

x)  T = m₁a₁

y)  m₁g – N = 0

masa B

y)  m₂g – T’ = m₂a₂

Polea móvil

y)  T’ – 2T= m_pa_p

Como suponemos que la masa de la polea es despreciable, resulta:

T’=2T

Ahora, hacemos lo mismo que en el problema anterior. Fijamos el sistema de coordenadas en la polea fija y, llamando y_p a la posición de la polea:

[latex]L_{1}=\left | x_{1} \right |+2\left | y_{p} \right |[/latex]

[latex]L_{2}=\left | y_{2} \right |-\left | y_{p} \right |[/latex]

donde L₁ y L₂ son las longitudes de cada una de las cuerdas.

Por lo tanto:

[latex]L_{1}= -x_{1}+2 \, y_{p}[/latex]

[latex]L_{2}= y_{2}- y_{p}[/latex]

Derivando:

[latex]0=-a_{1}+2\, a_{p}[/latex]

[latex]0=a_{2}- a_{p}[/latex]

Y entonces resulta:

[latex]a_{2}= a_{p}[/latex]

[latex]a_{1}= 2\, a_{2}[/latex]

La primera de las dos últimas relaciones es muy evidente; no así la segunda, por lo que el método presentado resulta útil para relacionar aceleraciones de cuerpos vinculados cuando tales relaciones no se pueden advertir intuitivamente.

Para cerrar el tema, consideremos esta cuestión: ¿Alcanza sólo con las Leyes de Newton para resolver un problema dinámico? La respuesta es no; hay que agregar las condiciones de vínculo.