5 Chapter 5 – Time value of Money valuing cash flow streams
Learning Objectives
- Value a series of cash flows, including streams, perpetuities, and annuities.
- Calculate the Present Value (PV) and Future Value (FV) of cash flows with constant or growing rates.
- Solve for unknown variables such as cash flows, interest rates, and periods in financial calculations.
- Apply valuation techniques to real-world scenarios like investments, loans, and retirement planning.
- Understand and analyze cash flow streams with non-annual payment structures.
5.1 Valuing a Stream of Cash Flows
5.1.1 What is a Cash Flow Stream?
A cash flow stream is a series of periodic cash inflows or outflows over a specified time period. These streams may be regular (e.g., monthly rent) or irregular (e.g., annual dividends). Understanding how to value these cash flows is crucial for making informed financial decisions, whether for investments, loans, or retirement planning.
The time value of money (TVM) underpins cash flow valuation. It recognizes that money available today is worth more than the same amount in the future due to its earning potential. This means that future cash flows must be discounted to determine their value today (Present Value, PV) or compounded to find their worth at a future date (Future Value, FV).
5.1.2 Key Concepts for Valuing Cash Flow Streams
1. Present Value of a Cash Flow Stream
The Present Value (PV) represents the current worth of future cash flows discounted at a specific rate. The formula is:
$$PV = \sum_{t=1}^n \frac{CF_t}{(1 + r)^t}$$
Where:
-
- CF_t: Cash flow at time t
- r: Discount rate per period
- t: Time period
- n: Total number of periods
2. Future Value of a Cash Flow Stream
The Future Value (FV) computes the worth of all cash flows at a specific future date, compounded over time:
$$FV = \sum_{t=1}^n CF_t \times (1 + r)^{n-t}$$
Where:
-
- CF_t: Cash flow at time t
- r: Interest rate per period
- n: Total number of periods
Detailed Example: Valuing a Cash Flow Stream Using Present Value
Scenario
A company is considering an investment that will generate the following cash inflows:
•Year 1: $5,000
•Year 2: $7,000
•Year 3: $6,000
The company requires a return of 8% (discount rate). Calculate the Present Value (PV) of the cash flow stream to determine whether the investment is worth pursuing.
Solution:
1. Apply the PV formula:
$$PV = \frac{5,000}{(1 + 0.08)^1} + \frac{7,000}{(1 + 0.08)^2} + \frac{6,000}{(1 + 0.08)^3}$$
2. Discount each cash flow:
-
- Year 1:
- $$PV_1 = \frac{5,000}{1.08} \approx 4,629.63$$
- Year 2:
- $$PV_2 = \frac{7,000}{1.1664} \approx 6,002.40$$
- Year 3:
- $$PV_3 = \frac{6,000}{1.2597} \approx 4,761.90$$
- Year 1:
3. Sum the discounted values:
PV = 4,629.63 + 6,002.40 + 4,761.90 = 15,393.93
Result:
The Present Value of the cash flow stream is $15,393.93.
Future Value of the Same Cash Flow Stream
Let’s calculate the Future Value (FV) of these cash flows at the end of Year 3:
1. Apply the FV formula:
$$FV = 5,000 \times (1 + 0.08)^2 + 7,000 \times (1 + 0.08)^1 + 6,000$$
2. Compound each cash flow:
-
- Year 1 (compounded for 2 years):
- $$FV_1 = 5,000 \times 1.1664 = 5,832.00$$
- Year 2 (compounded for 1 year):
- $$FV_2 = 7,000 \times 1.08 = 7,560.00$$
- Year 3 (no compounding):
- $$FV_3 = 6,000$$
- Year 1 (compounded for 2 years):
3. Sum the Future Values:
$$FV = 5,832.00 + 7,560.00 + 6,000 = 19,392.00$$
Result:
The Future Value of the cash flow stream is $19,392.00.
This is the value of the cash flows if the company waits until the end of Year 3 to collect all payments.
5.1.3 Applications of Cash Flow Stream Valuation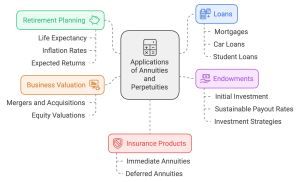
Retirement Planning: Calculating how much savings are needed to receive a fixed income during retirement is a crucial application of annuities and perpetuities. By treating retirement income as an annuity, financial planners can determine the lump sum needed at retirement to sustain a desired lifestyle. This involves considering factors such as life expectancy, inflation rates, and expected returns on investments.
Loans: Understanding the present value of regular payments is essential for both lenders and borrowers in various loan scenarios:
-
- Mortgages: Homebuyers can compare different mortgage options by calculating the present value of monthly payments over the loan term.
- Car Loans: Consumers can evaluate the true cost of auto financing by determining the present value of car loan payments.
- Student Loans: Graduates can assess the impact of different repayment plans by calculating the present value of their loan obligations.
Endowments: Establishing a fund that pays out a fixed amount indefinitely for scholarships or charity is a classic example of a perpetuity. Universities and non-profit organizations use this concept to:
-
- Determine the initial investment needed to support ongoing programs.
- Calculate sustainable annual payout rates that preserve the endowment's principal.
- Evaluate the long-term impact of different investment strategies on the fund's ability to provide consistent support.
Business Valuation: Companies use annuity and perpetuity concepts to estimate the value of businesses based on projected cash flows. This is particularly useful in:
-
- Mergers and acquisitions, where buyers assess the present value of a target company's future earnings.
- Equity valuations, where analysts use dividend discount models to price stocks.
Insurance Products: Life insurance companies design and price annuity products using these principles to provide customers with guaranteed income streams. This includes:
-
- Immediate annuities that start paying out right away.
- Deferred annuities that allow for an accumulation phase before payments begin.
Interactive Exercise
Scenario:
You are considering purchasing a business that will generate the following cash flows over the next 4 years:
- Year 1: $10,000
- Year 2: $12,000
- Year 3: $15,000
- Year 4: $18,000
The required discount rate is 6%. Calculate the Present Value (PV) of this cash flow stream.
Solution:
1.Apply the PV formula:
$$PV = \frac{10,000}{(1 + 0.06)^1} + \frac{12,000}{(1 + 0.06)^2} + \frac{15,000}{(1 + 0.06)^3} + \frac{18,000}{(1 + 0.06)^4}$$
2.Compute the discounted cash flows:
- Year 1:
- $$PV_1 = \frac{10,000}{1.06} \approx 9,433.96$$
- Year 2:
- $$PV_2 = \frac{12,000}{1.1236} \approx 10,676.53$$
- Year 3:
- $$PV_3 = \frac{15,000}{1.1910} \approx 12,594.70$$
- Year 4:
- $$PV_4 = \frac{18,000}{1.2625} \approx 14,271.24$$
3.Sum the discounted values:
$$PV = 9,433.96 + 10,676.53 + 12,594.70 + 14,271.24 = 46,976.43$$
Result:
The Present Value of the business is $46,976.43.
5.2 Perpetuity
5.2.1 What is a Perpetuity?
A perpetuity is a stream of equal cash flows that continues indefinitely. Unlike other cash flows with a fixed end date, perpetuities assume payments or receipts last forever. While infinite cash flows might seem theoretical, they are commonly used in finance for valuing specific assets like preferred stocks, real estate leases, or endowment funds.
5.2.2 Formula for Valuing a Perpetuity
The Present Value (PV) of a perpetuity is calculated using the formula:
[latex]PV = \frac{C}{r}[/latex]
Where:
-
- C: Cash flow per period (constant payment)
- r: Discount rate (as a decimal)
This formula works because the sum of an infinite series of discounted cash flows converges to a finite value.
Example: Valuing a Perpetuity
Scenario:
A university endowment fund generates $500,000 annually to support scholarships. If the discount rate is 5%, calculate the Present Value of the endowment fund.
Solution:
1.Identify the variables:
-
- C = 500,000
- r = 0.05
2.Apply the formula:
$$PV = \frac{C}{r} = \frac{500,000}{0.05} = 10,000,000$$
Result:
The Present Value of the endowment fund is $10,000,000. This means the university would need an initial investment of $10,000,000 at a 5% return to provide perpetual annual payments of $500,000.
5.2.3 Perpetuity with Growth
A growing perpetuity assumes cash flows grow at a constant rate (g) indefinitely. This is particularly useful in valuing stocks or other assets where payments or revenues are expected to increase over time.
$$PV = \frac{C}{r - g}$$
Where:
-
- C: Cash flow in the first period
- r: Discount rate (as a decimal)
- g: Growth rate of cash flows (as a decimal)
- r > g: The discount rate must exceed the growth rate for the formula to be valid.
Example: Growing Perpetuity
Scenario:
A company issues preferred stock paying an annual dividend of $5 per share, which grows at 2% per year. If investors require a 6% return, calculate the Present Value of the stock.
Solution:
1.Identify the variables:
-
- C = 5
- r = 0.06
- g = 0.02
2.Apply the formula:
$$PV = \frac{C}{r - g} = \frac{5}{0.06 - 0.02} = \frac{5}{0.04} = 125$$
Result:
The Present Value of the preferred stock is $125 per share.
5.2.4 Applications of Perpetuities in Finance
-
- University Endowments
Endowments use the perpetuity model to estimate the principal required to fund scholarships or programs indefinitely.
-
- Preferred Stock Valuation
Preferred stocks often provide fixed dividends indefinitely, making them a common application of perpetuity valuation.
-
- Real Estate Ground Rent
Certain lease agreements involve perpetual payments, such as ground rent, which can be valued using the perpetuity formula.
-
- Bond Valuation
Perpetual bonds, pay interest forever and are valued as perpetuities.
Interactive Exercise
Scenario:
A trust fund is set up to pay $20,000 annually to a beneficiary forever. The discount rate is 4%.
-
- Calculate the Present Value of the trust fund.
- What happens if the trust fund’s annual payment grows by 1% each year?
Solution:
-
- For constant payments:
-
- C = 20,000, r = 0.04
$$PV = \frac{C}{r} = \frac{20,000}{0.04} = 500,000$$
-
- For growing payments:
• C = 20,000, r = 0.04, g = 0.01
$$PV = \frac{C}{r - g} = \frac{20,000}{0.04 - 0.01} = \frac{20,000}{0.03} = 666,667$$
Results:
The Present Value with constant payments is $500,000.
The Present Value with 1% growth is $666,667.
Case Study: University Endowment Fund
Background:
Harvard University, one of the world’s most prestigious institutions, relies heavily on its endowment fund to finance a significant portion of its operations. The endowment fund is structured to provide an indefinite income stream to support scholarships, faculty salaries, and campus infrastructure. This setup models a perpetuity, where the university receives annual payments that are expected to last forever.
Objective:
To better understand how the concept of perpetuities applies to real-world financial scenarios, students will analyze the present value of Harvard’s endowment fund using the perpetuity formula.
Scenario:
Harvard’s endowment fund provides an annual cash flow of $400 million. The discount rate used by financial analysts for such investments is 5%.
Task:
-
- Calculate the present value (PV) of Harvard’s endowment fund using the perpetuity formula:
$$PV = \frac{C}{r}$$
Where:
-
-
- C = $400 million (annual cash flow)
- r = 0.05 (discount rate)
-
Questions for Analysis:
-
- What is the present value of Harvard’s endowment fund given the $400 million annual cash flow and a 5% discount rate?
- How would the present value change if the discount rate were to increase to 6%?
- Discuss how changes in the cash flow amount or discount rate could affect the sustainability of the university’s finances.
Reference:
For more information on university endowment structures and their importance, visit Harvard’s Financial Overview.
Discussion Points:
-
- How do perpetuities help universities plan for long-term financial stability?
- What are the risks associated with relying on a perpetuity model for income?
- Explore other real-world applications of perpetuities, such as preferred stock and ground rent in real estate.
Key Insights
-
- Constant Payments: Perpetuities are a straightforward way to model infinite streams of cash flows with constant payments.
- Growing Perpetuities: The inclusion of growth makes this model useful for dividends or payments expected to increase over time.
- Practical Applications: Perpetuities help in valuing endowments, stocks, bonds, and real estate scenarios.
5.3 Annuity
5.3.1 What is an Annuity?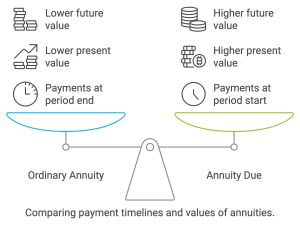
An annuity is a series of equal payments made at regular intervals over a specific period. These payments can represent either outflows (e.g., loan repayments) or inflows (e.g., investment returns). Unlike a perpetuity, an annuity has a definite start and end date.
5.3.2 Types of Annuities
-
- Ordinary Annuity: Payments occur at the end of each period (e.g., loan payments).
- Annuity Due: Payments occur at the beginning of each period (e.g., rent payments).
The difference lies in the timing of cash flows, which impacts their Present Value (PV) and Future Value (FV).
Formulas for Annuities
-
- Present Value of an Ordinary Annuity
The PV of an annuity calculates the value of future cash flows as a lump sum today:
$$PV_{\text{annuity}} = P \times \frac{1 - (1 + r)^{-n}}{r}$$
Where:
-
-
- P: Payment amount per period
- r: Interest rate per period (as a decimal)
- n: Total number of periods
-
-
- Future Value of an Ordinary Annuity
The FV of an annuity calculates how much the series of payments will be worth in the future:
$$FV_{\text{annuity}} = P \times \frac{(1 + r)^n - 1}{r}$$
Where:
-
- P: Payment amount per period
- r: Interest rate per period
- n: Total number of periods
Adjusting for Annuity Due
For an annuity due, multiply the PV or FV by (1 + r), since payments are made at the start of each period:
$$PV_{\text{annuity due}} = PV_{\text{ordinary annuity}} \times (1 + r)$$
$$FV_{\text{annuity due}} = FV_{\text{ordinary annuity}} \times (1 + r)$$
Example: Present Value of an Ordinary Annuity
Scenario
You plan to retire in 10 years and want to receive $10,000 per year for 15 years after retirement. The interest rate is 6% per year. How much money do you need to invest today to fund your annuity payments?
Step-by-Step Solution
1. Set Up the Formula:
Use the PV formula for an ordinary annuity:
$$PV_{\text{annuity}} = P \times \frac{1 - (1 + r)^{-n}}{r}$$
2. Substitute the Values:
-
- P = 10,000
- r = 0.06
- n = 15
$$PV_{\text{annuity}} = 10,000 \times \frac{1 - (1 + 0.06)^{-15}}{0.06}$$
3. Calculate Step-by-Step:
-
- $$(1 + 0.06)^{-15} = 0.4173$$
- $$1 - 0.4173 = 0.5827$$
- $$0.5827 / 0.06 = 9.7117$$
- $$PV_{\text{annuity}} = 10,000 \times 9.7117 = 97,117$$
Result
You need to invest $97,117 today to fund 15 years of $10,000 annual payments at 6% interest.
Example: Future Value of an Ordinary Annuity
Scenario
You save $5,000 annually for 10 years in an account earning 5% interest per year. What will be the Future Value of your savings?
Step-by-Step Solution
1. Set Up the Formula:
Use the FV formula for an ordinary annuity:
$$FV_{\text{annuity}} = P \times \frac{(1 + r)^n - 1}{r}$$
2. Substitute the Values:
-
- P = 5,000
- r = 0.05
- n = 10
$$FV_{\text{annuity}} = 5,000 \times \frac{(1 + 0.05)^{10} - 1}{0.05}$$
3. Calculate Step-by-Step:
-
- [latex](1 + 0.05)^{10} = 1.6289[/latex]
- [latex]1.6289 - 1 = 0.6289[/latex]
- [latex]0.6289 / 0.05 = 12.578[/latex]
$$FV_{\text{annuity}} = 5,000 \times 12.578 = 62,890$$
Result
Your savings will grow to $62,890 after 10 years.
Case Study: Retirement Planning with Annuities
Background:
Maria, a 45-year-old teacher, is planning for her retirement. She wants to retire at 65 and receive a steady income for 20 years after retirement. To achieve this, Maria is considering investing in an ordinary annuity that will start making annual payments at the end of each year once she retires.
Maria’s financial advisor has proposed an annuity plan where she will make equal annual contributions for the next 20 years, with an interest rate of 5% per year. The annuity will pay her $40,000 per year during retirement.
Objective:
Maria needs to evaluate the present value of the annuity to understand its current worth and determine if her contributions will be sufficient to meet her retirement needs.
Task:
-
- Calculate the total present value of the ordinary annuity payments she will receive during retirement using the following formula:
$$PV_{\text{annuity}} = P \times \frac{1 - (1 + r)^{-n}}{r}$$
Where:
-
-
- P = $40,000 (payment per period)
- r = 0.05 (annual interest rate)
- n = 20 (number of payment periods)
- Discuss how Maria’s financial situation might change if the interest rate fluctuates over time or if she decides to increase her annual contributions.
-
Questions for Analysis:
-
- What is the present value of Maria’s future annuity payments at the current 5% interest rate?
- If the interest rate were to decrease to 4%, how would that affect the present value of her annuity?
- How do ordinary annuities compare to annuities due in terms of payment structures and present value?
Reference:
To learn more about retirement annuities and their benefits, read Investopedia’s Guide on Retirement Annuities.
Discussion Points:
-
- Why might Maria consider an annuity due instead of an ordinary annuity for her retirement?
- How would the present value change if she opted for a variable annuity that depended on market performance?
- How do fixed and variable annuities align with different risk tolerances?
Applications of Annuities
1. Loan Payments:
Loan amortization schedules are based on the present value of an annuity, where each payment consists of interest and principal repayment.
2. Retirement Planning:
Annuities are a common tool for ensuring steady retirement income.
3. Savings Goals:
Future Value calculations for annuities help determine how much to save periodically to reach a specific financial goal.
4. Insurance Products:
Life insurance and pension plans often involve annuities to provide consistent payouts over time.
Interactive Exercise
Scenario:
You borrow $50,000 for a car loan at 6% annual interest, to be repaid over 5 years in equal annual payments. Calculate the annual payment amount.
Hint: Use the formula for PV of an ordinary annuity:
$$PV = P \times \frac{1 - (1 + r)^{-n}}{r}$$
Steps:
-
- PV = 50,000, r = 0.06, n = 5.
- Rearrange the formula to solve for P:
$$P = \frac{PV \cdot r}{1 - (1 + r)^{-n}}$$
Solution:
-
- Calculate the denominator:
$$](1 + 0.06)^{-5} = 0.7473$$
1 - 0.7473 = 0.2527
$$0.2527 / 0.06 = 4.2117$$
-
- Solve for P:
$$P = \frac{50,000}{4.2117} \approx 11,877.47$$
Answer:
Your annual payment is approximately $11,877.47.
Key Takeaways
-
- Ordinary Annuity vs. Annuity Due: Timing matters; payments made at the start of a period (annuity due) have a higher PV and FV than those made at the end (ordinary annuity).
- Applications in Finance: Annuities play a critical role in loans, retirement planning, and savings.
- Adjust for Frequency: If compounding occurs more frequently (e.g., monthly), adjust the interest rate (r) and number of periods (n) accordingly.
5.4 Growing Cash Flows
5.4.1 What are Growing Cash Flows?
Growing cash flows represent payments or receipts that increase at a constant rate over time. Unlike fixed cash flows, growing cash flows account for factors like inflation, revenue growth, or contract terms with escalation clauses. Financial tools like perpetuities and annuities can be adapted to model these scenarios.
Understanding how to value growing cash flows is critical for:
•Investment Valuation: Estimating future returns on investments.
•Retirement Planning: Assessing the impact of increasing withdrawals or contributions.
•Business Decisions: Evaluating contracts or leases with annual growth clauses.
1. Growing Perpetuity
A growing perpetuity is a series of cash flows that grow at a constant rate (g) indefinitely. This concept is widely used in finance, particularly in stock valuation models such as the Gordon Growth Model.
Formula for Growing Perpetuity
$$PV_{\text{growing perpetuity}} = \frac{C}{r - g}$$
Where:
-
- C: Cash flow in the first period
- r: Discount rate (as a decimal)
- g: Growth rate of the cash flows (as a decimal)
- Condition: r > g (the discount rate must exceed the growth rate).
Example 1: Valuing a Stock with Growing Dividends
Scenario:
A stock pays a dividend of $5 per year, which is expected to grow by 3% annually. Investors require a 10% return to hold the stock. Calculate the Present Value of the stock (its intrinsic value).
Step-by-Step Solution:
1.Identify the variables:
-
- C = 5
- r = 0.10
- g = 0.03
2.Apply the formula:
$$PV_{\text{growing perpetuity}} = \frac{C}{r - g} = \frac{5}{0.10 - 0.03} = \frac{5}{0.07} = 71.43$$
Result:
The stock’s intrinsic value is $71.43.
Example 2: Valuing an Endowment Fund
Scenario:
A university endowment must provide $1,000,000 annually, growing at 2% per year to account for inflation. If the discount rate is 6%, calculate the initial fund required.
Step-by-Step Solution:
1.Identify the variables:
-
- C = 1,000,000
- r = 0.06
- g = 0.02
2.Apply the formula:
$$PV_{\text{growing perpetuity}} = \frac{C}{r - g} = \frac{1,000,000}{0.06 - 0.02} = \frac{1,000,000}{0.04} = 25,000,000$$
Result:
The university needs $25,000,000 to fund the perpetuity.
Key Applications of Growing Perpetuities
-
-
- Stock Valuation: Used in the Dividend Discount Model to value shares with growing dividends.
- Endowment Funds: Universities or charities use this model to ensure perpetual payouts.
- Real Estate: Calculating property leases that escalate annually.
-
2. Growing Annuity
A growing annuity represents a series of cash flows that grow at a constant rate (g) over a finite period (n). Unlike a growing perpetuity, a growing annuity ends after a specified time.
Formula for Growing Annuity
$$PV_{\text{growing annuity}} = P \times \frac{1 - \left(\frac{1 + g}{1 + r}\right)^n}{r - g}$$
Where:
-
- P: Payment in the first period
- r: Discount rate (as a decimal)
- g: Growth rate of the cash flows (as a decimal)
- n: Total number of periods
- Condition: r > g (the discount rate must exceed the growth rate).
Example 1: Retirement Contributions
Scenario:
You plan to contribute $5,000 in the first year to a retirement account. Contributions will grow by 3% annually for 15 years, and the account earns an annual return of 7%. Calculate the Present Value of your contributions.
Step-by-Step Solution:
- Identify the variables:
-
- P = 5,000
- r = 0.07
- g = 0.03
- n = 15
- Apply the formula:
$$PV_{\text{growing annuity}} = 5,000 \times \frac{1 - \left(\frac{1 + 0.03}{1 + 0.07}\right)^{15}}{0.07 - 0.03}$$
- Simplify step-by-step:
-
- $$\frac{1 + g}{1 + r} = \frac{1.03}{1.07} = 0.9626$$
- Raise to the power of n: $$0.9626^{15} = 0.7417$$
- Subtract from 1: $$1 - 0.7417 = 0.2583$$
- Divide by r - g: $$0.2583 / 0.04 = 6.4575$$
- Multiply by P: $$5,000 \times 6.4575 = 32,287.50$$
Result:
The Present Value of your contributions is approximately $32,287.50.
Example 2: Growing Rental Income
Scenario:
A property generates $10,000 in rent during the first year, growing at 2% annually. The lease lasts for 10 years, and the discount rate is 5% per year. Calculate the Present Value of the rental income.
Step-by-Step Solution:
1.Identify the variables:
-
- P = 10,000
- r = 0.05
- g = 0.02
- n = 10
2.Apply the formula:
$$PV_{\text{growing annuity}} = 10,000 \times \frac{1 - \left(\frac{1 + 0.02}{1 + 0.05}\right)^{10}}{0.05 - 0.02}$$
3.Simplify step-by-step:
-
- $$\frac{1 + g}{1 + r} = \frac{1.02}{1.05} = 0.9714$$
- Raise to the power of n: $$0.9714^{10} = 0.7812$$
- Subtract from 1: $$1 - 0.7812 = 0.2188$$
- Divide by r - g: $$0.2188 / 0.03 = 7.2933$$
- Multiply by P: $$10,000 \times 7.2933 = 72,933$$
Result:
The Present Value of the rental income is $72,933.
Key Applications of Growing Annuities
-
-
- Retirement Planning: Estimating the value of increasing contributions or withdrawals.
- Leases: Valuing contracts with annual escalation clauses.
- Project Evaluation: Calculating the value of revenues or costs that grow over a finite time.
-
Interactive Exercise
Scenario:
You are considering investing in a project with the following cash flows:
-
- Year 1: $2,000
- Growing by 5% annually for the next 8 years.
The required rate of return is 8%. Calculate the Present Value of the project’s cash flows.
Hint: Use the growing annuity formula:
$$PV_{\text{growing annuity}} = P \times \frac{1 - \left(\frac{1 + g}{1 + r}\right)^n}{r - g}$$
Key Takeaways
-
- Growing Perpetuity: Models indefinite cash flows with constant growth, common in stock valuation and endowments.
- Growing Annuity: Captures finite cash flows with growth, useful for leases, retirement, and project analysis.
- Practical Insights: These tools help account for growth in financial scenarios, improving valuation accuracy.
5.5 Solving for Variables Other Than Present Value or Future Value
5.5.1 Introduction
In many financial scenarios, the problem is not determining the Present Value (PV) or Future Value (FV) but solving for other variables such as:
-
- Cash Flows: How much must be deposited or withdrawn each period?
- Rate of Return: What is the interest rate or return required to achieve a financial goal?
- Number of Periods: How long will it take to reach a specific financial target?
This section explains how to rearrange key time value of money formulas to solve for these variables.
-
- Solving for Cash Flows
Scenario
You want to know how much you need to save or pay each period to achieve a specific FV or PV.
Formula
The formula depends on whether you are solving for an annuity or a growing annuity.
For an Ordinary Annuity:
Example: Saving for a Future Goal
Scenario:
You want to save $100,000 in 10 years by making equal annual contributions to an account earning 5% interest per year. How much do you need to contribute each year?
Step-by-Step Solution:
1.Identify the variables:
-
- FV = 100,000
- r = 0.05
- n = 10
2.Use the FV formula for an ordinary annuity:
$$\large P = \frac{FV}{\frac{(1 + r)^n - 1}{r}}$$
3.Substitute the values:
$$\large P = \frac{100,000}{\frac{(1 + 0.05)^{10} - 1}{0.05}}$$
4.Simplify step-by-step:
$$(1 + 0.05)^{10} = 1.6289$$
$$1.6289 - 1 = 0.6289$$
$$0.6289 / 0.05 = 12.578$$
$$P = 100,000 / 12.578 = 7,952.29$$
Result:
You need to save $7,952.29 annually to reach your goal.
2. Solving for the Rate of Return
Scenario
You need to determine the interest rate or return required to achieve a specific FV or PV over a given number of periods.
Formula
The rate of return is calculated using the PV or FV formulas and solving for r. However, this requires iteration or financial calculators for most cases. The general FV formula is:
$$\large r = \left(\frac{FV}{PV}\right)^{\frac{1}{n}} - 1$$
Example: Determining the Rate of Return
Scenario:
You invest $10,000 today, and it grows to $20,000 in 8 years. What is the annual rate of return?
Step-by-Step Solution:
1.Identify the variables:
-
- PV = 10,000
- FV = 20,000
- n = 8
2.Use the formula:
$$
\Large r = \left(\frac{FV}{PV}\right)^{\frac{1}{n}} - 1
$$
3.Substitute the values:
$$\Large r = \left(\frac{20,000}{10,000}\right)^{\frac{1}{8}} - 1 = (2)^{\frac{1}{8}} - 1$$
4.Calculate:
$$\Large 2^{\frac{1}{8}} = 1.0905$$
1.0905 - 1 = 0.0905
Result:
The annual rate of return is 9.05%.
3. Solving for the Number of Periods
Scenario
You need to determine how long it will take for an investment to grow to a specific FV or to pay off a loan given a fixed payment.
Formula
To calculate n, use logarithms to solve the exponential equation:
\[
n = \frac{\ln\left(\frac{FV}{PV}\right)}{\ln(1 + r)}
\]
Example: Determining the Time to Reach a Goal
Scenario:
You invest $5,000 at 6% annual interest, and you want it to grow to $10,000. How many years will it take?
Step-by-Step Solution:
1.Identify the variables:
-
- PV = 5,000
- FV = 10,000
- r = 0.06
2.Use the formula:
$$n = \frac{\ln\left(\frac{FV}{PV}\right)}{\ln(1 + r)}$$
3.Substitute the values:
$$n = \frac{\ln\left(\frac{10,000}{5,000}\right)}{\ln(1 + 0.06)}$$
4.Calculate step-by-step:
-
- $$\ln(10,000 / 5,000) = \ln(2) = 0.6931$$
- $$\ln(1 + 0.06) = \ln(1.06) = 0.0583$$
- $$n = 0.6931 / 0.0583 = 11.89$$
Result:
It will take approximately 11.89 years for your investment to double.
5.5.2 Applications of Solving for Other Variables
1. Personal Finance:
-
- Calculate how much to save annually for retirement.
- Determine how long it will take to pay off a mortgage.
2. Investment Decisions:
-
- Assess the required rate of return for a project or stock.
- Estimate how long it will take for an investment to double in value.
3. Business Finance:
-
- Determine the time to recover the initial investment in a project.
- Calculate loan payments or terms.
Interactive Exercises
1. Solving for Cash Flow
You want to accumulate $50,000 in 5 years in an account earning 4% interest. How much must you deposit annually?
2. Solving for Rate of Return
You invest $25,000 today and want it to grow to $50,000 in 10 years. What annual return is required?
3. Solving for Number of Periods
You deposit $2,000 at 5% annual interest. How long will it take to grow to $4,000?
Key Takeaways
-
-
- Cash Flow: Use annuity formulas to solve for periodic savings or payments.
- Rate of Return: Determine the return needed to meet financial goals using the FV/PV ratio.
- Number of Periods: Logarithmic calculations help estimate the time required to reach a target.
-
Example Case: Real Estate Developer Evaluating a New Project
Scenario
A real estate developer is assessing a potential project that requires an initial investment of $10,000. The project is expected to generate annual cash inflows of $3,000 for the next 5 years. The developer uses a discount rate of 8%, reflecting the opportunity cost of capital and the risk of the investment. The objective is to calculate the Net Present Value (NPV) to determine if the project is profitable and worth pursuing.
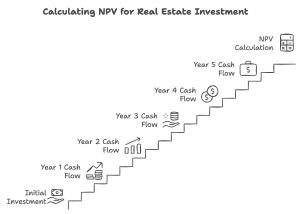 Key Information
Key Information
- Initial investment (C_0): $10,000
- Annual cash inflows (CF_t): $3,000 for 5 years
- Discount rate (r): 8% or 0.08
- Time period (t): 5 years
Step-by-Step Calculation of NPV
To calculate NPV, use the formula:
$$NPV = \sum_{t=1}^{n} \frac{CF_t}{(1 + r)^t} - C_0$$
Where:
- CF_t = Cash flow in year t
- r = Discount rate
- t = Time period (1 to 5 years)
- C_0 = Initial investment
1. Discount Each Annual Cash Flow to Present Value (PV):
$$PV_1 = \frac{3,000}{(1 + 0.08)^1} = \frac{3,000}{1.08} = 2,777.78$$
$$PV_2 = \frac{3,000}{(1 + 0.08)^2} = \frac{3,000}{1.1664} = 2,571.43$$
$$PV_3 = \frac{3,000}{(1 + 0.08)^3} = \frac{3,000}{1.2597} = 2,380.95$$
$$PV_4 = \frac{3,000}{(1 + 0.08)^4} = \frac{3,000}{1.3605} = 2,205.13$$
$$PV_5 = \frac{3,000}{(1 + 0.08)^5} = \frac{3,000}{1.4693} = 2,042.64$$
2. Sum the Present Values of All Cash Inflows:
$$\text{Total PV of Cash Inflows} = 2,777.78 + 2,571.43 + 2,380.95 + 2,205.13 + 2,042.64 = 11,977.93$$
3. Subtract the Initial Investment (C_0):
$$NPV = 11,977.93 - 10,000 = 1,977.93$$
Conclusion
The Net Present Value (NPV) of the project is $1,977.93. Since the NPV is positive, the project is expected to generate more value than it costs. This indicates that the project is profitable and should be considered a worthwhile investment.
Analysis and Discussion Points
1. Impact of a Higher Discount Rate:
- If the discount rate increases to 10%, how would the NPV change? (Answer: It decreases because the present value of future cash flows would shrink.)
2. Sensitivity to Cash Flow Estimates:
- What happens if the annual cash inflows are lower than expected, say $2,500 instead of $3,000?
- How does a delay in cash inflows (e.g., starting in Year 2) affect the NPV?
3. Other Factors to Consider:
- Non-financial factors like project feasibility, market conditions, and regulatory risks.
- Alternative investment opportunities with similar risks and returns.
Key Takeaways
- Valuing cash flow streams involves calculating their present and future values, providing a foundation for financial decision-making in both personal and business contexts.
- Perpetuities offer indefinite cash flows, commonly used for endowments, preferred stock, and perpetual bonds, while growing perpetuities incorporate inflation or growth into valuation.
- Annuities represent fixed payments over a set period, with broad applications in loans and savings, while growing annuities address cash flows that increase over time.
- Solving for variables like cash flows, rate of return, or the number of periods enhances the versatility of time value of money equations, enabling more tailored financial planning.
- These concepts and formulas apply to real-world scenarios such as retirement planning, loan repayments, investment goals, and project evaluations. Financial calculators or tools can streamline complex calculations.
Exercises
Conceptual Questions
- What is the difference between a perpetuity and an annuity? Provide an example of when each might be used in real life.
- Explain why the discount rate must be greater than the growth rate for valuing growing perpetuities and growing annuities.
- Why do ordinary annuities have a lower present value than annuities due, assuming the same cash flows and discount rates?
- Describe how growing cash flows account for inflation in financial planning and investment valuation.
Short Calculations
1. Present Value of a Cash Flow Stream
A business expects to receive cash inflows of $3,000, $4,000, and $5,000 over the next three years. If the discount rate is 7%, calculate the present value of these cash flows.
2. Future Value of an Ordinary Annuity
You save $1,500 annually in an account earning 6% interest, compounded annually, for 10 years. What will be the total savings at the end of 10 years?
3. Valuing a Perpetuity
A scholarship fund pays $20,000 annually in perpetuity. If the fund earns a return of 4%, what is its present value?
4. Valuing a Growing Perpetuity
A real estate property generates $10,000 in rental income annually, increasing by 2% each year. If the discount rate is 6%, what is the value of this perpetuity?
Scenario-Based Problems
1. Retirement Planning with Annuities
You plan to retire in 20 years and want to receive $50,000 annually for 25 years during retirement. The interest rate is 5%.
- How much money do you need at retirement to fund your annuity payments?
- If you start saving today with equal annual contributions, how much do you need to save each year for the next 20 years?
2. Growing Annuity for a Lease Agreement
A company leases office space for $12,000 in the first year, with the rent increasing by 3% annually. The lease lasts for 8 years, and the discount rate is 6%. What is the present value of the lease payments?
Case Study: Stock Valuation Using a Growing Perpetuity
Scenario
TechCo Inc. pays a dividend of $3 per share, expected to grow at 4% annually. Investors require a 10% return to hold the stock.
Tasks
- Calculate the intrinsic value of TechCo’s stock using the growing perpetuity formula.
- Discuss how a higher growth rate or lower required return would affect the stock’s value.
- If the stock is currently trading at $60, is it overvalued or undervalued based on your calculations?
Interactive Challenge
Question
You aim to save $100,000 in 15 years. You can either:
- Deposit $50,000 today in an account earning 5% interest annually.
- Save a fixed amount annually in the same account over the 15 years.
Tasks
- Calculate the future value of Option 1.
- Determine the annual savings required for Option 2.
- Which option is more feasible for your financial situation?
