6 Chapter 6 – Bonds

6.1 Introduction to Bonds and Basic Bond Features

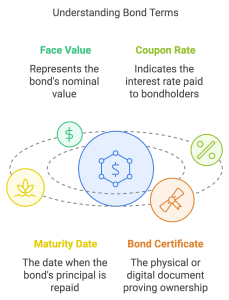
6.1.1 Bond Terminology and Structure

Bonds are financial instruments that represent a loan made by an investor to a borrower, typically a corporation or government. These are widely used to raise capital for large projects, public infrastructure, or business expansion. Understanding the terminology and structure of bonds is fundamental for evaluating them as investments.

1. Bond Certificate and Maturity Date

• • The bond certificate is the formal agreement that outlines the terms of the bond, including the issuer, maturity date, coupon rate, and face value.
  • The maturity date is when the issuer repays the bond’s face value, marking the end of the bond’s life.

2. Face Value (or Principal)

• • The face value, also called the par value or principal, is the amount paid back to the investor at maturity. Most bonds have a face value of $1,000.
  • This amount is crucial as it determines the bond’s coupon payments.

3. Coupon Payments and Coupon Rate

• • Bonds often provide periodic interest payments, called coupon payments, based on the coupon rate.
  • The coupon rate is expressed as a percentage of the face value and is typically fixed. For example, a bond with a 5% coupon rate on a $1,000 face value will pay $50 annually.

6.1.2 Calculating Coupon Payments

The formula for calculating coupon payments is straightforward:

[latex]\text{Coupon Payment (CPN)} = \frac{\text{Coupon Rate} \times \text{Face Value}}{\text{Number of Payments per Year}}[/latex]

Example Calculation

Suppose a bond has:

• • Face Value: $1,000
  • Coupon Rate: 6%
  • Semiannual Payments

The semiannual coupon payment would be:

[latex]\text{CPN} = \frac{6\% \times 1,000}{2} = \$30[/latex]

This means the investor receives $30 every six months until the bond matures.

6.1.3 Benefits of Bond Investments

1. Predictable Income

•Bonds provide regular, predictable cash flow, making them attractive for income-focused investors like retirees.

2. Capital Preservation

•For high-credit-quality bonds (e.g., U.S. Treasury bonds), there is minimal risk of losing the principal.

3. Portfolio Diversification

•Bonds often behave differently from stocks, providing stability during market volatility.

6.1.4 Comparison of Government and Corporate Bonds

1. Government Bonds

•Issued by national or local governments, these are considered low-risk.

•Examples: U.S. Treasury bonds, municipal bonds.

2. Corporate Bonds

•Issued by companies, these typically offer higher yields to compensate for increased credit risk.

Extended Example

A government bond with a face value of $1,000, a 3% coupon rate, and annual payments provides $30 per year.

In contrast, a corporate bond with a face value of $1,000 and a 6% coupon rate pays $60 per year, but carries a higher risk of default.

6.2 Zero-Coupon Bonds

6.2.1 Zero-Coupon Bond Cash Flows

Zero-coupon bonds are a unique type of debt security that does not make periodic interest (coupon) payments. Instead, these bonds are issued at a discount to their face value and repay the full face value at maturity. The difference between the purchase price and the face value represents the bondholder’s return. For example, if you purchase a zero-coupon bond with a face value of $1,000 for $800, you earn $200 in interest over the bond’s life. These bonds are popular for their simplicity and are commonly used for specific financial goals, such as saving for future expenses.

The formula for pricing zero-coupon bonds is as follows:

[latex]Price = Face Value / (1 + r)^n[/latex]

where r is the discount rate (yield to maturity), and n is the number of periods until maturity.

For example, suppose an investor purchases a zero-coupon bond with a face value of $1,000, maturing in 5 years, at a discount rate of 6%. The price of the bond would be:

[latex]Price = 1000 / (1 + 0.06)^5 = 747.26[/latex]

This means the investor pays $747.26 today and receives $1,000 when the bond matures in 5 years. The difference of $252.74 represents the investor’s earnings.

Zero-coupon bonds are especially attractive for investors with a specific financial goal and timeline, such as funding college tuition or retirement. By locking in the return now, they eliminate the uncertainty of market fluctuations, assuming the bond is held to maturity.

Applications of Zero-Coupon Bonds

Zero-coupon bonds are widely used in several financial contexts, such as retirement accounts, education savings plans, and funding future liabilities. For example, parents saving for a child’s college tuition can purchase a zero-coupon bond maturing in 18 years, knowing precisely how much they will receive at that time. Additionally, these bonds are used as benchmarks for risk-free rates, particularly in government-issued bonds like U.S. Treasury STRIPS.

6.2.2 Yield to Maturity of a Zero-Coupon Bond

The yield to maturity (YTM) of a zero-coupon bond is the annualized rate of return an investor earns if the bond is held until maturity. Since zero-coupon bonds do not provide periodic payments, the YTM reflects the bondholder’s total return over the life of the bond, accounting for the difference between the purchase price and the face value.

The formula for calculating YTM is derived from the zero-coupon bond pricing formula:

[latex]YTM = (Face Value / Price)^(1/n) - 1[/latex]

Where:

• • Face Value is the amount paid to the bondholder at maturity.
  • Price is the bond’s current purchase price.
  • n is the number of periods until maturity.

Comparing Different Maturities and Prices

Let’s examine how the time to maturity and purchase price affect the YTM. Consider two bonds:

• • Bond A: 5-year maturity, purchased for $800, face value of $1,000.
  • Bond B: 10-year maturity, purchased for $600, face value of $1,000.

For Bond A:

[latex]YTM = (1000 / 800)^(1/5) - 1[/latex]

[latex]YTM ≈ 0.0466 or 4.66%[/latex]

For Bond B:

[latex]YTM = (1000 / 600)^(1/10) - 1[/latex]

[latex]YTM ≈ 0.0519 or 5.19%[/latex]

As seen, longer maturities often result in higher YTMs for the same face value when the purchase price is lower. This highlights the tradeoff between time and return in zero-coupon bonds.

Practical Applications

Zero-coupon bonds are often used as benchmarks for risk-free rates in financial modeling, especially government-issued bonds like U.S. Treasury STRIPS. Their predictable returns make them attractive for long-term financial planning, such as retirement savings or funding specific future liabilities. Additionally, they are favored for their simplicity in calculating returns and for eliminating reinvestment risk since no interim payments are made.

6.2.3 Risk-Free Interest Rates

Risk-free interest rates represent the theoretical return on an investment with no risk of financial loss. In practice, government-issued zero-coupon bonds, such as U.S. Treasury bonds, are often used as proxies for risk-free rates due to their high creditworthiness and negligible default risk.

Why Use Zero-Coupon Bonds as Benchmarks?

1. 1. No Reinvestment Risk: Zero-coupon bonds do not make interim payments, avoiding the uncertainty of reinvesting coupons at fluctuating rates.
   2. Simplicity: Their pricing structure, based solely on the face value and time to maturity, provides a straightforward measure of interest rates for a given time horizon.
   3. Government Backing: Treasury zero-coupon bonds are considered virtually risk-free, making them reliable for financial models and comparisons.

The Role of Risk-Free Rates in Finance

Risk-free rates are foundational in financial calculations and decision-making. They:

• • Serve as the starting point for pricing other securities by adding risk premiums.
  • Help assess opportunity costs in capital budgeting and investment appraisals.
  • Determine the cost of equity in models like the Capital Asset Pricing Model (CAPM).

Challenges in Estimating Risk-Free Rates

1. 1. 1. Inflation Expectations: Nominal risk-free rates reflect anticipated inflation, making it important to adjust for real returns in long-term analyses.
      2. Currency and Country Risk: In global finance, different governments have varying credit standings, leading to multiple benchmarks for “risk-free” rates.

Key Insight

The risk-free rate sets the baseline for evaluating all financial assets. Whether in valuing investments, pricing bonds, or determining discount rates, understanding and applying this concept is crucial for informed decision-making.

6.3 Coupon Bonds

6.3.1 Coupon Bond Cash Flows

Concept Overview

Coupon bonds are a type of debt security where the issuer makes periodic interest payments (called coupon payments) to the bondholder until the bond matures. At maturity, the bondholder also receives the face value (principal) of the bond. Coupon bonds are widely used by corporations, governments, and other entities to raise capital.

Key Features

1. 1. 1. Coupon Payments: Regular payments based on the bond’s coupon rate, calculated as a percentage of the bond’s face value.
      2. Maturity Date: The date on which the bond’s face value is repaid to the bondholder.
      3. Face Value (Principal): The amount repaid at maturity, typically $1,000 per bond.

Formula for Coupon Payment

[latex]\text{Coupon Payment (CPN)} = \frac{\text{Coupon Rate} \times \text{Face Value}}{\text{Number of Payments per Year}}[/latex]

6.3.2 Yield to Maturity (YTM) of a Coupon Bond

Concept Overview

The yield to maturity (YTM) represents the total return an investor earns if the bond is held until maturity, considering both coupon payments and any capital gain or loss due to the bond’s purchase price. YTM is expressed as an annualized percentage rate.

YTM Formula

Finding the YTM requires solving the following equation for YTM, where C is the annual coupon payment, P is the current price, F is the face value, and N is the number of years to maturity.

$$P = \frac{C}{(1 + YTM)^1} + \frac{C}{(1 + YTM)^2} + … + \frac{C + F}{(1 + YTM)^N}$$

Where:

• • P = Current Price of the Bond
  • t = Time Period
  • n = Number of Periods until Maturity
  • r = YTM (to be solved for)

6.3.3 Coupon Bond Price Quotes

Concept Overview

Bond prices are commonly quoted as a percentage of their face value. A bond trading at par has a quoted price of 100, meaning its price is equal to its face value. Bonds trading at a premium (above par) or a discount (below par) have quoted prices above or below 100, respectively.

Formula for Bond Price from Quote

[latex]\text{Price} = \text{Face Value} \times \frac{\text{Quoted Price}}{100}[/latex]

Interpreting Bond Quotes in the Market

Bond price quotes reflect current market demand and interest rates. Several factors influence whether a bond trades at a premium or discount:

1. Coupon Rate vs. Market Rate:

•If the bond’s coupon rate is higher than prevailing market rates, it trades at a premium.

•If the bond’s coupon rate is lower than market rates, it trades at a discount.

2. Issuer Credit Risk: Bonds from issuers with strong credit ratings may trade at premiums due to perceived safety, while those with weaker credit ratings may trade at discounts.

3. Time to Maturity: Shorter-term bonds tend to have prices closer to par, while long-term bonds may show greater premiums or discounts depending on interest rate changes.

Investor Decision:

The investor considers their risk tolerance and investment goals:

• • If they prefer stability and shorter time horizons, Bond A is more suitable despite its premium price.
  • If they are comfortable with greater interest rate risk for potentially higher returns (via yield to maturity), Bond B might be the better choice.

6.4 Why Bond Prices Change

6.4.1. Interest Rate Changes and Bond Prices

Concept Overview

Bond prices and interest rates have an inverse relationship:

• • When interest rates rise, bond prices fall.
  • When interest rates fall, bond prices rise.

This occurs because newly issued bonds reflect the current market rate, making older bonds with lower coupon rates less attractive, leading to a price decrease. Conversely, older bonds with higher coupon rates become more desirable when rates drop, increasing their prices.

Formula for Bond Price

The price of a bond is the present value of its future cash flows (coupon payments and face value), discounted at the market interest rate (r):

$$\text{Bond Price} = \sum_{t=1}^{n} \frac{\text{Coupon Payment}}{(1 + r)^t} + \frac{\text{Face Value}}{(1 + r)^n}$$

6.4.2. Time to Maturity and Bond Prices

Concept Explanation

The time to maturity affects a bond’s price sensitivity to interest rate changes. Long-term bonds are more sensitive to interest rate fluctuations than short-term bonds, a phenomenon quantified by duration.

Duration

Duration measures a bond’s sensitivity to interest rate changes, expressed in years. Modified duration adjusts duration to account for yield to maturity.

Formula for Price Change Using Modified Duration

[latex]\text{Price Change (\%)} \approx -\text{Modified Duration} \times \text{Change in Interest Rate}[/latex]

6.4.3. Interest Rate Risk and Bond Prices

Concept Overview

Interest rate risk refers to the potential for bond prices to fluctuate due to changes in interest rates. Bonds with longer maturities or lower coupon rates are more sensitive to interest rate changes, leading to greater price volatility. Investors managing portfolios must carefully balance interest rate risk based on their investment horizon and risk tolerance.

6.4.5 Callable Bonds

A callable bond is a bond that allows the issuer to redeem it before the scheduled maturity date at a predetermined price, known as the call price. This feature gives issuers flexibility to refinance debt if interest rates drop, but it introduces reinvestment risk for bondholders, who may not be able to reinvest at the same return.

How Callable Bonds Work

When an issuer calls a bond, they typically pay bondholders the face value plus a premium, known as the call premium. For example, if a bond with a face value of $1,000 is called at a call price of $1,050, the bondholder will receive $1,050. Callable bonds usually offer higher coupon rates to compensate for the risk of early redemption.

Key Terms

• • Call Price: The amount the issuer pays to call the bond, usually higher than the face value.
  • Call Date: The first date the bond can be called by the issuer.
  • Call Protection Period: A period during which the bond cannot be called.
  • Yield to Call (YTC): The return an investor earns if the bond is called before maturity.
  • Why Issuers Call Bonds

Issuers call bonds to save on interest payments. If market interest rates fall, they can call their existing bonds and issue new bonds at lower rates. This reduces their cost of borrowing.

Risks for Investors

Callable bonds introduce reinvestment risk. If a bond is called when interest rates are lower, bondholders may have to reinvest the proceeds at a lower return. This makes callable bonds less attractive compared to non-callable bonds.

Example of Reinvestment Risk:

• • A $1,000 callable bond pays a 5% coupon and matures in 10 years. The bond is callable after 5 years at a call price of $1,050.
  • If the bond is called after 5 years, the bondholder receives $1,050 but must now reinvest at prevailing lower rates.

Formula for Yield to Call (YTC)

The YTC formula is similar to the YTM formula, but it assumes the bond is called on the call date instead of held to maturity.

YTC Formula:

YTC ≈ (Annual Coupon Payment + (Call Price – Current Price) / Years to Call) / ((Call Price + Current Price) / 2)

Where:

• • Annual Coupon Payment = Face Value × Coupon Rate
  • Call Price = Price at which the bond is redeemed early
  • Current Price = Price paid for the bond
  • Years to Call = Time until the bond can be called

Final Notes for Problem-Solving

• • YTC is only relevant if the bond is expected to be called. If the bond is unlikely to be called, use YTM instead.
  • Investors should compare YTM and YTC to decide if the bond is worth investing in.

6.5 Corporate Bonds

6.5.1. Credit Risk

Corporate bonds differ from government bonds primarily because they carry credit risk—the risk that the issuing company may default on interest or principal payments. The level of credit risk depends on the financial stability and creditworthiness of the issuing company.

Measuring Credit Risk

• Credit Ratings: Agencies like Moody’s, S&P, and Fitch assign credit ratings to corporate bonds based on the issuer’s creditworthiness. Ratings range from investment-grade (AAA to BBB) to speculative-grade or “junk bonds” (BB and below).
• Credit Spread: The difference in yield between a corporate bond and a risk-free government bond of similar maturity compensates investors for the additional risk.

6.5.2. Corporate Bond Yields

Concept Explanation

The yield on a corporate bond represents the return an investor expects to earn. This yield incorporates the bond’s coupon payments, the price paid, and the time until maturity.

Types of Yields

• • Current Yield: The bond’s annual coupon payment divided by its market price:

$$\text{Current Yield} = \frac{\text{Coupon Payment}}{\text{Bond Price}}$$

• • Yield to Maturity (YTM): The total return expected if the bond is held to maturity. YTM considers both coupon payments and capital gains or losses.

6.5.3. Bond Ratings

Bond ratings, assigned by agencies like Moody’s, S&P, and Fitch, assess the creditworthiness of a corporate bond issuer. These ratings reflect the likelihood of the issuer defaulting on payments and significantly influence the bond’s yield and price. They help investors gauge the risk associated with a particular bond.

Rating Scales

1. Investment-Grade Bonds:

• • AAA to BBB: Bonds with a high probability of repayment and low risk of default.

Example: Bonds issued by blue-chip companies or stable corporations.

2. Speculative-Grade (High-Yield or Junk) Bonds:

• • BB and Below: Bonds with a higher risk of default but offering higher yields to compensate investors.

Example: Bonds from smaller or financially weaker companies with uncertain credit stability.

How Ratings Influence Bonds

• • Higher Ratings (AAA, AA): Lower yields due to lower risk.
  • Lower Ratings (BB, B, CCC): Higher yields to attract investors willing to take on greater risk.

6.5.4. Corporate Yield Curves

Concept Explanation

The corporate yield curve illustrates the relationship between bond yields and their maturities for corporate issuers. Unlike the Treasury yield curve, which reflects risk-free rates, the corporate yield curve incorporates credit risk and liquidity factors, making it a valuable tool for analyzing corporate bonds.

Factors Influencing the Corporate Yield Curve

1. 1. Credit Quality:

• • Higher-rated bonds (e.g., AAA) have lower yield curves due to lower default risk.
  • Lower-rated bonds (e.g., BB) exhibit higher yield curves to compensate for increased credit risk.

1. 2. Economic Conditions:

• • During economic downturns, yield curves often steepen as long-term bonds carry higher yields to reflect elevated risk over time.

1. 3. Market Sentiment:

• • Investor confidence or caution impacts demand for short- or long-term bonds, influencing the shape of the yield curve.

Key Observations

• • Steep Yield Curve: Reflects higher perceived risk or expectations of rising interest rates.
  • Flat Yield Curve: Suggests stability or economic uncertainty, with minimal differences in yields across maturities.
  • Inverted Yield Curve: May indicate economic recession expectations, as short-term yields exceed long-term yields