3 Chapter 3 – Time value of Money
Learning Objectives
- Understand the foundational principle of the Time Value of Money (TVM) and its importance in financial decision-making.
- Learn how to calculate the Future Value (FV) of a single cash flow using compound interest.
- Learn how to calculate the Present Value (PV) of a single future cash flow by applying the discounting process.
- Explore the relationship between interest rates, time, and the value of cash flows.
- Apply TVM concepts to real-life scenarios, such as savings, investment decisions, and evaluating loan offers.
3.1 Introduction to Time Value of Money (TVM)
3.1.1 What is Time Value of Money?
The Time Value of Money (TVM) is a cornerstone of finance. It states that money today is worth more than the same amount in the future due to its earning potential. This principle allows businesses and individuals to evaluate investments, loans, and financial plans effectively. TVM is crucial for sound financial decision-making.
3.1.2 Why Does Money Have Time Value?
Would you prefer to receive $1,000 today or a year from now? Most people would choose today’s $1,000 because it can be invested to grow over time. For example, depositing $1,000 in an account earning 5% annual interest would grow to $1,050 in one year. This growth illustrates the Time Value of Money (TVM)—money today has greater earning power than in the future.
3.1.3 How Is TVM Used in Real Life?
TVM isn’t just a theory; it’s part of daily financial decisions. Here are a few practical examples:
• Personal Savings: When you deposit money in a savings account, you earn interest. This interest makes the money you deposit today worth more in the future.
• Loans and Mortgages: When borrowing money, lenders consider TVM to determine the interest rates they charge. Higher interest rates reflect the lender’s expectation that the value of money will decrease over time.
• Investment Decisions: Companies use TVM to evaluate projects and investments. They compare the present value of cash inflows and outflows to decide if an investment is worthwhile.
Beyond personal finance, the Time Value of Money is critical in corporate decision-making. Companies assess projects, evaluate investment opportunities, and make capital allocation decisions based on TVM principles. For example:
•Supply Chain Contracts: A supplier offering deferred payment terms may charge more to account for the time value of money.
•Lease or Buy Decisions: Businesses analyze the present value of lease payments versus an upfront purchase cost to decide the most cost-effective option.
For example, Suppose you’re deciding between taking a lump sum of $10,000 today or receiving $1,200 annually for the next 10 years. Using TVM, you could calculate the present value of the yearly payments and compare it to the $10,000 to make an informed choice.
3.2 Future Value Concepts
Understanding Future Value (FV) Future Value (FV) represents how much a sum of money today will be worth at a future date, considering the interest it earns over time. It’s essential in financial planning, investment decisions, and assessing the long-term value of saving. Future value calculations help determine the growth potential of investments, from savings accounts to bonds and stocks.
The Basics of Compound Interest Compound interest is a key concept in calculating future value. Unlike simple interest, which earns interest only on the original principal, compound interest earns interest on both the principal and accumulated interest over time. The formula for calculating FV with compound interest is:
Formula for Future Value with Compound Interest:
$$
FV = PV \times (1 + r)^n
$$
Where:
• FV = Future Value
• PV = Present Value (initial investment)
• r = Interest rate (as a decimal)
• n = Number of compounding periods
Example: How Compound Interest Works Over Time
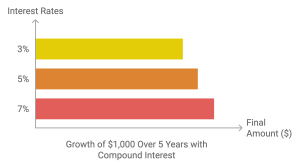
Let’s explore how an investment of $1,000 at a 5% annual interest rate grows over 5 years when compounded annually.
•Year 1:
$$FV = 1,000 \times (1 + 0.05)^1 = 1,050$$
After the first year, your investment grows by $50 in interest, resulting in $1,050.
•Year 2:
[latex]FV = 1,000 \times (1 + 0.05)^2 = 1,102.50[/latex]
In the second year, interest is earned on both the original $1,000 and the $50 from Year 1, adding another $52.50, bringing the total to $1,102.50.
•Year 3:
[latex]FV = 1,000 \times (1 + 0.05)^3 = 1,157.63[/latex]
By the third year, the interest earned grows to $55.13, further boosting the total to $1,157.63.
•Year 4:
[latex]FV = 1,000 \times (1 + 0.05)^4 = 1,215.51[/latex]
The interest earned in Year 4 is $57.88, increasing the total to $1,215.51.
•Year 5:
[latex]FV = 1,000 \times (1 + 0.05)^5 = 1,276.28[/latex]
Finally, in Year 5, the interest earned is $60.77, bringing the total future value to $1,276.28.
Key insights from This Example:
- The Power of Compounding: Interest is earned not only on the principal but also on accumulated interest, resulting in exponential growth over time.
- Patience Pays Off: The longer your money stays invested, the more pronounced the effect of compounding becomes.
- Visualizing Growth: Over 5 years, the total interest earned adds up to $276.28, or 27.6% of the original $1,000 investment.
Interactive Question for Students:
•How much would your investment grow to in 10 years instead of 5 years at the same rate? Use the formula:
[latex]FV = 1,000 \times (1 + 0.05)^{10}[/latex]
Applications of Future Value Future value calculations are used in various real-world scenarios:
• Savings Goals: Planning for a large purchase or retirement requires knowing how much an investment will grow.
• Investment Comparisons: Investors use FV to compare potential returns from different investment options.
• Loans and Debts: Understanding how much debt grows over time helps borrowers make better repayment decisions.
3.3 Present Value and Discounting Cash Flows
3.3.1 What is Present Value (PV)?
Present Value (PV) is a fundamental concept in finance that represents the current worth of a future sum of money or stream of cash flows, given a specified rate of return. In essence, it answers the question: "How much is a future payment or series of payments worth right now?" This concept is crucial for making informed financial decisions, as it allows for the comparison of cash flows occurring at different times on an equal basis.
The calculation of Present Value involves discounting future cash flows back to the present using a specific interest rate, often referred to as the discount rate. This rate typically reflects the time value of money and the inherent risk associated with receiving the future cash flows. The higher the discount rate, the lower the present value, reflecting the increased risk or opportunity cost associated with waiting for future payments.
Formula for Present Value:
$$ PV = \frac{FV}{(1 + r)^n} $$
Where:
PV = Present Value
FV = Future Value (amount to be received in the future)
r = Interest rate (as a decimal)
n = Number of periods until payment
Example: Calculating Present Value
Suppose you want to have $1,000 in 5 years, and the annual interest rate is 5%, compounded annually. How much should you invest today to achieve that goal?
Step-by-Step Calculation
To calculate Present Value (PV), use the formula:
$$ PV = \frac{FV}{(1 + r)^n} $$
Where:
•FV = 1,000 (Future Value you want in 5 years)
•r = 0.05 (Annual interest rate as a decimal)
•n = 5 (Number of years)
1. Substitute the Values:
$$ PV = \frac{1,000}{(1 + 0.05)^5} $$
2. Calculate the Denominator:
$$(1 + 0.05)^5 = 1.27628$$
3. Divide to Find PV:
$$ PV = \frac{1,000}{1.27628} \approx 783.53 $$
Result
You need to invest $783.53 today to have $1,000 in 5 years at an annual interest rate of 5%.
What Happens with a Different Interest Rate?
If the interest rate is 10% instead of 5%, the PV changes:
1. Recalculate Denominator:
$$(1 + 0.10)^5 = 1.61051 $$
2. Divide to Find PV:
[latex]PV = \frac{1,000}{1.61051} \approx 620.92[/latex]
With a 10% interest rate, you only need to invest $620.92 today to reach $1,000 in 5 years.
Key Insights from This Example
1. The Impact of Discounting:
•Future cash flows are “discounted” to account for the time value of money.
•Money today is worth more because it can earn interest over time.
2. Understanding Present Value:
•PV tells you how much you need to invest now to achieve a future goal.
•The higher the interest rate or the longer the time, the smaller the PV for the same future value.
Examples: Real-World Applications
1. Saving for a Goal:
You’re planning a purchase that will cost $1,000 in 3 years, and you can earn 4% annual interest on your savings. How much should you save today?
• Use FV = 1,000, r = 0.04, n = 3:
$$PV = \frac{1,000}{(1 + 0.04)^3} = \frac{1,000}{1.12486} \approx 889.00$$
You need to save $889.00 today.
2. Paying Off Debt:
You owe $1,000 in 2 years, and the lender offers to accept an early payment at a 6% discount rate. How much do you need to pay today?
• Use FV = 1,000, r = 0.06, n = 2:
$$PV = \frac{1,000}{(1 + 0.06)^2} = \frac{1,000}{1.1236} \approx 890.00$$
You’d need to pay $890.00 today.
Interactive Question for Students
•If you want $1,000 in 10 years, and the annual interest rate is 8%, how much should you invest today?
•Use the formula:
$$PV = \frac{FV}{(1 + r)^n}$$
3.3.2 PV is an essential tool for various financial applications:
-
- Investment Analysis: Investors use PV to determine whether a potential investment is worthwhile by comparing its cost to the present value of its expected future returns.
- Capital Budgeting: Businesses employ PV calculations to evaluate and compare different investment projects, helping them allocate resources efficiently.
- Loan Evaluation: Both lenders and borrowers use PV to assess the true cost of loans and to compare different loan offers.
- Asset Valuation: Financial analysts use PV techniques to value assets, particularly those that generate cash flows over time, such as bonds or real estate investments.
The concept of PV is intrinsically linked to the time value of money principle, which posits that a dollar today is worth more than a dollar in the future. This is due to several factors:
-
- Opportunity Cost: Money available now can be invested to generate returns, an opportunity lost if receiving the money is delayed.
- Inflation: The purchasing power of money typically decreases over time due to inflation, making future dollars less valuable.
- Risk: There's always some level of uncertainty associated with future cash flows, which is accounted for in the discount rate.
Understanding and applying the concept of Present Value is crucial for anyone involved in financial decision-making, from individual investors planning for retirement to corporate finance professionals evaluating multi-million dollar projects. By providing a way to compare and analyze cash flows occurring at different times, PV serves as a cornerstone of modern financial analysis and decision-making processes.
3.3.3 Why is Present Value Important? PV is a critical concept in finance for several reasons:
-
Evaluating Investments: Present Value helps investors decide if an investment is worthwhile by comparing its current cost to what it might be worth in the future.Making Loan Decisions: When borrowing money, Present Value can show whether it's better to pay a lump sum now or spread payments over time.Planning Business Projects: Companies use Present Value to look at future cash flows from different projects. This helps them choose which investments will make the most money.
3.4 Non-Annual Compounding and Effective Rates
3.4.1 What is Non-Annual Compounding?
Non-annual compounding occurs when interest is calculated and added to the principal more frequently than once a year. Examples include monthly, quarterly, or daily compounding. Non-annual compounding affects both the Future Value (FV) and the Effective Annual Rate (EAR) of an investment or loan.
Formula for Future Value with Non-Annual Compounding:
[latex]FV = PV \times \left(1 + \frac{r}{m}\right)^{n \times m}[/latex]
Where:
• PV = Present Value
• r = Annual interest rate (as a decimal)
• m = Number of compounding periods per year (e.g., 12 for monthly)
• n = Number of years
Example: Monthly Compounding for an Investment
Scenario
You invest $5,000 in a savings account that offers an 8% annual interest rate, compounded monthly. You plan to leave the money untouched for 3 years. What will the Future Value (FV) of your investment be after 3 years?
Step-by-Step Calculation
The formula for Future Value (FV) with non-annual compounding is:
[latex]FV = PV \times \left(1 + \frac{r}{m}\right)^{n \times m}[/latex]
Where:
•PV = 5,000 (Present Value or initial investment)
•r = 0.08 (Annual interest rate as a decimal)
•m = 12 (Number of compounding periods per year, monthly compounding)
•n = 3 (Number of years)
1. Calculate the Monthly Interest Rate (r/m):
[latex]\text{Monthly Interest Rate} = \frac{0.08}{12} = 0.0066667[/latex]
2. Determine the Total Number of Compounding Periods (n \times m):
[latex]\text{Total Periods} = 3 \times 12 = 36[/latex]
3. Substitute the Values into the FV Formula:
[latex]FV = 5,000 \times \left(1 + 0.0066667\right)^{36}[/latex]
[latex]FV = 5,000 \times (1.0066667)^{36}[/latex]
4. Raise the Base to the Power of 36:
Using a calculator or software:
[latex](1.0066667)^{36} \approx 1.28368[/latex]
5. Multiply by the Present Value (PV):
[latex]FV = 5,000 \times 1.28368 \approx 6,418.40[/latex]
Result
After 3 years, your investment will grow to approximately $6,418.40.
Key Takeaways
1. Impact of Monthly Compounding:
•Compared to annual compounding, monthly compounding earns more interest because interest is calculated and added to the principal 12 times per year instead of once.
•With annual compounding at 8%, the FV would have been $6,299.86 (less than monthly compounding).
2. Frequent Compounding Means Faster Growth:
•The more frequent the compounding, the faster the investment grows. Daily compounding would result in an even higher FV.
Follow-Up Question for Students
How would the Future Value change if the same investment were compounded daily instead of monthly?
•Use m = 365 and follow the same steps to calculate FV.
3.4.2 Effective Annual Rate (EAR)
The Effective Annual Rate (EAR) converts a nominal interest rate with non-annual compounding into an annualized rate. This allows for better comparisons between investments or loans with different compounding frequencies.
Formula for EAR:
[latex]EAR = \left(1 + \frac{r}{m}\right)^m - 1[/latex]
Where:
• r = Nominal interest rate (as a decimal)
• m = Number of compounding periods per year
Example: EAR for Monthly Compounding
Scenario:
An account offers an 8% annual nominal interest rate, compounded monthly. What is the EAR?
1. Identify variables:
[latex]r = 0.08, \, m = 12[/latex]
2. Substitute into the formula:
[latex]EAR = \left(1 + \frac{0.08}{12}\right)^{12} - 1[/latex]
3. Calculate monthly interest rate:
[latex]\frac{0.08}{12} = 0.0066667[/latex]
4. Solve for EAR:
[latex]EAR = \left(1.0066667\right)^{12} - 1 \approx 0.083 = 8.3\%[/latex]
Result:
An 8% nominal interest rate, compounded monthly, is equivalent to an 8.3% EAR.
Why Is EAR Important? Understanding EAR helps in making better financial decisions:
• Comparing Loan Offers: Borrowers can use EAR to see which loan is more cost-effective, even if they have different compounding frequencies.
• Investment Choices: Investors can determine which savings or investment accounts offer the best return after accounting for how often interest is compounded.
Case Study: Comparing Investment Accounts
Background:
Mark, a recent college graduate, has started a new job and wants to invest his savings in an account that offers the best return. He has narrowed down his options to two banks, each offering different interest rates and compounding frequencies:
-
- Bank A offers an annual interest rate of 8%, compounded quarterly.
- Bank B offers an annual interest rate of 7.9%, compounded monthly.
Mark needs to determine which bank account will give him the highest effective return over the course of a year.
Objective:
Students will use the formulas for Future Value with Non-Annual Compounding and Effective Annual Rate (EAR) to analyze Mark’s options and decide which bank account is more beneficial.
Task:
- Calculate the Effective Annual Rate (EAR) for each bank account:
- Bank A: 8% compounded quarterly.
- Bank B: 7.9% compounded monthly.
- Determine which bank account provides the highest effective annual rate and explain why it would be the better investment for Mark.
Formulas:
[latex]EAR = \left(1 + \frac{r}{m}\right)^m - 1[/latex]
Calculation:
Bank A (8% compounded quarterly):
r = 0.08
m = 4
[latex]EAR = \left(1 + \frac{0.08}{4}\right)^4 - 1 \approx 8.24\%[/latex]
Bank B (7.9% compounded monthly):
r = 0.079
m = 12
[latex]EAR = \left(1 + \frac{0.079}{12}\right)^{12} - 1 \approx 8.17\%[/latex]
Questions for Discussion:
- Based on the EAR calculations, which bank should Mark choose?
- Why is the EAR important when comparing investment or loan offers?
- How would the decision change if the compounding frequency at Bank B were increased to daily?
Reference:
To explore the importance of compounding frequency and interest rates, students can refer to Investopedia’s article on Effective Annual Rate.
Exercises
Real-Life Application: Consider a scenario where two banks offer different savings account options:
• Bank A offers a 6.5% interest rate, compounded quarterly.
• Bank B offers a 6.3% interest rate, compounded daily.
Calculating the EAR for each option allows you to determine which bank is actually offering a better return on your money.
3.5 Applying Time Value of Money in Business and Personal Finance
Why Time Value of Money (TVM) Matters in Real Life
The concept of Time Value of Money (TVM) goes beyond theory—it’s a practical tool that helps individuals and businesses make sound financial decisions. From saving for retirement to choosing the right investment or loan, TVM principles guide critical decisions that shape financial futures.
Examples in Personal Finance
1. Retirement Planning:
Starting early with small, consistent investments can lead to substantial savings over time, thanks to the power of compound interest.
•Example:
If you contribute $200 per month to a retirement account earning 6% annual interest (compounded monthly) for 30 years, how much will you save?
$$FV = PMT \times \frac{\left(1 + \frac{r}{m}\right)^{n \times m} - 1}{\frac{r}{m}}$$
Where:
- PMT = 200
- r = 0.06, m = 12, n = 30
$$FV = 200 \times \frac{\left(1 + \frac{0.06}{12}\right)^{12 \times 30} - 1}{\frac{0.06}{12}}$$
$$FV = 200 \times \frac{(1.005)^360 - 1}{0.005} \approx 200 \times \frac{6.022575 - 1}{0.005}$$
$$FV \approx 200 \times 1,004.52 \approx 200,904$$
You will accumulate approximately $200,904 over 30 years, illustrating the importance of starting early.
2. Loan Comparisons:
Understanding TVM helps in comparing loan options to choose the one with the lowest effective cost.
•Example:
A fixed-rate mortgage with a lower monthly payment might appear attractive, but factoring in total interest paid over the loan’s life using PV calculations provides a clearer picture.
Examples in Business Finance
1. Investment Decisions:
Businesses rely on TVM to assess whether projects or investments will add value to the firm.
•Example:
A company evaluates purchasing new machinery costing $100,000, which will generate $30,000 annually for 5 years. If the discount rate is 8%, the Present Value (PV) of cash inflows can be calculated to determine if the investment is worthwhile.
$$PV = \sum \frac{CF_t}{(1 + r)^t}$$
Where:
- CF_t = 30,000, r = 0.08, t = 1 to 5
- $$PV = \frac{30,000}{1.08^1} + \frac{30,000}{1.08^2} + \frac{30,000}{1.08^3} + \frac{30,000}{1.08^4} + \frac{30,000}{1.08^5}$$
- $$PV \approx 27,778 + 25,720 + 23,815 + 22,059 + 20,425 \approx 119,797$$
Since the PV of cash inflows (119,797) exceeds the cost (100,000), the investment adds value to the company.
2. Capital Budgeting:
Small business owners often use TVM to decide between immediate and deferred investments.
•Example:
Should a company buy new software for $20,000 today or wait two years for an improved version costing $22,000? Assuming a 5% discount rate, calculate the PV of the future cost:
$$PV = \frac{FV}{(1 + r)^n}$$
$$PV = \frac{22,000}{(1 + 0.05)^2} \approx \frac{22,000}{1.1025} \approx 19,951$$
Since the PV of the future cost is slightly less than $20,000, it may be worth waiting, especially if the improved software provides added value.
Case Study: A Real Estate Investor’s Dilemma
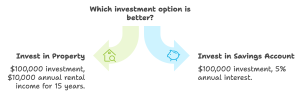
Scenario:
A real estate investor has two options:
- Invest $150,000 in a rental property, expecting annual cash flows of $20,000 for 10 years.
- Deposit $150,000 in a savings account earning 6% annual interest.
Analysis:
- Option 1 (Rental Property):
Using PV calculations with a discount rate of 6%:
$$PV = \sum \frac{20,000}{(1 + 0.06)^t} \, \text{for } t = 1 \text{ to } 10$$
$$PV \approx 18,868 + 17,799 + 16,792 + \ldots + 11,167 \approx 147,200$$
- Option 2 (Savings Account):
Using FV calculations:
$$FV = 150,000 \times (1 + 0.06)^{10} \approx 150,000 \times 1.7908 \approx 268,620$$
- Conclusion:
Although the rental property offers steady cash flows, the savings account provides a higher value over the same period, assuming consistent growth and no major market risks.
Interactive Exercise
Question:
You win a lottery and can choose between:
-
-
- $500,000 today
- $600,000 in 5 years
-
Assume an annual discount rate of 6%. Which option is better? Use PV calculations to decide.
Key Takeaways
- Time Value of Money (TVM): Money today is worth more than the same amount in the future because it can be invested to earn interest.
- Future Value (FV): Represents the growth of a sum of money over time through compound interest.
- Present Value (PV): Represents the current worth of a future cash flow, discounted for the time value of money.
- Interest Rates: Higher interest rates increase future value but reduce present value.
- Practical Applications: TVM is used in personal savings, investment evaluations, and loan comparisons, forming the basis for sound financial decisions.
Exercises
Conceptual Questions
1. Why is Money Today Worth More?
Explain why $1,000 today is worth more than $1,000 received in the future. What factors contribute to the time value of money?
2. Future Value and Compounding
Why does compounding lead to exponential growth? How does the frequency of compounding impact the future value of an investment?
3. Present Value and Discounting
Why does an increase in the discount rate reduce the present value of future cash flows?
4. Applications of TVM
Provide two examples of how businesses or individuals use time value of money concepts in everyday decision-making.
Short Calculations
1. Simple Future Value Calculation
You invest $2,000 in an account earning 6% annual interest, compounded annually. What will the investment be worth in 4 years?
2. Present Value of a Future Sum
If you want $5,000 in 10 years and can invest at 8% annual interest, how much do you need to invest today?
3. Future Value with Non-Annual Compounding
A savings account offers 5% annual interest, compounded monthly. If you deposit $3,000 today, what will it be worth in 6 years?
4. Effective Annual Rate (EAR)
A loan has a nominal interest rate of 10%, compounded quarterly. What is the EAR?
Scenario-Based Problems
1. Comparing Investment Options
You have two investment options:
-
- Option A: $10,000 invested at 5% annual interest, compounded yearly, for 8 years.
- Option B: $10,000 invested at 4.8% annual interest, compounded monthly, for 8 years.
Which option provides the higher future value?
2. Retirement Planning
You plan to save $500 per month for 30 years in an account earning 7% annual interest, compounded monthly. What will your savings be worth at the end of 30 years?
3. Loan Decisions
You borrow $50,000 at a nominal annual interest rate of 6%, compounded monthly. The loan term is 5 years.
-
- What is the total amount of interest paid over the life of the loan?
- What is the effective annual rate (EAR) for the loan?
Case Study: Lump Sum vs. Annuity
Scenario:
You’ve won a lottery with the following payout options:
•Option A: $500,000 today.
•Option B: $50,000 annually for 15 years.
Task:
If the discount rate is 6%, calculate the present value of the annual payments under Option B using the formula for discounting multiple cash flows:
$$PV = \sum_{t=1}^{n} \frac{CF_t}{(1 + r)^t} $$
Discussion:
Which option would you choose, based on the present value? Briefly explain your reasoning.
Note: We will explore annuities and their specific formulas in Chapter 5 for more structured cash flow streams.
Interactive Challenge
Question:
You need $100,000 in 8 years to fund a down payment for a house. You have two options:
-
- Invest $75,000 today in an account earning 4% annual interest.
- Contribute $800 monthly to a savings account earning 6% annual interest, compounded monthly.
-
- Calculate the future value of both options.
- Which option meets your goal, and which is more cost-effective?