Í þessum kafla er farið í fylkjajöfnur, lausn línulegra jöfnuhneppa og jöfnu bestu línu í gegnum punktasafn.

Fylkjajöfnur

Hér verða teknar fyrir fylkjajöfnurnar

[latex]AX=B[/latex] og [latex]YA=B[/latex]

þar sem [latex]A[/latex] og [latex]B[/latex] eru gefin [latex]2 \times 2[/latex] fylki, en [latex]X[/latex] og [latex]Y[/latex] eru óþekkt [latex]2 \times 2[/latex] fylki.

Forsenda þess að hægt sé að leysa fylkjajöfnur af þessu tagi er að [latex]A[/latex] eigi sér andhverfu, það er að [latex]A^{-1}[/latex] sé til.

Tökum fyrst fyrri jöfnuna, [latex]AX=B[/latex], og margföldum frá vinstri báðum megin við samasem merkið með [latex]A^{-1}[/latex] og notfærum að [latex]A^{-1}A =I[/latex] og [latex]IX=X[/latex]. Þá fæst

[latex]A^{-1}AX = A^{-1}B[/latex]
[latex]IX = A^{-1}B[/latex]
[latex]X = A^{-1}B[/latex]

Hér þarf að athuga að forsenda fyrir [latex]A^{-1}A =I[/latex] er að [latex]A^{-1}[/latex] og [latex]A[/latex] liggi saman, annað fylki má ekki koma upp á milli þeirra.

Margföldum gegnum seinni jöfnuna, [latex]YA=B[/latex] með [latex]A^{-1}[/latex] frá hægri. Þá fæst

[latex]YAA^{-1} = BA^{-1}[/latex]
[latex]YI = BA^{-1}[/latex]
[latex]Y = BA^{-1}[/latex]

Í myndbandinu (7:17 mín.) hér fyrir neðan er farið í það hvernig fylkjajöfnur eru leystar og og tekið er eitt sýnidæmi:

https://youtu.be/zj7cKjHWjPU

Lausn:

[latex]det(A) = 7\cdot 9 - 4\cdot 16 =- 1[/latex]

[latex]A^{-1} =\frac{1}{-1} \begin{bmatrix} 9 & -4 \\ -16 & 7 \end{bmatrix} = \begin{bmatrix} -9 & 4 \\ 16 & -7 \end{bmatrix}[/latex]

Margföldum gegnum fyrri jöfnuna með [latex]A^{-1}[/latex] frá vinstri þá fæst

[latex]X = \begin{bmatrix} -9 & 4 \\ 16 & -7\end{bmatrix} \begin{bmatrix} 3 & 8 \\ 2 & 7 \end{bmatrix} = \begin{bmatrix} -19 & -44 \\ 34 & 79 \end{bmatrix}[/latex]

og margföldum gegnum fyrri jöfnuna með [latex]A^{-1}[/latex] frá hægri þá fæst

[latex]Y = \begin{bmatrix} 3 & 8 \\ 2 & 7 \end{bmatrix} \begin{bmatrix} -9 & 4 \\ 16 & -7 \end{bmatrix} = \begin{bmatrix} 101 & -44 \\ 94 & -41 \end{bmatrix}[/latex]

[latex]\square[/latex]

Línuleg jöfnuhneppi

Skoðum línulegt jöfnuhneppi með tveimur jöfnum og tveimur óþekktum stærðum [latex]x_1[/latex] og [latex]x_2[/latex] sem finna skal:

[latex]ax_1 + bx_2 = s[/latex]
[latex]cx_1 + dx_2 = t[/latex]

Stillum upp jöfnuhneppinu með fylkjum í eina fylkjajöfnu:

[latex]\begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} s \\ t \end{bmatrix}[/latex]

Fylkið [latex]A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}[/latex] kallast stuðlafylki.

Látum [latex]\vec{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}[/latex] og [latex]\vec{u} = \begin{bmatrix} s \\ t \end{bmatrix}[/latex]. Þá verður jafnan:

[latex]A \vec{x} = \vec{u}[/latex]

Nú er komin fylkjajafna sem leysist eins og í fylkjajöfnukaflanum hér að ofan.
Margföldum frá vinstri með [latex]A^{-1}[/latex], ef andhverfan er til, þá fæst

[latex]A^{-1} A \vec{x} = A^{-1} \vec{u}[/latex]
[latex]I \vec{x} = A^{-1} \vec{u}[/latex]
[latex]\vec{x} = A^{-1} \vec{u}[/latex]

Lausn:

Stillum upp fylkjajöfnu:

[latex]\begin{bmatrix} 11 & 8 \\ 9 & 7 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 13 \\ 29 \end{bmatrix}[/latex]

Látum [latex]A = \begin{bmatrix} 11 & 8 \\ 9 & 7 \end{bmatrix}[/latex], þá er [latex]det(A) = \frac{1}{11 \cdot 7 - 8 \cdot 9} = 5[/latex] svo [latex]A^{-1} = \frac {1}{5} \begin{bmatrix} 7 & -8 \\ -9 & 11 \end{bmatrix}[/latex]

Margföldum frá vinstri í gegnum fylkjajöfnuna með [latex]A^{-1}[/latex] og fáum

[latex]\begin{bmatrix} x \\ y \end{bmatrix} =\frac {1}{5} \begin{bmatrix} 7 & -8 \\ -9 & 11 \end{bmatrix} \begin{bmatrix} 13 \\ 29 \end{bmatrix}[/latex]

[latex]\begin{bmatrix} x \\ y \end{bmatrix} = \frac {1}{5} \begin{bmatrix} -141 \\ 202 \end{bmatrix}[/latex]

Því er [latex]x = - \frac{141}{5}[/latex] og [latex]y = \frac{202}{5}[/latex].

[latex]\square[/latex]

Þessa aðferð er hægt að nota fyrir stærri jöfnuhneppi. Hér er ekki farið í andhverfur stærri fylkja en [latex]2 \times 2[/latex] í höndunum, en það verður gert í tölvu Excel kaflanum og þar verður stærra jöfnuhneppi leyst. Það er hægt að leysa stærri jöfnuhneppi í höndunum með aðgerð sem kallast Gauss eyðing (e. Gaussian Elimination), sem ekki er tekin fyrir hér.

Jafna bestu línu

Í ýmsum hagnýtum verkefnum innan eðlisfræði, verkfræði, hagfræði og fleiri greinum þarf stundum að finna jöfnu bestu línu sem lýsir tilteknu punktasafni best.

Á myndinni hér fyrir neðan sést jafna bestu línu í gegnum safn tíu punkta: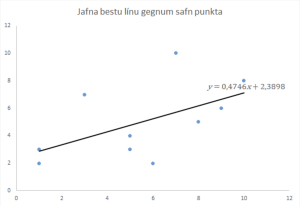Við höfum punktana [latex](x_1,y_1), (x_2,y_2), (x_3,y_3) \ldots (x_n,y_n)[/latex] og viljum finna jöfnu bestu línu, [latex]y = hx+q[/latex] sem gengur í gegnum þetta punktasafn.

Byrjum á að umrita línuna sem [latex]xh+q = y[/latex] og setjum punktana [latex](x_i, y_i)[/latex] inn. Þá fást [latex]n[/latex] jöfnur, ein fyrir hvert [latex]i[/latex]:

[latex]x_i h +q = y_i[/latex] fyrir [latex]i = 1,2,3,\ldots ,n[/latex]

Þetta kallast yfirákvarðað jöfnuhneppi.

Setjum upp í fylkjajöfnu

[latex]\begin{bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \\ \vdots & \vdots \\ x_n & 1 \end{bmatrix}\begin{bmatrix} h \\ q \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_n \end{bmatrix}[/latex]

Látum A= [latex]\begin{bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \\ \vdots & \vdots \\ x_n & 1 \end{bmatrix}[/latex], [latex]\vec{x} = \begin{bmatrix} h \\ q \end{bmatrix}[/latex] og [latex]\vec{y} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_n \end{bmatrix}[/latex].

Þá má skrifa

[latex]A \vec{x} = \vec{y}[/latex]

og finna þarf [latex]\vec{x}[/latex].

Nú er nausynleg forsenda að fylki sé ferningsfylki til að það geti átt sér andhverfu. Því margföldum við frá vinstri í gegnum fylkjajöfnuna með [latex]A[/latex] byltu, það er með [latex]A^T[/latex] frá vinstri:

[latex]A^T A \vec{x} = A^T \vec{y}[/latex]

Nú er fylkið [latex](A^T A)[/latex] [latex]2 \times 2[/latex] ferningsfylki.

Margföldum frá vinstri með [latex](A^T A)^{-1}[/latex] ef andhverfan er til

[latex](A^T A)^{-1}( A^T A) \vec{x} = (A^T A) ^{-1} A^T \vec{y}[/latex]
[latex]I \vec{x} = (A^T A)^{-1} A^T \vec{y}[/latex]
[latex]\vec{x} = (A^T A)^{-1} A^T \vec{y}[/latex]

Því er

[latex]\begin{bmatrix} h \\ q \end{bmatrix} = (A^T A)^{-1} A^T \vec{y}[/latex]

Lausn:

Jafna línu er [latex]y = hx + q[/latex]. Við þurfum að finna [latex]h[/latex] og [latex]q[/latex].
Umritum jöfnuna [latex]xh +q = y[/latex] og setjum punktana inn. Þá fæst fylkjajafnan

[latex]\begin{bmatrix} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ \end{bmatrix}\begin{bmatrix} h \\ q \end{bmatrix} = \begin{bmatrix} 1 \\ 5 \\ 2 \\ \end{bmatrix}[/latex]

Margföldum frá vinstri með byltu fylkinu sem er lengst til vinstri

[latex]\begin{bmatrix} 1 & 2 & 3 \\ 1 & 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 2 & 1 \\ 3 & 1 \\ \end{bmatrix}\begin{bmatrix} h \\ q \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 5 \\ 2 \\ \end{bmatrix}[/latex]

Einföldum, það er margföldum fylkin með tölunum saman og fáum

[latex]\begin{bmatrix} 14 & 6 \\ 6 & 3 \\ \end{bmatrix} \begin{bmatrix} h \\ q \end{bmatrix} = \begin{bmatrix} 17 \\ 8 \\ \end{bmatrix}[/latex]

Þá erum við komin með fylkjajöfnu sem leysist eins og gert er í fylkjajöfnu kaflanum hér ofar

[latex]\begin{bmatrix} h \\ q \end{bmatrix} = \frac{1}{14 \cdot3 - 6 \cdot 6} \begin{bmatrix} 3 & -6 \\ -6 & 14 \\ \end{bmatrix} \begin{bmatrix} 17 \\ 8 \\ \end{bmatrix} = \frac{1}{6}\begin{bmatrix} 3 \\ 10 \\ \end{bmatrix}[/latex]

Þannig að [latex]h = \frac {1}{2}[/latex] og [latex]q = \frac {5}{3}[/latex].  Því er jafna bestu línunnar [latex]y = \frac {1}{2} x + \frac {5}{3}[/latex].

[latex]\square[/latex]