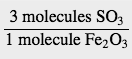Learning Objectives

By the end of this section, you will be able to:

  • Explain the concept of stoichiometry as it pertains to chemical reactions
  • Use balanced chemical equations to derive stoichiometric factors relating amounts of reactants and products
  • Perform stoichiometric calculations involving mass, moles, and solution molarity

A balanced chemical equation provides a great deal of information in a very succinct format. Chemical formulas provide the identities of the reactants and products involved in the chemical change, allowing classification of the reaction. Coefficients provide the relative numbers of these chemical species, allowing a quantitative assessment of the relationships between the amounts of substances consumed and produced by the reaction. These coefficients provide ratios between any reactants or products, and these ratios are helpful tools for understanding reactions.

Stoichiometry is a term derived from the Greek words stoicheion (meaning “element”) and metron (meaning “measure”). In this module we will explore stoichiometry, the use of balanced chemical equations and ratios of various components of those reactions.

 

The general approach to using stoichiometric relationships is similar in concept to the way people cook with recipes.

A recipe for making eight pancakes calls for 1 cup pancake mix, [latex]\frac{3}{4}[/latex] cup milk, and one egg. The “equation” representing the preparation of pancakes per this recipe is

[latex] 1 \;\text{cup mix} + \frac{3}{4} \;\text{cup milk} + 1 \;\text{egg} \longrightarrow 8 \;\text{pancakes}[/latex]

If two dozen pancakes are needed for a big family breakfast, the ingredient amounts must be increased proportionally according to the amounts given in the recipe. For example, the number of eggs required to make 24 pancakes is

[latex] 24 \;\rule[0.5ex]{4em}{0.1ex}\hspace{-4em}\text{pancakes} \times \frac{1 \;\text{egg}}{8 \;\rule[0.25ex]{3em}{0.1ex}\hspace{-3em}\text{pancakes}} = 3 \;\text{eggs}[/latex]

Balanced chemical equations are used in much the same fashion to determine the amount of one reactant required to react with a given amount of another reactant, or to yield a given amount of product. The coefficients in the balanced equation are used to derive stoichiometric ratios that permit computation of the desired quantity. The ratio is used as a conversion factor. To illustrate this idea, consider the production of ammonia by reaction of hydrogen and nitrogen:

[latex]\text{N}_2(g) + 3\text{H}_2(g) \longrightarrow 2\text{NH}_3(g)[/latex]

This equation shows ammonia molecules are produced from hydrogen molecules in a 2:3 ratio. Similar stoichiometric ratios may be derived using any amount (number) unit:

[latex]\frac{2 \;\text{NH}_3 \;\text{molecules}}{3 \;\text{H}_2 \;\text{molecules}} \;\text{or} \;\frac{2 \;\text{doz NH}_3 \;\text{molecules}}{3 \;\text{doz H}_2 \;\text{molecules}} \;\text{or} \;\frac{2 \;\text{mol NH}_3 \;\text{molecules}}{3 \;\text{mol H}_2 \;\text{molecules}}[/latex]

These stoichiometric ratios can be used to compute the number of ammonia molecules produced from a given number of hydrogen molecules, or the number of hydrogen molecules required to produce a given number of ammonia molecules. Similar factors may be derived for any pair of substances in any chemical equation.

Example 1

How many moles of I2 are required to react with 0.429 mol of Al according to the following equation (see Figure 1)?

[latex]2\text{Al} + 3\text{I}_2 \longrightarrow 2\text{AlI}_3[/latex]
This figure shows three photos with an arrow leading from one to the next. The first photo shows a small pile of iodine and aluminum on a white surface. The second photo shows a small amount of purple smoke coming from the pile. The third photo shows a large amount of purple and gray smoke coming from the pile.
Figure 1. Aluminum and iodine react to produce aluminum iodide. The heat of the reaction vaporizes some of the solid iodine as a purple vapor. (credit: modification of work by Mark Ott)

 

Solution

  • We are 0.429 mol of Al reacts, this is given. We are asked to determine a number of moles of I2.
  • Referring to the balanced chemical equation, the stoichiometric ratio relating the two substances of interest is [latex]\frac{3 \;\text{mol I}_2}{2 \;\text{mol Al}}[/latex]
  • The moles of I2 are expected to be greater than the moles of Al used, since 3 I2 are required for each 2 Al.

 

This figure shows two pink rectangles. The first is labeled, “Moles of A l.” This rectangle is followed by an arrow pointing right to a second rectangle labeled, “Moles of I subscript 2.”

[latex]\begin{array}{r @{{}={}} l} \text{mol I}_2 & 0.429 \;\rule[0.5ex]{3.25em}{0.1ex}\hspace{-3.25em}\text{mol Al} \times \frac{3 \;\text{mol I}_2}{2 \;\rule[0.25ex]{2em}{0.1ex}\hspace{-2em}\text{mol Al}} \\[1em] & 0.644 \;\text{mol I}_2 \end{array}[/latex]

 

Test Yourself
How many moles of Ca(OH)2 are required to react with 1.36 mol of H3PO4 to produce Ca3(PO4)2 according to the equation [latex]3\text{Ca(OH)}_2 + 2\text{H}_3 \text{PO}_4 \longrightarrow \text{Ca}_3 \text{(PO}_4)_2 + 6\text{H}_2 \text{O}[/latex] ?

 

Answer

2.04 mol

Example 2

How many carbon dioxide molecules are produced when 0.75 mol of propane is combusted according to this equation?

[latex]\text{C}_3 \text{H}_8 + 5\text{O}_2 \longrightarrow 3\text{CO}_2 + 4\text{H}_2 \text{O}[/latex]

 

Solution

  • 0.75 mol propane reacts. We are asked to determine a number of molecules of CO2 that forms.
  • Referring to the balanced chemical equation, the stoichiometric ratio relating the two substances of interest is [latex]\frac{3 \;\text{mol I}_2}{2 \;\text{mol Al}}[/latex] Stoichiometric ratios hold for moles of substances, or for molecules. In this case we have moles propane, so we can convert to moles of carbon dioxide. Once we have moles of carbon dioxide determined we will convert to molecules using Avogadro’s number (NA) in a second step.
  • The moles of carbon dioxide are expected to be greater than the moles of propane, since 3 of the product are made for each one propane reacted. After converting to moles this will be a very (very!) large number.

The balanced equation shows that carbon dioxide is produced from propane in a 3:1 ratio:

[latex]\frac{3 \;\text{mol CO}_2}{1 \;\text{mol C}_3 \text{H}_8}[/latex]

Using this stoichiometric factor, the provided molar amount of propane, and Avogadro’s number,

This figure shows two pink rectangles. The first is labeled, “Moles of C subscript 3 H subscript 8.” This rectangle is followed by an arrow pointing right to a second rectangle labeled, “Moles of C O subscript 2.”

[latex]0.75 \;\rule[0.5ex]{4.5em}{0.1ex}\hspace{-4.5em}\text{mol C}_3 \text{H}_8 \times \frac{3 \;\rule[0.25ex]{3em}{0.1ex}\hspace{-3em} \text{mol CO}_2}{1 \;\rule[0.5ex]{3em}{0.1ex}\hspace{-3em}\text{mol C}_3 \text{H}_8} \times \frac{6.022 \times 10^{23} \;\text{CO}_2 \;\text{molecules}}{\rule[0.25ex]{3em}{0.1ex}\hspace{-3em} \text{mol CO}_2} = 1.4 \times 10^{24} \text{CO}_2 \;\text{molecules}[/latex]

 

Test Yourself
How many NH3 molecules are produced by the reaction of 4.0 mol of Ca(OH)2 according to the following equation:

[latex](\text{NH}_4)_2 \text{SO}_4 + \text{Ca(OH)}_2 \longrightarrow 2\text{NH}_3 + \text{CaSO}_4 + 2\text{H}_2 \text{O}[/latex]
Answer
4.8 × 1024 NH3 molecules

These examples illustrate the ease with which the amounts of substances involved in a balanced chemical reaction may be related. But directly measuring numbers of atoms and molecules is not an easy task, and the practical application of stoichiometry requires that we use the more readily measured property of mass.

Example 3

What mass of sodium hydroxide, NaOH, would be required to produce 16 g of the antacid milk of magnesia [magnesium hydroxide, Mg(OH)2] by the following reaction?

[latex]\text{MgCl}_2(aq) + 2\text{NaOH}(aq) \longrightarrow \text{Mg(OH)}_2(s) + \text{NaCl}(aq)[/latex]

 

Solution
The approach used previously in Example 1 and Example 2 is likewise used here; that is, we must derive an appropriate stoichiometric factor from the balanced chemical equation and use it to relate the amounts of the two substances of interest. In this case, however, masses (not molar amounts) are provided and requested, so additional steps of the sort learned in the previous chapter are required. The calculations required are outlined in this flowchart:

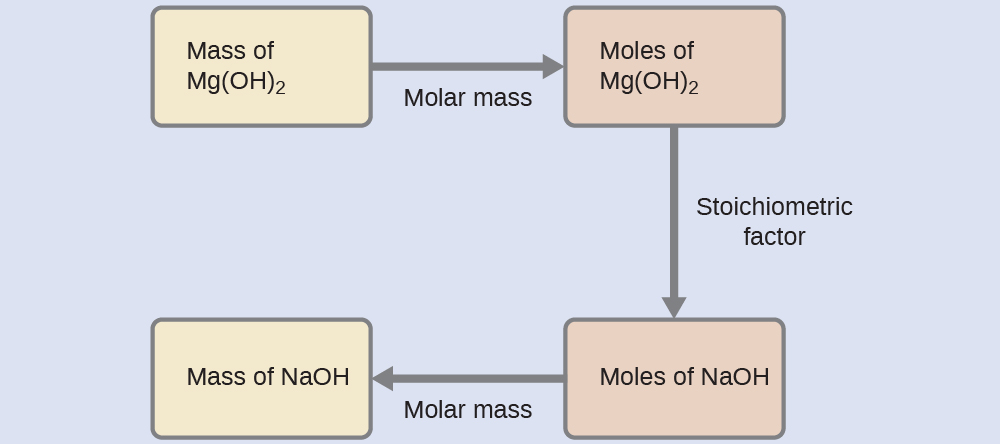
This figure shows four rectangles. The first is shaded yellow and is labeled, “Mass of M g ( O H ) subscript 2.” This rectangle is followed by an arrow pointing right to a second rectangle which is shaded pink and is labeled, “Moles of M g ( O H ) subscript 2.” This rectangle is followed by an arrow pointing right to a third rectangle which is shaded pink and is labeled, “Moles of N a O H.” This rectangle is followed by an arrow pointing right to a fourth rectangle which is shaded yellow and is labeled, “Mass of N a O H.”

[latex]16 \;\rule[0.5ex]{5em}{0.1ex}\hspace{-5em}\text{g Mg(OH)}_2 \times \frac{1 \;\rule[0.25ex]{4.75em}{0.1ex}\hspace{-4.75em}\text{mol Mg(OH)}_2}{58.3197 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{g Mg(OH)}_2} \times \frac{2 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol NaOH}}{1 \;\rule[0.25ex]{4.5em}{0.1ex}\hspace{-4.5em}\text{mol Mg(OH)}_2} \times \frac{39.9971 \;\text{g NaOH}}{1 \;\rule[0.25ex]{3.25em}{0.1ex}\hspace{-3.25em}\text{mol NaOH}} = 22 \;\text{g NaOH}[/latex]

 

Test Yourself
What mass of gallium oxide, Ga2O3, can be prepared from 29.0 g of gallium metal? The equation for the reaction is [latex]4 \text{Ga} + 3\text{O}_2 \longrightarrow 2\text{Ga}_2 \text{O}_3.[/latex]

 

Answer

39.0 g

Example 4

What mass of oxygen gas, O2, from the air is consumed in the combustion of 702 g of octane, C8H18, one of the principal components of gasoline?

[latex]2\text{C}_8 \text{H}_{18} + 25\text{O}_2 \longrightarrow 16\text{CO}_2 + 18\text{H}_2 \text{O}[/latex]

 

Solution
The approach required here is the same as for the Example 3, differing only in that the provided and requested masses are both for reactant species.

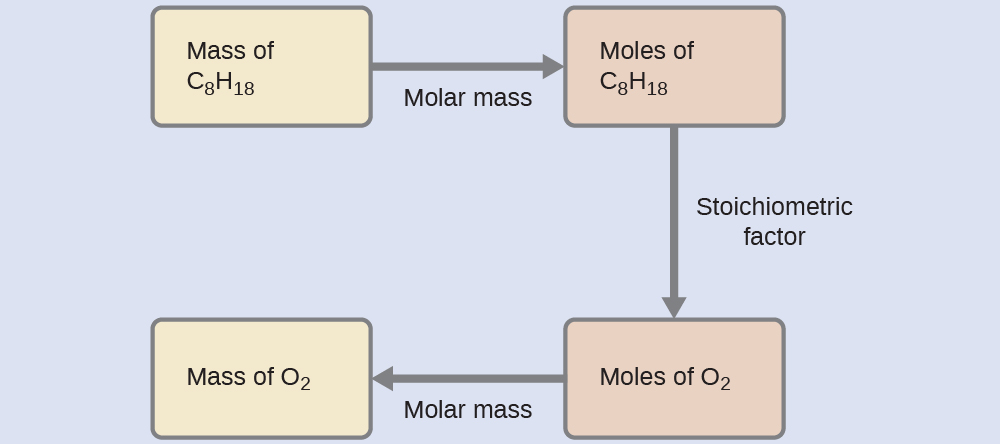
This figure shows four rectangles. The first is shaded yellow and is labeled, “Mass of C subscript 8 H subscript 18.” This rectangle is followed by an arrow pointing right to a second rectangle which is shaded pink and is labeled, “Moles of C subscript 8 H subscript 18.” This rectangle is followed by an arrow pointing right to a third rectangle which is shaded pink and is labeled, “Moles of O subscript 2.” This rectangle is followed by an arrow pointing right to a fourth rectangle which is shaded yellow and is labeled, “Mass of O subscript 2.”

[latex]702 \;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{g C}_8 \text{H}_{18} \times \frac{1 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol C}_8 \text{H}_{18}}{114.231 \;\rule[0.25ex]{2.75em}{0.1ex}\hspace{-2.75em}\text{g C}_8 \text{H}_{18}} \times \frac{25 \;\rule[0.25ex]{2.5em}{0.1ex}\hspace{-2.5em}\text{mol O}_2}{2 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol C}_8 \text{H}_{18}} \times \frac{31.9988 \;\text{g O}_2}{\rule[0.25ex]{2.5em}{0.1ex}\hspace{-2.5em}\text{mol O}_2} = 2.46 \times 10^3 \;\text{g O}_2[/latex]

 

Test Yourself
What mass of CO is required to react with 25.13 g of Fe2O3 according to the equation

[latex]\text{Fe}_2 \text{O}_3 + 3\text{CO} \longrightarrow 2\text{Fe} + 3\text{CO}_2[/latex]

 

Answer

13.2 g

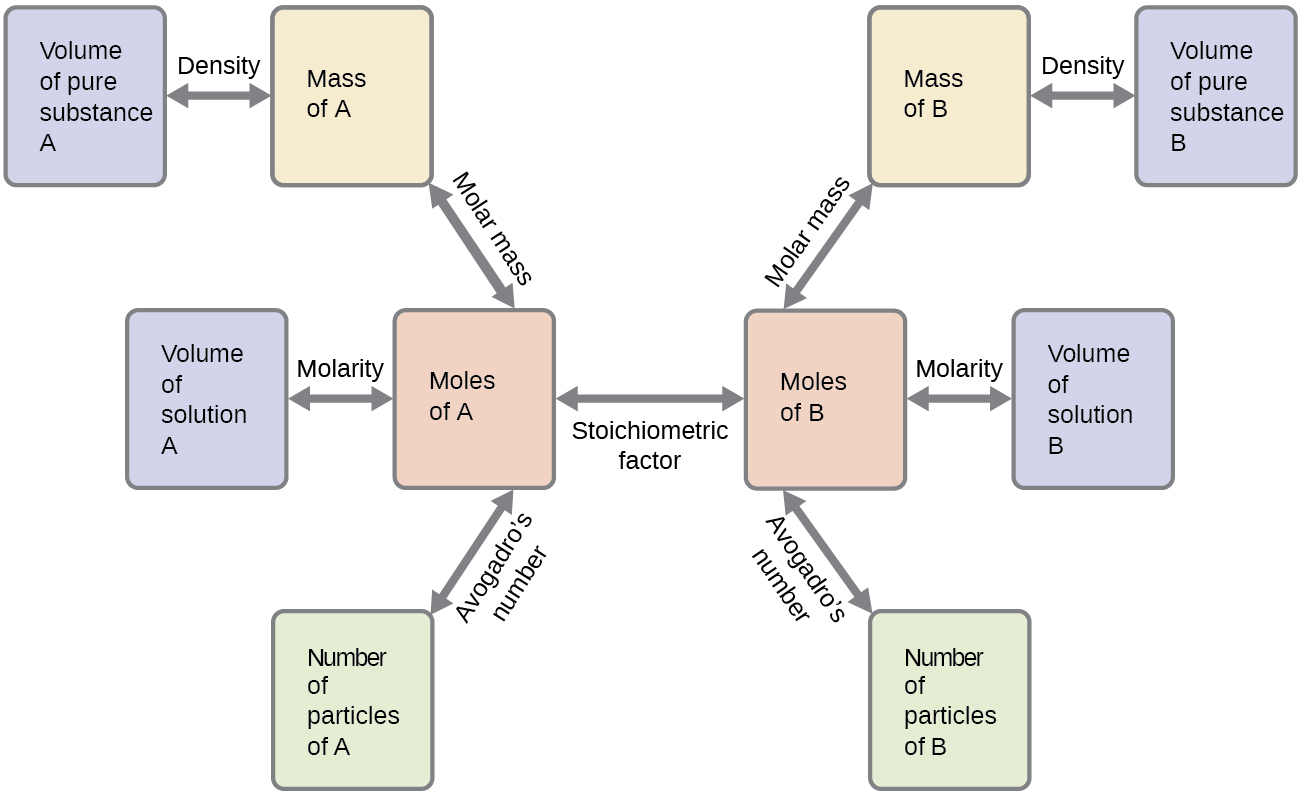
These examples illustrate just a few instances of reaction stoichiometry calculations. Numerous variations on the beginning and ending computational steps are possible depending upon what particular quantities are provided and sought (volumes, solution concentrations, and so forth). Regardless of the details, all these calculations share a common essential component: the use of stoichiometric factors derived from balanced chemical equations. Figure 2 provides a general outline of the various computational steps associated with many reaction stoichiometry calculations.

This flowchart shows 10 rectangles connected by double headed arrows. To the upper left, a rectangle is shaded lavender and is labeled, “Volume of pure substance A.” This rectangle is followed by a horizontal double headed arrow labeled, “Density.” It connects to a second rectangle which is shaded yellow and is labeled, “Mass of A.” This rectangle is followed by a double headed arrow which is labeled, “Molar Mass,” that connects to a third rectangle which is shaded pink and is labeled, “Moles of A.” To the left of this rectangle is a horizontal double headed arrow labeled, “Molarity,” which connects to a lavender rectangle which is labeled, “Volume of solution A.” The pink, “Moles of A,” rectangle is also connected with a double headed arrow below and to the left. This arrow is labeled “Avogadro’s number.” It connects to a green shaded rectangle that is labeled, “Number of particles of A.” To the right of the pink “Moles of A,” rectangle is a horizontal double headed arrow which is labeled, “Stoichiometric factor.” It connects to a second pink rectangle which is labeled, “Moles of B.” A double headed arrow which is labeled, “Molar mass,” extends from the top of this rectangle above and to the right to a yellow shaded rectangle labeled, “Mass of B.” A horizontal double headed arrow which is labeled, “Density” links to a lavender rectangle labeled, “Volume of substance B,” to the right. A horizontal double headed arrow labeled, “Molarity,” extends right to the of the pink “Moles of B” rectangle. This arrow connects to a lavender rectangle that is labeled, “Volume of substance B.” Another double headed arrow extends below and to the right of the pink “Moles of B” rectangle. This arrow is labeled “Avogadro’s number,” and it extends to a green rectangle which is labeled, “Number of particles of B.”
Figure 2. The flowchart depicts the various computational steps involved in most reaction stoichiometry calculations.

Airbags

Airbags (Figure 3) are a safety feature provided in most automobiles since the 1990s. The effective operation of an airbag requires that it be rapidly inflated with an appropriate amount (volume) of gas when the vehicle is involved in a collision. This requirement is satisfied in many automotive airbag systems through use of explosive chemical reactions, one common choice being the decomposition of sodium azide, NaN3. When sensors in the vehicle detect a collision, an electrical current is passed through a carefully measured amount of NaN3 to initiate its decomposition:

[latex] 2 \text{NaN}_3(s) \longrightarrow 3\text{N}_2(g) + 2\text{Na}(s)[/latex]
This photograph shows the inside of an automobile from the driver’s side area. The image shows inflated airbags positioned just in front of the driver’s and passenger’s seats and along the length of the passenger side over the windows. A large, round airbag covers the steering wheel.
Figure 3. Airbags deploy upon impact to minimize serious injuries to passengers. (credit: Jon Seidman)

 

This reaction is very rapid, generating gaseous nitrogen that can deploy and fully inflate a typical airbag in a fraction of a second (~0.03–0.1 s).

Among many engineering considerations, the amount of sodium azide used must be appropriate for generating enough nitrogen gas to fully inflate the air bag and ensure its proper function.

For example, a small mass (~100 g) of NaN3 will generate approximately 50 L of N2.

More Worked Out Problems

Example 5

How many molecules of SO3 are needed to react with 144 molecules of Fe2O3 given this balanced chemical equation?

Fe2O3(s) + 3SO3(g) [/latex]  \longrightarrow[/latex]  Fe2(SO4)3

 

Solution

We use the balanced chemical equation to construct a conversion factor between Fe2O3 and SO3. The number of molecules of Fe2O3 goes on the bottom of our conversion factor so it cancels with our given amount, and the molecules of SO3 go on the top. Thus, the appropriate conversion factor is

ss2

Starting with our given amount and applying the conversion factor, the result is

ss1

We need 432 molecules of SO3 to react with 144 molecules of Fe2O3.

 

Test Yourself

How many molecules of H2 are needed to react with 29 molecules of N2 to make ammonia if the balanced chemical equation is N2 + 3H2 [latex] \longrightarrow[/latex]  2NH3?

 

Answer

87 molecules

Example 6

How many molecules of NH3 can you make if you have 228 atoms of H2?

 

Solution

From the formula, we know that one molecule of NH3 has three H atoms. Use that fact as a conversion factor:

Screen-Shot-2014-07-17-at-10.49.40-AM

Test Yourself

How many molecules of Fe2(SO4)3 can you make from 777 atoms of S?

 

Answer

259 molecules

Example 7

How many moles of HCl will be produced when 249 g of AlCl3 are reacted according to this chemical equation?  The molar mass of AlCl3 is 133.34 g/mol.

2 AlCl3 + 3 H2O(ℓ) [latex] \longrightarrow[/latex]  Al2O3 + 6 HCl(g)

 

Solution

We will do this in two steps: convert the mass of AlCl3 to moles and then use the balanced chemical equation to find the number of moles of HCl formed. The molar mass of AlCl3 is 133.34 g/mol, which we have to invert to get the appropriate conversion factor:

[latex]249 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{g AlCl}_3 \times \frac{1 \;\text{mol AlCl}_3}{133.34\;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{g AlCl}_3} = \underline{1.86}74 \;\text{mol of aluminium chloride with 3 sig figs}[/latex]

 

Now we can use this quantity to determine the number of moles of HCl that will form. From the balanced chemical equation, we construct a conversion factor between the number of moles of AlCl3 and the number of moles of HCl:

[latex]\frac{6 \; \text{mol HCl}}{2 \; \text{mol AlCl}_3}[/latex]

Applying this conversion factor to the quantity of AlCl3, we get

[latex]\underline{1.86}74 \;\rule[0.5ex]{1.25em}{0.1ex}\hspace{-1.25em}\text{mol AlCl}_3 \times \frac{6 \;\text{mol HCl}}{2\;\rule[0.5ex]{1.25em}{0.1ex}\hspace{-1.25em}\text{mol AlCl}_3} =5.60 \;\text{mol HCl}[/latex]

Alternatively, we could have done this in one line:

[latex]249 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{g AlCl}_3 \times \frac{1 \;\rule[0.5ex]{1.25em}{0.1ex}\hspace{-1.25em}\text{mol AlCl}_3}{133.34\;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{g AlCl}_3} \times \frac{6 \;\text{mol HCl}}{2\;\rule[0.5ex]{1.25em}{0.1ex}\hspace{-1.25em}\text{mol AlCl}_3}=5.60 \;\text{mol HCl}[/latex]

The last digit in our final answer is slightly different because of rounding differences, but the answer is essentially the same.

 

Test Yourself

How many moles of Al2O3 will be produced when 23.9 g of H2O are reacted according to this chemical equation?

2 AlCl3 + 3 H2O(ℓ) [latex] \longrightarrow[/latex]  Al2O3 + 6 HCl(g)

 

Answer

0.442 mol

Key Concepts and Summary

A balanced chemical equation may be used to describe a reaction’s stoichiometry (the relationships between amounts of reactants and products). Coefficients from the equation are used to derive ratios that may be used for computations relating reactant and product masses, molar amounts, and other quantitative properties.

Review-Reflect, Extend

1. Think back to the pound cake recipe. What possible conversion factors can you construct relating the components of the recipe?

2. Determine the number of moles and the mass requested for each of the following reactions: (Hint: Write the balanced equation for each before attempting calculations.)

a) The number of moles and the mass of chlorine, Cl2, required to react with 10.0 g of sodium metal, Na, to produce sodium chloride, NaCl.

b) The number of moles and the mass of sodium nitrate, NaNO3, required to produce 128 g of oxygen. (NaNO2 is the other product.)

c) The number of moles and the mass of carbon dioxide formed by the combustion of 20.0 kg of carbon in an excess of oxygen.

3. Determine the number of moles and the mass requested for each of the following reactions: (Hint: Write the balanced equation for each before attempting calculations.)

a) The number of moles and the mass of water formed by the combustion of 20.0 kg of acetylene, C2H2, in an excess of oxygen.

b)
This figure includes two structural formulas. It reads, “The number of moles and the mass of,” which is followed by a structure with two C atoms connected with a horizontal double bond at the center. The C atom to the left has H atoms bonded above and to the left and below and to the left. The C atom to the right has H atoms bonded above and to the right and below and to the right. Following this structure, the figure reads, “required to react with H subscript 2 O to produce 9.55 g of,” which is followed by a structure with two C atoms connected with a horizontal single bond. The C atom to the left has H atoms bonded above, to the left, and below. The C atom to the right has H atoms bonded above and below. To the right, an O atom forms a single bond with the C atom. A single H atom is bonded to the right side of the O atom.

4. Silver is often extracted from ores such as K[Ag(CN)2] and then recovered by the reaction
[latex] 2 \text{K} [\text{Ag(CN)}_2](aq) + \text{Zn}(s) \longrightarrow 2\text{Ag}(s) + \text{Zn(CN)}_2(aq) + 2\text{KCN}(aq)[/latex]

a) How many molecules of Zn(CN)2 are produced by the reaction of 35.27 g of K[Ag(CN)2]?

b) What mass of Zn(CN)2 is produced?

5. What mass of CO2 is produced by the combustion of 1.00 mol of CH4?

CH4(g) + 2 O2(g) [latex]\longrightarrow[/latex] CO2(g) + 2 H2O(ℓ)

 

6. What mass of O2 can be generated by the decomposition of 100.0 g of NaClO3?

2 NaClO3 [latex]\longrightarrow[/latex] 2 NaCl(s) + 3 O2(g)

 Extend
  1. A car gets 27.5 miles per gallon on the highway. If gasoline contains 84.2% carbon by mass and has a density of 0.8205 g/mL, determine the mass of carbon dioxide produced during a 500-mile trip (3.785 liters per gallon).

Use factor-label so you can explain your answer.

 

Answers

 

2. a) 0.435 mol Na, 0.217 mol Cl2, 15.4 g Cl2

b) 8.00 mol NaNO3, 6.8 × 102 g NaNO3

c) 1665 mol CO2, 73.3 kg CO2

 

3.   a) 713 mol H2O, 12.8 kg H2O

b) 0.207 mol C2H4, 5.81 g C2H4

 

4.  [latex]\text{volume HCl solution} \longrightarrow \text{mol HCl} \longrightarrow \text{mol GaCl}_3[/latex]; b) 1.25 mol GaCl3, 2.2 × 102 g GaCl3

a) 5.337 × 1022 molecules      b) 10.41 g Zn(CN)2

5. 44.0 g

6. 45.1 g

 

 

Glossary

stoichiometric ratio: ratio of coefficients in a balanced chemical equation, used in computations relating amounts of reactants and products

stoichiometry: relationships between the amounts of reactants and products of a chemical reaction

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Chemistry Copyright © 2020 by Carol Higginbotham is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book