Wave/Particle Duality and the Uncertainty Principle

We’ve seen that electromagnetic radiation (a form of energy) can be viewed as a wave, or as a particle (a photon, or “packet”). That is, light has a dual nature. If energy can behave like a particle and a wave, can matter also exhibit this duality? It turns out that it does! In the 1920’s Louis Victor de Broglie showed that all moving particles can be described as wave-like. We call this general phenomenon wave/particle duality.

While it may seem odd to think of a physical object, such as a baseball, behaving like a wave, that is just what the theory suggests. However, for any object that is large, the particle nature is dominant and the wave nature is insignificant. But for tiny objects, such as electrons, the wave-like nature is physically meaningful and can be observed.

Around the same time, Werner Heisenberg proposed that the more accurately you know the position of a particle, the less you know about its momentum, and vice versa. This is now called the Heisenberg Uncertainty Principle. This means we can no longer talk about precise trajectories or locations of electrons. Instead, there is always some uncertainty and we can only talk about the PROBABILITY of finding an electron in a certain time and place.

The Schrödinger Wave Equation and the Wave Mechanics Model

Together, the quantization of energy, wave / particle duality and the Uncertainty Principle all led to Wave Mechanics, developed by Erwin Schrödinger in the 1920’s.

Schrödinger presented his Wave Mechanics in the form of a very complicated mathematical equation which, when solved gives us a series of WAVE FUNCTIONS, each having a specific energy.

A wave function is a mathematical function (like f(x) = x²), and we can plot a graph of the function (Figure 1) to get a picture of the ORBITAL—the space in which the electron is most likely to be found. Depending on the shape of the space, the orbitals have been assigned a name such as: s, p, d, and f. Note that an orbital is much different than an orbit!  An orbit is a set path on which an electron travels. We can’t talk about a set path because of the uncertaintly principle. An orbital is more like a probability map: the region in space where the electron is most likely to be over time.  The differing intensity of the shaded areas is an indication of electron density, which is a measure of the probability of locating an electron in a particular region of space (Figure 1 and 2).

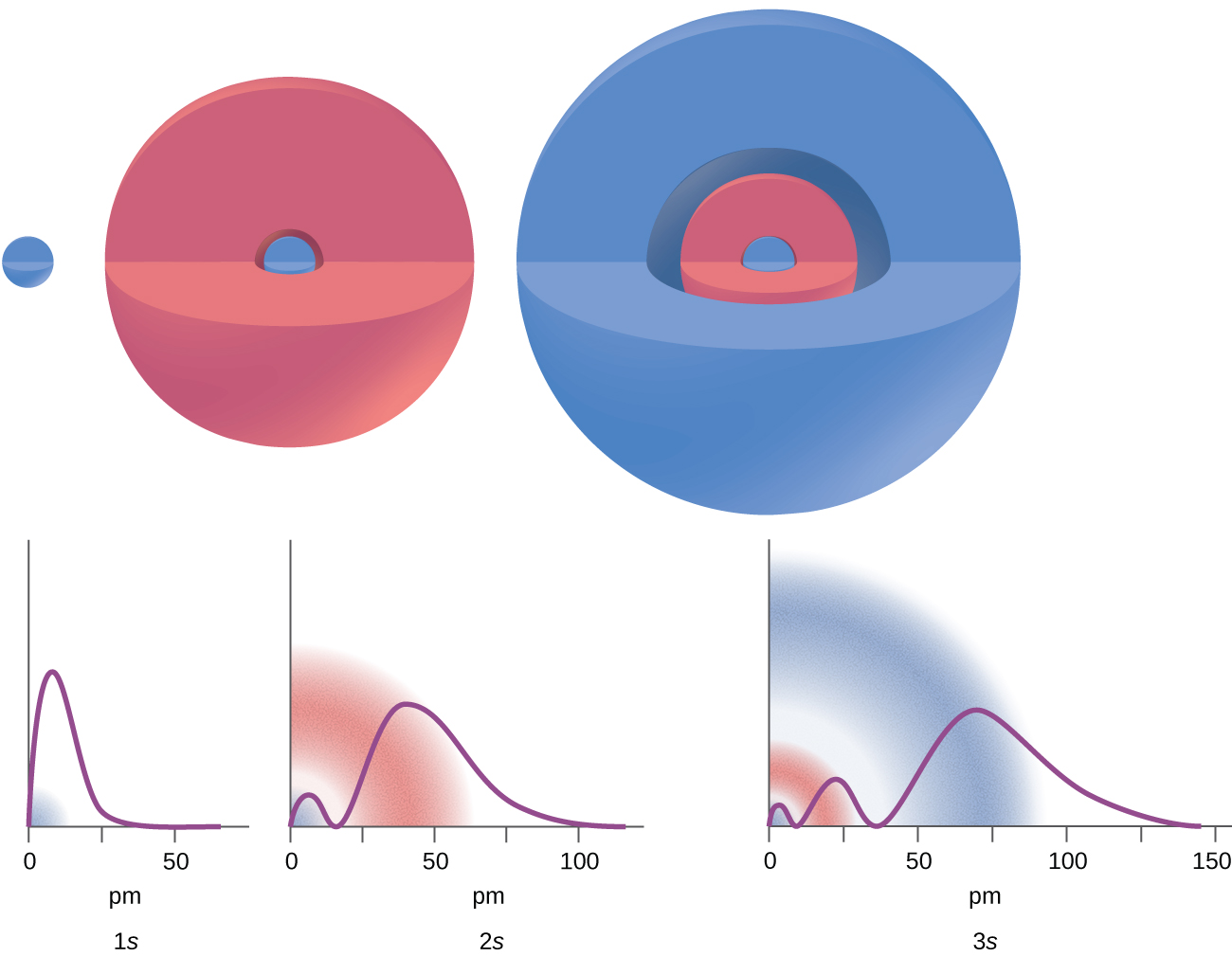
Looking at the probability maps of the electron in hydrogen (Figure 2), we can perhaps best picture an electron as a “cloud”. To simplify the picture of an orbital, however, we generally limit or define the orbital to be the zone within which the electron has 90% probability of being contained, and we represent this space with a solid. Figure 3 shows the many different complex shapes that the electron movement traces out. The s subshell electron density distribution is spherical and the p subshell has a dumbbell shape. The d and f orbitals are more complex. These shapes represent the three-dimensional regions within which the electron is likely to be found.  Keep in mind the “cloud” image when viewing these representations however.

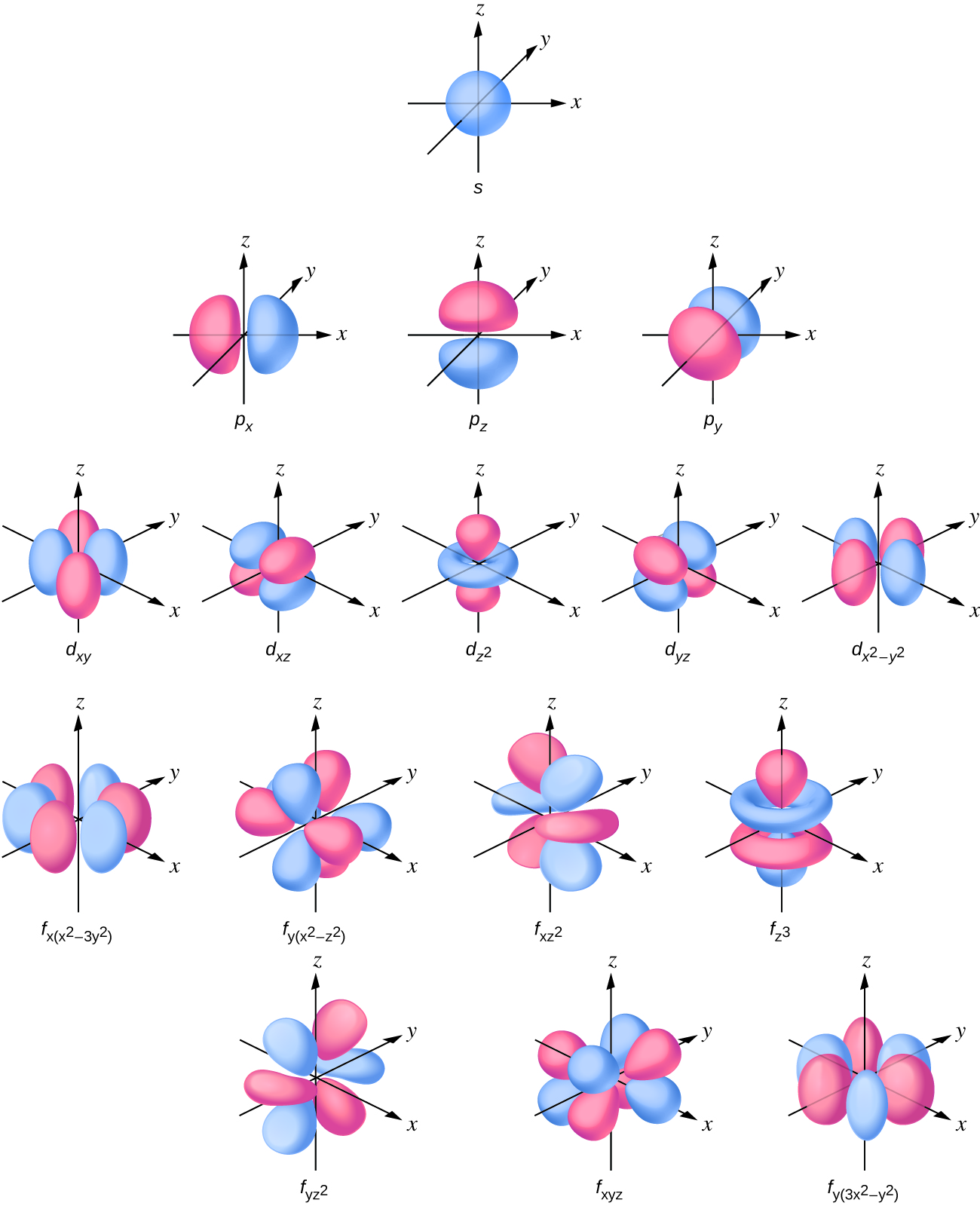
Describing atoms using the Wave Mechanics Model

Properties of electrons in orbitals

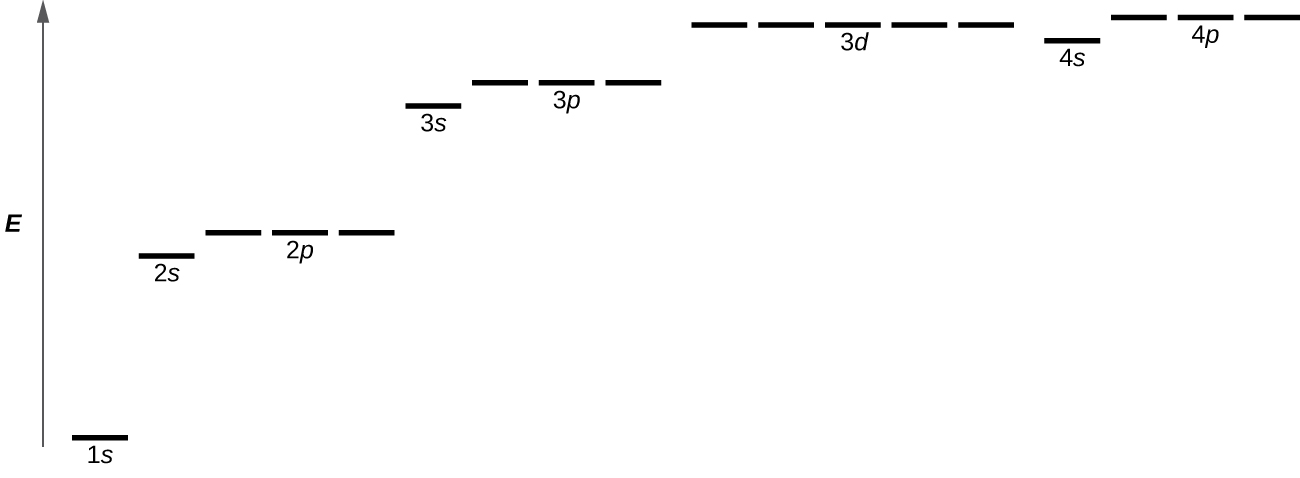
Orbitals are labeled with a number (known as the “shell”) followed by a letter (s, p, d, or f, known as the “subshell”), for example 1s, 2s, 2p, 3s. The subshells occur with a certain multiplicity; there are always seven f orbitals, five d orbitals, three p orbitals, and one s orbital (these could be called the “sub-subshells”). Any atom has all of these orbitals though they may or may not be occupied by electrons; those orbitals that are not occupied are available for possible excited states. Each orbital has a relative energy as shown in Figure 4, where the orbitals are represented as lines.

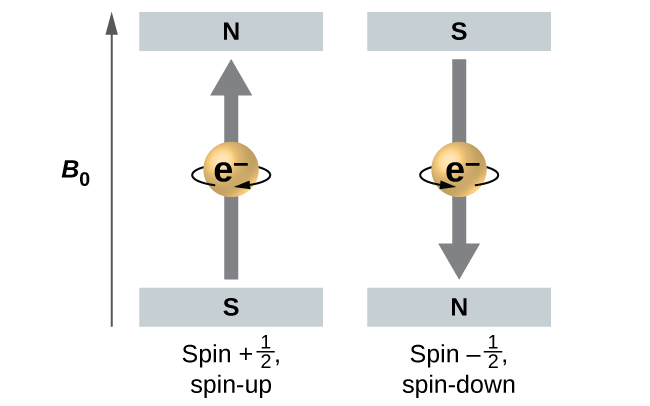
Electrons and other subatomic particles behave as if they are spinning (we cannot tell if they really are, but they behave as if they are). Electrons themselves have two possible spin states, spin up (graphically represented as an upward pointing arrow, ˦ ), and spin down (graphically represented as a downward pointing arrow, ˨ ). An orbital can hold a maximum of two electrons; when an orbital has two electrons in it, one electron will be spin up, and one will be spin down. This last aspect is an outcome of the Pauli Exclusion Principle, which states that no two electrons in the same atom can behave identically.