1 CHAPTER 1

An Introduction to Reason and Argument

This is an introductory textbook in logic and critical thinking that you are being asked to read as part of a course in Reason and Argument. Both logic and critical thinking centrally involve the analysis and assessment of arguments. While this may sound obtuse and disconnected from life, in reality, the skill set given to you by a course in logic and critical thinking will help you in many ways.

We live in a world filled with people who want to convince you to do something or to believe something. And you spend a great deal of your time sorting through these arguments. Should I buy a new car? Should I take out a student loan? Should I get a second job? Do I need to work out more? Will that toothpaste really make my teeth whiter?

A course in critical thinking (often called “reason and argument” in course catalogues) will provide you with practical steps you can use to make better decisions. You can think of this book and course as giving you defensive tools to protect yourself against false arguments. But this book and course will do more than this. They will also prepare you to better present your arguments. No matter your career, you will be asked to help persuade other people to follow your advice, to buy your product, or to make changes to their lives or to think thinking. Knowing how to create a reasonable argument will thus be a critical advantage to you and will enable you to be more successful in your career. Of course, the same is true for your personal life as well. Whether it is trying to convince your teenage son not to drink, or to help your significant other make an important career choice, or to engage successfully in a discussion with friends about issues that matter to you, the skills you learn by reading this book and taking this course will be of great help!

The “Thinker” by sculptor Auguste Rodin is often used to represent Philosophy and Logic (Source: Wikimedia)

Watch and Learn

Learn more about how to intellectually defend yourself with critical thinking skills by watching The Critical Thinker, Episode 2.

 

1.1 What Is An Argument?

“Argument” is a word that has multiple distinct meanings, so it is important to be clear from the start about the sense of the word that is relevant to the study of logic. In one sense of the word, an argument is a heated exchange of differing views as in the following:

Sally: Abortion is morally wrong and those who think otherwise are seeking to justify murder!

Bob: Abortion is not morally wrong and those who think so are right-wing bigots who are seeking to impose their narrow-minded views on all the rest of us!

Sally and Bob are having an argument in this exchange. That is, they are each expressing conflicting views in a heated manner. However, that is not the sense of “argument” with which logic is concerned.

Logic concerns a different sense of the word “argument.” An argument, in this sense, is a reason for thinking that a statement, claim or idea is true. For example:

Sally: Abortion is morally wrong because it is wrong to take the life of an innocent human being, and a fetus is an innocent human being.

In this example Sally has given an argument against the moral permissibility of abortion. That is, she has given us a reason for thinking that abortion is morally wrong. The conclusion of the argument is the first four words, “abortion is morally wrong.” But whereas in the first example Sally was simply asserting that abortion is wrong (and then trying to put down those who support it), in this example she is offering a reason for why abortion is wrong.

We can (and should) be more precise about our definition of an argument. But before we can do that, we need to introduce some further terminology that we will use in our definition. As I have already noted, the conclusion of Sally’s argument is that abortion is morally wrong. But the reason for thinking the conclusion is true is what we call the premise. So, we have two parts of an argument: the premise and the conclusion. Typically, a conclusion will be supported by two or more premises. Both premises and conclusions are statements. A statement is a type of sentence that can be true or false and corresponds to the grammatical category of a “declarative sentence.” For example, the sentence, “The Nile is a river in northeastern Africa,” is a statement. Why? Because it makes sense to inquire whether it is true or false. (In this case, it happens to be true.)

A sentence is still a statement even if it is false. For example, the sentence, “The Yangtze is a river in Japan,” is still a statement; it is just a false statement (the Yangtze River is in China). In contrast, the following sentences are NOT statements:

Please help yourself to more casserole.

Do not tell your mother about the surprise.

Do you like Vietnamese pho?

The reason that these sentences are not statements is that you cannot ask whether they are true or false (rather, they are requests or commands, and questions, respectively).

To summarize what we have learned so far:

All arguments are composed of premises and conclusions, which are both types of statements.

The premises of the argument provide a reason for thinking that the conclusion is true.

And arguments typically involve more than one premise.

A standard way of capturing the structure of an argument is by numbering the premises and conclusion. For example, recall Sally’s argument against abortion: “Abortion is morally wrong because it is wrong to take the life of an innocent human being, and a fetus is an innocent human being.”

To write the structure of Sally’s argument, we should create a numbered list of her main points:

It is morally wrong to take the life of an innocent human being

A fetus is an innocent human being

Therefore, abortion is morally wrong

Note that the last numbered statement (also denoted by the “therefore”) is the conclusion and the earlier numbered statements are the premises. This is what we call putting an argument into standard argument form.

We can now give a more precise definition of an argument.

“An argument is a set of statements, some of which (the premises) attempt to provide a reason for thinking that some other statement (the conclusion) is true.”

Although arguments are typically given in order to convince or persuade someone of the conclusion, the argument itself is independent of one’s attempt to use it to convince or persuade. For example, I have just given you this argument not in an attempt to convince you that abortion is morally wrong, but as an illustration of what an argument is. Later on in this chapter and in this book we will learn some techniques of evaluating arguments, but for now the goal is to learn to identify an argument, including its premises and conclusion(s). It is important to be able to identify arguments and understand their structure, whether or not you agree with conclusion of the argument. In the next section I will provide some techniques for being able to identify arguments.

1.2 Identifying Arguments

The best way to identify whether an argument is present is to ask whether there is a statement that someone is trying to establish as true by basing it on some other statement. If so, then there is an argument present. If not, then there is not. Another thing that can help in identifying arguments is knowing certain key words or phrases that are premise indicators or conclusion indicators. For example, recall Sally’s abortion argument:

Abortion is morally wrong because it is wrong to take the life of an innocent human being, and a fetus is an innocent human being.

The word “because” here is a premise indicator. That is, “because” indicates that what follows is a reason for thinking that abortion is morally wrong. Here is another example:

I know that the student plagiarized since I found the exact same sentences on a website and the website was published more than a year before the student wrote the paper.

In this example, the word “since” is a premise indicator because what follows it is a statement that is clearly intended to be a reason for thinking that the student plagiarized (i.e., a premise). Notice that in these two cases, the premise indicators “because” and “since” are interchangeable: I could have used “because” in place of “since” or “since” in the place of “because” and the meaning of the sentences would have been the same. In addition to premise indicators, there are also conclusion indicators. Conclusion indicators mark that what follows is the conclusion of an argument. For example,

Bob-the-arsonist has been dead for a year, so Bob-the-arsonist did not set the fire at the East Lansing Starbucks last week.

In this example, the word “so” is a conclusion indicator because what follows it is a statement that someone is trying to establish as true (i.e., a conclusion). Here is another example of a conclusion indicator:

A poll administered by Gallup (a respected polling company) showed candidate x to be substantially behind candidate y with only a week left before the vote, therefore candidate y will probably not win the election.

In this example, the word “therefore” is a conclusion indicator because what follows it is a statement that someone is trying to establish as true (i.e., a conclusion). As before, in both of these cases the conclusion indicators “so” and “therefore” are interchangeable: I could have used “so” in place of “therefore” or “therefore” in the place of “so” and the meaning of the sentences would have been the same.

The table below contains a list of some common premise and conclusion indicators:

Premise indicators	Conclusion indicators
since	therefore
because	so
for	hence
as	thus
given that	implies that
seeing that	consequently
for the reason that	it follows that
is shown by the fact that	we may conclude that

Although these words and phrases can be used to identify the premises and conclusions of arguments, they are not failsafe methods of doing so. Just because a sentence contains them does not mean that you are dealing with an argument. This can easily be shown by examples like these:

I have been running competitively since 1999.

I am so happy to have finally finished that class.

Although “since” can function as a premise indicator and although “so” can function as a conclusion indicator, neither one is doing so in these two examples. This shows that you cannot simply mindlessly use occurrences of these words in sentences to show that there is an argument being made. Rather, we have to rely on our understanding of the English sentence in order to determine whether an argument is being made or not.

Thus, the best way to determine whether an argument is present is by asking the question:

Is there a statement that someone is trying to establish as true or explain why it is true by basing it on some other statement?

If so, then there is an argument present. If not, then there is not. Notice that if we apply this method to the above examples, we will see that there is no argument present because there is no statement that someone is trying to establish as true by basing it on some other statement. For example, the sentence “I have been running competitively since 1999” just contains one statement, not two. But arguments always require at least two separate statements—one premise and one conclusion, so it cannot possibly be an argument.

Another way of explaining why these occurrences of “so” and “since” do not indicate that an argument is present is by noting that both premise indicators and conclusion indicators are, grammatically, conjunctions. A grammatical conjunction is a word that connects two separate statements. So, if a word or term is truly being used as a premise or conclusion indicator, it must connect two separate statements. Thus, if “since” were really functioning as a premise indicator in the above example then what followed it would be a statement. But “1999” is not a statement at all. Likewise, in the second example “so” is not being used as a conclusion indicator because it is not conjoining two separate statements. Rather, it is being used to modify the extent of “happy.” In contrast, if I were to say “Tom was sleeping, so he could not have answered the phone,” then “so” is being used as a conclusion indicator. In this case, there are clearly two separate statements (“Tom was sleeping” and “Tom could not have answered the phone”) and one is being used as the basis for thinking that the other is true.

If there is any doubt about whether a word is truly a premise/conclusion indicator or not, you can use the substitution test. Simply substitute another word or phrase from the list of premise indicators or conclusion indicators and see if the resulting sentence still makes sense. If it does, then you are probably dealing with an argument. If it does not, then you probably are not. For example, we can substitute “it follows that” for “so” in the Bob-the-arsonist example:

Bob-the-arsonist has been dead for a year, it follows that Bob-the-arsonist did not set the fire at the East Lansing Starbucks last week.

However, we cannot substitute “because” for “so” in the so-happy-I-finished-that-class example:

I am because happy to have finally finished that class.

Obviously, in the latter case the substitution of one conclusion indicator for another makes the sentence meaningless, which means that the “so” that occurred originally was not functioning as a conclusion indicator.

1.3 Arguments vs. Explanations

So far, I have defined arguments in terms of premises and conclusions, where the premises are supposed to provide a reason (support, evidence) for accepting the conclusion. Many times, the goal of giving an argument is simply to establish that the conclusion is true. For example, when I am trying to convince someone that obesity rates are rising in the U.S. I may cite evidence such as studies from the Center for Disease Control (CDC) and the National Institute of Health (NIH). The studies I cite would function as premises for the conclusion that obesity rates are rising. For example:

We know that obesity is on the rise in the U.S. because multiple studies carried out by the CDC and NIH have consistently shown a rise in obesity over the last four decades.

We could put this simple argument into standard form like this:

Multiple studies by the CDC and NIH have consistently shown a rise in obesity over the last four decades.

Therefore, obesity is on the rise in the U.S.

The standard form argument clearly distinguishes the premise from the conclusion and shows how the conclusion is supposed to be supported by the evidence offered in the premise. Again, the goal of this simple argument would be to convince someone that the conclusion is true. However, sometimes we already know that a statement or claim is true, and we are trying to establish why it is true rather than that it is true.

An argument that attempts to show why its conclusion is true is an explanation. Contrast the previous example with the following:

The reason that the rate of obesity is on the rise in the U.S. is that the foods we most often consume over the past four decades have increasingly contained high levels of sugar and low levels of dietary fiber. Since eating foods high in sugar and low in fiber triggers the insulin system to start storing those calories as fat, it follows that people who consume foods high in sugar and low in fiber will tend to store more of the calories consumed as fat.

This passage explains why obesity is on the rise in the U.S. Unlike the earlier example, here it is taken for granted that obesity is on the rise in the U.S. That is the claim whose truth we are trying to explain. We can put the obesity explanation into standard form just like any other argument. In order to do this, I will make some paraphrases of the premises and conclusion of the argument (for more on how to do this, see section 1.5 below).

Over the past four decades, Americans have increasingly consumed foods high in sugar and low in fiber.

Consuming foods high in sugar and low in fat triggers the insulin system to start storing those calories as fat.

When people store more calories as fat, they tend to become obese.

Therefore, the rate of obesity is on the rise in the U.S.

Notice that in this explanation the premises (1-3) attempt to give a reason for why the conclusion is true, rather than a reason for thinking that the conclusion is true. That is, in an explanation we assume that what we are trying to explain (i.e., the conclusion) is true. In this case, the premises are supposed to show why we should expect or predict that the conclusion is true. Explanations often give us an understanding of why the conclusion is true. We can think of explanations as a type of argument, we just have to distinguish two different types of argument: those that attempt to establish that their conclusion is true (arguments), and those that attempt to establish why their conclusion is true (explanations).

1.4 More Complex Argument Structures

So far, we have seen that an argument consists of a premise (typically more than one) and a conclusion. However, very often arguments and explanations have a more complex structure than just a few premises that directly support the conclusion. For example, consider the following argument:

No one living in Pompeii could have survived the eruption of Mt. Vesuvius. The reason is simple: the lava was flowing too fast and there was nowhere to go to escape it in time. Therefore, this account of the eruption, which claims to have been written by an eyewitness living in Pompeii, was not actually written by an eyewitness.

The main conclusion of this argument—the statement that depends on other statements as evidence but does not itself provide any evidence for any other statement—is:

A. This account of the eruption of Mt. Vesuvius was not actually written by an eyewitness.

However, the argument’s structure is more complex than simply having a couple of premises that provide evidence directly for the conclusion. Rather, some statement provides evidence directly for the main conclusion, but that statement itself is supported by another statement. To determine the structure of an argument, we must determine which statements support which.

We can use our premise and conclusion indicators to help with this. For example, the passage contains the phrase, “the reason is…” which is a premise indicator, and it also contains the conclusion indicator, “therefore.” That conclusion indicator helps us to identify the main conclusion, but the more important thing to see is that statement A does not itself provide evidence or support for any of the other statements in the argument, which is the clearest reason why statement A is the main conclusion of the argument. The next question we must answer is: which statement most directly supports A? What most directly supports

A is:

B. No one living in Pompeii could have survived the eruption of Mt. Vesuvius.

However, there is also a reason offered in support of B. That reason is that:

C. The lava from Mt. Vesuvius was flowing too fast and there was nowhere for someone living in Pompeii to go in order to escape it in time.

So, the main conclusion (A) is directly supported by B, and B is supported by C. Since B acts as a premise for the main conclusion but is also itself the conclusion of further premises, we refer to B as an intermediate conclusion. The important thing to recognize here is that one and the same statement can act as both a premise and a conclusion. Statement B is a premise that supports the main conclusion (A), but it is also itself a conclusion that follows from C. Here is how we would put this complex argument into standard form (using numbers this time, as we always do when putting an argument into standard form):

The lava from Mt. Vesuvius was flowing too fast and there was nowhere for someone living in Pompeii to go in order to escape it in time.

Therefore, no one living in Pompeii could have survived the eruption of Mt. Vesuvius. (from 1)

Therefore, this account of the eruption of Mt. Vesuvius was not actually written by an eyewitness. (from 2)

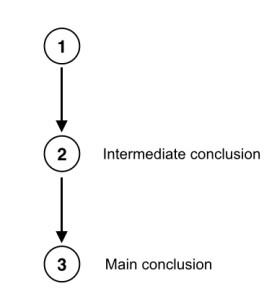Notice that at the end of statement 2 I have written in parentheses “from 1” (and likewise at the end of statement 3 I have written “from 2”). This is a shorthand way of saying: “this statement follows from statement 1.” We will use this convention as a way of keeping track of the structure of the argument.

The main argument here (from 2 to 3) contains a subargument, in this case the argument from 1 to 2. A subargument, as the term suggests, is a part of an argument that provides indirect support for the main argument. The main argument is the argument whose conclusion is the main conclusion.

It may also help to think about the structure of an argument spatially, as the figure to left demonstrates.

Another type of structure that arguments can have is when two or more premises provide direct but independent support for the conclusion. Here is an example of an argument with that structure:

I know that Wanda rode her bike to work today because when she arrived at work she had her right pant leg rolled up (which cyclists do in order to keep their pants legs from getting caught in the chain). Moreover, our coworker, Bob, who works in accounting, saw her riding towards work at 7:45 am.

The conclusion of this argument is “Wanda rode her bike to work today” and there are two premises that provide independent support for it: the fact that Wanda had her pant leg cuffed and the fact that Bob saw her riding her bike. Here is the argument in standard form:

Wanda arrived at work with her right pant leg rolled up.

Cyclists often roll up their right pant leg.

Bob saw Wanda riding her bike towards work at 7:45.

Therefore, Wanda rode her bike to work today. (from 1-2, 3 independently)

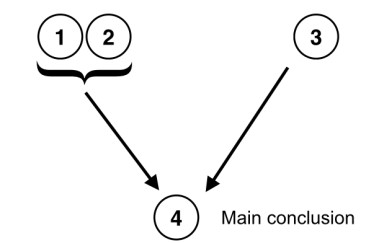Again, notice that next to statement 4 of the argument I have written the premises from which that conclusion follows. In this case, in order to avoid any ambiguity, I have noted that the support for the conclusion comes independently from statements 1 and 2, on the one hand, and from statement 3, on the other hand. It is important to point out that an argument or subargument can be supported by one or more premises. We see this in the present argument since the conclusion (4) is supported jointly by 1 and 2, and singly by 3. We can represent the structure of this argument spatially, as the figure to the right demonstrates.

There are endless different argument structures that can be generated from these few simple patterns. At this point, it is important to understand that arguments can have these different structures and that some arguments will be longer and more complex than others. Determining the structure of very complex arguments is a skill that takes some time to master. Even so, it may help to remember that any argument structure ultimately traces back to some combination of these.

1.5 Using Your Own Paraphrases Of Premises And Conclusions To Reconstruct Arguments In Standard Form

Although sometimes we can just lift the premises and conclusion verbatim from the argument, we cannot always do this. Paraphrases of premises or conclusions are sometimes needed in order to make the standard form argument as clear as possible. A paraphrase is the use of different words to capture the same idea in a clearer way. There will always be multiple ways of paraphrasing premises and conclusions and this means that there will never be just one way of putting an argument into standard form. In order to paraphrase well, you will have to rely on your understanding of English to come up with what you think is the best way of capturing the essence of the argument. Again, typically there is no single right way to do this, although there are certainly better and worse ways of doing it. For example, consider the following argument:

Just because Jeremy’s prints were on the gun that killed Tim and the gun was registered to Jeremy, it does not follow that Jeremy killed Tim since Jeremy’s prints would certainly be on his own gun and someone else could have stolen Jeremy’s gun and used it to kill Tim.

What is the conclusion of this argument? (Think about it before reading on.) Here is one way of paraphrasing the conclusion:

The fact that Jeremy’s prints were on the gun that killed Tim and the gun was registered to Jeremy does not mean that Jeremy killed Tim.

This statement seems to capture the essence of the main conclusion in the above argument. The premises of the argument would be:

Jeremy’s prints would be expected to be on a gun that was registered to him

Someone could have stolen Jeremy’s gun and then used it to kill Tim

Notice that while I have paraphrased the first premise, I have left the second premise almost exactly as it appeared in the original paragraph. As I have said, paraphrases are needed in order to try to make the standard form argument as clear as possible and this is what I have tried to do in capturing premise 1 as well as the conclusion of this argument. So here is the reconstructed argument in standard form:

Jeremy’s prints would be expected to be on a gun that was registered to him

Someone could have stolen Jeremy’s gun and then used it to kill Tim

Therefore, the fact that Jeremy’s prints were on the gun that killed Tim and the gun was registered to Jeremy does not mean that Jeremy killed Tim. (from 1-2)

However, as I have just noted, there is more than one way of paraphrasing the premises and conclusion of the argument. To illustrate this, I will give a second way that one could accurately capture this argument in standard form. Here is another way of expressing the conclusion:

We do not know that Jeremy killed Tim.

That is clearly what the above argument is trying to ultimately establish and it is a much simpler (in some ways) conclusion than my first way of paraphrasing the conclusion. However, it also takes more liberties in interpreting the argument than my original paraphrase. For example, in the original argument there is no occurrence of the word “know.” That is something that I am introducing in my own paraphrase. That is a totally legitimate thing to do, as long as introducing new terminology helps us to clearly express the essence of the premise or conclusion that we are trying to paraphrase. Since my second paraphrase of the conclusion differs from my first paraphrase, you can expect that my premises will differ also. So how shall I paraphrase the premises that support this conclusion? Here is another way of paraphrasing the premises and putting the argument into standard form:

Tim was killed by a gun that was registered to Jeremy and had Jeremy’s prints on it.

It is possible that Jeremy’s gun was stolen from him.

If Jeremy’s gun was stolen from him, then Jeremy could not have killed Tim.

Therefore, we do not know that Jeremy killed Tim. (from 1-3)

Notice that this standard form argument has more premises than my first reconstruction of the standard form argument (which consisted of only three statements). I have taken quite a few liberties in interpreting and paraphrasing this argument, but what I have tried to do is to get down to the most essential logic of the original argument. The paraphrases of the premises I have used are quite different from the wording that occurs in the original paragraph. I have introduced phrases such as “it is possible that” as well as conditional statements (if…then statements), such as premise 3. Nonetheless, this reconstruction seems to get at the essence of the logic of the original argument. As long as your paraphrases help you to do that, they are good paraphrases. Being able to reconstruct arguments like this takes many years of practice in order to do it well, and much of the material that we will learn later in the text will help you to better understand how to capture an argument in standard form, but for now it is important to recognize that there is never only one way of correctly capturing the standard form of an argument. And the reason for this is that there are multiple, equally good, ways of paraphrasing the premises and conclusion of an argument.

1.6. Validity

Watch and Learn

Learn about Validity in Arguments by watching the Wireless Philosophy video: Fundamentals: Validity

So far we have discussed what arguments are and how to determine their structure, including how to reconstruct arguments in standard form. But we have not yet discussed what makes an argument good or bad. The central concept that you will learn in logic is the concept of validity. Validity relates to how well the premises support the conclusion, and it is the golden standard that every argument should aim for. A valid argument is an argument whose conclusion cannot possibly be false, assuming that the premises are true. Another way of putting this is as a conditional statement: A valid argument is an argument in which if the premises are true, the conclusion must be true. Here is an example of a valid argument:

Violet is a dog

Therefore, Violet is a mammal (from 1)

You might wonder whether it is true that Violet is a dog (maybe She is a lizard or a buffalo—we have no way of knowing from the information given). But, for the purposes of validity, it does not matter whether premise 1 is actually true or false. All that matters for validity is whether the conclusion follows from the premise. And we can see that the conclusion, Violet is a mammal, does seem to follow from the premise, Violet is a dog. That is, given the truth of the premise, the conclusion has to be true. This argument is clearly valid since if we assume that “Violet is a dog” is true, then, since all dogs are mammals, it follows that “Violet is a mammal” must also be true. As we have just seen, whether or not an argument is valid has nothing to do with whether the premises of the argument are actually true or not. We can illustrate this with another example, where the premises are clearly false:

Everyone born in France can speak French

Barack Obama was born in France

Therefore, Barak Obama can speak French (from 1-2)

This is a valid argument. Why? Because when we assume the truth of the premises (everyone born in France can speak French, Barack Obama was born in France) the conclusion (Barack Obama can speak French) must be true. Notice that this is so even though none of these statements is actually true. Not everyone born in France can speak French (think about people who were born there but then moved somewhere else where they did not speak French and never learned it) and Obama was not born in France, but it is also false that Obama can speak French. So we have a valid argument even though neither the premises nor the conclusion is actually true. That may sound strange, but if you understand the concept of validity, it is not strange at all. Remember: validity describes the relationship between the premises and conclusion, and it means that the premises imply the conclusion, whether or not that conclusion is true. In order to better understand the concept of validity, Let uslook at an example of an invalid argument:

George was President of the United States

Therefore, George was elected President of the United States (from 1)

This argument is invalid because it is possible for the premise to be true and yet the conclusion false. Here is a counterexample to the argument. Gerald Ford was President of the United States but he was never elected president, since Ford Replaced Richard Nixon when Nixon resigned in the wake of the Watergate scandal. So it does not follow that just because someone is President of the United States that they were elected President of the United States. In other words, it is possible for the premise of the argument to be true and yet the conclusion false. And this means that the argument is invalid. If an argument is invalid it will always be possible to construct a counterexample to show that it is invalid (as I have done with the Gerald Ford scenario). A counterexample is simply a description of a scenario in which the premises of the argument are all true while the conclusion of the argument is false.

In order to determine whether an argument is valid or invalid we can use what I’ll call the informal test of validity. To apply the informal test of validity ask yourself whether you can imagine a world in which all the premises are true and yet the conclusion is false. If you can imagine such a world, then the argument is invalid. If you cannot imagine such a world, then the argument is valid. Notice: it is possible to imagine a world where the premises are true even if the premises are not, as a matter of actual fact, true. This is why it does not matter for validity whether the premises (or conclusion) of the argument are actually true. It will help to better understand the concept of validity by applying the informal test of validity to some sample arguments.

Joan jumped out of an airplane without a parachute

Therefore, Joan fell to her death (from 1)

To apply the informal test of validity we have to ask whether it is possible to imagine a scenario in which the premise is true and yet the conclusion is false (if so, the argument is invalid). So, can we imagine a world in which someone jumped out of an airplane without a parachute and yet did not fall to her death? (Think about it carefully before reading on.) As we will see, applying the informal test of validity takes some creativity, but it seems clearly possible that Joan could jump out of an airplane without a parachute and not die—she could be perfectly fine, in fact. All we have to imagine is that the airplane was not operating and in fact was on the ground when Joan jumped out of it. If that were the case, it would be a) true that Joan jumped out of an airplane without a parachute and yet b) false that Joan fell to her death. Thus, since it is possible to imagine a scenario in which the premise is true and yet the conclusion is false, the argument is invalid. Let us slightly change the argument, this time making it clear that the plane is flying:

• Joan jumped out of an airplane travelling 300 mph at a height of 10,000 ft without a parachute
• Joan fell to her death (from 1)

Is this argument valid? You might think so since you might think that anyone who did such a thing would surely die. But is it possible to not die in the scenario described by the premise? If you think about it, you’ll realize that there are lots of ways someone could survive. For example, maybe someone else who was wearing a parachute jumped out of the plane after them, caught them and attached the parachute-less person to them, and then pulled the ripcord and they both landed on the ground safe and sound. Or maybe Joan was performing a stunt and landed in a giant net that had been set up for that purpose. Or maybe she was just one of those people who, although they did fall to the ground, happened to survive (it has happened before). All of these scenarios are consistent with the information in the first premise being true and also consistent with the conclusion being false. Thus, again, any of these counterexamples show that this argument is invalid. Notice that it is also possible that the scenario described in the premises ends with Joan falling to her death. But that does not matter because all we want to know is whether it is possible that she does not. And if it is possible, what we have shown is that the conclusion does not logically follow from the premise alone. That is, the conclusion does not have to be true, even if we grant that the premise is. And that means that the argument is not valid (i.e., it is invalid).

Let us switch examples and consider a different argument.

A person can be President of the United States only if they were born in the United States.

Obama is President of the United States.

Kenya is not in the United States.

Therefore, Obama was not born in Kenya (from 1-3)

In order to apply the informal test of validity, we have to ask whether we can imagine a scenario in which the premises are both true and yet the conclusion is false. So, we have to imagine a scenario in which premises 1, 2, and 3 are true and yet the conclusion (“Obama was not born in Kenya”) is false. Can you imagine such a scenario? You cannot. The reason is that if you are imagining that it is a) true that a person can be President of the United States only if they were born in the United States, b) true that Obama is president and c) true that Kenya is not in the U.S., then it must be true that Obama was not born in Kenya. Thus we know that on the assumption of the truth of the premises, the conclusion must be true. And that means the argument is valid. In this example, however, premises 1, 2, and 3 are not only assumed to be true but are actually true. However, as we have already seen, the validity of an argument does not depend on its premises actually being true. Here is another example of a valid argument to illustrate that point.

A person can be President of the United States only if they were born in Kenya

Obama is President of the United States

Therefore, Obama was born in Kenya (from 1-2)

Clearly, the first premise of this argument is false. But if we were to imagine a scenario in which it is true and in which premise 2 is also true, then the conclusion (“Obama was born in Kenya”) must be true. And this means that the argument is valid. We cannot imagine a scenario in which the premises of the argument are true and yet the conclusion is false. The important point to recognize here—a point I have been trying to reiterate throughout this section—is that the validity of the argument does not depend on whether or not the premises (or conclusion) are actually true. Rather, validity depends only on the logical relationship between the premises and the conclusion. The actual truth of the premises is, of course, important to the quality of the argument, since if the premises of the argument are false, then the argument does not provide any reason for accepting the conclusion. In the next section we will address this topic.

1.7 Soundness

Watch and Learn

Learn more about Soundness by watching the Wireless Philosophy video: Fundamentals: Soundness.

A good argument is not only valid, but also sound. Soundness is defined in terms of validity, so since we have already defined validity, we can now rely on it to define soundness. A sound argument is a valid argument that has all true premises. That means that the conclusion of a sound argument will always be true. Why? Because if an argument is valid, the premises transmit truth to the conclusion on the assumption of the truth of the premises. But if the premises are actually true, as they are in a sound argument, then since all sound arguments are valid, we know that the conclusion of a sound argument is true. Compare the last two Obama examples from the previous section. While the first argument was sound, the second argument was not sound, although it was valid. The relationship between soundness and validity is easy to specify: all sound arguments are valid arguments, but not all valid arguments are sound arguments.

Although soundness is what any argument should aim for, we will not be talking much about soundness in this book. The reason for this is that the only difference between a valid argument and a sound argument is that a sound argument has all true premises. But how do we determine whether the premises of an argument are actually true? Well, there are lots of ways to do that, including using Google to look up an answer, studying the relevant subjects in school, consulting experts on the relevant topics, and so on. But none of these activities have anything to do with logic, per se. The relevant disciplines to consult if you want to know whether a particular statement is true is almost never logic! For example, logic has nothing to say regarding whether or not protozoa are animals or whether there are predators that are not in the animal kingdom. In order to learn whether those statements are true, we would have to consult biology, not logic. Since this is a logic textbook, however, it is best to leave the question of what is empirically true or false to the relevant disciplines that study those topics. And that is why the issue of soundness, while crucial for any good argument, is outside the purview of logic.

1.8 Deductive vs. Inductive Arguments

Watch and Learn

Learn about Deductive Arguments by watching the Wireless Philosophy video: Fundamentals: Deductive Arguments.

The concepts of validity and soundness that we have introduced apply only to the class of what are called “deductive arguments”. A deductive argument is an argument whose conclusion is supposed to follow from its premises with absolute certainty, thus leaving no possibility that the conclusion does not follow from the premises. For a deductive argument to fail to do this is for it to fail as a deductive argument. In contrast, an inductive argument is an argument whose conclusion is supposed to follow from its premises with a high level of probability, which means that although it is possible that the conclusion does not follow from its premises, it is unlikely that this is the case. Here is an example of an inductive argument:

Tweets is a healthy, normally functioning bird and since most healthy, normally functioning birds fly, Tweets probably flies.

Notice that the conclusion, Tweets probably flies, contains the word “probably.” This is a clear indicator that the argument is supposed to be inductive, not deductive. Here is the argument in standard form:

Tweets is a healthy, normally functioning bird

Most healthy, normally functioning birds fly

Therefore, Tweets probably flies

Given the information provided by the premises, the conclusion does seem to be well supported. That is, the premises do give us a strong reason for accepting the conclusion. This is true even though we can imagine a scenario in which the premises are true and yet the conclusion is false. For example, suppose that we added the following premise:

Tweets is 6 ft tall and can run 30 mph.

Were we to add that premise, the conclusion would no longer be supported by the premises, since any bird that is 6 ft tall and can run 30 mph, is not a kind of bird that can fly. That information leads us to believe that Tweets is an ostrich or emu, which are not kinds of birds that can fly. As this example shows, inductive arguments are defeasible arguments since by adding further information or premises to the argument, we can overturn (defeat) the verdict that the conclusion is well-supported by the premises. Inductive arguments whose premises give us a strong, even if defeasible, reason for accepting the conclusion are called, unsurprisingly, strong inductive arguments. In contrast, an inductive argument that does not provide a strong reason for accepting the conclusion are called weak inductive arguments.

Whereas strong inductive arguments are defeasible, valid deductive arguments are not. Suppose that instead of saying that most birds fly, premise 2 said that all birds fly.

Tweets is a healthy, normally function bird.

All healthy, normally functioning birds can fly.

Therefore, Tweets can fly.

This is a valid argument and since it is a valid argument, there are no further premises that we could add that could overturn the argument’s validity. (True, premise 2 is false, but as we have seen that is irrelevant to determining whether an argument is valid.) Even if we were to add the premise that Tweets is 6 ft tall and can run 30 mph, it does not overturn the validity of the argument. As soon as we use the universal generalization, “all healthy, normally function birds can fly,” then when we assume that premise is true and add that Tweets is a healthy, normally functioning bird, it has to follow from those premises that Tweets can fly. This is true even if we add that Tweets is 6 ft tall because then what we have to imagine (in applying our informal test of validity) is a world in which all birds, including those that are 6 ft tall and can run 30 mph, can fly.

Although inductive arguments are an important class of argument that are commonly used every day in many contexts, logic texts tend not to spend as much time with them since we have no agreed upon standard of evaluating them. In contrast, there is an agreed upon standard of evaluation of deductive arguments. We have already seen what that is; it is the concept of validity. There are no such agreed upon formal methods of evaluation for inductive arguments.

Chapter Review

Review what you have learned about the fundamentals of Philosophical Reasoning by watching Crash Course in Philosophy #2. This video covers the material presented in this chapter.