3 CHAPTER 3
Categorical Logic
Categorical logic is the logic that deals with the logical relationship between categorical statements. A categorical statement is simply a statement about a category or type of thing. For example, the first premise of the above argument is a statement about the categories of humans and things that are mortal.
The second premise is a statement about the categories of things that are mortal and things that die. Finally, the conclusion is a statement about humans and things that die.
|
Watch and Learn |
|
Learn about Categorical Statements by watching A Crash Course in Formal Logic Pt 5a: Categorical Statements. |
In categorical logic, the logical terms are the terms “all” and “some.” We will use capital letters to stand for categories of things in the world. Thus, we can represent the statement:
All humans are mortal as All H are M
where “H” stands for the category of “humans” and “M” stands for the category, “things that are mortal.” Notice that the categories are nouns or noun phrases. Thus, instead of saying that the category is “mortal” I said the category is “things that are mortal.” In categorical logic, the capital letters stand for noun phrases that denote categories of things in the world—for example, “cars” or “things that are man-made” or “mammals” or “things that are red.”
3.1. Venn Diagrams
|
Watch and Learn |
|
Learn about Venn Diagrams by watching A Crash Course in Formal Logic Pt 6b: Venn Diagrams. |
One way to evaluate Categorical Statements is to use Venn diagrams to represent the logical relationships between the different kinds of categorical statements. A Venn diagram is simply a way of graphically representing the logical relationship between two different categorical statements.
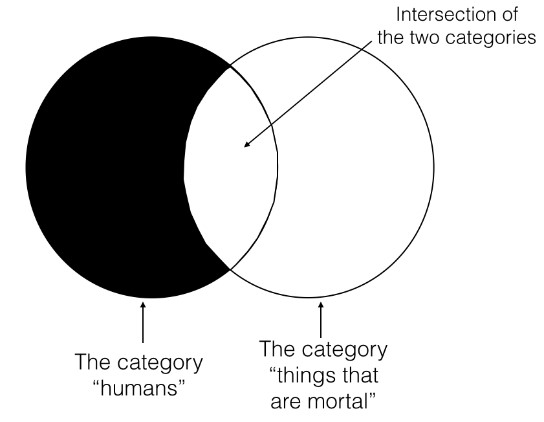
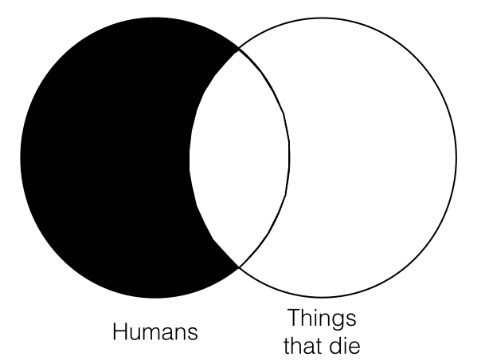
Here is how to understand this Venn. There are two circles that represent the two categories, “humans” and “things that are mortal.” These two categories are overlapping so that the intersection of those two categories (i.e., the place where the two circles overlap) represents things that are both human and mortal. Any shaded portions of the Venn diagram (by “shaded” I will mean “blacked out”) represent that there is nothing in that area of the category. So, the above Venn says that there is nothing in the category “humans” that is not also in the category “things that are mortal.” The above Venn also allows that there are things that are in the category “things that are mortal” but that are not in the category “humans” (which is as it should be since, of course, dogs are mortal and yet not human). So, the reason the category “things that are mortal” is left unshaded is that in saying “all humans are mortal” I leave open the possibility that there are things that are not human and yet mortal.
As noted above, the statement, “all humans are mortal,” has a particular form:
All H are M.
This is one of the four categorical forms. The way we will represent these categorical forms generally are with an “S” (which stands for “subject term”) and a “P” (which stands for “predicate term”). Thus, the categorical statement, “all humans are mortal,” has the following categorical form:
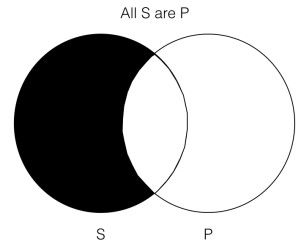
All S are P.
The way we interpret statements of this form are as follows: everything in the category S is also in the category P. This statement form is what we call a “universal affirmative,” since it is a universal statement that does not contain a negation. There are three other categorical statement forms that you will have to become familiar with in order to do categorical logic. Here they are (with the name of the type of statement in parentheses to the right:
No S are P (universal negative)
Some S are P (particular affirmative)
Some S are not P (particular negative)
Here are three examples of statements that have these three forms (respectively):
No reptiles give live birth (universal negative)
Some birds are taller than President
Obama (particular affirmative)
Some birds do not fly (particular negative)
Notice that although these three statements do not have exactly the same form as the statement forms above, they can be translated into those same forms. All we have to do is figure out the noun phrase that describes each category that the statement is referring to. Let usstart with “no reptiles give live birth.” This categorical statement refers to two different categories: the category of “reptiles” and the category of “things that give live birth.” Notice, again, that I added “things that…” to the predicate of the sentence (“give live birth”) because “give live birth” is not a description of a category. Rather, the way of describing the category is with the noun phrase, “things that give live birth.” Using these two category descriptions, we can translate this sentence to have the same form as its categorical form. All we have to do is substitute in the name of the subject category (i.e., the “S” term) and the description of the predicate category (i.e., the “P” term). Doing that will yield the following sentence:
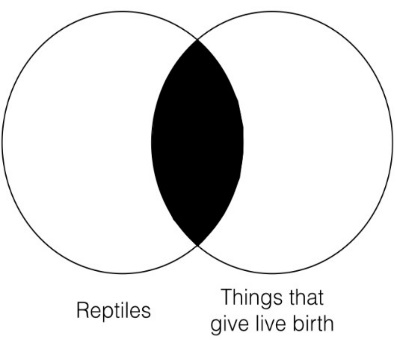
No reptiles are things that give live birth
Although this sentence sounds strange in English, it has the same form as the categorical form, no S are P, and this translation allows us to clearly see that it does and thus to see what the two categories are. To the left is what the Venn diagram for this statement looks like.
This Venn diagram represents that there is nothing in the intersection of the two categories, “reptiles” and “things that give live birth.” If you think about it, this is exactly what our original statement was saying: there is not anything that is both a reptile and gives live birth.
Let us look at the next statement, “some birds are taller than President Obama.” This is a statement not about all birds, but about some birds. What are the two categories? One category is clearly “birds.” The other category is “things that are taller than President Obama.” That may sound like a
strange category, but it is perfectly legitimate category. It includes things like adult ostriches, large grizzly bears standing on their hind legs, giraffes, the Flatiron Building, a school bus, etc. Here is how we would translate this sentence using our two categories:
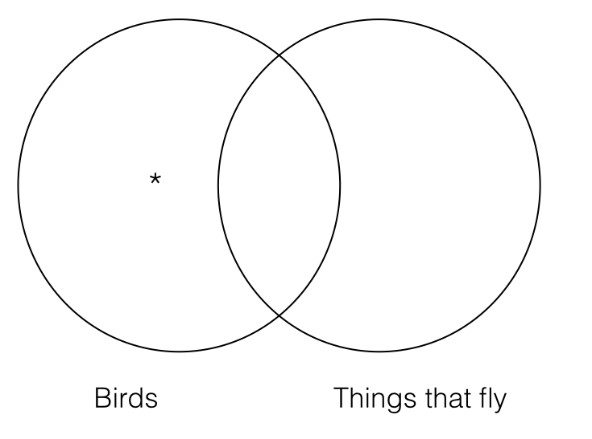
Some birds are things that are taller than President Obama.
Again, although this sentence sounds strange in English, it has the same form as the categorical form, some S are P, and it allows us to clearly see what the two categories are. To the left is the Venn diagram for this statement.
By convention, an asterisk on the Venn diagram means that there is at least one thing in that category. By putting the asterisk in the intersection of the two categories, we are saying that there is at least one thing that is a bird and is taller than President Obama, which is exactly what our original sentence was saying.

Finally, let us consider the statement, “some birds do not fly.” How would we translate this sentence to have the “some S are not P” form? The first step is to get the descriptions of the two categories using either nouns or noun phrases. The “S” term is easy; it is just “birds” again. But we have to be a bit more careful with the “P” term, since its predicate contains a negation. We do not want any of our categories to contain a negation. Rather, the negation is contained in the form (i.e., the “not”). The category cannot be simply “fly” or even “flies” since neither of these are a category of thing. We have to use our trick of turning the predicate into a noun phrase, i.e., “things that fly.” Given these two category descriptions, we can then translate the sentence to have the categorical form, some S are not P:
Some birds are not things that fly
Again, although the English sounds clunky here, it has the same form as the categorical form, some S are not P, and it allows us to clearly see what the two categories are. To the left is the Venn diagram for this statement.
As noted above, an asterisk on the Venn diagram means that there is at least one thing in that category. By putting the asterisk inside the “birds” category, but outside the “things that fly” category, we are representing that at least one thing that is a bird is not a thing that flies. This is exactly what our original sentence was saying.
Translating categorical statements into their categorical form can be difficult. There is no simple way of doing it other than asking yourself whether your translation accurately captures the meaning of the original English
sentence.
Here is an example of a difficult categorical statement:
Nobody loves me but my mother.
This is a categorical statement, but which of the four categorical forms does it have? The first step is to ask what two categories are being referred to in this sentence. Here are the two categories: “things that love me” and “things that are my mother.” Notice that the category could not just be “my mother” since that is not a category; it is a particular thing. Again, this sounds strange, but it is important to remember that we are describing categories of things. The next question is: what is this sentence saying is the relationship between these two categories? Hint: it has to be one of the four categorical forms (since any categorical statement can be translated into one of these four forms). The sentence is saying that the only things that love me are things that are my mother. The categorical form of the statement is the “all S are P” form. Thus, the sentence, translated into the correct categorical form would be:
All things that love me are things that are my mother.
We will end this section with one last example. Consider the following categorical statement:
The baboon is a fearsome beast.
Which of the four categorical forms does this statement have? Although the article “the,” which often denotes particulars, may lead one to think that this is a particular affirmative form (some S are P), it is actually a universal affirmative form (all S are P). This English sentence has the sense of “baboons are fearsome beasts” rather than of “that (particular) baboon is a fearsome beast.” English is strange, which is what makes translation one of the trickiest parts of logic. So, the two categories are: “baboons” and “fearsome beasts.” Notice that since “fearsome beasts” is already a noun phrase, we do not have to add “things that are…” to it. Using the two category descriptions, the translation into the “all S are P” categorical form is thus:
All baboons are fearsome beasts.
In this section we have learned what categorical statement are, how to translate categorical statements into one of the four categorical forms, and how to construct Venn diagrams for each of the four categorical forms.
3.2 The Venn Test Of Validity For Immediate Categorical Inferences
In the last section, we introduced the four categorical forms. Those forms are below.
We can use Venn diagrams in order to determine whether certain kinds of arguments are valid or invalid. One such type of argument is what we will call “immediate categorical inferences.” An immediate categorical inference is simply an argument with one premise and one conclusion. For example:
Some mammals are amphibious.
Therefore, some amphibious things are mammals.
If we construct a Venn diagram for the premise and another Venn diagram for the conclusion, we will see that the Venn diagrams are identical to each other.
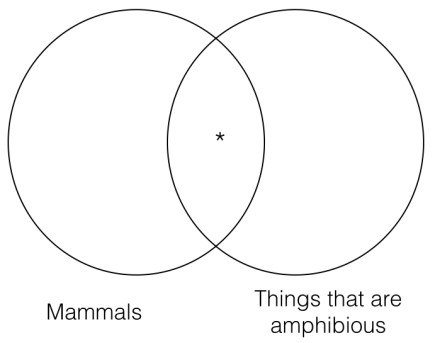
That is, the information that is represented in the Venn for the premise, is exactly the same information represented in the Venn for the conclusion. This argument passes the Venn test of validity because the conclusion Venn contains no additional information that is not already contained in the premise Venn.
Thus, this argument is valid. Let us now turn to an example of an invalid argument.
All cars are vehicles.
Therefore, all vehicles are cars.
Here are the Venn diagrams for the premise and the conclusion, respectively:
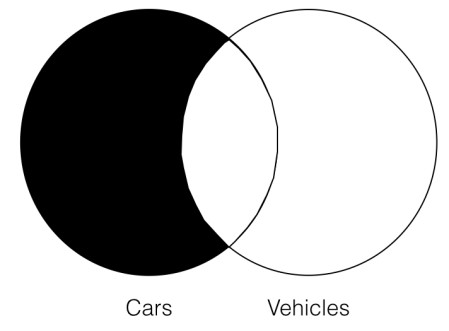
In this case, the Venn diagrams are clearly not the same. More importantly, we can see that the conclusion Venn (on the right) contains additional information that is not already contained in the premise Venn. In particular, the conclusion Venn allows that a) there could be things in the “car” category that are not in the “vehicle” category and b) that there cannot be anything in the “vehicle” category that is not also in the “car” category. That is not information that is contained in the premise Venn, which says that a) there is not anything in the category “car” that is not also in the category “vehicle” and b) that there could be things in the category “vehicle” that are not in the category “car.” Thus, this argument does not pass the Venn test of validity since there is information contained in the conclusion Venn that is not already contained in the premise Venn. Thus, this argument is invalid.
The Venn test of validity is a formal method because we can apply it even if we only know the form of the categorical statements, but do not know what the categories referred to in the statements represent. For example, we can simply use “S” and “P” for the categories—and we clearly do not know what these represent. For example:
All S are P
No P are S
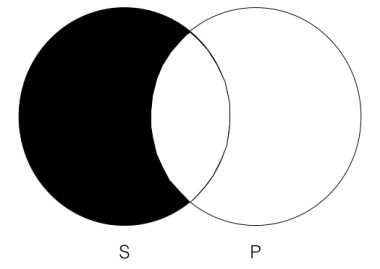
The conclusion (on the right) contains information that is not contained in the premise (on the left). In particular, the conclusion Venn explicitly rules out that there is anything that is both in the category “S” and in the category “P” while the premise Venn allows that this is the case (but does not require it). Thus, we can say that this argument fails the Venn test of validity and thus is invalid. We know this even though we have no idea what the categories “S” and “P” are.
3.3 Venn Validity For Categorical Syllogisms
|
Watch and Learn |
|
Learn about Categorical Syllogism by watching A Crash Course in Formal Logic Pt 6a: Categorical Syllogisms, Terms, Mood and Figure. |
A categorical syllogism is an argument with two premises and a conclusion, where every statement of the argument is a categorical statement. As we have seen, there are four different types (forms) of categorical statement:
All S are P (Universal Affirmative)
No S are P (Universal Negative)
Some S are P (Particular Affirmative)
Some S are not P (Particular Negative)
Thus, any categorical syllogism’s premises and conclusion will be some mixture of these different types of statement. Consider the argument:
All humans are mortal
All mortal things die
Therefore, all humans die.
As we can see now that we have learned the four categorical forms, each one of the statements in this syllogism is a “universal affirmative” statement of the form, “all S are P.” Let us first translate each statement of this argument to have the “all S are P” form:
All humans are things that are mortal.
All things that are mortal are things that die.
All humans are things that die.
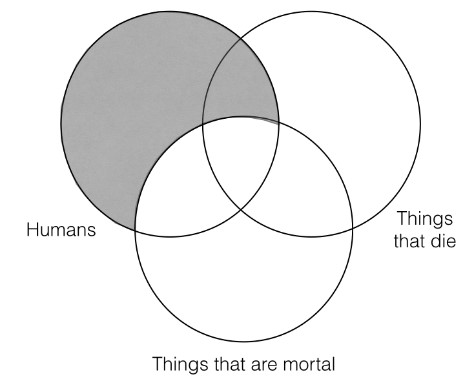
In determining the validity of categorical syllogisms, we must construct a three category Venn diagram for the premises and a two category Venn diagram for the conclusion. To the left is what the three category Venn looks like for the premises.
We need a three category Venn for the premises since the two premises refer to three different categories. The way you should construct the Venn is with the circle that represents the “S” category of the conclusion (i.e., the category “humans”) on the left, the circle that represents the “P” category of the conclusion (i.e., the category “things that die”) on the right, and the remaining category (“things that are mortal”) in the middle, as I have done to the left. Constructing your three category Venn in this way will allow you to easily determine whether the argument is valid.
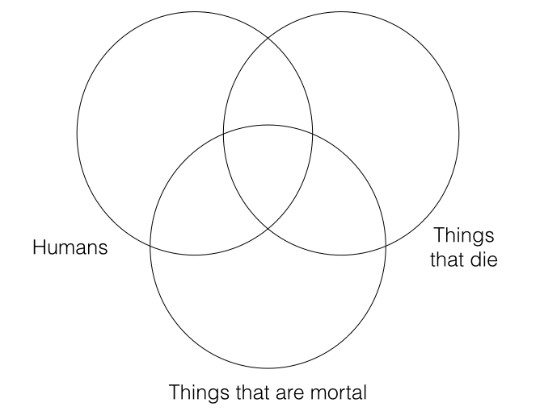
The next thing we must do is represent the information from the first two premises in our three category Venn. We will start with the first premise, which says “all humans are things that are mortal.” That means that we must shade out anything that is in the “human” category that is not in the “things that are mortal” category, as shown in the diagram to the right.
We must then fill in the information for the second premise, all things that are mortal are things that die. That means that there is not anything that is in the category “things that are mortal” that is not in the “things that die” category. So, we must shade out all of the parts of the “things that are mortal” category the lie outside the “things that die” category, as shown below:
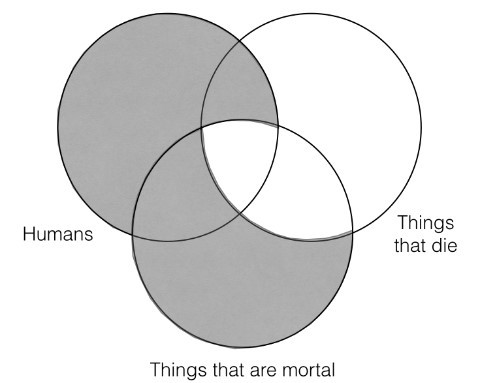
The next thing we have to do is construct a two category Venn for the conclusion and then compare the information represented by the three category Venn for the premises to the two category Venn for the conclusion.
The conclusion represents the information that there is nothing in the “humans” category that is not also in the “things that die” category. It also allows that there are things that die, but that are not humans. The premise Venn also includes this same information, since every part of the “humans” category that is outside the “things that die” category is shaded out. Thus, this argument passes the Venn test of validity and is thus valid since there is no information represented in the conclusion Venn that is not also represented in the premise Venn. Notice that it does not matter that the premise Venn contains more information than the conclusion Venn. That is to be expected, since the premise Venn is representing a whole other category that the conclusion Venn is not. This is perfectly allowable. What is not allowable (and thus would make an argument fail the Venn test of validity) is if the conclusion Venn contained information that was not already contained in the premise Venn. However, since this argument does not do that, it is valid.
Let us try another one.
All pediatricians are doctors
All pediatricians like children
Therefore, all doctors like children.
The first step is to identify the three categories referred to in this categorical syllogism. They are:
Pediatricians
Doctors
Things that like children
The next step is to fill out the three category Venn for the premises and the two category Venn for the conclusion.
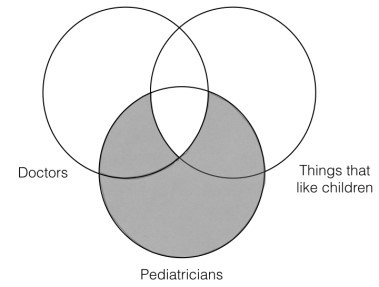
This argument does not pass the Venn test of validity because there is information contained in the conclusion Venn that is not contained in the premise Venn. In particular, the conclusion says that there is nothing in the “doctors” category that is outside the “things that like children category.” However, the premises do not represent that information, since the section of the category “doctors” that lies outside of the intersection of the category “things that like children” is unshaded, thus representing that there can be things there.
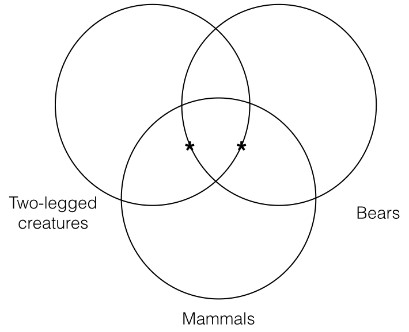
Sometimes when filling in particular statements on a three category for the premises, you will encounter a problem that requires another convention in order to accurately represent the information in the Venn. Here is an example where this happens:
Some mammals are bears
Some two-legged creatures are mammals
Therefore, some two-legged creatures are bears
There are three categories referred to in this categorical syllogism:
Mammals
Bears
Two-legged creatures
As always, we will put the “S” term of the conclusion on the left of our three category Venn, the “P” term on the right, and the remaining term in the middle, as shown to the left.
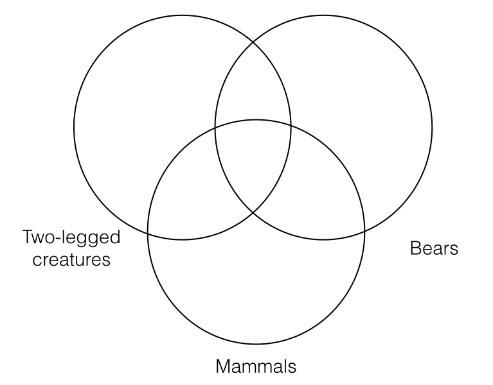
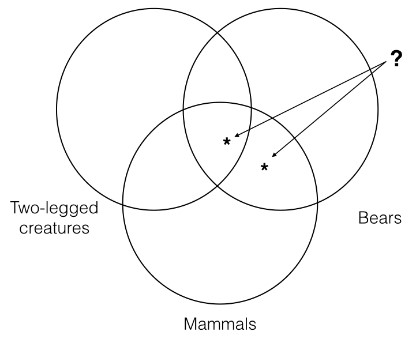
Now we need to represent the first premise, which means we need to put an asterisk in the intersection of the “mammals” and “bears” categories. However, here we have a choice to make. Since the intersection of the “bears” and “mammals” categories contains a section that is outside the “two-legged creatures” category and a section that is inside the “two-legged creatures” category, we must choose between representing the particular as part of the “two-legged creatures” category or not.
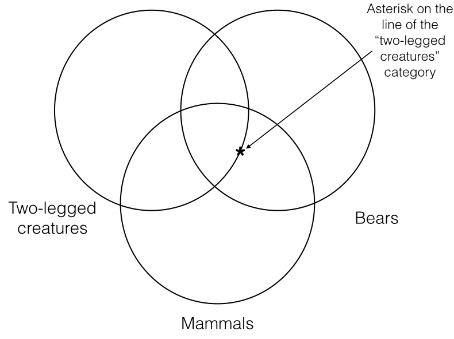
But neither of these can be right, since the first premise says nothing at all about whether the thing that is both a bear and a mammal is two-legged! Thus, in order to accurately represent the information contained in this premise, we must adopt a new convention. That convention says that when we encounter a situation where we must represent a particular on our three category Venn, but the premise says nothing about a particular category, then we must put the asterisk on the line of that category as I have done below. When we do this, it will represent that the particular is neither inside the category or outside the category.
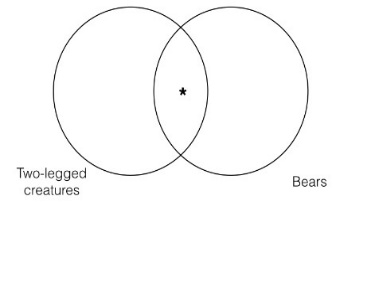
We must do this same thing for the second premise, since we encounter the same problem there. Thus, when putting the asterisk in the intersection of the “two-legged creatures” and “mammals” categories, we cannot put the asterisk either inside or outside the “bears” category. Instead, we must put the asterisk on the line of the “bears” category. Thus, using this convention, we can represent the premise Venn and conclusion Venn as follows:
Keeping in mind the convention we have just introduced, we can see that this argument fails the Venn test of validity and is thus invalid. The reason is that the conclusion Venn clearly represents an individual in the intersection of the “two-legged creatures” and “bears” categories, whereas the premise Venn contains no such information. Thus, the conclusion Venn contains information that is not contained in the premise Venn, which means the argument is invalid.
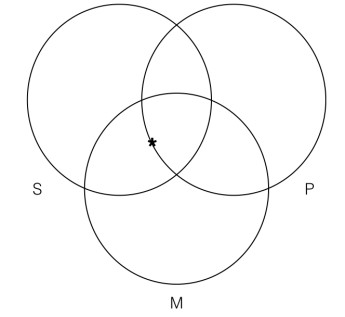
We will close this section with one last example that will illustrate an important strategy. The strategy is that we should always map universal statements before mapping particular statements. Here is a categorical syllogism that illustrates this point. This time I am going to switch to just using the capital letters S, P, and M to represent the categories. Recall that we can do this because the Venn test of validity is a formal evaluation method where we do not have to actually understand what the categories represent in the world in order to determine whether the argument is valid.
Some S are M
All M are P
 Some S are P
Some S are P
If we think about mapping the first premise on our three category Venn, it seems that we will have to utilize the convention we just introduced, since the first premise is a particular categorical statement that mentions only the categories S and M and nothing about the category P:
However, as it turns out, we do not have to use this convention because when we map premise 2, which is a universal statement, this clears up where the asterisk has to go:
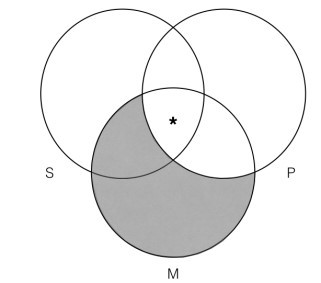
We can see that once we have mapped the universal statement onto the premise Venn (on the left), there is only one section where the asterisk can go that is in the intersection of S and M. The reason is that once we have mapped the “all M are P” premise and have thus shaded out any portion of the M category that is outside the P category, we know that that asterisk cannot belong inside the M category, given that it has to be inside the P category. When we apply the Venn test of validity to the above argument, we can see that it is valid since the conclusion Venn does not contain any information that is not already contained in the premise Venn. The conclusion simply says that there is something that is both S and P, and that information is already represented in our premise Venn. Thus, the argument is valid. The point of strategy here is that we should always map our universal statements onto our three category Venn diagrams before mapping our particular statements. The reason is that the universal can determine how we map our particular statements (but not vice versa).
3.4 The Square of Opposition
|
Watch and Learn |
|
Learn about the Square of Opposition by watching A Crash Course in Formal Logic Pt 5b: Squares of Opposition and their Operations. |
We can also evaluate Categorical Statements using the Square of Opposition. Aristotle was the first to use the Square, and it has proven to be a valuable method to think through arguments based on categorical statements. The following graph illustrates the possible relationships that exist between the four statements.
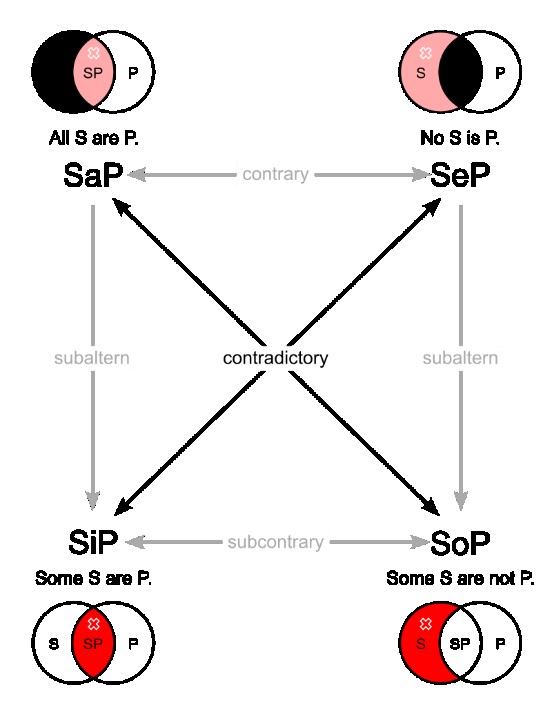
It is important to understand the terms that are used in this Square. First, each of the Categorical Statements is represented by a letter so that:
A = All S are P = Universal Affirmative
E = No S is P = Universal Negative
I = Some S are P = Particular Affirmative
O = Some S are not P = Particular Negative
Aristotle categorized the relationships between these statements in this way.
A and O statements and E and I statements are contradictory. This means that if A is true, the O must be false. If E is true, then I must be false. Conversely, if O is true, then A must be false. If I is true, then E must be false. Statements are contradictory when the truth of one implies the falsity of the other, and conversely. For example, if the statement that
all industrialists are capitalists (A)
is true, then the statement that
some industrialists are not capitalists (O)
must be false. Similarly, if
no mammals are aquatic (E)
is false, then the statement
some mammals are aquatic
must be true.
Secondly, A and E statements are contrary. Statements are contrary when they cannot both be true. For example, if the statement that
all giraffes have long necks (A)
is true, it cannot also be true that
no giraffes have long necks
which is an E Statement. It is important to note, however, that corresponding A and E statements are not contradictory. This is because while they cannot both be true, they can both be false. An example of this would be the fact that the statements
all planets are gas giants (A) AND no planets are gas giants (E)
are both false.
Thirdly, I and O Statements are subcontrary. Statements are subcontrary when it is impossible for both to be false. For example, if the statement
some lunches are free (I)
is false, then the statement
some lunches are not free (O)
must be true. Note, however, that it is possible for corresponding I and O statements both to be true, as with “some nations are democracies,” and “some nations are not democracies.” Again, I and O statements are subcontrary, but not contrary or contradictory.
Lastly, two statements are said to stand in the relation of subalternation when the truth of the first (“the superaltern”) implies the truth of the second (“the subaltern”), but not conversely. “A” statements stand in the subalternation relation with the corresponding “I” statements. For example, the truth of the statement that
all plastics are synthetic (A)
implies the truth of the statement that
some plastics are synthetic (I)
However, the truth of the O Statement that “some cars are not American-made products” does not imply the truth of the E Statement “no cars are American-made products.” The truth of an A or E Statement implies the truth of the corresponding I or O statement, respectively. In the same way, the falsity of an I or O statement implies the falsity of the corresponding A or E statement, respectively. However, the truth of a particular Statement does not imply the truth of the corresponding universal Statement, nor does the falsity of a universal Statement carry downwards to the respective particular Statements.
I know that this may make your head spin for a while when you first read it but in reality, it is a very helpful tool that can help you think about the likely truth or falsity of arguments. So imagine you are in an argument (not the logical type, but the heated variety) with a friend and she says that “you are always late.” If we translate this into a categorical statement, your friend has said, “All arrivals are late.” This is an A statement – All S is P – where S is “you arriving” and P is “late.” How do you demonstrate that your friend’s statement is false? If we look at the Square of Opposition, we can see that the contradictory of A is I. In other words, to prove that A is false, you must prove that I is true. In this case, if you can remember one time you were not late, you have proven her accusation to be false.
Here is another example of how to use the Square of Opposition to determine the truth or falsity of statements. As a general rule, prejudice rests on (usually hidden) universal affirmative and universal negative premises. For example, when someone criticizes how a person is driving by saying “teen drivers,” they are doing so on the basis of a universal affirmative statement that “All teenagers are bad drivers.” Or when someone sees a person wearing a hoodie in a certain neighborhood and assumes they are dangerous, their actions are based on a universal affirmative statement that “All people wearing hoodies in this area are dangerous.” The way to break down this prejudice is to advance the truth of the contradictory.
Understanding subaltern relationships can also help us evaluate arguments. The rule of the subaltern means that:
If A is true, then I is also true.
If A is false, then I is undetermined in truth value.
If I is true, then A is undetermined in truth value.
If I is false, then A is also false.
Politicians frequently fail to observe these logical rules when they advance arguments. They prove “I” and then, on the basis of an “I” statement, advance an argument as if it were an “A” statement. Take the issue of immigration for an example. A political ad will state statistics proving that “Some Illegal Immigrants are Criminals” (Some S is P.) The ad will then go on to argue that we need to stop illegal immigration because illegal immigrants are criminals. The ad makes a subtle shift by implying that the “I” statement supports the truth of a corresponding “A” statement. But the Square of Opposition shows us that this is an invalid inference. “I” statements cannot be used to prove or disprove “A” statements.
This shows us that the Square of Opposition is most helpful in evaluating the inferences people made from categorical statements. To use the Square of Opposition to evaluate inferences, you need to follow the following steps.
Step 1: Determine what kind of a statement it is. A, E, I, or O?
Step 2: Determine whether the statement is true or false.
Step 3: Determine the contradictory of the statement. Remember, since contradictories are always false, the contradictory will be false.
Step 4: Determine the subalternate of the statement and its contradictory. Remember, in the subalternation relationship, falsity flows upward (from below). And also remember that truth flows downward.
Step 5: Determine the subcontrary of the statement and its contradictory. The rule of the subaltern (as defined above) is useful to determine the truth value of the corresponding statements.
Here is a classic example of the steps outlined above with the statement: “All squares are four-sided.”
Step 1: This is an “A” statement – All S is P.
Step 2: This is a true statement.
Step 3: The contradictory of A is O. This means that the statement “Some squares are not four sided” is false.
Step 4: The subalternate of O is E. Since falsity flows upward and since O is false, this means E must also be false. This means that the statement “No squares are four-sided” is also false. The subalternate of A is I. Since truth flows downward, and since A is true, then I must also be true.
Step 5: The subcontrary of O is I. Since only one sub-contrary can be false and since O is false, this means I must be true. “Some squares are four-sided” is thus a true statement.
Following these steps can help us evaluate statements made in commercials, political speeches, and everyday conversation. Understanding logical relationships between statements allows to judge inferences and assumptions in order to know what can (and what cannot) be proven.
3.5 Operations on Categorical Statements
|
Watch and Learn |
|
Learn about Operations on Categorical Statements by watching A Crash Course in Formal Logic Pt 5d: Conversion, Obversion, and Contraposition. |
Another way for us to examine the truth or falsity of categorical statements is to manipulate them in several ways. In this section, we will discuss three different ways known by the names of conversion, obversion, and contraposition. Each of these changes the standard form statements in some way. The question we will ask is whether the new statement that results from the change is equivalent to the original statement; that is, does the new statement express the same proposition as the original? This is important because frequently people making arguments subtly change categorical statements in one of these three ways. It is important to be able to recognize these changes and to evaluate the impact of the change on the truth of the assertion.
Conversion
Performing conversion on a categorical statement involves changing the order of the subject and predicate terms. The result of this operation is a new statement, which is said to be the converse of the original statement. The most important questions to be answered are: When does performing conversion produce a new statement that is equivalent in truth to the first statement? And when does performing conversion change the statement to render it different in truth value from the first?
We will begin by examining “A” categorical statements that propose a universal affirmative (All S are P.). Take for example the statement:
All dogs are animals
Conversion switches the subject and predicate terms, so the converse statement is
All animals are dogs
Does the converse express the same proposition as the original? Are they equivalent? The answer is obviously no. The original statement expresses the true proposition that all dogs are animals; the converse expresses the utterly false proposition that all animals are dogs. Thus, in this example, converting an “A” statement produces a new statement that is not equivalent to the original.
But consider the statement
All unmarried men are bachelors
The converse of this statement is
All bachelors are unmarried men
In this example, the converse is truth equivalent. Both statements are true. This means that the effect on truth-value of converting A statements is unpredictable. Sometimes, as with ‘All dogs are animals’, conversion will lead you from a truth to a falsehood. Other times, it may lead from truth to truth: ‘All bachelors are unmarried men’ and ‘All unmarried men are bachelors’ express different propositions, but both of them are true (because it so happens that, by definition, a bachelor is just an unmarried man). I would also point out that conversion of an “A” statement can also lead from falsehood to falsehood, as with the transition from ‘All dogs are bats’ to ‘All bats are dogs’. And it could lead from falsehood to truth: just reverse the order of the first conversion we looked at, from ‘All animals are dogs’ to ‘All dogs are animals’. The most important point here is that, because conversion of A statements produces a converse that expresses a different proposition than the original, we cannot know what the effect of the conversion will be on truth-value.
What happens when we apply conversion to universal negative “E” propositions? Take the statement
No dogs are cats
Its converse would then be
No cats are dogs
Are they equivalent? Yes they are. Remember, an E proposition denies even partial inclusion; it makes the claim that the two classes involved do not have any members in common. It does not matter which of the two classes is listed first in the statement expressing that proposition—you still get the assertion that the two classes are exclusive. Thus, when you perform conversion on E statements the new statement that is equivalent to the original.
This is also true of particular affirmative “I” statements. For example, the statement
Some sailors are pirates
after conversion, becomes
Some pirates are sailors
Notice that these two statements express the same proposition: they make the claim that the two classes have at least one member in common—there is at least one thing that is both a sailor and a pirate. Again, it does not matter what order you put the class terms in. An “I” statement and its converse are always equivalent.
Finally, we can consider particular negative “O” statements. Consider the statement
Some human beings are not professors
That expresses a true proposition. But note that its converse
Some professors are not human beings
expresses a different idea which is obviously false. That is all we need to show that an operation does not produce equivalent statements: one counterexample. As above with “A” statements, this means that the effect on truth-value of converting O statements is unpredictable. It can take us from truth to falsehood, as in this example, or from truth to truth, falsehood to falsehood, falsehood to truth. In the abstract, we cannot know the effect on truth of converting O statements, since the converse expresses a different proposition from the original.
Thus, in summary, when applying conversion to categorical statements:
for E and I, converses are equivalent
for A and O, converses are not equivalent
Obversion
To understand the next way in which categorical statements can be changed, we need to introduce a new concept: class complements. The complement of a class is another class which contains all the things that are not members of that class. For example, the complement of the class of cats is everything that exists that is not a cat. The easiest way to name class complements is just to stick the prefix ‘non’ in front of the original class name. So the complement of cats is non-cats. As a matter of notational convention, if we use a capital letter like S to refer to a class, we will denote the complement of that class as ~ S, which we will read as “tilde-S.”
This is important to remember as we move to talk obversion. When you obvert a statement, you begin by changing the statement from affirmative to negative or from negative to position. Then, you replace the predicate with its complement. The result of performing obversion on a statement is called the obverse of the original.
It turns out that performing obversion on a statement always produces a new statement that is equivalent in meaning and truth-value to the original. A statement and its obverse are thus always equivalent. That means they share a truth-value: if the original statement is true, so is its obverse; if the original statement is false, its obverse is false, too. To illustrate this, Let uslook at the impact of obversion on all four categorical statement types.
Consider the statement
All penguins are swimmers.
To perform obversion on this statement, we first change its quality. This is a universal affirmative. Its quality is affirmative. So we change that to negative, keeping the quantity (universal) the same. Our new statement will be a universal negative “E” statement (No S are P). The first step thus produces the statement
No penguins are swimmers.
But this is not the obverse. To complete the obversion process, we must replace the predicate with its complement. The predicate of the statement is ‘swimmers’. What’s the complement of that class? All the things that are not swimmers: non-swimmers. So the obverse of the original A statement is this:
No penguins are non-swimmers.
Are these two statements equivalent? Absolutely.
All penguins are swimmers
expresses the universal affirmative statement, asserting that the class of penguins is entirely contained in the class of swimmers. That is to say, any penguin you find will also be in the swimmer class. Another way of putting it: you will not find any penguins who are not in the class of swimmers. In other words, no penguins fail to be swimmers. This is expressed in the E categorical statement No penguins are non-swimmers.
Thus, the A statement and its obverse are equivalent; they express the same idea, make the same claim about the relationship between the class of penguins and the class of swimmers.
Next we can apply obversion to a universal negative “E” statement. Consider the statement
No cats are birds
To obvert this statement, change its quality from negative to affirmative, so that it becomes a universal affirmative “A” statement (i.e., All S are P). We then replace the predicate ‘birds’ with its complement, ‘non-birds’. The result is the statement
All birds are non-cats.
Is that equivalent to the original? It tells us that all birds are outside the class of cats. In other words, none of them are cats. Both the original statement and its obverse tell us that the classes of cats and birds are exclusive.
We can look at particular affirmative “I” statements. For example, consider the statement
Some politicians are Republicans.
To obvert this statement, we first change the quality—from affirmative to negative, so that it is
Some politicians are not Republicans.
We have one more step to complete the obversion process. The word ‘Republicans’ should be replaced with ‘non-Republicans.” (Note: it is a mistake to change Republicans to Democrats because there are many who are not Republican or Democrat.) The obverse statement is thus:
Some politicians are not non-Republicans.
Granted, this is a convoluted English sentence, but the meaning is clear: not being a non-Republican is just being a Republican. This says the same are the original, namely that some politicians are Republicans.
Finally, consider the particular negative “O” statements. For example, consider the statement
Some plants are not flowers
We begin by changing from negative to affirmative so that it becomes an “I” statement (Some S are P). We then replace ‘flowers’ with ‘non-flowers’ so that the full obversion process leads to the statement
Some plants are non-flowers
We went from ‘Some plants are not flowers’ to ‘Some plants are non-flowers’. Obviously, these two statements are equivalent.
Thus, in summary, when applying conversion to categorical statements:
- Obverses are equivalent for A, E, I, and O statements
Contraposition
Our last operation is contraposition. Unlike obversion, and like conversion, it does not involve changing the type (A, E, I, O) of the statement. Rather, again, like conversion, we just change the subject and predicate. This is the process we follow. Replace the subject with the complement of the predicate. Then replace the predicate with the complement of the subject. The result of performing contraposition on a statement is called its contrapositive.
Here is how to perform contraposition on the “A” statement
All women are mortals
To form its contrapositive, we put the complement of the predicate—non-mortals—into the subject position and the complement of the subject—non-men—into the predicate position so that it becomes
All non-mortals are non-women.
The question, as always: are these statements equivalent? The answer is yes. (This can be proved by using the Venn Diagram method.) When we perform contraposition on universal affirmative “A” statements the new statements express the same proposition as the original. Thus, an “A” statement and its contrapositive are equivalent.
We can perform the same process on a universal negative “E” statement like
No skydivers are cowards
To find the contrapositive of this statement, we replace the subject, skydivers, with the complement of the predicate, non-cowards; and we replace the predicate, cowards, with the complement of the subject, non-skydivers. The result is
No non-cowards are non-skydivers.
We immediately can see that this is a false statement. If we think about the brave human beings who have lived, many of them lived before planes and thus were not skydivers. Thus, the contrapositive claim there is no such thing as a non-coward who does not sky-dive is false. In general, when you perform contraposition on an E statement, you end up with a new statement that expresses a different statement with an unpredictable truth value. You may move from truth to falsehood, as in this case, or from truth to truth, falsehood to falsehood, falsehood to truth. Contraposition changes the proposition expressed by E statements, thus affecting its truth value.
Next, we can consider particular negative (O) statements. Consider the statement
Some men are not NFL players
Performing contraposition, the statement becomes
Some non-NFL players are not non-men
Things that are “not non-men” are men. So the claim being made by the contrapositive is that some non-NFL players are men. That is, there is at least one thing that’s both a non-NFL player and a man; or, there is at least one man who’s not a NFL player. Thus, the O statement and its contrapositive make the same claim. Thus, we can conclude that contraposition performed on particular negatives gives you a new statement that is equivalent to the original.
Finally, consider a particular affirmative “I” statement like
Some women are professional soccer players
This statement is true. So is its contrapositive:
Some non-professional soccer players are non-women
Since I am a non-woman and a non-professional soccer player, this statement is true. But this is not always the case. Consider the particular affirmative “I” statement
Some Catholics are non-Popes
That’s certainly true. The contrapositive of this statement would be
Some Popes are non-Catholics (note: the complement of non-Popes is Popes).
This is statement is obviously false. All Popes are Catholic because being a Catholic is a prerequisite for the Papacy. In this instance, the “I” statement and its contrapositive make different claims. Thus, we can conclude that the equivalence of “I” statements and their contrapositives are indeterminate.
Thus, in summary, when applying contraposition to categorical statements:
“A” and “O” statements and their contrapositives are equivalent
“E” and “I” statements and their contrapositives are not equivalent
|
Chapter Review |
|
Review what you have learned in this chapter about Categorical Logic by watching the following short videos: |