Índice
- Introducción
- Determinación del Centro de Masa
- Estudio de los posibles movimientos de un Cuerpo Rígido (CR) en un plano perpendicular a su eje de simetría
- Condición de rigidez
- Casos particulares de movimientos de CR
- Diagramas vectoriales
- Centro instantáneo de rotación (CIR)
- Aplicaciones de cinemática del CR
Cinemática del Cuerpo Rígido (CR)
1_INTRODUCCIÓN
Consideramos hasta ahora, en forma general, el modelo mecánico de sistemas de partículas. El enfoque inicial de mecánica clásica de sistemas de partículas, no pretende reconocer cómo están constituidos los sistemas de puntos materiales sobre los cuales se aplica.[1]
Continuaríamos nuestro avance en el estudio de sistemas de partículas haciendo uso de otros enfoques de la mecánica clásica, por ejemplo, investigando los grados de libertad y la utilización de coordenadas generalizadas para describir la evolución del sistema, pero esta forma no es tan sencilla desde el punto de vista matemático y se desarrollará específicamente en cursos de Mecánica Analítica o Racional.
Los sistemas de partículas tales como los fluidos incompresibles y los cuerpos rígidos (sin pretender indagar en la física del sólido ni en la física del líquido) podemos estudiarlos desde el punto de vista de la mecánica clásica como sistemas continuos. También nos permitiremos tomar un sistema discreto, masas puntuales unidas o vinculadas por varillas inextensibles e inflexibles, como aproximación a cuerpos rígidos.
Una puerta de posible acceso a esta modalidad de la mecánica se nos abre si logramos establecer condiciones constitutivas o “leyes” constitutivas que aceptaremos como válidas en cada tipo de sistemas de partículas.
Elegiremos las leyes constitutivas que caracterizan cada sistema en particular, con mucho cuidado para que sean lo más sencillas posibles y que puedan tomarse arbitrariamente para cualquier subconjunto de partículas del sistema.
Distingamos entonces entre los sistemas de partículas aquellos a los que llamaremos “rígidos”. Es decir, aquellos sistemas de partículas que cumplen las leyes universales de la mecánica de los sistemas y además las leyes constitutivas del sistema rígido.
Proponemos que un sistema es rígido si al considerar dos partículas cualesquiera de él se verifica que la distancia entre dichas partículas es un invariante, sin importar las interacciones externas o internas que soporten las partículas.
Ejemplo: si la partícula “A” está a 10 [cm] de distancia de la partícula “B”, lo seguirá estando siempre no importa el movimiento que realice el sistema o las interacciones a las cuales esté sometido. Recordemos que la distancia es una magnitud escalar. Si suponemos el punto “A” como fijo, al punto “B” lo podemos mover sobre un arco de circunferencia centrada en “A”.
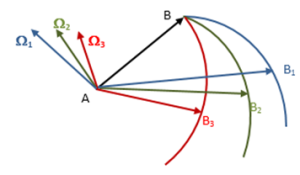
La figura representa tres arcos de círculo máximo de una superficie esférica de radio iguales aunque por la perspectiva parezcan diferentes.
Dibujamos tres movimientos posibles del punto B (a Bi) relativo al punto A, uno en cada plano, normal al correspondiente vector . En cada caso el punto B pasa de la posición inicial a la posición final (se suponen arcos pequeños recorridos en intervalos pequeños de tiempo):
Ω1: de B → B1
Ω2: de B → B2
Ω3: de B → B3
El arco de circunferencia puede estar en cualquier plano del espacio euclídeo 3D o R3.
Para expresar esta condición respecto de un sistema de referencia fijo al laboratorio en el punto “O”, podemos decir que:
VA-O velocidad de “A” respecto del laboratorio
VB-O velocidad de “B” respecto del laboratorio
VB-A velocidad de “B” respecto de A
La velocidad del punto “B” respecto de “A” en un cuerpo o sistema rígido es una rotación de “B” alrededor de “A” (recordemos que la distancia de “B” respecto de “A” es constante), entonces:
[latex]\vec{v}_{B-A}=\vec{\Omega} \times \vec{r}_{B-A}[/latex]
Teniendo en cuenta lo que vimos en movimiento relativo, la ecuación expresa la velocidad relativa del punto “B” respecto del punto “A”.
También si consideramos que el punto “A” tiene una cierta velocidad respecto del laboratorio, velocidad a la que podemos identificar como velocidad de arrastre, la velocidad del punto “B” respecto del laboratorio será la suma vectorial de “arrastre” más relativa:
[latex]\vec{v}_{B-O}=\vec{v}_{A-O}+\vec{\Omega} \times \vec{r}_{B-A}[/latex]
En lo que sigue desarrollamos con más cuidado el significado físico de esta ecuación, que se conoce como ecuación de la roto-traslación del CR.
Rotar y trasladarse es el movimiento más general que puede hacer un cuerpo rígido, ya que si se dilatase, distorsionase o deformase por flexión, no sería un CR.
En realidad no existen los cuerpos indeformables. Todo cuerpo bajo la acción de un sistema de fuerzas se deforma y/o se mueve. Puede no moverse, pero entonces necesariamente se deforma bajo la fuerza de presión o torque actuante. Pero podemos aplicar el modelo del CR, cuando las deformaciones que se producen, debido a la acción del sistema de fuerzas aplicado al cuerpo en estudio las podemos despreciar.
Para simplificar el tratamiento matemático del tema trabajaremos solamente con cuerpos isótropos y homogéneos, y con forma de un cuerpo geométrico plano con eje de simetría (cuerpo de revolución) o varillas de caras perfectamente planas y de sección constante. De estos cuerpos sólo se estudiarán rotaciones en un plano normal o paralelo al eje de simetría.
Así limitados los casos que se van resolver, comenzaremos a desarrollar el modelo propuesto.
2_DETERMINACIÓN DEL CENTRO DE MASA (CM) DEL CUERPO RÍGIDO
Un punto notable del Cuerpo Rígido es el Centro de Masa. Para preparar el estudio de sus aplicaciones, comenzamos por determinar su posición.[2] Tal como definimos la posición del CM para un sistema de partículas:
[latex]\vec{r}=\frac{\sum_{i=1}^{n}m_{i}r_{i}}{M}\[/latex]
Ahora como el CR continuo tiene muchas partículas y es un medio isótropo y homogéneo, es decir la densidad “ρ”[3] permanece constante, la masa elemental se transforma en un diferencial de masa y se puede reemplazar por el producto de la densidad por un diferencial de volumen, es decir y la sumatoria se transforma en una integral. El CM de un CR lo podemos calcular entonces como:
[latex]\vec{r}_{cm}=\frac{\int \vec{r}\, dm}{M}[/latex]
[latex]\vec{r}_{cm}=\frac{\rho \int \vec{r}\, dV}{M}[/latex]
Debemos hacer notar que la integral a lo largo de todo el volumen es una integral triple y que la ecuación vectorial del centro de masa de un CR deriva en tres ecuaciones escalares:
[latex]X_{CM}=\frac{\rho \int x dV}{M}[/latex]
[latex]Y_{CM}=\frac{\rho \int y dV}{M}[/latex]
[latex]Z_{CM}=\frac{\rho \int z dV}{M}[/latex]
3_ ESTUDIO DE LOS POSIBLES MOVIMIENTOS DE UN CUERPO RÍGIDO EN UN PLANO PERPENDICULAR A SU EJE DE SIMETRÍA
Movimiento general de roto-traslación
Laroto–traslacióneselmovimientomásgeneralquepuedetenerunCR que se mueve en un plano normal a un eje de simetría. Esta restricción sobre el eje de simetría la hacemos pues estamos desarrollando un estudio elemental de la cinemática del cuerpo rígido. De cualquier modo la roto-traslación se puede considerar como movimiento general.
Un ejemplo típico de este movimiento lo constituye la Tierra que se traslada en una órbita elíptica alrededor del Sol y simultáneamente gira en torno a un eje que pasa por los polos. En realidad sólo es posible considerar a la Tierra como un CR en una primera aproximación ya que debido a las mareas, los movimientos por interacción gravitatoria, el desplazamiento de las placas tectónicas, etc, no es estrictamente un sólido rígido.
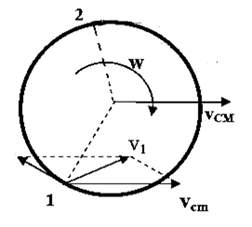
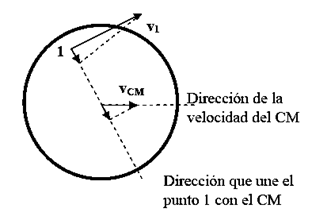
Si un CR se mueve como se muestra en la figura con una velocidad de traslación y al mismo tiempo rota con velocidad angular , la velocidad de un punto como el 1 se obtiene sumando geométricamente la , y la velocidad de rotación del punto 1 alrededor del CM cuya dirección es perpendicular a la que une el CM con el punto 1.
Hemos visto que la roto – traslación de un CR se puede considerar como una superposición de una traslación del CM con una rotación alrededor del CM. Por esta razón cuando se expresa la velocidad de un punto cualquiera en función del CM, estamos considerando al CM como centro de reducción. Pero, desde el punto de vista cinemático exclusivamente ¿El CM es un punto tan especial?
Si expresamos la velocidad de dos puntos del CR tomando al CM como centro de reducción:
[latex]\vec{v}_{1}=\vec{v}_{CM}+\vec{\Omega} \times \vec{r}_{1-CM}[/latex] (1)
[latex]\vec{v}_{2}=\vec{v}_{CM}+\vec{\Omega} \times \vec{r}_{2-CM}[/latex]
Si ahora restamos estas dos igualdades miembro a miembro:
[latex]\vec{v}_{1}-\vec{v}_{2}=\vec{\Omega} \times (\vec{r}_{1-CM}-\vec{r}_{2-CM})[/latex]
La resta que está entre paréntesis la podemos indicar como y la podemos expresar como . De acuerdo a esta fórmula, la velocidad del punto 1 podemos expresarla tomando al punto 2 como centro de reducción. Entonces cualquier punto del CR se puede tomar como centro de reducción. Que generalmente se elija el CM, no significa que cambia la expresión cinemática obtenida anteriormente.
Cuando trabajamos con el modelo de SP cada una de ellas podía tener cualquier velocidad, porque cada partícula se mueve independientemente de las otras que conforman el sistema. ¿Es lo mismo en el cuerpo rígido?
Por lo dicho en la introducción sospechamos que no, pero ampliemos esta idea.
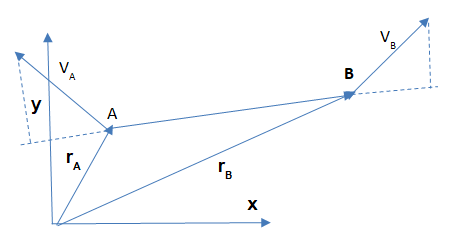
Observamos que en el caso de un CR las componentes o proyecciones de las velocidades de A y de B, en la dirección que las une, deben ser iguales. ¿Por qué? Porque si no los puntos A y B se separarían y esto es imposible por la definición del modelo.De la expresión (1) podemos encontrar la aceleración de un punto del CR, por ejemplo el punto “2” de la figura 4, en función de otro punto (en particular del CM).
Si en cambiodeseamosencontrarla aceleración porejemplo delpunto2, hay que sumar geométricamente tres vectores como se muestraen la figura 4.
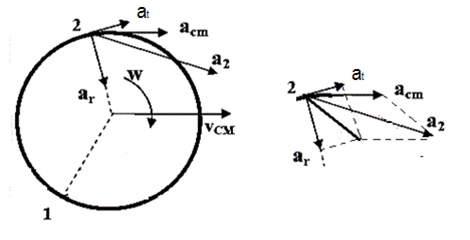
[latex]\vec{a}_{t}[/latex]= aceleración transversal
[latex]\vec{a}_{r}[/latex]= aceleración radial
[latex]\vec{a}_{2}[/latex]= (aceleración de “2” respecto del LAB)
[latex]\vec{a}_{1}=\vec{a}_{CM}+\vec{\gamma }\times \vec{r}_{1-CM}+\vec{\Omega }\times \vec{v}_{1-CM}[/latex]
Donde es la velocidad relativa del punto 1 respecto del CM. Como esta corresponde a una rotación pura podemos escribirla como . Entonces:
[latex]\vec{a}_{1}=\vec{a}_{CM}+\vec{\gamma }\times \vec{r}_{1-CM}+\vec{\Omega }\times (\vec{\Omega }\times \vec{r}_{1-CM})[/latex]
[latex]\vec{a}_{CM}[/latex] es como la aceleración de arrastre del punto de reducción,la [latex]\vec{a}_{t}[/latex] (transversal[4]) en dirección perpendicular a la que une el CM con el punto 2 y la [latex]\vec{a}_{r}[/latex] en la dirección radial y hacia el CM.
4_ CONDICIÓN DE RIGIDEZ
Son muchas las condiciones que pueden expresar la condición de rigidez del modelo. Por ejemplo, Ω y γ deben ser únicos para todos los puntos del CR. A estas condiciones le agregamos ahora que las proyecciones de las velocidades de dos puntos A y B cualesquiera de un CR en la dirección que los une deben ser iguales para que se mantenga invariante la distancia entre ellos.
El centro de reducción, como ya dijimos, para expresar las velocidades del CR puede ser cualquiera. Pero, la rigidez le impone al CR una condición que permite resolver problemas cuando se tienen pocos datos.
Esta condición de rigidez puede expresarse también de otro modo. Sean A y B los puntos del cuerpo en consideración, la velocidad relativa de los mismos debe ser perpendicular a la dirección que une los puntos A y B.
Es decir: [latex](\vec{v}_{A}-\vec{v}_{B})\cdot (\vec{r}_{A}-\vec{r}_{B})=0[/latex]
Aplicando la propiedad distributiva del producto respecto a la suma [latex]\vec{v}_{A}\cdot (\vec{r}_{A}-\vec{r}_{B})=\vec{v}_{B}\cdot (\vec{r}_{A}-\vec{r}_{B})[/latex] . Como el módulo o norma del producto escalar es el producto de los módulos por el coseno del ángulo comprendido entre los vectores dados:
[latex]\vec{v}_{A}\cdot \left |\vec{r}_{A}-\vec{r}_{B} \right | cos \alpha =\vec{v}_{B}\cdot \left |\vec{r}_{A}-\vec{r}_{B} \right | cos \beta[/latex]
Simplificando la expresión obtenemos que:
[latex]\vec{v}_{A} cos \alpha =\vec{v}_{B} cos \beta[/latex]
Esto no es otra cosa que la igualdad de las proyecciones de las velocidades de A y de B en la dirección que une los dos puntos.
Esta es la condición de rigidez que se considerará como característica más importante cuando se hable de un cuerpo rígido.
5_CASOS PARTICULARES DE MOVIMIENTOS DE CR
Se presentan diferentes movimientos de un cuerpo rígido y que podemos considerar como casos particulares de la ecuación (1).
a) Traslación Pura en R3
El movimiento más sencillo que puede tener un CR es el de traslación pura.
Un CR se mueve con traslación pura, cuando todos los puntos del mismo,en cada instante,tienen la misma velocidad y la misma aceleración.
De (1) la velocidad del punto 1 es: . Si generalizamos y escribimos para un punto cualquiera i del CR:
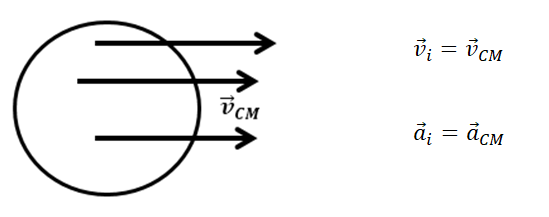
Esta traslación puede implicar, en general, una trayectoria curvilínea y la aceleración tendrá entonces componentes normal y tangencial. Las trayectorias de los distintos puntos del rígido en traslación son tales que, en cada instante, las rectas tangentes correspondientes tienen idéntica pendiente en todos ellos. Pero la pendiente puede cambiar instante a instante, si se trata de una trayectoria curvilínea.
b) Rotación Pura (en R3)
El movimiento de un CR es de rotación pura si, por lo menos, dos de sus puntos tienen velocidad nula (eje de rotación) y los restantes puntos del mismo realizan movimientos circulares alrededor del eje de rotación. Es decir, que si hay más de dos puntos con velocidad nula, éstos deben estar alineados. Si hubiera tres puntos fijos no alineados, ese rígido permanecerá fijo. Las trayectorias de cada punto del cuerpo son circunferencias concéntricas, en un plano normal al eje, con su centro en el eje fijo; la velocidad de cada punto del cuerpo tendrá una dirección tangente a su trayectoria, es decir, perpendicular a la posición de esa partícula con respecto al eje de rotación.
En R2 podemos decir que el eje de rotación queda representado sobre un punto.
Veremos más adelante que se lo denomina centro de rotación y si la rotación se verifica instantáneamente se lo llama centro instantáneo de rotación (CIR).
El caso más común es que el eje de rotación coincida con un eje de simetría del CR.
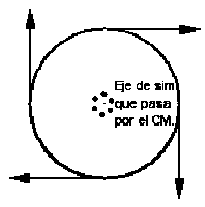
Como el movimiento de los puntos es circular, podemos escribir para una partícula [latex]\vec{v}_{i}=\vec{\Omega } \times \vec{r}_{i-CM}[/latex] .
En esta ecuación es la velocidad de un punto cualquiera del CR y Ω es la velocidad angular de todos los puntos del cuerpo. Esta velocidad es constante, ya que si no lo fuera el cuerpo se deformaría. Por último ri-CM es la posición de un punto cualquiera respecto del CM.
La aceleración de un punto genérico i en este caso es:
[latex]\vec{a}_{i}=\vec{\gamma} \times \vec{r}_{i-CM}+\vec{\Omega } \times \vec{r}_{i-CM}[/latex]
(válida para algún eje de rotación que pase por el centro de masa, que permanece sin trasladarse por el Laboratorio).
Observemos que el 1º término puede ser cero pero la aceleración normal (aquí el término normal se refiere al versor normal que tiene igual dirección pero es opuesto al versor radial) es siempre distinta de cero, para todos los puntos que no están en el eje de rotación. Para los puntos del eje la aceleración normal es cero ya que [latex]\vec{r}_{CM-CM}=\vec{0}[/latex].
6_DIAGRAMAS VECTORIALES
En las carreras de ingeniería se utilizan comúnmente diagramas vectoriales que nos permiten visualizar rápidamente la situación de interés. En la cinemática del CR se pueden utilizar diagramas vectoriales para facilitar el estudio del movimiento del CR.
Diagramas característicos de la traslación
Tratamos representar las velocidades y/o aceleraciones de los infinitos puntos de un diámetro. Elegimos el diámetro marcado en línea punteada que permanecerá paralelo a sí mismo durante el movimiento, pues ejemplificamos traslación pura respecto del laboratorio.
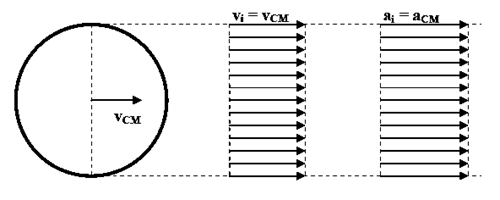
Elegimos un diámetro perpendicular a la velocidad del CM. Todos los puntos de ese diámetro tienen velocidades paralelas a la velocidad del CM. Por eso podemos representarlo fácilmente. Lo mismo ocurre con la aceleración.
Decimos entonces que los diagramas vectoriales característicos de la traslación pura son rectangulares. Si un CR tiene diagramas vectoriales rectangulares de velocidad y/o de aceleración, se mueve con traslación pura.
Diagramas característicos de la rotación pura
Representamos a continuación, las velocidades y/o aceleraciones de los infinitos puntos de un diámetro.
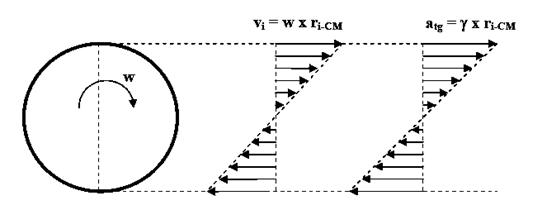
OBSERVACIÓN: En este caso la aceleración que hemos podido representar; NO ES la aceleración total de los puntos del diámetro elegido, sino solamente la aceleración transversal (falta la aceleración normal).
Con esta salvedad, diremos que los diagramas vectoriales de la rotación pura son doble triangulares y simétricos. De la misma manera, si los diagramas del movimiento del CR son doble triangulares y simétricos, el cuerpo está animado de un movimiento de rotación pura.
Diagramas característicos de la roto – traslación
A continuación, con el principio de superposición, dibujamos los diagramas vectoriales característicos de la roto – traslación como la suma de una traslación y una rotación pura (tanto para velocidades como para aceleraciones).
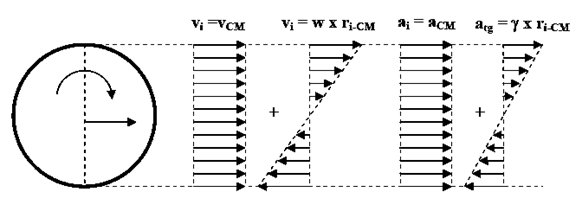
OBSERVACIÓN!!! Nuevamente recordemos que la suma de estas aceleraciones no da por resultado la aceleración total de un punto del CR pues falta la aceleración normal que, en cada caso, es perpendicular a la aceleración tangencial. La suma vectorial de las tres componentes sí da por resultado dicha aceleración total.
El resultado de estas superposiciones dependerá de las normas o intensidades de los vectores que se suman. En este sentido existen 3 casos posibles:
1° Caso: La velocidad de traslación es de mayor intensidad que la de rotación. (Se traslada más rápido de lo que rota).
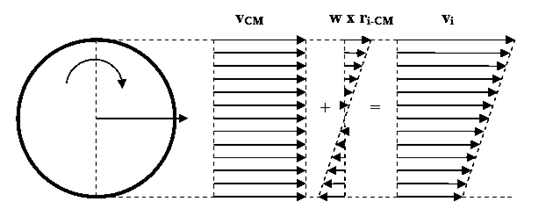
El diagrama vectorial característico de velocidades de la roto – traslación cuando el CR se traslada más rápido de lo que rueda, es trapezoidal. Si el cuerpo se mueve respecto del piso, la velocidad del punto de contacto tiene el sentido de la velocidad de traslación. Esto significa que el cuerpo deslizaría en el sentido de la traslación y la fuerza de rozamiento que se pone de manifiesto es la fuerza de rozamiento dinámica que se opone al deslizamiento entre ambas superficies.[5]
Esta situación podría utilizarse para modelizar una rueda de un automotor que no tenga sistema ABS, anti bloqueo de frenado, cuando intenta frenar y comienza a deslizar con la rueda semibloqueada.
2° Caso: El cuerpo tiene mayor velocidad de rotación que de traslación (el cuerpo rota más rápido de lo que se traslada).
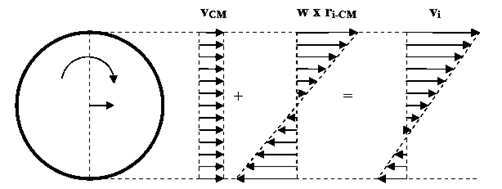
El diagrama vectorial característico de velocidades de la roto – traslación cuando el CR rota más rápido de lo que se traslada, es doble triangular asimétrico. Si el cuerpo se mueve respecto del piso la velocidad del punto de contacto tiene sentido contrario a la velocidad de traslación. Esto significa que el cuerpo desliza en el sentido opuesto de la traslación y, la fuerza de rozamiento que se pone de manifiesto es la fuerza de rozamiento dinámica.
Esta situación podría utilizarse para modelizar una moto cuya rueda trasera tiene un exceso de aceleración. La rueda está “arando” según términos habituales de la calle.
3° Caso: Rodar sin deslizar. En este caso la velocidad de traslación es exactamente igual a la de rotación.
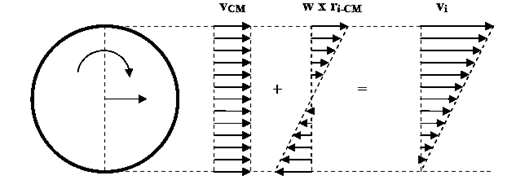
El diagrama vectorial característico de velocidades de la roto – traslación cuando el CR rueda lo mismo que lo que se traslada, es triangular. En este caso el punto de contacto tiene velocidad relativa a la superficie de apoyo nula. Esto significa que el cuerpo no desliza en ningún sentido. La fuerza de rozamiento que se pone de manifiesto es la fuerza de rozamiento estática y puede valer cero. ¿Podría el cuerpo rodar sin deslizar y la velocidad del punto de contacto respecto de Tierra ser distinta de cero?
7_CENTRO INSTANTÁNEO DE ROTACIÓN (CIR)
Si comparamos los tres diagramas obtenidos y se extrapolan fuera del CR:
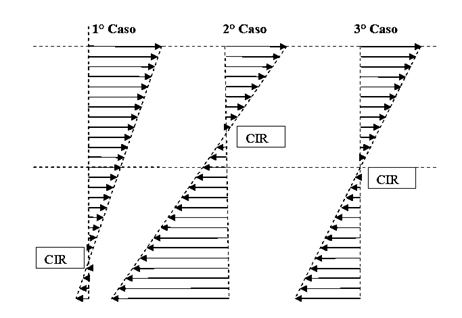
Observamos que los tres diagramas pueden considerarse doble – triangulares. Los diagramas doble – triangulares son característicos de la rotación pura. El eje de rotación tiene velocidad nula. El punto de velocidad cero lo denominamos Centro Instantáneo de Rotación.
8_APLICACIONES DE CINEMÁTICA DEL CR
1.- Dados el radio R = 0,30 m de un cuerpo rígido, la velocidad del centro de masas [latex]\vec{v}_{CM}=-10 \frac{m}{s}\breve{j}[/latex] y el módulo y dirección de la velocidad de un punto P del mismo como se indica en la figura [latex]\left |{v}_{P} \right |=20 \frac{m}{s}[/latex] a 60º de la vertical.
Encontrar la velocidad angular con que se mueve el cuerpo, el CIR y la velocidad del punto Q que se indica en la figura.
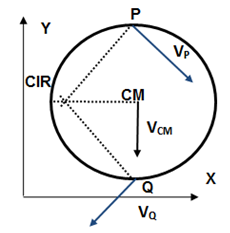
Analizando la figura podemos afirmar que como el CIR es un punto respecto del cual el CR se mueve con rotación pura, debe estar en la intersección de las perpendiculares a las velocidades dadas de dato. Por lo tanto, el sentido de rotación del cuerpo tiene que ser horario.
Elegiremos un sistema de referencia inercial y un sistema de coordenadas cartesiano ortogonal con origen en un punto fijo al LAB, como indica la figura anterior.
Como tenemos la velocidad de dos puntos estudiaremos primero si se cumple la condición de rigidez. La velocidad del CM en “y” debe coincidir con la componente de la velocidad de P en ese eje.
[latex]{v}_{CM} ={v}_{P} cos (60^{\circ})[/latex]
[latex]10\frac{m}{s} =20\frac{m}{s} cos (60^{\circ})[/latex]
y esto se cumple.
Encontremos el radio del CR
[latex]\vec{v}_{P}=\vec{v}_{CM}+\vec{\Omega }\times \vec{r}_{P-CM}=(-10\frac{m}{s})\check{j}+\begin{vmatrix} i &j &k \\ 0& 0& \Omega \\ 0& R& 0 \end{vmatrix}[/latex]
Igualando componente a componente
[latex]\vec{\Omega }=57,7 \frac{1}{s}\breve{k}[/latex]
¿Cómo calculamos analíticamente la posición del CIR? Teniendo en cuenta que el CM describe una rotación pura alrededor del CM.
[latex]\vec{v}_{CM}=\vec{\Omega } \times \vec{r}_{CM-CIR}[/latex]
[latex]-10\frac{m}{s}\check{j}=\begin{vmatrix} i &j &k \\ 0& 0& \Omega \\ -x_{CIR}& -y_{CIR}& 0 \end{vmatrix}[/latex]
igualamos componente a componente
[latex]10\frac{m}{s}=x_{CIR}\Omega[/latex]
[latex]0=y_{CIR}[/latex]
[latex]\vec{r}_{CIR}=(0,173;0;0)[/latex]
Finalmente la podemos hallarla suponiendo que el punto Q describe una rotación pura alrededor del CIR.
[latex]\vec{v}_{Q}=\vec{\Omega }\times \vec{r}_{Q-CIR}=\begin{vmatrix} i &j &k \\ 0& 0& \Omega \\ -0,173& 0,30& 0 \end{vmatrix}[/latex]
[latex]\vec{v}_{Q}=(-0,30)(57,7)\frac{m}{s}\breve{i}+(-0,173)(57,7)\frac{m}{s}\breve{j}[/latex]
[latex]\vec{v}_{Q}=-17,31\frac{m}{s}\breve{i}-9,98\frac{m}{s}\breve{j}[/latex]
2.- Una escalera homogénea de longitud L = 1 m, está apoyada en el piso y en la pared. Conociendo el ángulo de inclinación α = 30°, y la velocidad del punto A, [latex]\vec{v}_{A}=-2\frac{m}{s}\breve{j}[/latex], hallar, para esta posición:
a) La velocidad del CM
b) La velocidad del punto B
c) La posición del CIR
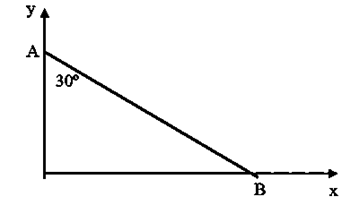
¿Son suficientes los datos para resolver el problema?
Conocemos la geometría del problema. Sabemos (o podemos suponer) que se trata de un cuerpo rígido (es decir que vamos a despreciar cualquier deformación que pudiera sufrir una escalera real en esas condiciones). Además tenemos el dato de la velocidad del punto A. Con esta información no resulta posible resolver el problema. Pero ¿es toda la que disponemos? El enunciado dice que la escalera está apoyada en el piso. Es decir que el punto B no está libre sino que tiene un vínculo (una restricción al desplazamiento). En este caso, el desplazamiento del punto B sólo puede tener componente en la dirección x, ya que dicho extremo de la escalera no se separa del piso. Por lo tanto [latex]\vec{v}_{B}=v_{B}\breve{i}[/latex] pero también [latex]{v}_{By}=0 \frac{m}{s}[/latex] (este es un dato más que debemos agregar a los anteriores.)
¿Estamos ahora en condiciones de resolver el problema? O, de manera más general, ¿con cuántos parámetros podemos obtener el campo de velocidades[6] de todos los puntos de un cuerpo rígido? Según la condición de rigidez, la velocidad de un punto genérico “p” puede escribirse como [latex]\vec{v}_{P}=\vec{v}_{p'}+\vec{\Omega} \times \vec{r}_{P-p'}[/latex]. Para el caso de un movimiento plano (como el de este problema) sabemos que (eligiendo adecuadamente el sistema de ejes) el vector [latex]\vec{v}_{p'}[/latex] tiene siempre una coordenada igual a cero y el vector [latex]\vec{\Omega}[/latex] dos coordenadas iguales a cero. Por lo tanto, los parámetros que permiten obtener la velocidad de cualquier punto en función de su posición son tres (dos coordenadas de y una de ).
La condición de rigidez puede ser expresada de varias maneras, pero la cantidad de parámetros necesaria para poder poner [latex]\vec{v}_{P}[/latex] en función de [latex]\vec{r}_{P}[/latex] no varía. De manera que con [latex]v_{Ax}[/latex], [latex]v_{Ay}[/latex] y [latex]v_{By}[/latex] ya quedan determinadas las velocidades de todos los puntos de la escalera.
Empecemos por plantear la condición de rigidez. Como los puntos p y p’ pueden ser cualesquiera, podemos escribir:
[latex]\vec{v}_{A}=\vec{v}_{CM}+\vec{\Omega } \times \vec{r}_{A-CM}[/latex]
[latex]\vec{v}_{B}=\vec{v}_{CM}+\vec{\Omega } \times \vec{r}_{B-CM}[/latex]
Recordamos que:
[latex]\vec{\Omega }\times \vec{r}=\begin{vmatrix} i &j &k \\ 0& 0& \Omega_{z} \\ r_{x}& r_{y}& 0 \end{vmatrix}=-\Omega_{z}r_{y}\breve{i}+\Omega_{z}r_{x}\breve{j}[/latex]
Las ecuaciones (1) y (2) pueden descomponerse en:
[latex]x)v_{Ax}=v_{CMx}-\Omega _{z}r_{A-CMy}[/latex]
[latex]y)v_{Ay}=v_{CMy}-\Omega _{z}r_{A-CMx}[/latex]
[latex]x)v_{Bx}=v_{CMx}-\Omega _{z}r_{B-CMy}[/latex]
[latex]y)v_{By}=v_{CMy}-\Omega _{z}r_{B-CMx}[/latex]
Quedando un sistema de 4 ecuaciones con 4 incógnitas ( vCMx, vCMy, vBx y Ωz ). De esta manera resolvemos los puntos a y b.
c) Para la posición del CIR, podemos plantear
[latex]\vec{v}_{CIR}=\vec{v}_{CM}+\vec{\Omega } \times \vec{r}_{CIR-CM}[/latex]
A partir de estas ecuaciones podemos despejar las coordenadas de la posición del CIR respecto del CM.
Respuestas:
[latex]\vec{v}_{CM}=1,73 \frac{m}{s}\breve{i}-1\frac{m}{s}\breve{j}[/latex]
[latex]\vec{v}_{B}=3,45 \frac{m}{s}\breve{i}[/latex]
[latex]\vec{\Omega }=4\frac{1}{s}\breve{k}[/latex]
[latex]\vec{r}_{CIR}=0,5m\breve{i}+0,87m\breve{j}[/latex]
SIMULACIÓN PROBLEMA ESCALERA
https://www.geogebra.org/m/SEF2VUSs
3.-El disco de la figura 18 gira con una velocidad angular ω = -3 s-1 mientras su centro O se desplaza con una velocidad [latex]\vec{v}=-5\, m/s \: \breve{j}[/latex]. Se dibuja la vista en planta, como si el disco se moviese sobre una mesa horizontal sin rozamiento. Si la barra AB tiene fijo su extremo B (un clavito que lo mantiene en posición respecto al LAB, pero que permite a la barra girar alrededor del clavito) y articulado (unido mediante un perno que permite rotaciones, que vinculan el punto “A” con un punto del disco) su extremo A, el punto “O” no está vinculado, hallar:
a) la velocidad del punto A de la barra
b) la velocidad angular de la barra AB
c) el CIR de la rueda
Datos: R = 1m y AB = 3m
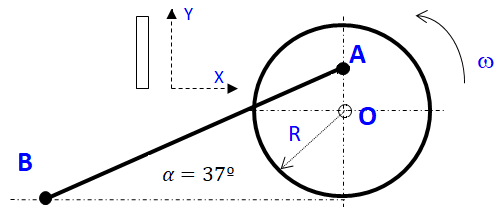
Antes de comenzar a plantear la solución del problema, analicemos cómo se mueven los cuerpos que componen el sistema. La barra AB está fija en B. El CIR de la barra es el punto B. Entonces, todos los puntos de la barra realizan un movimiento circular centrado en B. La velocidad de todos los puntos de la barra serán perpendiculares a la dirección de la misma y los módulos de sus velocidades serán [latex]\left | \vec{\Omega }_{AB} \right |\left | {\vec{r}}_{iB} \right |[/latex]. La rueda en cambio realiza un movimiento de rototraslación. De ese movimiento conocemos la velocidad angular Ω y la velocidad de su centro de masa O. Como la velocidad de O es horizontal, el CIR de la rueda estará ubicado en un eje vertical que pasa por O
[latex]\vec{v}_{A}=\vec{v}_{O}+\Omega \, d\, \breve{i}[/latex]
O sea,
[latex]\vec{v}_{A}=-5\, \frac{m}{s}\, \breve{j}+2,1\, \frac{m}{s}\, \breve{i}[/latex]
b) Como la barra AB realiza un movimiento circular con B quieto (su CIR) y R=3m, la velocidad de cada punto será ΩAB ri.
En el caso del extremo A:
[latex]{v}_{A}=\Omega _{AB}(3m)[/latex]
[latex]\Omega _{AB}=\frac{5,42}{3}s^{-1}[/latex]
[latex]\vec{\Omega} _{AB}=-1,8\, s^{-1}\breve{k}[/latex]
c) Para averiguar la posición del CIR de la rueda tenemos de dato las velocidades de los puntos o y A. Consideremos un sistema de coordenadas fijo en el CM. Como las velocidades de todos los puntos de la rueda serán de rotación pura respecto al CIR podemos escribir:
[latex]\vec{v} _{A}=\vec{\Omega }\times \vec{r}_{A-CIR}[/latex]
Por otro lado:
[latex]\vec{v} _{O}=\vec{\Omega }\times \vec{r}_{O-CIR}[/latex]
[latex]-5\, \frac{m}{s}\, \breve{j}=\begin{vmatrix} i & j & k\\ 0 & 0 & -3\\ -x_{CIR} & -y_{CIR} &0 \end{vmatrix}[/latex]
[latex]2,1\, \frac{m}{s}\, \breve{i}-5\, \frac{m}{s}\, \breve{j}=\begin{vmatrix} i & j & k\\ 0 & 0 & -3\\ x_{A}-x_{CIR} & y_{A}-y_{CIR} &0 \end{vmatrix}[/latex]
Operando e igualando término a término resulta:
xCIR = - 1, 67 m
yCIR = 0
xA = 0
yA = 0,7 m.
4.- El disco compuesto de la figura 19 gira y resbala sobre el piso horizontal. La velocidad lineal de la cuerda que sale de A es de 3,6 m/s hacia la derecha y el disco gira hacia la izquierda a 6 1/s. Calcule la velocidad de los puntos O (CM) y B. Datos: R = 0,9 m y r = 0,3 m.
Pensamos en base a los datos cómo se mueve el disco respecto al sistema laboratorio. Como la velocidad del punto A es hacia la derecha, la velocidad del punto de contacto con el piso será mayor que la de A hacia la derecha. Esto es porque la velocidad del CM que no conocemos es hacia la derecha y la velocidad de rotación alrededor del centro de masa en el punto de contacto es mayor a la de A (está más alejado y también es hacia la derecha). Como la velocidad de A y la del CM es horizontal, el CIR del disco se encuentra en algún punto de la vertical que pasa por el CM y por arriba del mismo.
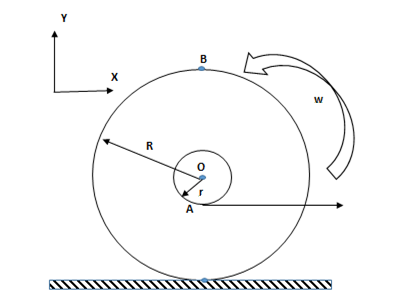
Elegimos un sistema de coordenado cartesiano ortogonal (x-y -z) ubicado en O.
Dado de dato la [latex]\vec{v}_{A}=3,6 \frac{m}{s}\, \breve{i}[/latex]. Sabemos que en A se suman vectorialmente la velocidad del CM y la de rotación.
[latex]\vec{v}_{A}=3,6 \frac{m}{s}\, \breve{i}=\vec{v}_{O}+6\, s^{-1}(0,3\, m)[/latex]
Encontramos así la velocidad del punto O.
[latex]\vec{v}_{O}=1,8\frac{m}{s}\, \breve{i}[/latex]
La velocidad de B será
[latex]\vec{v}_{B}=\vec{v}_{O}+\vec{\Omega }\times \vec{r}_{B}=1,8\, \frac{m}{s}\, \breve{i}-5,4\, \frac{m}{s}\, \breve{i}[/latex]
[latex]\vec{v}_{B}=-3,6\, \frac{m}{s}\, \breve{i}[/latex]
Si queremos encontrar el CIR de la rueda será:
[latex]\vec{v}_{CIR}=\vec{0}=\vec{v}_{O}+\vec{\Omega }\times \vec{r}_{CIR-O}[/latex]
[latex]\vec{0}=1,8\, \frac{m}{s}\, \breve{i}-6\, s^{-1}\, y_{CIR}\, \breve{j}[/latex]
CIR: (0; 0,3 m; 0)
Verifiquemos, por ejemplo, la velocidad del punto B con los datos encontrados.
[latex]\vec{v}_{B}=\vec{\Omega }\times \vec{r}_{B-CIR}[/latex]
[latex]\vec{v}_{B}=-6\, s^{-1}(0,9-0,3)m\, \breve{i}[/latex]
[latex]\vec{v}_{B}=-3,6\, \frac{m}{s}\, \breve{i}[/latex]
[1] La primera y la segunda ecuación universal para los sistemas de partículas con referencia a sistemas inerciales, que se ven en este curso, son aplicables a la mecánica de todos los sistemas de partículas clásicas, con la única excepción de fuerzas de interacción magnética en casos muy especiales que quedan fuera del alcance de este texto.
[2] Si consideramos lo ventajoso que es referir el estudio de la mecánica del Cuerpo Rígido al Centro de Masa (CM), deberíamos prestar mucha más atención a la velocidad y la aceleración del CM pues estas variables están íntimamente unidas a la cantidad de movimiento y a la resultante de las fuerzas exteriores aplicadas al cuerpo rígido, respectivamente.
La posición del CM, en ocasiones resulta estar en un punto que no tiene existencia material, pero que se considera conceptualmente como perteneciente al cuerpo rígido.
[3] La densidad constante se verifica para un medio continuo y para diferenciales de volúmenes pertenecientes a ese medio. Pero los volúmenes físicos no pueden ser extremadamente pequeños, pues queremos desarrollar aquí una mecánica clásica de los medios continuos sin introducirnos en la intimidad del estado sólido.
[4] Observemos que no es lo mismo que la aceleración tangencial.
[5] Si bien la fuerza de rozamiento es tema de discusión en dinámica del cuerpo rígido, hemos preferido incluirla en este ejemplo para completar la idea de su aplicación como modelo mecánico. No se pretende que se entienda este tema en una primera lectura, retome este punto cuando haya finalizado la lectura del capítulo de dinámica del cuerpo rígido.
[6] Interpretamos la expresión “campo de velocidades” asignando a cada punto del espacio un vector velocidad. Tal asignación debe ser coherente con la condición de rigidez.
