Índice

1. Introducción
2. Centro de percusión
3. Centro de percusión de cuerpos suspendidos
4. Aplicaciones de centro de percusión

Dinámica impulsiva del Cuerpo Rígido

1_ INTRODUCCIÓN

 Consideremos una situación en la que sobre un CR se aplica un impulso. Por ejemplo, se golpea una varilla en un brevísimo intervalo de tiempo aplicando una fuerza variable que puede tener instantáneamente un valor muy grande. Durante ese breve intervalo de tiempo el CR cambia su estado de movimiento pero sin cambiar de posición. Es como si estuviéramos mirando una película y detuviéramos el rodaje. Así es como modelizamos el intervalo de tiempo en estudio. En ese intervalo brevísimo de tiempo los cuerpos que chocan se deforman e incluso cambian a veces el sentido del movimiento, pero, sin cambiar su posición en el espacio. La parte de la física que estudia el proceso que ocurre en estos casos se denomina dinámica impulsiva.

Aquí advertiremos con claridad cómo el comportamiento de un CR difiere del de una partícula individual. Por ejemplo, veremos que la energía cinética que adquiere un CR como consecuencia de la aplicación de un impulso instantáneo depende del punto del rígido en el que se aplique dicho impulso, dependencia que no existe para una partícula.

Además de su interés intrínseco, como problema de Mecánica Clásica, la dinámica impulsiva anticipa algunos formalismos de Física Moderna, especialmente los de Mecánica Cuántica; por ejemplo, la forma de escribir la energía cinética en términos del impulso elevado al cuadrado. En general, distintas cuestiones de CR, tales como la dinámica impulsiva que estamos ahora comenzando a estudiar y otras como el Teorema de Noether trazan un “puente” entre la Física Clásica y la Física Cuántica.

En la Dinámica Impulsiva sólo se tienen en cuenta los impulsos exteriores al sistema en estudio producidos por fuerzas variables, porque los impulsos de fuerzas de módulo acotado (constantes o variables) son despreciables.

Definimos el impulso  como [latex]\vec{J}=\int \vec{F}dt[/latex] pero si el módulo de la fuerza es acotada y constante (para  simplificar el cálculo) se puede sacar fuera de la integral:

[latex]\vec{J}=\int \vec{F}dt=\vec{F}\int dt[/latex]

[latex]\therefore \: \: \vec{J}=\vec{F}\, \Delta t[/latex]

como Δt→0 el impulso es despreciable.

¿Qué ecuaciones podemos aplicar durante la acción de impulsos exteriores?

La 1° Ecuación de la dinámica del CR es:

[latex]\sum \vec{F}=M\, \vec{a}_{CM}[/latex].

Si integramos en el tiempo resulta:

[latex]\sum \vec{J}=\Delta \, \vec{P}_{CM}[/latex]

La 2° Ecuación de la dinámica del CR es:

[latex]\sum \vec{M}_{CM}=\frac{d\vec{L}^{CM}}{dt}[/latex]

Si la integramos en el tiempo resulta:

[latex]\int \vec{M}_{Fneta}^{CM}\, dt=\int d\vec{L}^{CM}[/latex]

Esta última ecuación se puede escribir como [latex]\vec{r}_{CM}\times \vec{J}_{neto}=\Delta \vec{L}^{CM}[/latex]

Ecuaciones fundamentales de la Dinámica Impulsiva:

1° Ecuación         

 [latex]\sum \vec{J}_{ext}=\Delta \, \vec{P}_{CM}[/latex]

2° Ecuación         

[latex]\vec{r}_{CM}\times \vec{J}_{neto}=\Delta \vec{L}^{CM}[/latex]

Si se analizan las ecuaciones anteriores para un cuerpo libre, se observa que la variación de la cantidad de movimiento lineal es la misma si el impulso se aplica en el CM o si se aplica por arriba o por debajo del CM.  Pero, la variación del momento cinético aumenta si el impulso se aplica cada vez más lejos del CM. De esto se puede decir que el cambio que se produce en la traslación no depende de dónde se aplique el impulso, pero, el cambio en la velocidad de rotación depende de la distancia con respecto al CM en donde se aplica el impulso.

2_ CENTRO DE PERCUSIÓN

De lo anteriormente expuesto se llega a la conclusión que si se tiene un CR apoyado sobre una superficie horizontal con rozamiento y se lo golpea con un impulso J a una altura h del CM, el CR puede rodar sin deslizar una vez que el mismo deje de actuar.

¿Cuál es la altura?

¿Cuál es la altura?

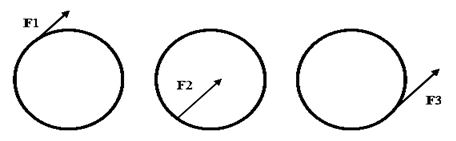
Si se reemplaza v_CM = Ω R (donde R es el radio del CR) y considerando  I^CM = M k² (donde k es el radio de giro baricéntrico del CR)

h J = M k² Ω

h M Ω R = M k² Ω

Si se simplifica esta expresión:

[latex]h=\frac{k^{2}}{R}[/latex]

La distancia al punto de contacto (CIR) a la que debe aplicarse el impulso es entonces

[latex]h=\frac{k^{2}}{R}+R[/latex]

La altura a la cual debe darse el impulso de modo que el punto de contacto sea un CIR se denomina Centro de Percusión correspondiente a ese punto.

El centro de percusión correspondiente a un punto A del CR, es otro punto que puede estar en el CR o fuera de él, para el cual al aplicar un impulso el CR tiene su CIR en el punto A.

3_CENTRO DE PERCUSIÓN DE CUERPOS SUSPENDIDOS

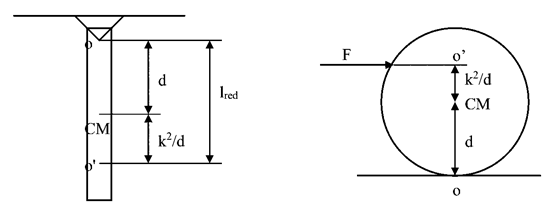
Si se suspende un CR desde un punto O ubicado una distancia d por encima de su centro de gravedad (que coincida con el CM), habrá una distancia respecto a su CM que se denomina [latex]h=\frac{k^{2}}{d}[/latex] (A) tal que si se aplica un impulso en A el cuerpo tiene naturalmente su CIR en el punto O. La distancia total entre O y A se llama l (longitud reducida, ver péndulo físico). Este punto A es el centro de percusión del punto O. De igual forma, cada punto del cuerpo tiene su propio centro de percusión ubicado a una distancia igual a la longitud reducida del centro de suspensión O (ver figura 2).

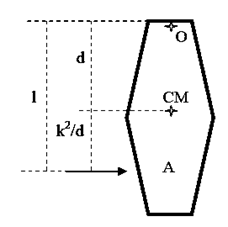
Esto quiere decir que no siempre el CIR natural para un cuerpo suspendido coincide con el punto de suspensión O. Sólo en el caso que se golpee al cuerpo a una distancia igual a la longitud reducida O coincide con el CIR. En otras palabras, sólo en ese caso, no existe impulso reactivo horizontal en O.

Volviendo al caso de un cuerpo apoyado sobre una mesa sin rozamiento, si se le aplica inicialmente un impulso en el centro de percusión el cuerpo rota naturalmente alrededor del punto O. El punto O es el CIR natural para el centro de percusión.

Vemos entonces que para cada punto de suspensión O  cambia d y por lo tanto cambia la distancia al centro de percusión. Existe un centro de percusión para cada punto de suspensión, pero, su distancia está siempre a k2/d  + d. Esta expresión coincide con la longitud reducida. Es decir, la distancia entre el centro de suspensión y el centro de percusión es igual a la longitud del péndulo ideal sincrónico con el péndulo físico.

En los deportes, las raquetas y paletas se refuerzan en el centro de percusión correspondiente al lugar en que colocamos la mano. También los bates de béisbol se refuerzan internamente con acero en la zona de percusión. Algo similar ocurre con n las herramientas. En estos casos el centro de percusión es el lugar del impacto y el CIR el punto desde donde se sostienen.

Problema : Veamos  que sucede si se le da un impulso a una barra delgada apoyada sobre una mesa horizontal con rozamiento despreciable (la barra no está sujeta a la mesa).  Podemos analizar tres casos: 1º si la recta de acción del impulso pasa por el CM. 2º si la recta de acción del impulso pasa por uno de los extremos de la barra y 3º si la recta de acción del impulso pasa por un punto intermedio entre el CM y el extremo de la barra. ¿Si el módulo de J permanece constante qué magnitudes cambian y cuáles no?   ¿El movimiento resultante de la barra será el mismo?

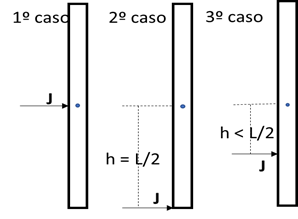
Encontremos en cada caso la  [latex]\vec{v}_{CM}[/latex]; el [latex]\vec{\Omega}[/latex]; la cantidad de movimiento angular [latex]\vec{L}[/latex] y la E_C de la barra después de aplicado el impulso.

Las ecuaciones fundamentales de la dinámica impulsiva de un CR son:

 [latex]\sum \vec{J}_{ext}=\Delta \, \vec{P}_{CM}[/latex]

[latex]\vec{r}_{CM}\times \vec{J}_{neto}=\Delta \vec{L}^{CM}[/latex]

Aplicaremos estas ecuaciones a cada caso representado en la figura con el sistema de referencia colocado en el CM y un sistema de coordenadas cartesiano ortogonal.

1ºcaso

[latex]\vec{J}=M\, v_{CM}\: \breve{i}[/latex]

[latex]\vec{L}=\vec{0}[/latex]

[latex]\vec{\Omega }=\vec{0}[/latex]

2ºcaso

[latex]\vec{J}=M\, v_{CM}\: \breve{i}[/latex]

[latex]J\, h\, \breve{k}=I_{CM}\, \Omega\: \breve{k}[/latex]

3ºcaso

[latex]\vec{J}=M\, v_{CM}\: \breve{i}[/latex]

[latex]J\, \frac{L}{2}\, \breve{k}=I_{CM}\, \Omega\: \breve{k}[/latex]

[latex]\vec{v}_{CM}=\frac{\vec{J}}{M}[/latex]

[latex]\vec{\Omega }=\frac{\vec{J}h}{I_{CM}}[/latex]

[latex]\vec{\Omega }=\frac{12\vec{J}h}{ML^{2}}[/latex]

Al comparar los resultados obtenidos vemos que la v_CM   siempre que J sea constante es la misma independientemente de dónde se aplique el impulso; en cambio L  y Ω aumentan a medida que J se aleja del CM.

¿Qué pasa con la E_C?

[latex]E_{c}=\frac{1}{2}Mv_{CM}^{2}+\frac{1}{2}I_{CM}\Omega ^{2}[/latex]

La energía cinética de traslación es la misma para los tres casos y la energía cinética de rotación aumenta de cero a un valor máximo en el segundo caso.

Aquí aparece la diferencia que indicábamos en la introducción. Al recibir un impulso instantáneo el rígido se comporta de una forma muy diferente que una partícula.

Encontremos la expresión de la energía cinética para un caso genérico.

[latex]E_{c}=\frac{J^{2}}{2M}+\frac{6J^{2}h^{2}}{ML^{2}}[/latex]

Vemos que la energía cinética de rotación aumenta al aumentar h.

Ej.: Encontrar la energía cinética total del CR para los tres casos estudiados.

¿Cuál es su valor máximo?

Es para h = L/2 donde E_{c max}= 2 J²/M

4_APLICACIONES DE CENTRO DE PERCUSIÓN

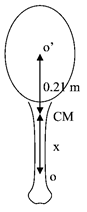
Problema 1:

Una raqueta de tenis cuyo centro de masa se encuentra a 0,21m del centro del encordado, oscila suspendida de ese centro con T=1,36 s. Un tenista desea utilizarla para impactar la pelotita justo en ese centro “o”. Calcular de qué punto “o” debe tomar la raqueta, para no experimentar reacción (lineal) en la mano.

Conceptos teóricos previos

a) Longitud reducida: distancia del centro de suspensión al centro de percusión (que es el punto en el cual puede aplicarse una fuerza sin que aparezca una reacción en el vínculo).

b) Radio de giro baricéntrico “k”. Se puede interpretar físicamente como el radio de un aro de masa igual a la del cuerpo rígido en cuestión y que tiene igual momento de inercia baricéntrico.

c) Analogía cuerpo suspendido y apoyado para el cálculo de la longitud reducida.

Resolvemos el problema planteado con estos conceptos y usando los datos

[latex]T=2\pi \sqrt{\frac{l_{red}}{g}}[/latex]

con [latex]l_{red}=\frac{k^{2}}{d}+d[/latex]

Entonces:

[latex]T=2\pi \sqrt{\frac{l_{red}}{g}}[/latex]    →    [latex]l_{red}=\left (\frac{Tg}{2\pi } \right )^{2}[/latex]

[latex]l_{red}=\frac{(1,36s)^{2}(9,8 \, m/s^{2})^{2}}{4\pi^{2} }=0,46\, m[/latex]

Como la l_red que corresponde a un centro de suspensión ubicado a una distancia d del CM es igual a la que corresponde a otro centro de suspensión ubicado a una distancia k²/d del CM (o sea a una distancia l_red del centro anterior), podemos pensar que si hacemos oscilar la raqueta tomándola del mango, a una distancia l_red del centro del encordado, el período será el mismo (y por lo tanto la longitud reducida también). En estas condiciones podemos aplicar la analogía anterior entre una raqueta que oscila suspendida de este nuevo punto y una raqueta golpeada en el centro del encordado que no experimenta reacción (lineal) en el vínculo.

Por lo tanto debe tomarse a 46 cm del centro del encordado (esto es, a 25 cm del centro de masa: X= 25 cm)

Problema 2:

¿A qué distancia y F del centro de una bola de billar de radio R debe aplicarse un tacazo para que comience a desplazarse sin reacción de vínculo en el punto de apoyo sobre el paño?

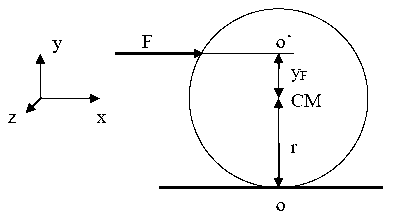
Primero dibujamos el D.C.L. de la bola en el momento de recibir el golpe

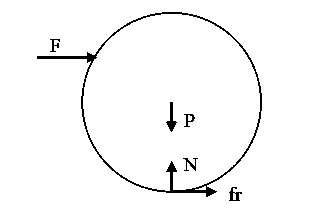
Planteamos las ecuaciones dinámicas para el cuerpo rígido en cuestión:

 [latex]\sum \vec{F}=m\, \vec{a}_{CM}[/latex]

[latex]\sum \vec{M}^{CM}=I^{G}\, \vec{\gamma }[/latex]

Descomponiendo la primera ecuación vectorial en sus componentes (y quedándonos sólo con la que nos interesa, que es aquella cuya dirección coincide con la de la posible aceleración del CM).

[latex]x)\: \sum {F}_{x}=m\, \, a_{CMx}\: \rightarrow \: F+f_{r}=m\, a_{CMx}[/latex]

[latex]z)\: \sum {M_{z}^{CM}}=I^{G}\, \, \gamma _{z}\: \rightarrow \: -F\, y_{F}+f_{r}\, R=-I^{G}\, \, \gamma[/latex]

Hasta acá tenemos dos ecuaciones y tres incógnitas, pero debido a la condición de rodar sin deslizar, existe una relación entre la aceleración del CM (en este caso consideraremos la componente horizontal) y la aceleración angular:

[latex]x)\: a_{CMx}=\gamma \, R[/latex]

La relación de módulos anterior proviene de analizar la situación vectorial expresada por la siguiente ecuación (ver teoría correspondiente).

[latex]\vec{a}_{CIR}=\vec{a}_{CM}+\vec{\gamma }\times \vec{r}_{CM-CIR}+\vec{\Omega }\times (\vec{\Omega }\times\vec{r}_{CM-CIR} )[/latex]

Se puede demostrar por consideraciones cinemáticas que, para un cuerpo en esas condiciones, la aceleración del CIR en la dirección paralela al plano sobre el cual está rodando (en este caso a_{CIR x}) es igual a cero.

Ahora tenemos un sistema de tres ecuaciones con tres incógnitas a_CM, γ y f_r

Resolviéndolo llegamos a:

[latex]f_{r}=m\, a_{CM}\frac{y_{F}-\frac{2}{5}R}{R+y_{F}}[/latex]

Entonces:

[latex]f_{r}=0\: \rightarrow \: y_{F0}=\frac{2}{5}R[/latex]

El punto en donde se debe aplicar una fuerza para que no aparezca una reacción en el vínculo se llama centro de percusión, y su distancia al centro de masa también se puede calcular como y_F0 = k²/R, donde k es el radio de giro baricéntrico.

[latex]I^{G}=mk^{2}\: \rightarrow \: \frac{k^{2}}{R}=\frac{I^{G}}{mR}=\frac{\frac{2}{5}mR^{2}}{mR}=\frac{2}{5}R\: \rightarrow \: y_{F0}=\frac{2}{5}R[/latex]

Si en lugar de aplicarse la fuerza en el centro de percusión, se aplica por encima o por debajo de ese punto, la fuerza de rozamiento ya no es cero.

[latex]Si \:\: \: y_{F}> y_{F0}\: \rightarrow \: f_{r}> 0[/latex]

[latex]Si \:\: \: y_{F}< y_{F0}\: \rightarrow \: f_{r}< 0[/latex]

Problema 3:

¿A qué distancia del CM se debe golpear con un martillo cuya cabeza es un paralelepípedo (de lados a=5cm, b=10cm y c=5cm) de 2 Kg de masa y su mango una varilla de 30 cm de longitud y masa despreciable?

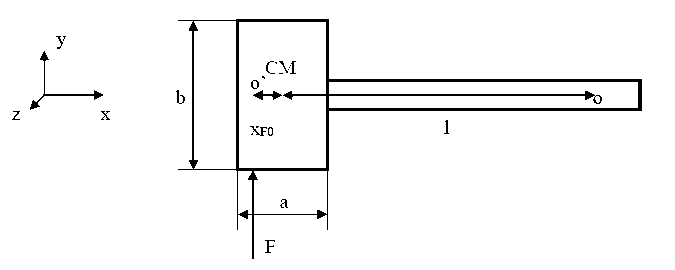
Según lo visto en el problema anterior, se debe golpear en el centro de percusión. Su distancia x_F0 al centro de masa se calcula como:

[latex]x_{F0}=\frac{I^{G}}{ml}=\frac{m\, \frac{a^{2}+b^{2}}{12}}{ml}=\frac{a^{2}+b^{2}}{12l}=\frac{(5cm)^{2}+(10cm)^{2}}{12\, (30cm)}=0,35 \, cm[/latex]

Problema 4:

Se le da un tacazo a una bola de billar por encima de su CM. Como resultado del mismo la bola adquiere una velocidad [latex]\vec{v}_{0}[/latex] en su centro de masa y desliza respecto de la mesa de pool (o de billar). Luego de un cierto tiempo comienza a rodar sin deslizar siendo en este caso la velocidad del CM [latex]0,7\, \vec{v}_{0}[/latex]. Encuentre la altura h a la que se le dio el tacazo.

El enunciado indica que la bola de billar recibe un impulso J a una altura h de su centro de masa y no conocemos el valor del impulso ni de su altura que es la incógnita que se nos pide calcular. Como el impulso no pasa por el CM una vez aplicado el mismo, la bola de billar ha adquirido también una rotación w₀ que se desconoce. El único dato es la velocidad del CM cuando el impulso deja de actuar y la velocidad del CM cuando comienza a rodar sin deslizar. Este último dato nos dice que la velocidad del CM durante el tramo del deslizamiento disminuye. Esto indica que cuando deja de actuar el impulso la bola desliza hacia adelante y la fuerza de rozamiento dinámica disminuye su módulo oponiéndose al deslizamiento relativo (es hacia atrás). En la figura se muestra el único impulso exterior que actúa durante el tacazo, los efectos producidos sobre la bola, el estado de movimiento de la bola cuando deja de actuar el impulso y el DCL durante el deslizamiento con la mesa de billar.

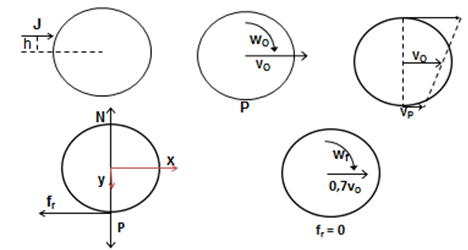
Durante el impulso escribimos las ecuaciones fundamentales de la dinámica impulsiva:

 [latex]\sum \vec{J}_{ext}=\Delta \, \vec{P}_{CM}[/latex]

[latex]\vec{r}_{CM}\times \vec{J}_{neto}=\Delta \vec{L}^{CM}[/latex]

En nuestro caso y aplicando el sistema de referencia indicado en la cuarta figura

[latex]x) \: J=M\, v_{0}[/latex]

[latex]z) \: Jh=\frac{2}{5}MR^{2}\, \omega _{0}[/latex]

Reemplazando J en la segunda ecuación y simplificando:

[latex]h=\frac{\frac{2}{5}MR^{2}\, \omega _{0}}{v_{0}}[/latex]

La velocidad es conocida pero la velocidad angular es desconocida y la debemos calcular.

En el intervalo desde un instante posterior al del impulso y hasta que comienza a rodar sin deslizar, aplicamos las ecuaciones fundamentales de la dinámica del CR  (traslación y rotación)

[latex]\sum \vec{F}=Ma_{CM}[/latex]

[latex]\sum \vec{r}\times \vec{F}=\frac{d\vec{L}}{dt}[/latex]

De acuerdo con nuestro sistema de coordenadas ubicado en el CM

[latex]x)\: -f_{r}=M\, a_{CM}[/latex]

[latex]y)\: P-N=0[/latex]

[latex]z)\: f_{r}R=\frac{2}{5}MR^{2}\,\gamma[/latex]

de la segunda ecuación como la fuerza de rozamiento es dinámica, es constante y su valor [latex]f_{r}=\mu Mg[/latex]. De lo dicho sacamos la conclusión que la aceleración del centro de masa es constante. Entonces la aceleración media coincide con la instantánea. Podemos escribir:

[latex]-\mu Mg=M\frac{\Delta v}{\Delta t}[/latex]

y por las mismas consideraciones

[latex]\mu MgR=\frac{2}{5}MR^{2}\frac{\Delta \omega }{\Delta t}[/latex]

Si dividimos miembro a miembro y simplificamos

[latex]-R=\frac{2}{5}R^{2}\frac{\Delta \omega }{\Delta v}[/latex]

o sea

[latex]v_{0}-0,7v_{0}=\frac{2}{5}R(\omega _{0}-\omega _{f})[/latex]

como en el instante final la bola rueda sin deslizar   [latex]\omega _{f}R=0,7v_{0}[/latex]

Si reemplazamos ω₀ por [latex]\frac{\frac{5}{2}\, h\, v_{0}}{R^{2}}[/latex] nuestro cálculo resulta

[latex]0,3\, v_{0}\, R=h\, v_{0}-\frac{2}{5}\, 0,7\, v_{0}\, h[/latex]

Simplificando

[latex]0,3\, R=\left ( 1-\frac{7}{25} \right )h[/latex]

[latex]h=\frac{15}{36}R[/latex]