Índice
- Introducción
- Resultado de trasladar una fuerza al CM
- Cupla o par de fuerzas
- Resultante de un sistema de fuerzas aplicado a un CR
- Momento cinético de un CR en rotación pura
- Cálculo del momento de inercia baricéntrico de un cilindro respecto de un eje perpendicular a su eje de simetría
- Cálculo del momento de inercia de una chapa rectangular
- Teorema del Steiner o de los ejes paralelos
- Cálculo del momento cinético respecto a un eje cualquiera
- Momento cinético relativo al CIR
- Los momentos de inercia son aditivos y sustractivos
- Momentos de inercia baricéntricos de cuerpos no homogéneos y/o no simétricos
- Péndulo físico
- Energía en el CR
- Trabajo y energía para el CR
- Ecuaciones fundamentales de la dinámica del CR
- Acerca de la fuerza de rozamiento
- Aplicaciones de dinámica del CR
- Situación problemática especial de integración metodológica
Dinámica del Cuerpo Rígido (CR)
1_ INTRODUCCIÓN
Corresponde ahora que analicemos las diferencias entre los efectos producidos en el movimiento de un objeto cuando se le aplica un sistema de fuerzas, si se toma como modelo del mismo un punto material o se lo considera un cuerpo rígido (CR).
Si aplicamos un sistema espacial de fuerzas sobre una partícula, dicho sistema será necesariamente un sistema de fuerzas concurrentes, cuya resultante producirá la aceleración de la partícula. Si el modelo a aplicar es el de cuerpo rígido, las fuerzas no necesariamente son concurrentes (en particular no siempre están aplicadas en el centro de masa).
¿Qué consecuencias trae esto? El efecto producido por fuerzas exteriores aplicadas al cuerpo es diferente si se aplican en diferentes puntos de éste. Por ejemplo, si sobre un mismo cuerpo actúa una fuerza de igual módulo, dirección y sentido pero aplicada en diferentes puntos como se muestra en la figura 1, es lógico pensar que no se moverá de la misma forma.
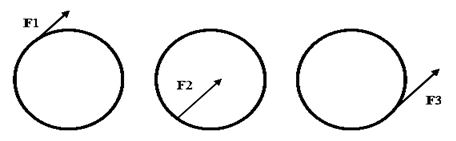
Por otro lado, si se analiza cómo trasladar una fuerza, luego es posible operar de la misma forma con todas las demás.
2_ RESULTADO DE TRASLADAR UNA FUERZA AL CM
Para que el efecto producido por la fuerza F no cambie, se agrega al sistema un par idénticamente nulo de igual intensidad o norma y de una dirección paralela a F que pasa por el CM.
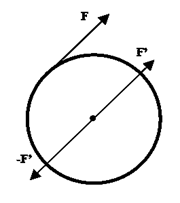
F’ es la fuerza F trasladada al CM y F junto con -F’ forman lo que se denomina cupla o par de fuerzas.
Trasladar, entonces, una fuerza al CM da por resultado la fuerza aplicada en otro punto (en este caso el CM) más una cupla.
Se debe analizar la novedad que se ha producido, por ello se estudia a continuación la cupla.
3_ CUPLA O PAR DE FUERZAS
Una cupla es un par de fuerzas, de igual intensidad y sentidos opuestos, en rectas de acción paralelas separadas una distancia “d”.
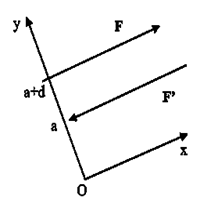
La resultante (su suma) es cero. [latex]\vec{F}+\vec{F'}=\vec{0}[/latex]
El momento o torque resultante de la cupla es:
[latex]\vec{M}_{CUPLA}^{0}=\vec{M}_{F}^{0}+\vec{M}_{F'}^{0}[/latex]
Para ello se considera como centro de momentos un punto O cualquiera del plano de la cupla. Se elige un sistema de coordenadas adecuado, de manera de simplificar el cálculo de los momentos. Como las fuerzas son axiales, se pueden deslizar a lo largo de sus rectas de acción.
Por esta razón, se va a considerar que [latex]\vec{r}_{F}=(0;a;0)[/latex] y [latex]\vec{r}_{F'}=(0;a+d;0)[/latex] donde “d” es la distancia entre las fuerzas de la cupla.
[latex]\vec{M}_{CUPLA}^{0}=(0;a;0)\times (F;0;0)+(0;a+d;0)\times (-F;0;0)[/latex]
Operando los productos vectoriales
[latex]\vec{M}_{CUPLA}^{0}=Fa\, \breve{k}-F(a+d)\, \breve{k}[/latex]
Si se aplica la propiedad distributiva y se simplifica:
[latex]\vec{M}_{CUPLA}^{0}=-Fd\, \breve{k}[/latex]
De acuerdo al resultado obtenido se puede afirmar que:
- El momento de la cupla es distinto de cero ya que tanto F como “d” son necesariamente no nulos.
- El momento de la cupla es el mismo para cualquier punto de su plano (es un invariante).
- Todas la cuplas del mismo plano dan momentos colineales (se pueden sumar algebraicamente).
Las cuplas tienen entonces la característica de tener [latex]\vec{R}=\vec{0}[/latex] (resultante nula) y [latex]\vec{M}_{0}\neq \vec{0}[/latex] (torque no nulo). Observamos que el efecto que produce una cupla es la variación en la velocidad de rotación del cuerpo alrededor del CM.
- ¿Conoce algunos ejemplos de cuplas que se apliquen en la vida diaria?
- ¿Por qué es más fácil abrir una canilla utilizando dos dedos que utilizando uno solo?
- Si la sumatoria de fuerzas sobre un cuerpo rígido es cero, ¿dicho cuerpo necesariamente permanecerá en reposo? Comparar el comportamiento de un cuerpo rígido con el de una partícula.
4_ RESULTANTE DE UN SISTEMA DE FUERZAS APLICADO A UN CR
Dijimos que si cada fuerza del sistema se traslada al CM se obtiene una fuerza más una cupla. La sumatoria de todas las fuerzas dará por resultado una fuerza neta aplicada al centro de masa y la sumatoria de todas las cuplas dará por resultado una cupla resultante. La fuerza neta producirá aceleración del CM (traslación) y la cupla una rotación alrededor del CM (rotación pura).
El Segundo Principio de la Dinámica, aplicado al CR, es idéntico al de Sistema de Partículas:
[latex]\sum \vec{F}_{ext}=M\, \vec{a}_{CM}[/latex]
y constituye la Ecuación Fundamental de la traslación del CR. Tomando las componentes de estos vectores en los tres ejes de un sistema de coordenadas cartesianas ortogonales:
[latex]\sum \vec{F}_{X}=M\, \vec{a}_{CMx}[/latex]
[latex]\sum \vec{F}_{Y}=M\, \vec{a}_{CMy}[/latex]
[latex]\sum \vec{F}_{Z}=M\, \vec{a}_{CMz}[/latex]
¿Y las cuplas?
Falta agregar una ecuación de rotaciones. Para ello hay que hablar de otra magnitud vectorial: el momento cinético aplicado a un CR.
5_ MOMENTO CINÉTICO DE UN CR EN ROTACIÓN PURA
Supongamos un cuerpo de revolución, de forma cualquiera, gira alrededor de un eje de simetría con velocidad angular [latex]\vec{\Omega }[/latex] unica y normal al plano que se analiza, como indicamos en la figura siguiente:
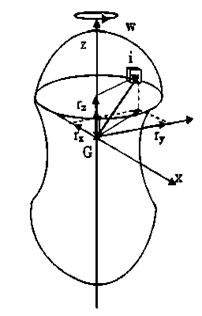
Para hallar el momento cinético o momento angular [latex]\vec{L}[/latex] , respecto al centro de masa (CM), se divide previamente el cuerpo en infinitos elementos de volumen (dvol = dx dy dz) o cubos elementales. Cada uno de ellos realizará un movimiento circular en el plano horizontal (perpendicular al eje de rotación). Como ejemplo se ha dibujado un elemento geométrico “i” que se mueve en un plano que se encuentra a una altura rz por encima de CM. Su velocidad es:
[latex]\vec{v}_{i}=\vec{\Omega }\times \vec{r}=\begin{vmatrix} i & j & k\\ 0 & 0 & \Omega \\ r_{x} & r_{y} & r_{z} \end{vmatrix}=-r_{y}\vec{\Omega }\, \breve{i}+r_{x}\vec{\Omega }\, \breve{j}[/latex]
El momento cinético del elemento de diferencial de volumen i es
[latex]d\vec{L}_{i}^{G}=\vec{r}_{i-G}\times \vec{p}_{i}=dm(\vec{r}_{i-G}\times \vec{v}_{i})=\begin{vmatrix} i & j & k\\ r_{x} & r_{y} & r_{z} \\ -r_{y}\Omega \, dm & r_{x}\Omega \, dm & 0 \end{vmatrix}[/latex]
[latex]d\vec{L}_{i}^{G}=-r_{x}\, r_{z}\Omega \, dm\, \breve{i}-r_{y}\, r_{z}\Omega \, dm\, \breve{j}+(r_{x}^{2}+r_{y}^{2})\Omega \, dm\, \breve{k}[/latex]
Si se quiere encontrar el momento cinético de todo el CR respecto al centro de masa, se tendrá que integrar la expresión anterior en todo el volumen del cuerpo.
[latex]d\vec{L}^{G}=\int d\vec{L}_{i}^{G}=-\Omega \int r_{x}r_{z}dm\breve{i}-\Omega \int r_{y}r_{z}dm\breve{j}+\Omega \int (r_{x}^{2}+r_{y}^{2})dm\breve{k}[/latex]
Observar que las integrales tienen la forma de [latex]\int d^{2}dm[/latex]. Se denominan momentos de segundo orden (donde “d” es una coordenada de posición respecto del punto de referencia considerado).
Lo precedente nos introduce en la importante noción del momento de inercia. Es frecuente definir este concepto como el análogo rotacional de la masa; sin embargo, si bien existen entre ambas determinadas analogías, también podemos advertir profundas diferencias.
Empecemos por las similitudes. Sabemos que la masa es una medida de la inercia, es decir, de la resistencia que la materia presenta al cambio de movimiento, a adquirir una aceleración. El momento de inercia, por su parte, puede pensarse como una inercia de rotación, como la resistencia que un cuerpo presenta a modificar su estado rotacional; es decir, a adquirir una aceleración angular.
Sin embargo, el momento de inercia es matemáticamente muy diferente de la masa. Para comprenderlo más claramente, vamos primero a definirlo y luego a efectuar algunos cálculos.
Definimos entonces el momento de inercia con respecto al centro de masa de un cuerpo rígido de la siguiente forma: [latex]I_{CM}=\int r^{2}dm[/latex]
Como veremos a continuación, el momento de inercia dependerá del eje respecto del cual efectuaremos el cálculo.
6_ CÁLCULO DEL MOMENTO DE INERCIA BARICÉNTRICO DE UN CILINDRO RESPECTO DE UN EJE PERPENDICULAR A SU EJE DE SIMETRÍA
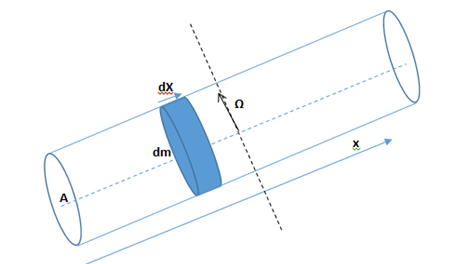
Encontremos el momento de inercia del cilindro, respecto a un eje baricéntrico perpendicular a su eje de simetría (eje del cilindro), tomando como elemento de masa un disco de área A y espesor dx cuyo volumen será A.dx y su masa dm.
El momento de inercia baricéntrico del cilindro lo definimos como [latex]I_{CM}=\int r^{2}dm[/latex]. Como la integral entre –L/2 y +L/2 se anula, el resultado lo encontramos multiplicando por 2 el cálculo de la integral entre x = 0 y x = L/2. El elemento de masa dm lo vamos a reemplazar por el producto de la densidad por el volumen elemental propuesto [latex]dm=\rho\, A\, dx[/latex] y la variable r en nuestro caso será la variable x.
La integral resulta ser:
[latex]I_{CM}=2\int_{0}^{L/2}x^{2}\rho\, A\, dx[/latex]
Como la densidad y la sección son constantes salen fuera de la integral
[latex]I_{CM}=2\, \rho\, A\int_{0}^{L/2}x^{2} dx[/latex]
[latex]I_{CM}=2\, \rho\, A \left ( \left.\begin{matrix} \frac{x^{3}}{3} \end{matrix}\right|_{0}^{L/2} \right )[/latex]
Con x variando entre 0 y L/2
[latex]I_{CM}=2 \left ( \frac{M}{AL} \right ) A\left ( \frac{(L/2)^{3}}{3} \right )[/latex]
el resultado es
[latex]I_{CM}= \frac{1}{12}ML^{2}[/latex]
Como por un punto pasan infinitas rectas, los cuerpos tienen múltiples momentos de inercia baricéntricos, uno respecto de cada eje que pasa por el CM.
Tomemos un ejemplo sencillo, el de dos masas iguales de masa m que podemos considerar puntuales, unidas a una barra de masa despreciable y de longitud L.
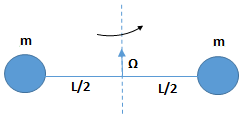
Si calculamos el momento de inercia baricéntrico respecto de un eje perpendicular a la barra, el resultado será la suma de los momentos de inercia de cada masa respecto del eje. Como cada masa es m y r = L/2
[latex]I_{CM}= 2m (L/2)^{2}[/latex]
[latex]I_{CM}= \frac{m L^{2}}{2}[/latex]
Este es el momento de inercia que debemos considerar si el sistema gira con respecto al eje vertical que pasa por el CM.
Veamos qué pasa si queremos hallar el momento de inercia baricéntrico respecto de un eje inclinado un ángulo α respecto a la barra.
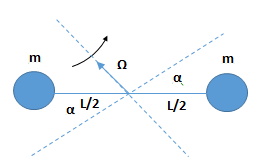
En este caso el r o sea la distancia al centro de masa a la que girarían las partículas es [latex]\frac{L}{2}sen \alpha[/latex]
Entonces el momento de inercia baricéntrico respecto al nuevo eje punteado es:
[latex]I_{CM}= 2m (\frac{L}{2}sen \alpha)^{2}[/latex]
[latex]I_{CM}=\frac{1}{2}m\, sen ^{2}\alpha \, L^{2}[/latex]
A partir del ejemplo precedente: ¿podríamos decir que el momento de inercia es una magnitud escalar?
7_ CÁLCULO DEL MOMENTO DE INERCIA DE UNA CHAPA RECTANGULAR
Vamos a calcular ahora el momento de inercia de una chapa rectangular de base b, altura h respecto de uno de los ejes de simetría.
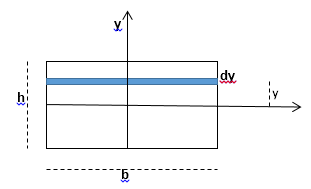
Calcularemos el momento de inercia respecto del eje x, para ello elegimos un elemento de superficie: bdy, donde b es la base y dy un elemento de altura.
[latex]I_{xx}=\int r^{2}dm[/latex]
El [latex]dm=\sigma ds[/latex]
Donde [latex]\sigma[/latex] es la densidad superficial de masa. Por convención se elige [latex]\sigma=1[/latex] y adimensional. Con lo cual podemos escribir:
[latex]I_{xx}=\int r^{2}ds[/latex]
La integral es una integral definida pero como entre – h/2 y +h/2 se anula, calculamos el doble de la integral entre 0 y h/2.
[latex]I_{xx}=2\, b\int_{0}^{h/2}y^{2}dy[/latex]
[latex]I_{xx}=\frac{bh^{3}}{12}[/latex]
Si queremos encontrar el momento de inercia de la chapa respecto del eje “y” operando de modo análogo resulta:
[latex]I_{yy}=\frac{hb^{3}}{12}[/latex]
Si deseamos el momento de inercia de la chapa respecto del eje z su resultado es la suma de los momentos de inercia respecto del eje “x” y respecto del eje “y”.
[latex]I_{zz}=I_{xx}+I_{yy}\[/latex]
[latex]I_{zz}=bh\frac{(b^{2}+h^{2})}{12}[/latex]
¿En qué unidades está usando el I? ¿Cómo puede interpretarlo cuando se aplica en superficies? ¿Tiene alguna relación con las condiciones adoptadas para [latex]\sigma[/latex]?
Ejemplificamos concluyendo que el momento de inercia no es un escalar, sino otra clase de entidad matemática, denominada tensor. En este caso el tensor es una matriz de 3x3, y consta entonces de nueve elementos. Por lo tanto, además de las halladas, se deben calcular otras seis componentes, los llamados momentos centrífugos [latex]I_{xy}[/latex];[latex]I_{yx}[/latex];[latex]I_{xz}[/latex];[latex]I_{zx}[/latex];[latex]I_{yz}[/latex] e [latex]I_{zy}[/latex] en los cuales se toman las distancias a uno y otro eje indicado en el subíndice.
La expresión del tensor de inercia resulta ser:
[latex]I=\begin{vmatrix} I_{xx} & I_{xy} & I_{xz}\\ I_{yx}& I_{yy} & I_{yz}\\ I_{zx}& I_{zy} & I_{zz} \end{vmatrix}[/latex]

8_ TEOREMA DE STEINER O DE LOS EJES PARALELOS
El Teorema de Steiner o de los ejes paralelos permite encontrar el momento de inercia respecto a un eje que no pasa por el CM con el momento de inercia de un eje que pasa por el CM, con la condición que los ejes sean paralelos entre sí.
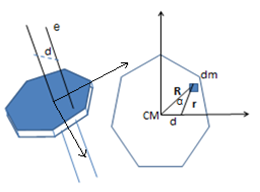
En la figura 9 “d” es la distancia entre ejes paralelos, e es el eje que no pasa por el CM. En la vista de frente, ambos ejes son perpendiculares al papel, R es la distancia de un elemento dm al eje que pasa por el CM, r la distancia de dm al eje paralelo e.
Si aplicamos el teorema del coseno:
r2=R2+d2-2 d R cosα
(α: ángulo comprendido entre R y d)
[latex]I_{CM}=\int R^{2}dm[/latex]
[latex]I_{e}=\int r^{2}dm[/latex]
[latex]I_{e}=\int R^{2}dm+\int d^{2}dm-2d\int R\, cos \alpha\, dm[/latex]
La última integral es nula ya que [latex]R\, cos \alpha=x[/latex] y la [latex]\int x\, dm[/latex], es nula. Esta integral se anula porque es el xcm referenciado al cm. Luego:
[latex]I_{e}=I_{CM}+Md^{2}[/latex]
donde d es la distancia entre ejes paralelos
9_ CÁLCULO DEL MOMENTO CINETICO RESPECTO A UN EJE CUALQUIERA
De acuerdo a lo visto en el modelo de SP, el momento cinético o momento angular de un sistema de n partículas respecto a un eje cualquiera e:
[latex]\vec{L}_{e}=\sum_{i=1}^{n}\vec{r}_{i}\times m_{i}\vec{v}_{i}[/latex]
esta expresión la podemos expresar como:
[latex]\vec{L}_{e}=\sum_{i=1}^{n}\vec{r}_{i-CM}\times m_{i}\vec{v}_{i-CM}+\vec{r}_{CM}\times M\vec{v}_{CM}[/latex]
En esta última expresión el primer término es el momento cinético relativo al CM (momento cinético de spin) y el segundo término es el momento cinético como si toda la masa del SP estuviera en el CM (momento cinético orbital).
Entonces, para nuestro modelo de CR es:
[latex]\vec{L}_{e}=I_{CM}\vec{\Omega }\, +\vec{r}_{CM}\times M\vec{v}_{CM}[/latex]
[latex]\vec{L}_{spin}=I_{CM}\vec{\Omega }[/latex]
[latex]\vec{L}_{orbital}=\vec{r}_{CM}\times M\vec{v}_{C}[/latex]
Tener en cuenta que no siempre [latex]\vec{L}[/latex] y [latex]\vec{\Omega}[/latex] son paralelos. Este paralelismo se cumple sólo para un sistema de ejes particulares denominado eje principales de inercia. En este sistema de ejes, la matriz del tensor de inercia resulta una matriz diagonal.
10_ MOMENTO CINETICO RELATIVO AL CIR
Como el CIR es un punto muy especial, respecto del cual el CR se mueve con rotación pura, vamos a analizar cómo encontrar el momento cinético con respecto a un eje paralelo al baricentro. Apliquemos la expresión hallada anteriormente:
[latex]\vec{L}_{CIR}=I_{CM}\vec{\Omega }\, +\vec{r}_{CM-CIR}\times M\vec{v}_{CM-CIR}[/latex]
Como todos los puntos del CR realizan un movimiento circular (rotación pura) respecto al CIR es:
[latex]\vec{v}_{CM-CIR}=\vec{\Omega}\times \vec{r}_{CM-CIR}[/latex]
es decir
[latex]\vec{v}_{CM-CIR}=\begin{vmatrix} i & j & k\\ 0 & 0 & \Omega \\ -x_{CIR} & -y_{CIR} & 0 \end{vmatrix}[/latex]
[latex]\vec{v}_{CM-CIR}=y_{CIR}\, \Omega\, \breve{i}-x_{CIR}\, \Omega\, \breve{j}[/latex]
Luego el momento cinético orbital se puede escribir:
[latex]\vec{L}_{orbital}=\begin{vmatrix} i & j & k\\ -x_{CIR}& -y_{CIR} &0 \\ y_{CIR}\Omega & -x_{CIR}\Omega &0 \end{vmatrix} M[/latex]
[latex]\vec{L}_{orbital}=(x_{CIR}^{2}+y_{CIR}^{2})M\Omega \, \breve{k}[/latex]
Suponemos en todo este desarrollo que el sistema de coordenadas está ubicado en el CM, con lo cual la posición del CM tiene todas sus coordenadas nulas, y que los ejes son paralelos entre sí. De este modo la expresión entre paréntesis no es otra cosa que la distancia entre ejes elevada al cuadrado. Luego:
[latex]\vec{L}_{CIR}=I_{CM}\, \vec{\Omega }+Md^{2}\, \vec{\Omega }[/latex]
Sacando factor común [latex]\vec{\Omega }[/latex]:
[latex]\vec{L}_{CIR}=(I_{CM}+Md^{2})\vec{\Omega }[/latex]
La expresión anterior entre paréntesis es el momento de inercia del CR respecto del eje paralelo al baricéntrico que pasa por el CIR, resultado que también encontramos aplicando el teorema de Steiner o de los ejes paralelos. Podemos decir entonces que:
[latex]\vec{L}_{CIR}=I_{CIR}\, \vec{\Omega }[/latex]
Como ejercicio de aplicación del teorema de Steiner calculemos el momento de inercia de una varilla delgada que gira alrededor de un eje que pasa por su extremo (obtenga el ICM de la varilla de la tabla anterior) ¿Es lógico el resultado obtenido?
Resumiendo los resultados obtenidos:
[latex]\vec{L}_{e}=I_{CM}\vec{\Omega }\, +\vec{r}_{CM}\times M\vec{v}_{CM}[/latex]
[latex]\vec{L}_{CM}=I_{CM}\, \vec{\Omega }[/latex]
[latex]\vec{L}_{CIR}=I_{CIR}\, \vec{\Omega }[/latex]
11_ LOS MOMENTOS DE INERCIA SON ADITIVOS Y SUSTRACTIVOS
Para encontrar el momento de inercia de un cuerpo complejo podemos considerarlo como la suma o la diferencia, según convenga, de dos cuerpos simples cuyos momentos de inercia conocemos.
Veamos un ejemplo de cada tipo:
a) Cálculo del momento de inercia de un cilindro hueco
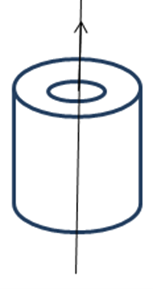
Vamos a encontrar el momento de inercia de un cilindro hueco respecto de su eje baricéntrico de simetría como sustracción o diferencia del momento de inercia del cilindro exterior que supondremos de radio R y el cilindro interior que supondremos de radio r. Sabemos de tablas que el momento de inercia de un cilindro macizo respecto de un eje baricéntrico coincidente con su eje de simetría es [latex]I_{CM}=\frac{1}{2}M R^{2}[/latex].
[latex]I_{CM}^{total}=\frac{1}{2}(M_{ext}R^{2}-M_{int}r^{2})[/latex]
Las masas no son iguales y como los cilindros son homogéneos:
[latex]M=\rho \pi r^{2}h[/latex]
[latex]I_{CM}^{total}=\frac{1}{2}\rho \pi h(R^{4}-r^{4})[/latex]
como las diferencias de potencias pares se pueden factorear
[latex]I_{CM}^{total}=\frac{1}{2}\rho \pi h(R^{2}-r^{2})(R^{2}+r^{2})[/latex]
si estudiamos el significado de la expresión algebraica que encontramos, vemos que lo que está entre barras es la masa del cilindro hueco.
[latex]I_{CM}^{total}=\frac{1}{2}M(R^{2}+r^{2})[/latex] expresión que podemos encontrar tabulada como el momento de inercia del cilindro hueco respecto de su eje de simetría baricéntrico. De esta expresión podemos también encontrar el momento de inercia del aro. Un aro puede ser un cilindro hueco en el cual los radios externo e interno son muy parecidos.
[latex]I_{CM}^{total}=\frac{1}{2}(R^{2}+r^{2})[/latex] es el promedio de los dos radios elevado al cuadrado, pero si son muy parecidos es como si fueran casi iguales entre sí. Podríamos decir que [latex]\frac{1}{2}(R^{2}+r^{2})\approx R^{2}[/latex] con lo cual el momento de inercia del aro es [latex]I_{CM}^{aro}=MR^{2}[/latex].
b) Cálculo del momento de inercia de un conjunto de varilla con esfera
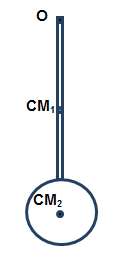
Supongamos tener un cuerpo compuesto formado por una varilla que tiene una esfera pegada en uno de sus extremos. Si la hacemos oscilar alrededor de un eje perpendicular al eje de simetría de la varilla que pase por O, como se muestra en la figura, ¿cómo calculamos el momento de inercia del conjunto respecto de ese eje?
Si los datos de la varilla son: masa de la varilla MV, masa de la esfera ME, la longitud de la varilla L, el radio de la esfera R, los momentos de inercia de la varilla respecto a un eje perpendicular a su eje de simetría que pasa por su CM1 , [latex]I_{CM}^{varilla}=\frac{1}{12}M_{v}L^{2}[/latex] y el momento de inercia de la esfera respecto de un eje baricéntrico CM2 es [latex]I_{CM}^{esfera}=\frac{2}{5}M_{e}R^{2}[/latex].
Los CM de la varilla y de la esfera no coinciden con O, pero podemos aplicar el Teorema de Steiner en ambos cuerpos. Por todo lo expresado
[latex]I_{O}^{total}=I_{CM}^{varilla}+M_{v}(\frac{L}{2})^{2}+I_{CM}^{esfera}+M_{e}(L+R)^{2}[/latex]
El segundo y cuarto término surgen de aplicar el Teorema de los ejes paralelos. La expresión completa es:
[latex]I_{O}^{total}=\frac{1}{12}M_{v}L^{2}+M_{v}(\frac{L}{2})^{2}+\frac{2}{5}M_{e}R^{2}+M_{e}(L+R)^{2}[/latex]
Recomendamos como ejercicio calcular el momento de inercia del conjunto si se cuelga la esfera por su centro de masa. ¿En qué cambian los resultados?
12_ MOMENTO DE INERCIA BARICÉNTRICO DE CUERPOS NO HOMOGÉNEOS Y/O NO SIMÉTRICOS
En principio el cálculo del momento de inercia de cuerpos no homogéneos y/o asimétricos es muy difícil de evaluar ya que la integral triple se complica mucho. Para resolver este problema se propone la siguiente forma.
El momento de inercia baricéntrico es de la forma [latex]I_{CM}=\int d^{2}dm[/latex]. Si la distancia de todos los puntos del CR al eje baricéntrico son todas iguales, esta distancia d es constante. Si la distancia d es constante, entonces la podemos sacar fuera de la integral [latex]I_{CM}=d^{2}\int dm[/latex]. En este caso la integral triple se reduce al cálculo de la masa inercial del CR. Pero, la masa inercial como cantidad de materia se puede medir con una balanza.
Definimos radio de giro baricéntrico (k) a una distancia ficticia que permite calcular el momento de inercia baricéntrico de cualquier cuerpo como ICM=Mk2 donde M es la masa del CR y k el radio de giro baricéntrico. k puede interpretarse como el radio de un aro muy finito que tiene el mismo momento de inercia baricéntrico que el CR en estudio.
En la tabla 1 vemos como ejemplos los radios de giro baricéntrico de cuerpos perfectamente geométricos y homogéneos.
Este concepto permite sortear la dificultad del cálculo de los momentos de inercia de cuerpos de formas complejas, no homogéneos o asimétricos es maravilloso, pero, ¿Cómo podemos hallar el k de estos cuerpos? Veamos a continuación qué pasa si a estos cuerpos los hacemos oscilar colgándolos de un eje.
13_ PENDULO FISICO
Denominamos péndulo físico a un CR que se cuelga de uno de sus puntos y se hace oscilar oscilar. Como su forma puede ser cualquiera lo ejemplificamos con la que se muestra en la figura. En este caso el cuerpo lo colgamos de un eje que pasa por O, punto que denominamos centro de suspensión del CR.
El cuerpo solicitado de este modo, sólo puede moverse con este vínculo alrededor del punto O con rotación pura. Es decir, O se constituye en el CIR para todo el movimiento.
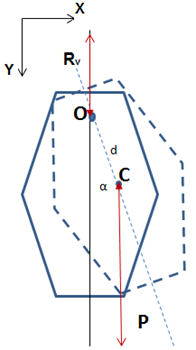
Colocamos entonces nuestro sistema de referencia y nuestro sistema de coordenadas en el punto O. Como la chapa giraría en sentido horario, el eje de abscisas lo invertimos de modo que el eje z quede hacia atrás de la hoja indicando como positivo el sentido horario.
Hacemos el DCL de la chapa. Las dos fuerzas aplicadas sobre la chapa son su peso P y la reacción de vínculo en O Rv.
Escribamos la ecuación fundamental de las rotaciones del CR [latex]\sum_{i=1}^{n}=r_{i-0}\times F_{i}=I_{0}[/latex]
por ser O CIR. De las dos fuerzas actuantes sólo el peso produce torque respecto de O ya que la recta de acción de Rv pasa por O. Llamando d la distancia entre O y el CM.
El torque del peso es:
[latex]\begin{vmatrix} i & j & k\\ d\, sen\alpha & d\, cos\alpha & 0\\ 0& P &0 \end{vmatrix}=P\, d\, sen\alpha \breve{k}[/latex]
Como la chapa tiene una forma irregular, para calcular su momento de inercia baricéntrico aplicaremos el concepto de radio de giro baricéntrico.
ICM=Mk2 Este sería el momento de inercia de la chapa respecto de un eje perpendicular al plano del dibujo que pasa por su CM. Para encontrar el momento de inercia respecto a un eje baricéntrico paralelo al anterior que pasa por el punto O, aplicamos el teorema de Steiner.
I0=Mk2+Md2
Como [latex]\vec{\gamma }=\gamma \, \breve{k}[/latex], la expresión escalar resultante es:
[latex]-P\, d\, sen\alpha =M(k^{2}+d^{2})\gamma[/latex]
Simplificando la masa y reagrupando [latex]-\left[ \frac{g\, d}{k^{2}+d^{2}} \right ]sen\alpha =\gamma[/latex]. Esta expresión se puede aproximar para ángulos menores de 10º a:
[latex]-\left[ \frac{g\, d}{k^{2}+d^{2}} \right ]\alpha =\frac{d^{2}\alpha }{dt^{2}}[/latex]
(el ángulo en radianes es igual a su seno y a su tangente para ángulos pequeños)
El signo negativo indica que cuando α aumenta en sentido anti horario, [latex]\gamma[/latex] aumenta en sentido horario (se oponen). La expresión mencionada es una ecuación diferencial (aparecen [latex]\alpha[/latex] y sus derivadas), homogénea (además del tiempo la única variable es [latex]\alpha[/latex]) y de segundo orden (la derivada de mayor grado es de grado 2).
Esta expresión es característica del movimiento armónico simple (MAS) [latex]-\omega ^{2}x=\frac{d^{2}x}{d\, t^{2}}[/latex]. Esto significa que el movimiento del péndulo físico para pequeñas aberturas puede considerarse un movimiento armónico simple. Igualamos entonces las constantes [latex]\omega ^{2}=\frac{g\, d}{(k^{2}+d^{2})}[/latex] en donde es la pulsación del MAS. Como sabemos que [latex]\omega=\frac{2\pi }{T}[/latex] donde T es el período del movimiento armónico, la expresión para el período del péndulo físico resulta ser
[latex]T=\frac{2\pi }{\sqrt{\frac{g\, d}{(k^{2}+d^{2})}}}[/latex]
o
[latex]T=2\pi \sqrt{\frac{(k^{2}+d^{2})}{g\, d}}[/latex]
Comparamos la expresión del período del péndulo físico con el del péndulo ideal
[latex]T_{ideal}=2\pi \sqrt{\frac{l}{g}}[/latex]
[latex]T_{fisico}=2\pi \sqrt{\frac{(k^{2}+d^{2})}{g\, d}}[/latex]
Si logramos que los períodos sean iguales (sincronismo), como la experiencia la realizamos en el mismo punto de la Tierra g necesariamente según nuestro modelo tiene el mismo valor, entonces [latex]I=\frac{(k^{2}+d^{2})}{d}[/latex]. Como l es la longitud del péndulo simple sincrónico y d es la distancia del punto O, centro de suspensión al CM, son dos valores medibles. Entonces de la expresión anterior podemos calcular el k (radio de giro baricéntrico del CR de forma irregular o no homogéneo o asimétrico).
Este resultado es tan importante para calcular los momentos de inercia que a la longitud del péndulo simple sincrónico con el péndulo físico la llamamos longitud reducida.
¿Qué conclusiones podemos sacar de estos resultados?
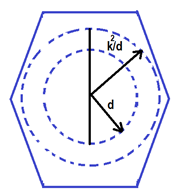
1º.- Todos los puntos que se encuentran a la distancia d del CM, si los tomamos como centro de suspensión, tienen el mismo período. En todos los puntos del cuerpo que se hallan en una circunferencia de radio d, si se cuelga el cuerpo de cualquiera de ellos su período es el mismo.
2º:- Se puede demostrar que todos los puntos que se encuentran en una circunferencia de radio k2/d también tienen igual período. Un punto a la distancia d del CM y otro a la distancia k2/d ubicados en una línea que pasa por el CM se denominan puntos conjugados Están entre sí a la distancia (k2/d) + d (longitud reducida).
Hay otros métodos para encontrar k, algunos de ellos matemáticos y de menor incertidumbre. Sin embargo, este método del péndulo simple sincrónico es conceptualmente más fácil de recordar.
14_ ENERGIA EN EL CR
Energía potencial gravitatoria
En el modelo de Sistema de Partículas, se indicó que para alturas pequeñas con respecto al radio terrestre, la energía potencial gravitatoria es Epg=MghCM expresión que se puede usar para el CR considerando la altura del CM desde el punto de referencia de energía potencial 0.
Energía cinética del CR
Para el mismo modelo se obtuvo una expresión de la energía cinética como la siguiente:
[latex]E_{c}=\frac{1}{2}Mv_{CM}^{2}+\frac{1}{2}\sum m_{i}v_{ir}^{2}+\frac{1}{2}\sum m_{i}v_{it}^{2}[/latex]
El segundo término puede analizarse como una energía de expansión o compresión que en el caso del CR es nula ya que éste no se comprime ni se expande. Si se analiza el tercer término, se concluye que la vi t es una velocidad de rotación alrededor del CM. Su expresión vectorial, para cada partícula es: En esta expresión es el mismo para todo el cuerpo, ya que éste no se deforma y es perpendicular a ri-CM. Por lo tanto,
[latex]v_{rt}^{2}=\Omega^{2}\, v_{i-CM}^{2}[/latex]
Si además se tiene en cuenta que para el CR la sumatoria se transforma en integral y mi en dm, la energía cinética para el CR es:
[latex]E_{c}=\frac{1}{2}Mv_{CM}^{2}+\frac{1}{2}\, \Omega ^{2}\int r_{i-CM}^{2}\, dm[/latex]
La integral (de acuerdo a lo visto) es el momento de inercia baricéntrico. Entonces la expresión puede escribirse [latex]E_{c}=\frac{1}{2}Mv_{CM}^{2}+\frac{1}{2}\,I_{CM}\, \Omega ^{2}[/latex] donde el primer término es la energía cinética de traslación y el segundo término la energía cinética de rotación respecto del CR.
15_ TRABAJO Y ENERGÍA PARA EL CR
La expresión general del teorema del trabajo y la energía para un CR es la misma que para un sistema de partículas.
[latex]\sum W_{fnc}=\Delta E[/latex] (para un cierto sistema la suma de los trabajos de las fuerzas no conservativas, exteriores e interiores al sistema, es igual a la variación de la energía mecánica del mismo).
Observar que:
a) la energía cinética para un CR tiene entonces dos términos, uno referido a la traslación y otro referido a la rotación.
b) el trabajo de fuerzas interiores para un CR es 0 por la condición de rigidez.
16_ ECUACIONES FUNDAMENTALES DE LA DINAMICA DEL CR
1° Ecuación (Ecuación de las traslaciones)
[latex]\sum \vec{F}_{ext}=M\vec{a}_{CM}[/latex]
2° Ecuación (Ecuación de las rotaciones)
[latex]\sum \vec{M}_{CM}^{ext}=I_{CM}\, \vec{\gamma }[/latex]
3° Ecuación (Ecuación de la energía)
[latex]\sum W_{fnc}=\Delta E_{mec}[/latex]
Estas ecuaciones son las que les permiten resolver los problemas en el modelo de CR.
Nota: si se considera el eje instantáneo de rotación el problema se reduce a un movimiento de rotación del cuerpo alrededor de ese eje y por lo tanto no se utiliza la 1º ecuación.
Resumiendo: Para los movimientos siguientes (1 y 2) las condiciones iniciales son las de un cuerpo en reposo.
1.- Traslación Pura
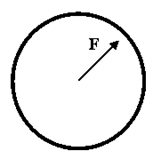
Si la suma de todas las acciones que se ejercen sobre el CR da por resultado que [latex]\sum \vec{F}\neq \vec{0}[/latex] pero [latex]\sum \vec{M}=\vec{0}[/latex], entonces el CR se encuentra en traslación pura. Cuando el cuerpo se mueve en traslación pura, como todos los puntos de mismo se mueven con la misma velocidad y la misma aceleración, es aplicable el modelo de partícula o punto material referido al CM.
2.- Rotación pura
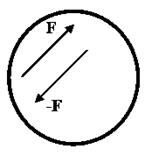
Si la suma de todas las acciones que se ejercen sobre el CR da por resultado que [latex]\sum \vec{F}=\vec{0}[/latex] pero [latex]\sum \vec{M}\neq \vec{0}[/latex], entonces el CR se mueve con rotación pura. En este caso se aplica la segunda ecuación fundamental del CR. La resultante del sistema de fuerzas es una cupla. Se la puede representar con cualquier cupla equivalente, es decir, que tenga el mismo momento. El cuerpo rota alrededor de su CM aunque la cupla se aplique desplazada del mismo como se indica en la figura, ya que las cuplas son vectores libres para un CR.
3.- Rototraslación (condiciones iniciales: no necesariamente en reposo)
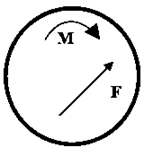
Si, finalmente, el resultado de todas las acciones es [latex]\sum \vec{F}\neq \vec{0}[/latex] y [latex]\sum \vec{M}\neq \vec{0}[/latex], entonces el CR se mueve con rototraslación. En este caso se aplican la 1° y la 2° ecuación fundamental de la dinámica del CR (o la 2º considerando el CIR). La resultante del sistema es una fuerza y una cupla. En este caso el CR rota con rotación pura alrededor del CIR, que puede pertenecer o no al CR.
17_ ACERCA DE LA FUERZA DE ROZAMIENTO
La fuerza de rozamiento por deslizamiento, como ya se vio en el modelo de partícula, puede ser de naturaleza estática o dinámica. La fuerza de rozamiento estática no se conoce a priori y toma valores [latex]\leq \mu _{e}N[/latex]. Donde [latex]\mu _{e}[/latex] es el coeficiente de rozamiento estático y N la reacción normal a las superficies en contacto. La fuerza de rozamiento dinámica, si bien es función de la velocidad con que se desplaza un cuerpo sobre una superficie, se considera que es constante e igual a [latex]\mu _{d}N[/latex] donde [latex]\mu _{d}[/latex] es el coeficiente de rozamiento. Entonces se acepta que cuando existe deslizamiento del punto de contacto la fuerza de rozamiento es dinámica,[latex]f_{rd}=\mu _{d}N[/latex].
Análisis de la fuerza de rozamiento en el deslizamiento
Cuando la velocidad del punto de contacto es distinta de 0, el CR desliza respecto del plano. En este caso, la fuerza de rozamiento a utilizar es la dinámica. Su valor es constante y conocido y se sabe además cuál es su sentido, “se opone al deslizamiento relativo de las superficies en contacto”. Pero el trabajo por deslizamiento está asociado a la distancia resbalada por la superficie del cuerpo. Es decir, se necesita conocer cuánto resbala el punto de apoyo CR respecto de la superficie de apoyo y no cuánto avanza el CM.
Nota: es un error muy frecuente confundir desplazamiento del CM con deslizamiento del punto de contacto.
Análisis de la fuerza de rozamiento de un CR que se mueve rodando sin deslizar.
Cuando la velocidad del punto de contacto es igual a 0, el CR rueda sin deslizar. En este caso, la fuerza de rozamiento que se pone de manifiesto es la estática. Su valor se desconoce y además en el caso de ser distinta de 0 también se desconoce su sentido. Pero, como no hay deslizamiento de una superficie con otra, el desplazamiento del punto de contacto es 0. Por esta razón el trabajo de la fuerza de rozamiento cuando el cuerpo “rueda sin deslizar” es nulo. Esto significa que si la única fuerza no conservativa que puede producir trabajo en el sistema es la fuerza de rozamiento, para este caso, se conserva la energía mecánica del sistema.
Es decir, para un cuerpo con movimiento roto-traslatorio, la fuerza de rozamiento se pone en evidencia de manera de que el CR alcance para algún “t” el estado de “rodar sin deslizar”.
Para suponer un sentido de la fuerza de rozamiento, en el caso de rodar sin deslizar, se proponen los siguientes pasos:
- realizar un DCL del cuerpo en estudio sin colocar todavía la fuerza de rozamiento. Pueden suceder dos cosas: el sistema está en equilibrio ([latex]\sum \vec{F}=\vec{0}[/latex] y [latex]\sum \vec{M}=\vec{0}[/latex]) o el sistema no está en equilibrio ([latex]\sum \vec{F}\neq \vec{0}[/latex] y/o [latex]\sum \vec{M}\neq \vec{0}[/latex]).
- si el cuerpo está en equilibrio dinámico (caso de rodadura en el plano horizontal), la fuerza de rozamiento toma un valor cero. El [latex]\mu _{e}\neq 0[/latex]pero la fuerza de rozamiento es nula.
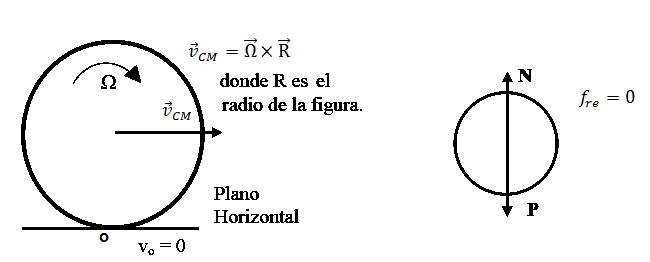
- Si el cuerpo está rodando sin deslizar pero tiene una fuerza neta aplicada en el CM, se debe estudiar qué efecto produce esa fuerza. Este es el caso típico de la rodadura en un plano inclinado o un aro. Se analizan, a continuación, los dos casos posibles: que el cuerpo suba o que el cuerpo baje rodando sin deslizar.
Nota: observar que para ambos casos no se modifica el diagrama de cuerpo libre y, si no actúa la fuerza de rozamiento, hay una resultante aplicada en el CM hacia abajo del plano cuyo valor es [latex]P\, sen\alpha[/latex]).
a) el cuerpo baja

La componente del peso [latex]P\, sen\alpha[/latex], actuando sola, aumenta la velocidad del CM pero no puede cambiar [latex]\vec{\Omega }[/latex]. Si la fr no se pusiera en evidencia el cuerpo resbalaría hacia abajo, ya que la velocidad del punto de contacto debido a la rotación (de módulo [latex]\left |\vec{\Omega }\times \vec{R} \right |[/latex], en sentido contrario a la [latex]\vec{v}_{CM}[/latex]) permanecería constante mientras que la debida a la traslación ([latex]\vec{v}_{CM}[/latex]) aumentaría. Por esta razón la fr debe ser hacia arriba de modo de aumentar la velocidad de rotación [latex]\vec{\Omega }[/latex] y al mismo tiempo oponerse al aumento de la [latex]\vec{v}_{CM}[/latex], de modo que para todo tiempo se cumpla que [latex]\vec{v}_{CM}=\vec{\Omega }\times \vec{r}[/latex].
b) hacer el análisis para cuando el cuerpo sube.
Nota: Si el momento de inercia se considerara como un escalar, siempre L e I serían paralelos, cosa que no es cierta (ver, por ejemplo textos de Roederer, Alonso-Finn). En cambio el modelo que asocia a I con una transformación lineal, se corresponde con la experimentación. Considerando un sistema de ejes cartesianos ortogonales la matriz es diagonalizable, obteniéndose los correspondientes autovalores, que se denominan (para este caso) momentos principales de inercia Ixx, Iyy, Izz. Así Lx =Ixx Ωx , Ly =Iyy Ωy, Lz= Izz Ωz . A la base asociada al conjunto de autovalores se los denomina ejes principales de inercia. Un caso particular de ejes principales de inercia son los ejes de simetría del cuerpo. Si A es un punto fijo al laboratorio o se mueve con velocidad constante respecto al centro de masa del CR, y aplicando el teorema de ejes paralelos o de Steiner, se pueden reescribir las anteriores ecuaciones como LAx =IAxx Ωx , etc. Debido a que la matriz de esta transformación tiene propiedades especiales, frente a un cambio de coordenadas, dicha matriz se denomina tensor. En este caso en particular, el “tensor de inercia”.
18_ APLICACIONES DE DINÁMICA DEL CUERPO RÍGIDO
1.- Revisión de la máquina de Atwood.
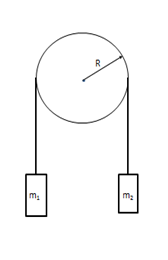
Supongamos una polea apoyada en un eje horizontal con rodamientos sin fricción de radio R = 0,10m y momento de inercia baricéntrico ICM = 1,3.10-3 kg.m2, de la cual penden dos cuerpos de masas m1 = 0,50 kg y m2 = 0,55 kg respectivamente como se muestra en la figura.
Si el sistema se libera partiendo del reposo
a.- Encontrar la aceleración angular de la polea
b.- Calcular la aceleración del bloque mayor.
c.- Cuando m2 baja 1 m encontrar la velocidad angular de la polea y la velocidad del bloque menor.
Para resolver el problema debemos acordar que la polea y el hilo se mueven solidariamente (no hay movimiento relativo entre ellos). Como siempre antes de resolver debemos preguntarnos cómo se mueve la polea. Recordemos que es una polea fija. ¿Podemos considerar que la polea es un cilindro perfecto? ¿Por qué?
¿Podemos suponer que las tensiones de ambos lados son iguales ¿Por qué?
2.- Un cilindro de masa M y radio R cuelga de dos hilos enrollados como se muestra en la figura. Si al sistema se lo suelta partiendo del reposo calcular:
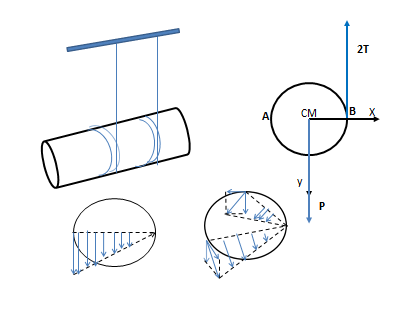
a.-La tensión [latex]\vec{T}[/latex] en cada hilo y la aceleración del CM del cilindro [latex]\vec{a}_{CM}[/latex]
b.- Para un tiempo t después de soltarlo calcular [latex]\vec{v}_{CM}[/latex], [latex]\vec{v}_{A}[/latex]
y [latex]\vec{v}_{B}[/latex].
a) El cilindro gira en sentido anti horario. Los hilos y el cilindro se mueven solidarios. Es decir, la velocidad de los puntos de contacto del cilindro coincide instante a instante con los de los hilos.
Por otro lado, los puntos de los hilos que se encuentran desde el techo hasta la posición del punto B permanecen en reposo V = 0. Por eso, los puntos de la generatriz horizontal del cilindro que pasa por el punto B son CIR.
Las velocidades de los puntos de contacto (todas en sentido anti horario, van aumentando del punto B hasta el punto A para luego disminuir en módulo siguiendo la circunferencia de contacto
Partimos de las ecuaciones fundamentales de la dinámica del CR:
[latex]\sum \vec{F}_{ext}=M\vec{a}_{CM}[/latex]
[latex]\sum \vec{r}\, \times \vec{F}=I_{CM}\, \vec{\gamma }[/latex]
En este caso y con el sistema de coordenadas elegido en la segunda figura:
[latex]y)\: P-2T=M\, a_{CM}[/latex]
[latex]z)\: 2TR=I_{CM}\, \gamma[/latex]
Por condición de vínculo:
[latex]\vec{v}_{CM}=\vec{\omega }\, R[/latex]
Luego:
[latex]\vec{a}_{CM}=\vec{\gamma}\, R[/latex]
reemplazando esta expresión en z):
[latex]2TR=\frac{1}{2}MR^{2}\, \frac{a_{CM}}{R}[/latex]
[latex]T=\frac{1}{4}M\, a_{CM}[/latex]
Reemplazando en y)
[latex]P-2T=4T[/latex]
Luego
[latex]T=\frac{P}{6}[/latex] y [latex]a_{CM}=\frac{2}{3}\, g[/latex]
[latex]\vec{T}=\frac{Mg}{6}\, \breve{j}[/latex] y [latex]\vec{a}_{CM}=\frac{2}{3}\, g\, \breve{j}[/latex]
b) El cálculo de las velocidades del CM y de los puntos A y B en el tiempo t, vemos que como la aceleración del CM es 2/3 g es constante, la velocidad del CM será instante a instante igual a:
[latex]v_{CM}=\frac{2}{3}g\, t[/latex]
y como [latex]\gamma =\frac{a_{CM}}{R}[/latex]
[latex]\gamma =\frac{\frac{2}{3}g}{R}[/latex]
como la aceleración angular es constante:
[latex]\vec{\omega }=\vec{\gamma }\, t[/latex]
[latex]\vec{v}_{CM}=\frac{2}{3}g\, t\, \breve{j}[/latex]
[latex]\vec{v}_{A}=\vec{v}_{CM}+\vec{\Omega }\times \vec{r}_{A-CM}[/latex]
[latex]\vec{v}_{A}=\frac{2}{3}gt\, \breve{j}+\begin{vmatrix} i & j & k\\ 0 & 0 & \Omega \\ -R & 0 & 0 \end{vmatrix}[/latex]
operando
[latex]\vec{v}_{A}=\frac{4}{3}gt\, \breve{j}[/latex]
de igual modo
[latex]\vec{v}_{B}=\vec{v}_{CM}+\vec{\Omega }\times \vec{r}_{B-CM}[/latex]
[latex]\vec{v}_{B}=\frac{2}{3}gt\, \breve{j}+\begin{vmatrix} i & j & k\\ 0 & 0 & \Omega \\ R & 0 & 0 \end{vmatrix}[/latex]
resolviendo
[latex]\vec{v}_{B}=\vec{0}\, \, m/s[/latex]
3.- Un yo-yo se encuentra en reposo sobre una mesa horizontal y está en libertad de rodar, ver figura. Se ejerce sobre el hilo del yo-yo una suave tracción hacia arriba con un ángulo q de modo que el yo-yo ruede sin resbalar.
Hallar una expresión para la aceleración del CM en función de los datos.
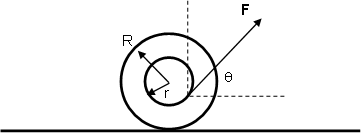
Posibles preguntas antes de empezar a resolver el problema:
- ¿Va a avanzar hacia la derecha o hacia la izquierda?
- ¿Cuál es el momento de inercia del yo-yo?
- ¿Cuál es el sentido de la fuerza de rozamiento?
- ¿Es rozamiento estático o dinámico?
- ¿Cuál es el punto de aplicación de F? ¿Este punto, es siempre el mismo o cambia con el ángulo?
- ¿Es necesario que el observador sea inercial?
- ¿Qué puntos notables puede elegir como origen del sistema de coordenadas?
- ¿Hacia dónde conviene poner positivos los ejes?
- ¿Qué correcciones debe hacer si desea trabajar con sistema levógiro o izquierdo?
Recomendaciones para la resolución de problemas de dinámica del CR:
Un movimiento rototraslatorio podemos pensarlo como una suma de dos movimientos puros, uno de traslación y otro de rotación. Esta superposición de dos movimientos “puros”, equivale al movimiento rototraslatorio real del cuerpo. Para ambos movimientos aplicamos las leyes correspondientes o sea las dos ecuaciones universales vistas anteriormente.
Pero hay que tener cuidado respecto a la traslación, hay una diferencia entre partícula y CR ya que para partícula uno calcula su velocidad y para CR su campo de velocidades. Lo que sucede es que la 1º ecuación universal se aplica al centro de masa y, por lo tanto, la traslación la enfocamos en ese punto.
También es posible, referenciar el movimiento respecto al CIR como un movimiento de rotación instantánea.
Independientemente de la estrategia seleccionada de resolución, hay algunas recomendaciones que es necesario tener en cuenta:
1) Definir los sistemas de referencia y de coordenadas a utilizar.
2) Hacer el diagrama de cuerpo libre del CR.
3) Plantear las ecuaciones universales.
4) Plantear la relación entre la aceleración angular y la aceleración del centro de masa, y otras relaciones dadas por los vínculos del sistema.
5) Resolver el sistema de ecuaciones (sin hacer reemplazos numéricos previos).
6) Analizar la coherencia y compatibilidad del resultado final, con los posibles movimientos del sistema. Por ejemplo, si se calcula una fuerza de rozamiento estática, verificar que sea menor o igual que la fuerza de rozamiento estática máxima.
Resolución del problema:
1) Planteo del sistema de referencia y ejes de coordenadas:
Como el CM se mueve en forma rectilínea elegimos un típico sistema de coordenadas cartesiano x-y con, por ejemplo, el eje x paralelo al piso. El origen de coordenadas podría estar en el CM o en el CIR (en realidad podría estar en cualquier lado, pero esos son los puntos más simples para el planteo y los cálculos).
El sistema de referencia podría ser fijo a la Tierra (Laboratorio) o “subido” al yo-yo. En este último caso, tendríamos que considerar una fuerza ficticia ya que el sistema estaría acelerado.
Elegimos un sistema de referencia fijo a Tierra, ya que no tendríamos mayores ventajas en elegir un SRNI fijo al yo-yo.
En cuanto a la ubicación del origen de coordenadas, es indistinto ubicarlo en el CM o en el CIR, cada uno tiene sus pros y contras:
| Ventajas | |
| Origen en el CM | El radio menor r, es siempre perpendicular a F, ya que F está aplicada por una cuerda que es tangente al disco interno del yo-yo. No hace falta aplicar Steiner. |
| Origen en el CIR | La fuerza de rozamiento no hace torque con respecto a ese punto. |
Finalmente, elegimos el origen en el CM en un sistema fijo a Tierra.
Hasta acá, el planteo es muy similar al que hacíamos para masas puntuales. Pero ahora hay un agregado, hay que indicar el sentido de giro positivo en nuestro sistema de coordenadas. Pero ese sentido quedó establecido al definir los sentidos positivos de los versores [latex]\breve{i}[/latex] y [latex]\breve{j}[/latex]. Al definir nuestros ejes positivos en un sentido dado, queda indicado el eje z y el sentido de giro de tal manera de obtener una terna derecha (regla de la mano derecha).
Por ejemplo, en nuestro caso queda:
[latex]\breve{i}\times \breve{j}=\breve{k}[/latex]
El versor [latex]\breve{k}[/latex], es positivo y perpendicular al plano (x-y) y apunta hacia el lector. Aplicando la regla de la mano derecha, vemos que el sentido de giro positivo es el antihorario mostrado en la figura. Observar que, si hubiésemos elegido el eje “y” positivo hacia abajo, entonces, el sentido de giro positivo sería el horario.
Si bien el origen de coordenadas está ubicado en la posición del CM, el sistema se encuentra fijo a Tierra. Lo que analizamos es una “foto” en la cual, en ese instante, el origen del sistema fijo a Tierra coincide con la posición del CM del yo-yo.
De esta manera, ya nos queda definida nuestra referencia con respecto a la cual vamos a considerar positivos o negativos los momentos de las fuerzas.
2) Diagrama de Cuerpo Libre (DCL):
DCL para analizar las fuerzas y los momentos
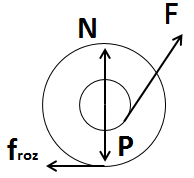
El sentido de la fuerza de rozamiento:
No siempre se puede deducir a priori el sentido de la Froz. En algunos casos, cuando hay datos suficientes, se puede pensar físicamente de forma cualitativa y “anticipar” efectivamente el sentido de la misma.
Imaginemos por un momento que la superficie de apoyo no tiene rozamiento y hagamos actuar a la fuerza F ¿Cómo se movería el yo-yo?
En este caso, no es tan simple el análisis. Una posible situación, que la fuerza F acelere el cuerpo hacia la derecha. Como el enunciado nos dice que el CR rueda sin resbalar y el torque de la fuerza F produce una aceleración angular antihoraria, debería haber otro torque con módulo mayor que tenga sentido horario. Por lo tanto en el caso de haber rozamiento, concluimos que el probable sentido de la fuerza de rozamiento debe ser hacia la izquierda, de modo que se cumpla que la suma de torques produzca una rotación horaria.
Cuando apliquemos las ecuaciones universales vamos a corroborar este razonamiento físico que realizamos en forma cualitativa.
3) Ecuaciones universales:
De las ecuaciones vectoriales y de acuerdo a la terna seleccionada:
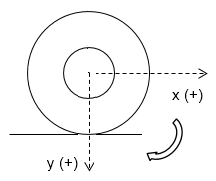
[latex]y) -N+mg=0[/latex]
[latex]x) F_{x}-f_{roz}=m\, a_{CM}[/latex]
[latex]x) Fcos\theta -f_{roz}=m\, a_{CM}[/latex]
Vamos a plantear las ecuaciones de momento con dos metodologías. Ambas son válidas y tienen sus pros y contras que veremos a continuación. Obviamente, ambos métodos deben conducirnos al mismo resultado final.
| Cálculo trabajando en componentes cartesianas | Cálculo trabajando en módulo |
| [latex]\sum \vec{M}_{CM}^{ext}=I_{CM}\, \vec{\gamma }[/latex]
------------------------------------------------------------------- [latex]\vec{r}=(-rsen\theta ;-rcos\theta ;0)[/latex] [latex]\vec{F}=(Fcos\theta ;-Fsen\theta ;0)[/latex] [latex]\vec{r}\times \vec{F}=(0)\breve{i}+(0)\breve{j}+(rsen\theta \, Fsen\theta +rcos\theta \, Fcos\theta)\breve{k}[/latex] [latex]\vec{r}\times \vec{F}=(rF)\, \breve{k}[/latex] ------------------------------------------------------------------- [latex]\vec{r}=(0;R;0)[/latex] [latex]\vec{f}_{roz}=(-f_{roz};0;0)[/latex] [latex]\vec{r}\times \vec{F}=(0)\breve{i}+(0)\breve{j}+(Rf_{roz})\breve{k}[/latex] [latex]\vec{r}\times \vec{F}=(Rf_{roz})\breve{k}[/latex] ------------------------------------------------------------------- [latex]\sum \vec{M}_{CM}^{ext}=(-rF+Rf_{roz})\breve{k}=I_{CM}\, \vec{\gamma }[/latex]
|
[latex]\sum \vec{M}_{CM}^{ext}=I_{CM}\, \vec{\gamma }[/latex]
En este caso, se llega a la ecuación de torque mediante un análisis físico previo del sistema. El análisis consiste en evaluar los siguientes aspectos: > Si la fuerza es perpendicular a la distancia para todo tiempo, entonces, podemos reemplazar el producto vectorial por el producto de los módulos.
> El signo del torque se lo asignamos viendo en qué sentido tiende a hacer girar al cuerpo cada uno de los torques. Si la tendencia del torque es a hacerlo girar en contra de lo que definimos positivo en nuestro sistema de coordenadas, entonces, el toque es negativo y viceversa.
En nuestro caso, como F está aplicada mediante un hilo enrollado, la fuerza es tangente al disco interno del yo-yo y por lo tanto en todo momento es perpendicular al radio menor “r”. También, R y froz son siempre perpendiculares. Por otro lado, el momento de [latex]\vec{F}[/latex] tiende a hacer girar al disco en sentido antihorario que, según nuestro sistema de coordenadas, es negativo. Por el contrario, la froz tiende a hacerlo girar en sentido horario con respecto al CM, con lo cual, el signo del momento es positivo. En definitiva nos termina quedando la misma ecuación de torques que por el método puramente analítico. [latex]\sum {M}_{CM}^{ext}=-rF+Rf_{roz}=I_{CM}\,{\gamma }[/latex] |
4) Relación entre γ y la aCM
Para poder vincular las ecuaciones de Newton con las de torque, tenemos que vincular la aceleración angular con la lineal del CM.
En una rototraslación, la relación entre la aceleración lineal de un punto del CR y su aceleración angular puede ser cualquiera, siempre y cuando cumpla con la condición de rigidez.
Pero cuando el cuerpo está vinculado, por ejemplo, en contacto con una superficie, girando alrededor de un eje, etc. las posibilidades de movimiento se restringen y se pueden escribir relaciones específicas entre el movimiento de rotación y el de traslación.
En nuestro caso, el cuerpo está vinculado a una superficie, no se puede desplazar para cualquier lado, solo se desplaza a la izquierda o a la derecha. Incluso, en este caso el vínculo es aún mayor, ya que no solo está limitada la dirección de su movimiento, además el yo-yo rueda sin deslizar. Eso quiere decir que el CR realiza, instante a instante, una rotación pura alrededor del punto de contacto con el piso (CIR). En particular, para el centro de masa se cumple que:
[latex]\vec{a}_{CM}=\vec{\gamma }\times \vec{R}_{CIR-CM}[/latex]
Veamos más de cerca el origen de esta ecuación y sus signos. Como hicimos antes, también ahora podemos optar por un método analítico formal u otro más “físico-práctico”.
5) Análisis y resolución del problema:
| Método analítico formal | Método físico-práctico |
| Partiendo de la relación general de velocidades para los cuerpos rígidos, podemos escribir para cualquier par de puntos:
[latex]\vec{v}_{p}=\vec{v}_{q}+\vec{\Omega }\times \vec{r}_{q-p}[/latex] Dónde p y q son dos puntos cualesquiera del cuerpo rígido, y la nomenclatura: q-p, significa que el vector tiene origen en el punto q y extremo en p. Derivando con respecto al tiempo, obtenemos la relación de aceleraciones: [latex]\vec{a}_{p}=\vec{a}_{q}+\vec{\gamma }\times \vec{r}_{q-p}+\vec{\Omega }\times \vec{v}_{q-p}[/latex] Pero [latex]\vec{v}_{q-p}[/latex] es la velocidad transversal del punto p, el cual está haciendo una rotación pura a una distancia [latex]\vec{r}_{q-p}[/latex] del punto q, con lo cual se puede escribir como: [latex]\vec{a}_{p}=\vec{a}_{q}+\vec{\gamma }\times \vec{r}_{q-p}+\vec{\Omega }\times (\vec{\Omega }\times \vec{r}_{q-p})[/latex] [latex]\vec{v}_{q-p}=\vec{\Omega }\times \vec{r}_{q-p}[/latex] El último término representa la aceleración centrípeta cuya dirección está en el eje “y”, lo cual no es relevante para el movimiento de traslación que estamos analizando, el cual es sólo en el eje “x”. Así que los términos de aceleración que tienen componente en el eje “x” son: [latex]\vec{a}_{p}=\vec{a}_{q}+\vec{\gamma }\times \vec{r}_{q-p}[/latex] A los puntos genéricos p y q, los particularizamos para nuestro problema, uno va a ser el CM y el otro el CIR. En realidad es indistinto, y se puede elegir cualquiera, pero para ser coherentes con nuestro origen de coordenadas, vamos a elegirlos de tal manera que el vector [latex]\vec{r}_{q-p}[/latex] tenga origen en el CM, al igual que nuestro sistema de coordenadas, con lo cual quedaría que q = CM y p = CIR. [latex]\vec{a}_{CIR}=\vec{a}_{CM}+\vec{\gamma }\times \vec{r}_{CM-CIR}[/latex] Dónde: [latex]\vec{a}_{CM}=\vec{0}\, \, m/s^{2}[/latex] (solo en el eje x, recordemos que dejamos de lado al término de la aceleración centrípeta en dirección [latex]\breve{j}[/latex]) [latex]\vec{r}_{CM-CIR}=R\, \breve{j}[/latex] [latex]\vec{0}=\vec{a}_{CM}+\vec{\gamma }\times R\, \breve{j}[/latex] Haciendo el producto vectorial, y teniendo en cuenta que tiene solo componente en [latex]\breve{k}[/latex]: [latex]{\gamma }\: \breve{k}\times R\, \breve{j}=\gamma R\: \breve{i}[/latex] Con lo cual queda: [latex]\vec{a}_{CM}=\gamma R\: \breve{i}[/latex] |
Analizando las posibilidades de movimiento de nuestro sistema, podemos ver que el yo-yo puede avanzar hacia la izquierda o hacia la derecha.
Además, como rueda sin deslizar (acá está la clave), si avanza hacia la derecha lo hará rotando en sentido horario y viceversa. Teniendo en cuenta lo anterior, y que en el sistema de coordenadas elegido, “hacia la derecha” significa sentido positivo de las “x” y que, giro “horario”, tiene signo positivo, se ve cómo es la relación de signos entre aCM y la aceleración angular γ. Ya que elegimos la terna “a conveniencia”, es mejor seleccionar una en que acm y γ sean positivas. Aclaración: No perder de vista que esta relación de signos depende pura y exclusivamente de cómo elegimos nuestra terna derecha. Además, como γ y R son perpendiculares entre sí (uno es en [latex]\breve{k}[/latex] y el otro en [latex]\breve{j}[/latex]), podemos reemplazar el producto vectorial por: aCM = γ R Con lo cual llegamos a la relación buscada. Teniendo en cuenta que el término de aceleración centrípeta no lo evaluamos para el centro de masa. (Pero si lo deberíamos evaluar si se tratase de otro punto del CR). NOTA: Tener bien definido el sistema de coordenadas. Esto implica, determinar con precisión la terna derecha que nos permita saber unívocamente tanto los sentidos positivos de los ejes, como los de las rotaciones. |
Resumiendo, agrupando las ecuaciones que son relevantes para resolver este problema, tenemos el siguiente sistema de tres ecuaciones con tres incógnitas: γ, aCM y froz.
1º ecuación universal, proyección sobre X
[latex]F cos \theta- f_{roz}=m\, a_{CM}[/latex]
2º ecuación universal con respecto al CM
[latex]-rF+Rf_{roz}=I_{CM}\, \gamma[/latex]
Relación entre la aceleración lineal y la angular: (ecuación de vínculo)
aCM = γ R
Los signos de las fuerzas, los momentos, y las aceleraciones, están de acuerdo a la terna derecha elegida como sistema de coordenadas.
Resolviendo el sistema de ecuaciones, llegamos a la siguiente expresión para la aceleración angular:
[latex]\gamma =\frac{RF(cos\theta -\frac{r}{R})}{I_{CM}+mR^{2}}[/latex]
El denominador es siempre positivo, con lo cual el signo de γ viene dado por el signo de [latex]\left (cos\theta -\frac{r}{R} \right )[/latex] con lo cual si:
[latex]cos\, \theta > \frac{r}{R} \: \Rightarrow \: \gamma > 0[/latex]
[latex]cos\, \theta = \frac{r}{R} \: \Rightarrow \: \gamma = 0[/latex]
[latex]cos\, \theta < \frac{r}{R} \: \Rightarrow \: \gamma < 0[/latex] no es el resultado esperado pues es un número positivo o cero
En este caso debemos revisar en el DCL el sentido de y realizar un análisis del vínculo, lo que resultará en:
[latex]\gamma =\frac{RF(\frac{r}{R}-cos\theta)}{I_{CM}+mR^{2}}[/latex]
Las relaciones anteriores muestran que existe un ángulo crítico a partir del cual el yo-yo avanza hacia la izquierda o hacia la derecha. Por ejemplo, si el coseno toma un valor próximo a 1 (su valor máximo) la aceleración angular será positiva. Y, según nuestro sistema de referencia, aceleraciones angulares positivas significan giros en sentido horario, lo que implica que el yo-yo se desplazará hacia la derecha. Por el contrario, para ángulos que sean mayores al ángulo crítico, por ejemplo, cercanos a π/2, el coseno tomará valores menores que r/R; esto significa que el yo-yo se desplazará hacia la izquierda, girando en sentido anti-horario.
El ángulo crítico se obtiene despejándolo de la última expresión:
[latex]\theta _{critico}= cos^{-1}(r/R)[/latex]
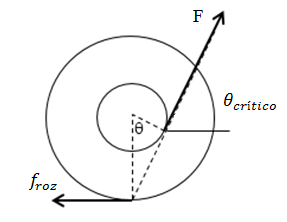
En el esquema, se ve el yo-yo cuando el hilo tira con el ángulo crítico.
Para ese ángulo, la proyección de F pasa por el CIR haciendo nulo el torque de F con respecto a ese punto.
Gráficamente, también se puede ver que el ángulo crítico es justamente cuando, [latex]cos\, \theta =r/R[/latex]
Si en vez del CM, nos parásemos en el CIR, se ve claramente que cuando F tira con el ángulo crítico, la suma de momentos con respecto al CIR es cero. Asimismo, tomando como centro de momentos el centro de masa, cuando F tira con el ángulo crítico, la suma de torques nuevamente es cero, ya que el torque de F con respecto al CM es igual (en módulo) y contrario (en signo), al realizado por la froz. Esta congruencia de resultados, muestra que la dinámica del movimiento no depende del centro de momentos que elijamos para resolver el problema.
La fuerza de rozamiento: si de las tres ecuaciones de movimiento, en vez de despejar la aceleración angular, despejamos la froz, obtenemos la siguiente expresión:
[latex]f_{roz}=\left (\frac{F}{3} \right )\left ( cos\, \theta +2\left ( \frac{r}{R} \right ) \right )[/latex]
Con [latex]0\leq \theta \leq \pi /2[/latex], la froz es siempre positiva o sea apunta hacia la izquierda.
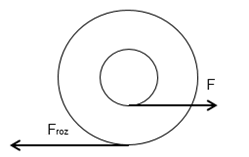
[latex]f_{roz}=\left (\frac{F}{3} \right )\left (1 +2\left ( \frac{r}{R} \right ) \right )[/latex]
Avanza hacia la derecha y giro horario
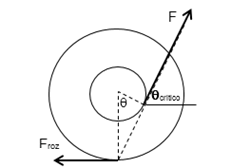
[latex]f_{roz}=F\left ( \frac{r}{R} \right )[/latex]
No avanza, salvo que [latex]F\, cos\, \theta > \mu N[/latex]
en cuyo caso desliza sin rodar
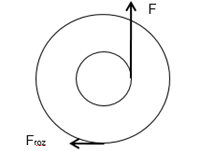
[latex]f_{roz}=F\left ( \frac{2}{3} \right ) \left ( \frac{r}{R} \right )[/latex]
Avanza hacia la izquierda y giro antihorario
El planteo desde el CIR:
Si en vez de elegir el CM, se hubiese elegido el CIR como centro de momentos, la Froz no hace momentos y hay que referir la F al CIR.
La aplicación de las ecuaciones universales queda:
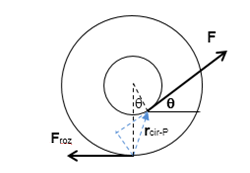
[latex]\vec{r}_{CIR-P}\times \vec{F}=I_{CIR}\, \vec{\gamma }[/latex]
Donde [latex]\vec{r}_{CIR-P}[/latex] se puede escribir como:
[latex]\vec{r}_{CIR-P}=(r\, sen\, \theta ;-R+r\, cos\, \theta;0 )[/latex]
Y [latex]\vec{F}[/latex] como:
[latex]\vec{F}=(Fcos\, \theta;-Fsen\, \theta;0 )[/latex]
[latex]\vec{r}_{CIR-P}\times \vec{F}=(r\, sen\, \theta ;-R+r\, cos\, \theta;0 )\times (Fcos\, \theta;-Fsen\, \theta;0 )[/latex]
[latex]\vec{r}_{CIR-P}\times \vec{F}=F(r-R\, cos\, \theta )\, \breve{k}[/latex]
[latex]F(r-R\, cos\, \theta )\, \breve{k}=(I_{CM}+mR^{2})\, \vec{\gamma }[/latex]
[latex]\vec{\gamma }=\frac{RF(-\frac{r}{R}+cos\, \theta )}{(I_{CM}+mR^{2})}\, \breve{k}[/latex]
[latex]\vec{\gamma }=\frac{F(-r+R\, cos\, \theta )}{(I_{CM}+mR^{2})}\, \breve{k}[/latex]
De la cual sacamos R factor común y obtenemos la misma expresión que habíamos hallado anteriormente:
[latex]\vec{\gamma }=\frac{RF(-\frac{r}{R}+cos\, \theta )}{(I_{CM}+mR^{2})}\, \breve{k}[/latex]
Observar que, en este caso, no tuvimos necesidad de utilizar la ecuación de la traslación para obtener [latex]\vec{\gamma }[/latex], pues ambas ecuaciones no forman un sistema, es como si estuvieran desacopladas.
19_SITUACIÓN PROBLEMÁTICA ESPECIAL DE INTEGRACIÓN METODOLÓGICA
¿PUNTOS DE LA BARRA MÁS ACELERADOS QUE PARTÍCULAS EN CAÍDA LIBRE?
Antecedentes:
En un tema de examen se tomó el siguiente enunciado:
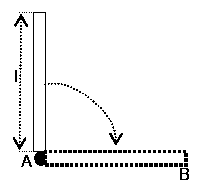
La varilla rígida, fina, homogénea, de masa m y longitud l, se encuentra inicialmente en reposo, en posición vertical. Está articulada en el extremo A (vínculo de eje fijo normal al papel). Se la deja en libertad y gira alrededor de A hasta alcanzar la posición horizontal. Decir y justificar para el instante final, si es verdadero o falso, lo siguiente:
a) El módulo de la aceleración total del centro de masa es igual al módulo de la aceleración total del extremo B.
b) El módulo de la aceleración total del centro de masa es mayor que el módulo de la aceleración de la gravedad.
c) La componente de aceleración radial del centro de masa es mayor que el módulo de la aceleración de la gravedad.
d) Las aceleraciones totales del centro de masa y del extremo B son vectores paralelos.
Introducción:
Realicemos una experiencia exploratoria de esta situación problemática y paradójica.
Si a una partícula se la deja caer libremente en el vacío, en las proximidades de la superficie terrestre, independientemente de su masa, va a caer con MRUV con aceleración de módulo 9,8 m/s2.
Sin embargo, la teoría de cuerpo rígido aplicada a una varilla que puede caer desde la posición vertical (o a partir de un cierto ángulo por sobre la horizontal) articulada en uno de sus extremos predice que el módulo de la aceleración del centro de masa es mayor que g y que la aceleración transversal del otro extremo puede superar la aceleración de la gravedad. Se recomienda ver el video del desarrollo de este problema.
Veamos cómo “vuelan”, se despegan de la varilla de madera los “M&M” o “Rocklets” en el siguiente video YouTube:
http://www.youtube.com/watch?v=d1i4Gh-4NGs
He aquí dos instantáneas del mismo.

La primera con la varilla horizontal atada con un hilo que luego se cortará para dejarla libre en movimiento, articulada en la tabla que está junto al muchacho.

La segunda señala la posición que toman los “M&M” (línea recta horizontal con los mismos cayendo con aceleración de la gravedad) y la posición de la varilla rígida. Se aprecia que en los puntos cercanos al extremo su aceleración tangencial es mayor que la aceleración de la gravedad.
Podemos mencionar un problema de aplicación en ingeniería civil: “demolición por implosión de chimeneas” (falling chimney), por ejemplo en YouTube vemos:
La chimenea aún no a tocado el piso, tampoco se le han colocado cargas explosivas en su parte media, sin embargo está quebrada, ¿Por qué?

La chimenea posee una cumbrera que está sin anclaje. Entonces en algún momento vemos que se despega de la punta (Como los “M&M o “Rocklets”)

