Indice

1. Introducción
2. Potencia
3. Energía potencial y fuerzas conservativas
4. Fuerzas centrales
5. La energía cinética
6. Problemas

Trabajo y Energía

 1_ INTRODUCCIÓN

 Consideremos una partícula sobre la que actúa una fuerza  y describe la curva indicada en la figura. Vamos a definir el trabajo mecánico de la fuerza primero en forma matemática, y después buscaremos su interpretación física.

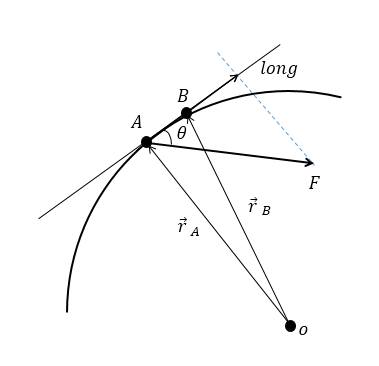
Para ello, consideremos un elemento infinitesimal de la curva, y sea [latex]d\vec{r}[/latex] el desplazamiento de la partícula. Definimos el diferencial de trabajo dW como:

[latex]dW=\vec{F}\cdot d\vec{r}[/latex]

El producto entre la fuerza y el diferencial de desplazamiento es un producto escalar. Obtenemos entonces una primera conclusión: así definido, el trabajo es una magnitud escalar.

Ahora integramos y el trabajo mecánico W será:

[latex]W=\int_{A}^{B}\vec{F}\cdot d\vec{r}[/latex]

El trabajo es, por lo tanto, una integral de línea, es decir, la integral de una función cuyos valores se calculan sobre una curva.

Ahora bien, el producto escalar puede calcularse de distintas formas. Una de ellas consiste en el producto de los módulos multiplicado por el coseno del ángulo θ comprendido entre los vectores. Entonces

[latex]W=\int_{A}^{B}F cos\theta dr[/latex]

Aquí podemos encontrarnos con un caso particular que permite simplificar los cálculos. Supongamos que:

• – el módulo de la fuerza es constante
• – el ángulo entre la fuerza y el desplazamiento también es constante.

Entonces la integral se reduce a:

[latex]W=F\Delta rcos\theta[/latex]

De todas formas, recordemos que la fórmula precedente no es universalmente válida, sólo puede aplicarse bajo las hipótesis indicadas.

Pregunta: ¿Para qué fuerza, que ya conocemos, tal fórmula no es aplicable?

Respuesta: no puede aplicarse, por ejemplo, para la fuerza elástica debido a que se trata de una fuerza variable con la posición.

Pregunta: ¿Qué representa [latex]F cos\theta[/latex]?

Respuesta: representa la componente de la fuerza sobre el eje tangente a la trayectoria de la partícula.

Pregunta: si sobre una partícula se aplican varias fuerzas, ¿Cómo se calcula el trabajo total sobre dicha partícula?

Respuesta: a partir de su definición se ve que el trabajo total será la sumatoria de los trabajos de cada una de las fuerzas individuales.

Pregunta: ¿En qué unidades se mide el trabajo?

Respuesta: en el sistema S.I. se mide en joule (J), de forma tal que 1J = 1N. 1m.

Pregunta: ¿El trabajo es siempre un número positivo?

Respuesta: no. El signo del trabajo vendrá determinado por el signo del . Por lo tanto, el trabajo será positivo para [latex]cos\theta< \frac{\pi }{2}[/latex]. Y será nulo si [latex]\theta=\frac{\pi }{2}[/latex], de donde concluimos que una fuerza perpendicular al desplazamiento no realiza trabajo.

2_ POTENCIA

Consideremos dos máquinas cuya labor consista en elevar un cierto peso hasta una altura h. Las dos máquinas estarán, por lo tanto, efectuando el mismo trabajo.

Pero ahora supongamos que una de las máquinas realiza dicho trabajo con mayor rapidez que la restante. Esta máquina estará desarrollando, entonces, una mayor potencia.

Definimos la potencia como la rapidez con la que un sistema efectúa un trabajo. La potencia no es estrictamente una magnitud física, sino un parámetro de ingeniería que ha resultado muy útil en el desarrollo de dispositivos tecnológicos. De hecho, el concepto de potencia surgió durante la Revolución Industrial, en la Inglaterra del siglo XVIII, como algo necesario para el desarrollo adecuado de las máquinas.

A partir de su definición, podemos ver que la potencia P resulta:

[latex]P=\frac{dW}{dt}=\vec{F}\frac{d\vec{r}}{dt}=\vec{F}\cdot\vec{V}[/latex]

Su unidad de medida es el Watt (W), tal que  [latex]1W=\frac{1J}{seg}[/latex]

3_ ENERGÍA POTENCIAL Y FUERZAS CONSERVATIVAS

Consideremos una partícula de masa m que se mueve desde el punto A hasta el punto B, tal como indica la figura. Calculemos el trabajo de la fuerza peso para este movimiento.

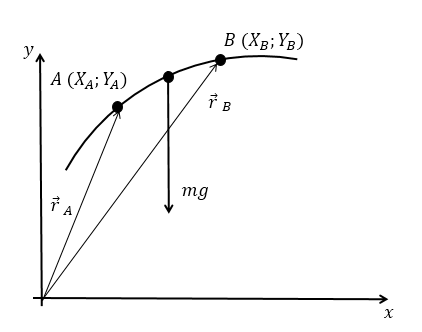
Teníamos que:

[latex]W=\int_{A}^{B}\vec{F}d\vec{r}[/latex]

Escribamos todo vectorialmente, para el sistema de coordenadas indicado en la figura:

[latex]\vec{F}=-mg\breve{j}[/latex]

[latex]d\vec{r}=dx\breve{i}+dy\breve{j}[/latex]

Por lo tanto:

[latex]W=\int_{A}^{B}\vec{F}\cdot d\vec{r}=\int_{A}^{B}-mgdx=mgy_{A}-mgy_{B}[/latex]

Vamos a analizar la expresión obtenida[1]:

• – el trabajo de la fuerza peso es independiente de la trayectoria seguida por la partícula.
• – el trabajo de la fuerza peso sí depende de los puntos inicial y final de la trayectoria.
• – sobre una trayectoria cerrada, es decir, cuando A=B, el trabajo de la fuerza peso es nulo.

Ahora, reescribamos la expresión obtenida en esta forma:

[latex]W=-(mgy_{B}-mgy_{A})[/latex]

Denominaremos energía potencial gravitatoria E_pg  al término [latex]mgy[/latex]. Notemos que la E_pg depende solamente de la posición de la partícula.

Por lo tanto, podemos escribir el trabajo de la fuerza peso como:

[latex]W_{peso}=-(E_{pg}^{B}-E_{pg}^{A})=-\Delta E_{pg}[/latex]

Las propiedades que acabamos de encontrar respecto del trabajo de la fuerza peso son consecuencia de que el peso es una fuerza conservativa. El sentido del término “conservativa” se hará claro cuando un poco más adelante veamos la relación entre el trabajo y la energía mecánica.

Definiremos una fuerza conservativa como aquella que cumple con la siguiente propiedad:

[latex]\vec{F}=-\vec{\triangledown} E_{p}[/latex]

Aquí [latex]\vec{\triangledown}[/latex] es el “operador gradiente”, un operador matemático que, aplicado a una función escalar la transforma en un vector, de acuerdo con la siguiente definición:

[latex]\vec{\triangledown} E_{p}=\left (\frac{\partial E_{p}}{\partial x};\frac{\partial E_{p}}{\partial y};\frac{\partial E_{p}}{\partial z} \right )[/latex]

Para que [latex]\vec{F}[/latex] sea una fuerza conservativa deberá tener asociada, por lo tanto, una función E_p que llamaremos energía potencial, y que debe depender sólo de la posición. Ya encontramos una energía potencial asociada con la fuerza peso; de la misma forma habrá una “energía potencial eléctrica”; “energía potencial elástica”, etc.

Notemos que, para el caso de una fuerza que dependa de una sola coordenada, el gradiente se reduce a una derivada parcial. Denominemos r a dicha coordenada, y entonces:

[latex]\vec{F}=-\frac{\partial E_{p}}{\partial r}\breve{r}[/latex]

Por lo tanto:

[latex]\int_{A}^{B}\vec{F}\cdot d\vec{r}=-\Delta E_{p}[/latex]

Es decir:

[latex]W_{F}=-\Delta E_{p}[/latex]

El resultado anterior es general, vale para toda fuerza conservativa. De aquí pueden obtenerse nuevamente las propiedades que habíamos encontrado para el trabajo de la fuerza peso, entre ellas el ser independiente de la trayectoria.

Veamos ahora distintos ejemplos de fuerzas conservativas.

4_ FUERZAS CENTRALES

Una fuerza será central cuando la energía potencial asociada con la misma dependa sólo del módulo del vector posición y no de su dirección; es decir, E_p=E_p(r) .

Las fuerzas centrales, por definición, son fuerzas conservativas. Para comprobarlo, dada una fuerza central debemos hallar su energía potencial asociada. Lo haremos en dos ejemplos de importancia física.

a) Consideremos una fuerza del tipo de la fuerza elástica, dada por F=-kr, con k una constante. Buscaremos su energía potencial asociada.

Postulamos: [latex]F=-\frac{\partial E_{p}}{\partial r}=-kr[/latex]. La idea es encontrar la E_p sin incurrir en ningún absurdo matemático.

Operando, tenemos que:

[latex]E_{p}=\int kr dr[/latex]

Integrando:

[latex]E_{p}= \frac{1}{2}kr^{2}+C[/latex]

donde fue necesario agregar la constante numérica C por tratarse de una integral indefinida. La presencia de C nos indica que, realmente, no puede calcularse la energía potencial en forma “absoluta”, sino que sólo podemos calcular la diferencia de energía potencial entre dos puntos.

Ahora bien, de todas formas puede asignarse un valor razonable para C, a partir de consideraciones físicas. Si [latex]r\rightarrow 0[/latex] asignamos para la E_p un valor nulo, dado que, pensando en términos de una fuerza elástica, correspondería a la situación de no-deformación. Por ello, podemos tomar lógicamente C = 0.

b) Sea ahora una fuerza de tipo gravitatorio, es decir [latex]F=-\frac{k}{r^{2}}[/latex]

Procediendo en la misma forma que en el caso anterior, resulta:

[latex]E_{p}=-\frac{k}{r}+C[/latex]

En este caso, para determinar C hacemos [latex]r\rightarrow \infty[/latex]. Para una distribución finita de masa, el campo gravitatorio, en módulo, debe disminuir conforme se incrementa la distancia a las masas, por lo que , y nuevamente resulta C = 0.

5_ LA ENERGÍA CINÉTICA

Consideremos el diagrama de la figura, y escribamos la Segunda Ley de Newton sobre el eje tangencial a la curva.

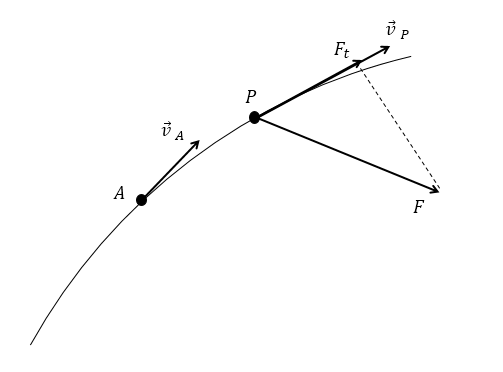
Tendremos que:

[latex]F_{t}=m\frac{dV}{dt}[/latex]

Si llamamos dS al elemento diferencial de curva correspondiente a una parte muy pequeña de la trayectoria de la partícula:

[latex]dW=F_{t}dS=m\frac{dV}{dt}dS[/latex]

Por lo tanto:

[latex]dW=mVdV[/latex]

Entonces:

[latex]W=\int_{A}^{B}F_{t}dS=\int_{A}^{B}mVdV=\frac{1}{2}mV_{B}^{2}-\frac{1}{2}mV_{A}^{2}[/latex]

Llamaremos energía cinética E_c  al término [latex]\frac{1}{2}mV^{2}[/latex].

De donde:

[latex]W=\Delta E_{c}[/latex]

Debemos tener en cuenta que aquí W es el trabajo de todas las fuerzas que actúan sobre la partícula, es decir, es el trabajo total o trabajo de la fuerza resultante. La expresión anterior se denomina Teorema de las Fuerzas Vivas, nombre que proviene de que, en el siglo XVIII, en lugar de trabajar con la energía cinética, se operaba con la denominada fuerza viva, definida como [latex]mV^{2}[/latex].

La energía cinética se asocia al movimiento de una partícula, mientras que la energía potencial lo hace con su posición.

Pregunta: ¿La energía cinética es una magnitud absoluta o relativa?

Respuesta: Relativa, porque la velocidad es relativa al sistema de referencia utilizado.

Ahora, definamos la energía mecánica o energía mecánica total de una partícula en la forma:

E_m=E_p+E_c

Previamente, habíamos encontrado que, para las fuerzas conservativas, se cumple que:

[latex]W_{fcons}=-\Delta E_{p}[/latex]

y que, para la sumatoria de todas las fuerzas, tanto conservativas como no conservativas,

[latex]W=-\Delta E_{c}[/latex]

Por lo tanto:

[latex]W_{fcons}+W_{fno-cons}=\Delta E_{c}=\Delta E_{m}-\Delta E_{p}[/latex]

Entonces:

[latex]W_{fno-cons}=\Delta E_{m}[/latex]

Por lo tanto, las fuerzas no conservativas serán aquellas cuyo trabajo genere variaciones en la energía mecánica total de una partícula. Son fuerzas no conservativas la fuerza de rozamiento, en general todas las fuerzas de contacto y muchas otras. El resultado que acabamos de obtener es el Teorema del Trabajo y la Energía Mecánica.

Un error habitual es confundir el término fuerza no conservativa con fuerza disipativa. Será disipativa, una fuerza que genere una disminución en la energía mecánica de una partícula. Pero las fuerzas no conservativas, incluyendo el rozamiento, pueden generar incrementos en la energía mecánica. ¿Cómo puede trabajo del rozamiento aumentar la energía? Supongan que sostienen un paquete con la mano. La mueven horizontalmente hacia delante, a partir del reposo. Supongamos que el paquete se mueve junto con la mano; eso es debido a la fuerza de rozamiento estático entre la mano y el paquete. Claramente, el paquete adquirió energía porque, sin modificar su energía potencial, aumentó la mecánica, y la responsable de ello fue la fuerza de rozamiento.

Si sobre una partícula el trabajo de las fuerzas no-conservativas es nulo, la energía mecánica de la partícula no se modificará. Resolvamos ahora un problema para poner en práctica los conceptos de energía y conservación.

6_ PROBLEMAS

PROBLEMA 1

Una roca de 0,50 kg de masa desliza 35m cuesta abajo por una pendiente helada, que forma un ángulo de 30° con la horizontal. El coeficiente de rozamiento dinámico es 0,01. Calcular el trabajo de cada una de las fuerzas que actúan sobre la roca y también el trabajo total.

Solución: realicemos el diagrama de cuerpo libre.

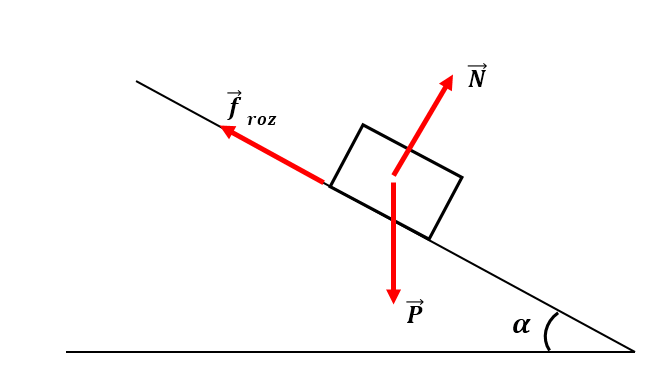
Notemos que todas las fuerzas actuantes sobre la roca son constantes, y tampoco cambia la dirección entre cada una de ellas y el desplazamiento de la roca. Por lo tanto, podemos utilizar la expresión “simplificada” para el trabajo.

El trabajo de la normal: es nulo, dado que es perpendicular al desplazamiento.

El trabajo de la fuerza peso:

[latex]W_{peso}=mg (cos 60)(15m)=36,75 J[/latex]

El trabajo de la fuerza de rozamiento dinámica:

[latex]W_{froz}=\mu_{d}mg (cos 30)(15m)(cos180)\cong -0,64 J[/latex]

El trabajo total se obtiene sumando los trabajos individuales y resulta:

[latex]W_{total}=36,11 J[/latex]

Habría que hacer una integral de línea.

PROBLEMA 2

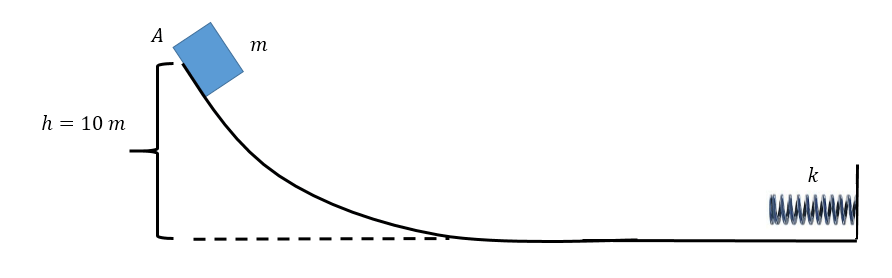
Consideremos el esquema de la figura. La masa m, de 1 kg, se deja caer desde el punto A. Recorre la curva indicada hasta comprimir el resorte, de constante k=5000 N/m.

Vamos a calcular varias cosas. Primero, suponiendo que no hay rozamiento, calculemos la compresión máxima del resorte.

Como en este caso el trabajo de las fuerzas no conservativas es nulo, tenemos que

E_mA=E_mB

siendo B el punto de máxima compresión del resorte. Por lo tanto:

[latex]mgh=\frac{1}{2}k(\Delta x) ^{2}[/latex]

y obtenemos que [latex]\left | \Delta x \right |=20cm[/latex], aproximadamente.

Es interesante ver los cambios experimentados por la energía, cuyo valor total permanece constante, pero que comienza siendo energía potencial gravitatoria, al pie de la trayectoria curva se ha transformado totalmente en energía cinética, al comprimir el resorte se transforma en energía potencial elástica y luego, si la masa se separa del resorte, vuelve a alcanzar la altura original, repitiéndose indefinidamente el ciclo.

Ahora, consideremos que sí existe rozamiento (ver figura), tal que [latex]\mu _{d}=0,27[/latex]  y d = 24m.

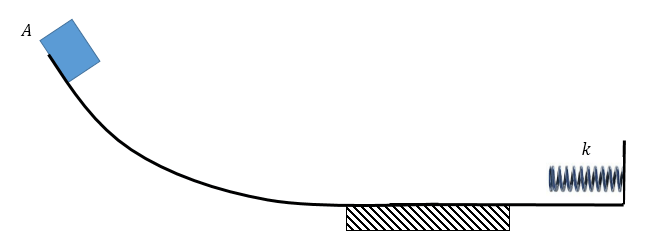
Podemos anticipar que la compresión del resorte deberá ser menor que en el caso anterior, debido a la energía que se pierde por el trabajo del rozamiento. Tendremos que:

Resolviendo, obtenemos que: , aproximadamente.

Ahora, si la masa m después de comprimir el resorte vuelve a iniciar el movimiento, alcanzará una altura inferior que la de partida. Cada vez que pase por la zona con rozamiento esa altura será menor. ¿Cómo podemos calcular cuántas veces la partícula atraviesa la zona con rozamiento hasta detenerse? Notemos que la partícula tenía inicialmente una energía igual a 98J. El trabajo del rozamiento es de -63,5J aproximadamente, que es lo que la partícula pierde en cada pasada. Efectuamos la división correspondiente y resulta: 1,54. Es decir, la partícula pasa una vez completa por la zona con rozamiento y se detiene casi a la mitad de la segunda pasada. Esto último nos permite, incluso, calcular exactamente dónde se detendrá, efectuando (24m) (0,54)=12,96m del extremo de la zona con fricción.

¿Cómo podemos calcular el trabajo de la fuerza peso desde el punto A hasta la compresión máxima del resorte? Sabemos que:

[latex]W_{peso}=-\Delta E_{pg}=mgh=98J[/latex]

¿Es casual que el trabajo del peso dio un resultado positivo?

No, porque como el trabajo del peso es independiente de la trayectoria (es una fuerza conservativa), siempre que la posición final de la partícula esté “por debajo” de la inicial, el trabajo del peso deberá ser positivo.

Ahora, calculemos el trabajo de la fuerza elástica, durante la compresión del resorte.

Pregunta: ¿Podemos utilizar la fórmula [latex]W=Fd(cos\alpha )[/latex]?

Respuesta: No, porque la fuerza elástica es una fuerza variable con la posición.

Entonces:

[latex]W_{felastica}=-\Delta E_{pe}=-\frac{1}{2}k(\Delta x)^{2}[/latex]

y tomará un valor u otro según consideremos el caso con o sin fricción. Nuevamente, el signo del trabajo resulta claro comparando la dirección del movimiento de la partícula con el sentido de la fuerza.

Numerosos problemas y situaciones físicas pueden resolverse utilizando este y otros Teoremas de Conservación, pero no debemos olvidar que tales teoremas son consecuencia de la Segunda Ley de Newton. Para verificarlo, resolvamos el siguiente problema.

PROBLEMA 3

Consideremos un casquete semiesférico, tal como muestra la figura. Supondremos que el rozamiento es despreciable. En el punto más alto del casquete hay una partícula. La misma comienza a moverse con una velocidad inicial tan pequeña que puede considerarse aproximadamente nula. Queremos calcular en qué punto de la superficie del casquete la partícula se separa del mismo.

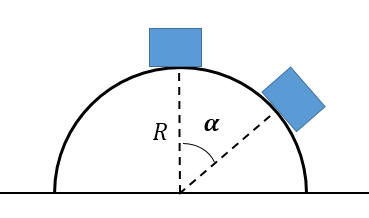
SOLUCIÓN

Vamos a resolver el problema de dos formas diferentes. Primero, utilizando sólo las Leyes de Newton; luego, nos permitiremos utilizar conceptos de energía. Y por último vamos a comparar el grado de dificultad obtenido empleando uno u otro método.

Para el sistema de coordenadas indicado, planteando la Segunda Ley de Newton en dirección radial, tenemos que:

[latex]mg (cos \alpha)-N=m\frac{V^{2}}{R}[/latex]

Como vamos a buscar en qué punto la partícula se separa del casquete, tendremos que, en dicho punto N=0, por lo que:

[latex]g (cos \alpha)=\frac{V^{2}}{R}=\omega ^{2}R[/latex]

Ahora, planteemos la ecuación en dirección tangencial:

[latex]mg (sen \alpha)=m\frac{dV}{dt}=mR\frac{d\omega }{dt}[/latex]

Tenemos que integrar esta última ecuación. No podemos hacerlo en forma directa, porque el ángulo α depende del tiempo. Por lo tanto, previamente en el miembro derecho de la ecuación multiplicamos y dividimos por dα.

[latex]g (sen \alpha)=R\frac{d\omega }{dt}\frac{d\alpha }{d\alpha }[/latex]

Pero [latex]\omega =\frac{d\alpha }{dt}[/latex], de donde:

[latex]g (sen\alpha )d\alpha =R\omega d\omega[/latex]

Integramos:

[latex]\int_{0}^{\alpha }g sen (\alpha )d\alpha =\int_{0}^{\omega }R\omega d\omega[/latex]

Resolviendo las integrales, obtenemos:

[latex]g (1-cos\alpha )=\frac{1}{2}R\omega ^{2}[/latex]

Ahora, reemplacemos en la que expresión que habíamos obtenido para la coordenada normal:

[latex]g cos\alpha=2g(1-cos\alpha )[/latex]

Finalmente, resulta:

[latex]cos\alpha=\frac{2}{3}[/latex]

El problema fue resuelto correctamente, pero ahora veamos qué ocurre si nos permitimos utilizar el Teorema del Trabajo y la Energía Mecánica. La ecuación

[latex]gcos\alpha=\omega ^{2}R[/latex]

seguirá siendo necesaria, porque ella resulta de la condición exigida por el problema, de que la partícula se separe del casquete semiesférico. Pero ahora, como el trabajo de la normal es nulo y supusimos que no había rozamiento, la energía mecánica en el punto inicial y el punto de separación es la misma, con lo cual:

[latex]mgR=\frac{1}{2}mV^{2}+mgR(cos\alpha )[/latex]

Ahora, sólo falta escribir [latex]V=\omega R[/latex], combinar ambas ecuaciones y con sólo algunos pasajes de términos llegamos al mismo resultado que con el procedimiento anterior, es decir , [latex]cos \alpha =\frac{2}{3}[/latex]

La pregunta que surge entonces lógicamente es: ¿por qué aplicando conservación de la energía la resolución del problema resultó mucho más sencilla? Empleando sólo las Leyes de Newton el problema matemático fue la necesidad de integrar la ecuación. Pero los Teoremas de Conservación realmente son integrales de la Segunda Ley de Newton, con lo que, en el procedimiento que utilizó energía, la integral estaba automáticamente resuelta. Así podemos apreciar el verdadero alcance de las leyes newtonianas, y comprender que “dinámica” y “conservación” no son dos temas separados, sino distintas aplicaciones del modelo clásico de partícula desarrollado por Newton. De hecho, el nombre original de los que hoy llamamos “Teoremas de Conservación” fue “Primeras Integrales del Movimiento”.