Índice

1. Modelo de Sistema de Partículas
2. Sistema de Referencia Laboratorio
3. Centro de Masa de un Sistema de Partículas
4. Velocidad del CM de un Sistema de Partículas
5. Aceleración del CM de un Sistema de Partículas
6. Dinámica de un Sistema de Partículas
7. Segunda Ecuación Universal para un Sistema de Partículas
8. Impulso y Cantidad de Movimiento para un Sistema de Partículas
9. Momento angular y Torque para un Sistema de Partículas
10. Trabajo y energía en un Sistema de Partículas
11. Energía Potencial Gravitatoria de un Sistema de Partículas
12. Energía cinética de un Sistema de Partículas
13. Ecuaciones Universales para la Dinámica de un SP
14. Dinámica Impulsiva para un Sistema de Partículas
15. Ecuaciones Universales de la Dinámica Impulsiva de un SP
16. Teorema de Conservación de la Cantidad de Movimiento de un SP
17. Teorema de Conservación del Momento Cinético de un SP
18. Colisiones
19. Coeficiente de restitución
20. Problemas
    

 Sistema de Partículas

1_ MODELO SISTEMA DE PARTÍCULAS

Cuando queremos analizar el movimiento de un conjunto de partículas que se mueven independientemente entre sí, el modelo de partícula o punto material utilizado hasta ahora ya no nos alcanza para predecir el comportamiento del conjunto. Ni siquiera para poder analizar su movimiento de traslación. Tendremos entonces que cambiar de modelo.

2_ SISTEMA DE REFERENCIA LABORATORIO

En todo este capítulo vamos a trabajar con dos sistemas de referencia: el sistema del laboratorio y el sistema centro de masa CM. Definimos sistema del laboratorio como un punto fijo del laboratorio que se toma como origen de un sistema de coordenadas cartesianas o polares. No se tendrán en cuenta sistemas de coordenadas rotantes.

3_ CENTRO DE MASA DE UN SISTEMA DE PARTÍCULAS

Si tenemos un conjunto de partículas (por ejemplo tres) de las cuales conocemos su posición y su masa en un instante de tiempo, vamos a definir para ese instante un punto privilegiado del espacio que, en ciertas condiciones, se comportará como si toda la masa del sistema estuviera concentrada en dicho punto. Lo denominaremos centro de masa (CM) del sistema.

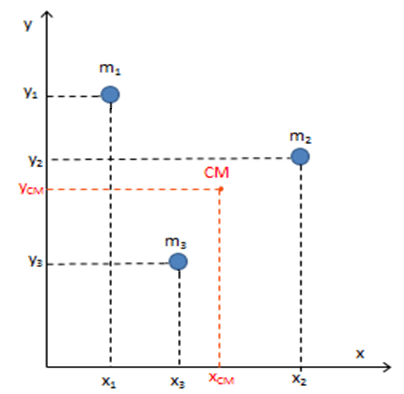
Definimos

[latex]\vec{r}_{cm}=\displaystyle\sum_{i=1}^N {\frac{\vec{r_i}m_i}{M}}[/latex]

[latex]{x}_{cm}={\frac{\displaystyle\sum_{i=1}^N {x_i}m_i}{\displaystyle\sum_{i=1}^N m_i}}[/latex]

[latex]{y}_{cm}={\frac{\displaystyle\sum_{i=1}^N {y_i}m_i}{\displaystyle\sum_{i=1}^N m_i}}[/latex]

Si deseamos encontrar el CM del sistema de partículas en el espacio también usaríamos el mismo cálculo algebraico para encontrar su componente en el eje z  sería

[latex]{z}_{cm}={\frac{\displaystyle\sum_{i=1}^N {z}_im_i}{\displaystyle\sum_{i=1}^N m_i}}[/latex]

Por otro lado las tres expresiones son las componentes del vector posición del CM. Por todo esto concluimos que, siendo M la masa total del SP, entonces el centro de masa (CM) de un sistema de partículas (SP) es la media ponderada de las posiciones de todas sus masas. Según nuestra definición aplicada a este ejemplo:

[latex]\vec{r}_{CM}=\frac{(m_{1}\vec{r}_{1}+m_{2}\vec{r}_{2}+m_{3}\vec{r}_{3})}{(m_{1}+m_{2}+m_{3})}[/latex]

Resulta entonces que si colocamos el sistema de referencia en el CM del SP, la media o promedio de las posiciones ponderadas relativas al CM del SP es nulo.

La posición relativa de cada partícula al CM es [latex]\vec{r}_{i-CM}=\vec{r}_{i}-\vec{r}_{CM}[/latex]

Luego [latex]\vec{r}_{i}=\vec{r}_{i-CM}+\vec{r}_{CM}[/latex]

Si lo reemplazamos en la fórmula del CM  resulta:

[latex]\vec{r}_{CM}M=\sum m_{i}(\vec{r}_{i-CM}-\vec{r}_{CM})[/latex]

o también

[latex]\vec{r}_{CM}M=\sum m_{i}\vec{r}_{i-CM}+\vec{r}_{CM}M[/latex]

Expresión de la cual, como habíamos afirmado, resulta

[latex]\sum m_{i}\vec{r}_{i-CM}=\vec{0}[/latex]

Este resultado será importante cuando trabajemos con el momento cinético de un sistema de partículas.

4_ VELOCIDAD DEL CM DE UN SISTEMA DE PARTÍCULAS

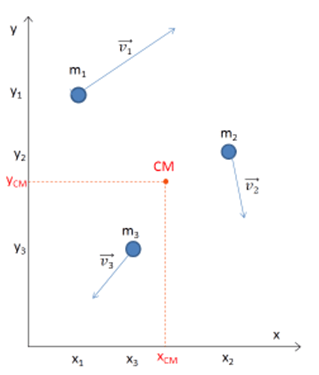
En base a la expresión de la posición del CM del SP podemos encontrar la velocidad del CM del mismo simplemente derivando la expresión anterior:

[latex]\vec{r}_{CM}=\frac{\sum m_{i}\vec{r}_{i}}{M}[/latex]

Suponiendo que la masa de cada partícula se mantiene constante y la única variable es la posición. Entonces:

[latex]\vec{v}_{CM}=\frac{\sum m_{i}\vec{v}_{i}}{M}[/latex]

En nuestro ejemplo:

[latex]\vec{v}_{CM}=\frac{(m_{1}\vec{v}_{1}+m_{2}\vec{v}_{2}+m_{3}\vec{v}_{3})}{(m_{1}+m_{2}+m_{3})}[/latex]

Análogamente al razonamiento realizado con la posición, si calculamos las velocidades relativas al CM es:

[latex]\vec{v}_{i-CM}=\vec{v}_{i}-\vec{v}_{CM}[/latex]

[latex]\vec{v}_{CM}=\frac{\sum m_{i}(\vec{v}_{i-CM}+\vec{v}_{CM})}{M}[/latex]

De todo esto resulta

[latex]\sum m_{i}\vec{v}_{i-CM}=\vec{0}[/latex]

 5_ ACELERACIÓN DEL CM DE UN SISTEMA DE PARTÍCULAS

Procediendo de modo análogo, es decir derivando con respecto al tiempo la expresión de la velocidad del CM, podemos definir

[latex]\vec{a}_{CM}=\frac{\sum m_{i}\vec{a}_{i}}{M}[/latex]

y procediendo matemáticamente de manera análoga a las precedentes obtenemos:

[latex]\sum m_{i}\vec{a}_{i-CM}=\vec{0}[/latex]

6_ DINÁMICA DE UN SISTEMA DE PARTÍCULAS

Definiremos en primer lugar las magnitudes físicas que trabajamos para una partícula o punto material desde el sistema de referencia laboratorio (SL) y, luego, encontraremos sus expresiones desde el sistema de referencia CM.

1.- Cantidad de movimiento lineal, momento lineal o momentum del CM de un SP

Así como definimos como cantidad de movimiento de una partícula [latex]\vec{p}=m\vec{v}[/latex],  la cantidad de movimiento de un SP será la suma vectorial de las cantidades de movimiento de cada una de las partículas que componen el sistema.

Vamos a simbolizar con [latex]\vec{P}_{SIST}[/latex] esta magnitud para no confundirla con la de una sola partícula  [latex]\vec{P}_{SIST}=\sum \vec{p}_{i}[/latex]; [latex]\vec{P}_{SIST}=\sum m_{i}\vec{v}_{i}[/latex].

Todas estas magnitudes están referidas al sistema laboratorio.

2.- Cantidad de movimiento angular o momento cinético o momento de la cantidad de movimiento de un SP

Para una partícula habíamos definido el momento cinético o momento angular respecto de un punto O fijo al SL como  [latex]\vec{L^{o}}=\vec{r}_{i-O}\times \vec{p}[/latex]
. Definimos ahora el momento angular o momento cinético del SP respecto de un punto O como

[latex]\vec{L^{o}}=\sum \vec{r}_{i-O}\times m_{i}\vec{v}_{i}[/latex]

Y utilizamos nuevamente la letra mayúscula para referirnos a todo el sistema de partículas estudiado.

7_ SEGUNDA ECUACIÓN UNIVERSAL PARA UN SP

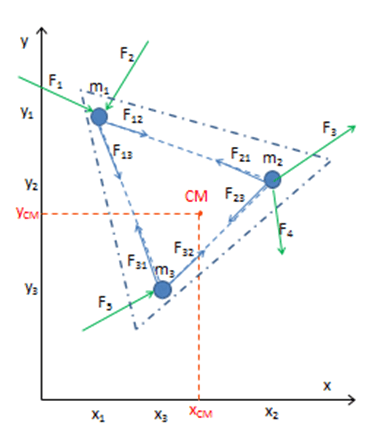
Volviendo a nuestro ejemplo de las tres partículas de masas m1, m2 y m3, hemos representado un caso hipotético en el cual dibujamos el DCL de cada partícula y en ese diagrama pusimos en evidencia todas las interacciones con el universo.

Para cada partícula del sistema podemos aplicar la segunda ley de Newton,  así para la partícula 1:

[latex]\vec{F_{1}}+\vec{F_{2}}+\vec{F_{12}}+\vec{F_{13}}=m_{1}\vec{a}_{1}[/latex]

Para la partícula 2

[latex]\vec{F_{3}}+\vec{F_{4}}+\vec{F_{21}}+\vec{F_{23}}=m_{2}\vec{a}_{2}[/latex]

Para la partícula 3

[latex]\vec{F_{5}}+\vec{F_{31}}+\vec{F_{32}}=m_{3}\vec{a}_{3}[/latex]

La expresión de la segunda ley de Newton para un SP será entonces:

[latex]\sum \vec{F_{i}}=M\vec{a}_{CM}[/latex]

Y de acuerdo a la definición de aceleración del CM

[latex]M\vec{a}_{CM}=\sum m_{i}\vec{a}_{i}[/latex]

Entonces

[latex]\sum\vec{F}_{i}=\sum m_{i}\vec{a}_{i}[/latex]

En esta expresión [latex]\sum\vec{F}_{i}[/latex]  representa todas las interacciones de todas las partículas del sistema y la aceleración es la aceleración del CM del mismo.

Sin embargo, destacamos en la figura 3 con distinto color las fuerzas de interacción entre las partículas del sistema (azules) de aquellas fuerzas que provienen de la interacción de cada partícula con el exterior (verdes). Vamos a llamar fuerzas interiores del SP a las que surgen de las interacciones entre dichas partículas (Ej. F₁₂ y F₂₁) y fuerzas exteriores a las otras.

Entonces podemos escribir la 2º ley de Newton como:

[latex]\sum\vec{F}_{i}=\sum M\vec{a}_{CM}[/latex]

[latex]\sum\vec{F}_{ext}+\sum\vec{F}_{int}=\sum M\vec{a}_{CM}[/latex]

Sin embargo, las fuerzas interiores corresponden a pares de interacción contenidos en el sistema y entonces su suma vectorial es nula [latex]\sum \vec{F}_{int}=\vec{0}[/latex]
.  Con lo que queda como expresión de la 2º ecuación universal para un SP:

[latex]\sum\vec{F}_{ext}=M\vec{a}_{CM}[/latex]

De acuerdo con esta expresión sólo las fuerzas exteriores al SP pueden acelerar el CM del sistema. Es decir, sólo las fuerzas exteriores al sistema pueden cambiar el estado de movimiento del CM del SP.

En nuestro ejemplo

[latex]\vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}+\vec{F}_{4}+\vec{F}_{5}=M\vec{a}_{CM}[/latex]

8_ IMPULSO Y CANTIDAD DE MOVIMIENTO DEL SP

Si las fuerzas actúan sobre cada partícula por un cierto intervalo de tiempo generan un impulso  [latex]\vec{J}=\int_{0}^{t}\vec{F} dt[/latex] de modo tal que la suma de todos los impulsos, aplicados a la misma, es igual a la variación de la cantidad de movimiento de la partícula.

Recordamos que para una partícula [latex]\sum \vec{J}=\vec{p}_{f}-\vec{p}_{o}[/latex] , si lo aplicamos a todo el SP [latex]\sum \vec{J_{i}}=\vec{p}_{f}-\vec{p}_{o}[/latex]
donde la sumatoria de los impulsos incluye a todos los aplicados sobre el sistema.

Pero, podemos dividir a los impulsos en interiores y exteriores al sistema. La suma de los impulsos producidos por los pares de interacción es nula, dado que los impulsos de las fuerzas de cada par se anulan mutuamente. Por esto la expresión se reduce a:

[latex]\sum \vec{J_{ext}}=\vec{p}_{f}-\vec{p}_{o}[/latex]

Nuevamente podemos afirmar que sólo los impulsos de las fuerzas exteriores pueden cambiar la cantidad de movimiento de un SP o sólo los impulsos exteriores pueden cambiar el estado de movimiento del CM de un SP.

9_MOMENTO ANGULAR Y TORQUE PARA UN SP

Consideremos un sistema formado por dos partículas, de masas m₁ y m₂ , tal como se muestra en la figura (está en el otro archivo)

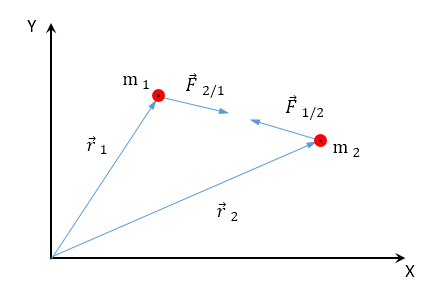
Para cada partícula se cumple individualmente el teorema de conservación del momento cinético, de donde:

[latex]\frac{d\vec{L}_{0}^{1}}{dt}=\vec{M}_{0}^{1}[/latex]

[latex]\frac{d\vec{L}_{0}^{2}}{dt}=\vec{M}_{0}^{2}[/latex]

Sumando miembro a miembro:

[latex]\frac{d\vec{L}_{sist}}{dt}=\frac{d(\vec{L}_{1}^{0}+\vec{L}_{2}^{0})}{dt}=\vec{M}_{1}^{0}+\vec{M}_{2}^{0}[/latex]

Donde:

[latex]\vec{M}_{1}^{0}=\vec{r}_{1}\times\vec{F}_{1}+\vec{r}_{1}\times\vec{F}_{2/1}[/latex]

[latex]\vec{M}_{2}^{0}=\vec{r}_{2}\times\vec{F}_{2}+\vec{r}_{2}\times\vec{F}_{1/2}[/latex]

[latex]\vec{F}_{1}[/latex]

Siendo [latex]\vec{F}_{1}[/latex] la resultante de todas las interacciones de m₁ con el exterior del sistema, y análogamente para [latex]\vec{F}_{2}[/latex] .

Ahora bien, por el Principio de Interacción: [latex]\vec{F}_{12}=-\vec{F}_{21}[/latex]

Con lo que resulta:

[latex]\frac{d\vec{L}_{sist}}{dt}=\vec{r}_{1}\times\vec{F}_{1}+\vec{r}_{2}\times\vec{F}_{2}+(\vec{r}_{2}-\vec{r}_{1})\times\vec{F}_{1/2}[/latex]

[latex]\vec{r}_{1}\times\vec{F}_{1}+\vec{r}_{2}\times\vec{F}_{2}[/latex] son los torques de las fuerzas externas al sistema.

Resta ver qué ocurre con [latex](\vec{r}_{2}-\vec{r}_{1})\times\vec{F}_{1/2}[/latex]. En los casos en que la fuerza de interacción entre las dos partículas sea colineal con el segmento que las une el producto vectorial será igual a cero. Para fuerzas como la gravitatoria o la electrostática esto es efectivamente cierto. Para fuerzas de contacto [latex]\vec{r}_{1}=\vec{r}_{2}[/latex], con lo que el término en cuestión nuevamente será nulo. Sin embargo, para fuerzas más complejas, tales como la interacción magnética, donde la fuerza es perpendicular a la velocidad de la partícula, dicho término será distinto de cero.

En lo que sigue nos limitaremos al caso de las fuerzas que estudiamos en Física I (gravitatoria, elástica, fuerzas de contacto), con lo que finalmente podemos escribir:

[latex]\frac{d\vec{L}^{0}_{sist}}{dt}=\vec{M}^{0}_{ext}[/latex]

donde [latex]\vec{M}^{0}_{ext}[/latex] es la resultante de los momentos generados por las fuerzas exteriores al sistema. Lo expresado es enteramente general para todo sistema conformado por N partículas.

10_MOMENTO ANGULAR O CINÉTICO PARA UN SP REFERIDO AL CM Y TOTAL.

Encontremos la relación que existe entre el momento cinético respecto de un punto cualquiera O fijo al laboratorio y el momento cinético respecto del CM.

La expresión general vimos que es:

[latex]\vec{L}^{0}=\sum \vec{r}_{i-o}\times m_{i}\vec{v}_{i}[/latex]

Para encontrar su relación con el momento cinético respecto del CM ( CM ) expresemos la posición y la velocidad en función del CM

[latex]\vec{r}_{i-o}=\vec{r}_{CM}+\vec{r}_{i-CM}[/latex]

y

[latex]\vec{v}_{i-o}=\vec{v}_{CM}+\vec{v}_{i-CM}[/latex]

Si reemplazamos estas dos expresiones resulta:

[latex]\vec{L}^{o}=\sum (\vec{r}_{CM}+\vec{r}_{i-CM})\times m_{i}(\vec{v}_{CM}+\vec{v}_{i-CM})[/latex]

[latex]\vec{L}^{o}=\sum \vec{r}_{CM}\times m_{i}\vec{v}_{CM}+\sum \vec{r}_{CM}\times m_{i}\vec{v}_{i-CM}+\sum \vec{r}_{i-CM}\times m_{i}\vec{v}_{CM}+\sum \vec{r}_{i-CM}\times m_{i}\vec{v}_{i-CM}[/latex]

Sacando las constantes de las sumatorias

[latex]\vec{L}^{o}=\vec{r}_{CM}\times\vec{v}_{CM}\sum m_{i}+\vec{r}_{CM}\sum m_{i}\vec{v}_{i-CM}+ \vec{v}_{CM}\sum \vec{r}_{i-CM}m_{i}+\sum \vec{r}_{i-CM}\times m_{i}\vec{v}_{i-CM}[/latex]

[latex]\vec{L}^{o}=\vec{r}_{CM}\times M\vec{v}_{CM}+\vec{r}_{CM}\times \vec{0}+\vec{v}_{CM}\times \vec{0}+\sum \vec{r}_{i-CM}\times m_{i}\vec{v}_{i-CM}[/latex]

Los términos segundo y tercero se anulan ya que [latex]\sum m_{i}\vec{v}_{i-CM}[/latex] es nulo por ser la sumatoria de las cantidades de movimiento relativas al CM y [latex]\sum m_{i}\vec{r}_{i-CM}[/latex] es la posición del CM relativo al CM que también es nulo. Luego:

[latex]\vec{L}^{o}=\vec{r}_{CM}\times M\vec{v}_{CM}+\sum \vec{r}_{i-CM}\times m_{i}\vec{v}_{i-CM}[/latex]

o sea

[latex]\vec{L}^{o}=\vec{L}^{CM}+\vec{L}^{i-CM}[/latex]

 11_ TRABAJO Y ENERGÍA EN UN SISTEMAS DE PARTÍCULAS

Para una partícula vimos que:

[latex]W_{total}=\Delta E_{c}[/latex]

ó

[latex]W_{fnc}=\Delta E_{m}[/latex]

Para un SP vimos que sólo las fuerzas exteriores producen aceleración del CM y sólo los torques de las fuerzas exteriores cambian el momento cinético del sistema. Entonces ¿será que tendremos que sumar los trabajos de las fuerzas exteriores solamente para encontrar la variación de la energía cinética del sistema? ¿Tendremos que calcular sólo los trabajos de las fuerzas no conservativas exteriores para encontrar el cambio de energía mecánica del SP?

Esto no es así. En un sistema de partículas éstas pueden moverse libremente y por esa razón sus desplazamientos no necesariamente son iguales. Si bien las fuerzas interiores correspondientes a un mismo par de interacción tienen el mismo módulo y sentidos opuestos, si difieren en sus respectivos desplazamientos entonces sus trabajos no se anulan. Por eso [latex]W_{total}[/latex] es la suma de los trabajos de todas las fuerzas actuantes tanto interiores como exteriores al sistema. [latex]W_{fnc}[/latex] es la suma de los trabajos de todas las fuerzas no conservativas, sean estas interiores o exteriores al SP.

Analicemos ahora la energía cinética y la energía potencial gravitatoria de un SP.

Para un sistema de partículas, las energías cinética y potencial se calculan respectivamente:

[latex]E_{c}=\sum \frac{1}{2}m_{i}v_{i}^{2}[/latex]  (3)

y

[latex]E_{pg}=\sum m_{i}gy_{i}[/latex]    (4)

Analicemos un poco cada una de las expresiones anteriores.

12_ ENERGÍA POTENCIAL GRAVITATORIA DE UN SP

 Si consideramos el SP cerca de la superficie terrestre la expresión (4) podemos escribirla:

[latex]E_{pg}=\sum m_{i}gy_{i}[/latex]

[latex]E_{pg}=g\sum m_{i}y_{i}[/latex]  (3)

Pero, de la definición de centro de masa

[latex]y_{CM}=\sum \frac{m_{i}y_{i}}{M}[/latex]  o sea que  [latex]M \, y_{CM}=\sum m_{i}y_{i}[/latex]

Si reemplazamos (4) en la expresion (3) nos queda [latex]E_{pg}=Mg\, y_{CM}[/latex]

Según lo hallado en (5), la energía potencial gravitatoria de un sistema de partículas es la energía potencial gravitatoria del centro de masa del sistema, como si toda la masa estuviera concentrada en ese punto.

13_ ENERGÍA CINÉTICA DE UN SP

 Luego de analizar la energía potencial gravitatoria, nos preguntamos si con la energía cinética no pasará lo mismo y podremos calcular la energía cinética del sistema como la del centro de masa.

Por esta razón trataremos de encontrar la relación entre la energía cinética de cada partícula con la energía cinética del centro de masa del sistema. Tomemos el ejemplo de tres partículas.

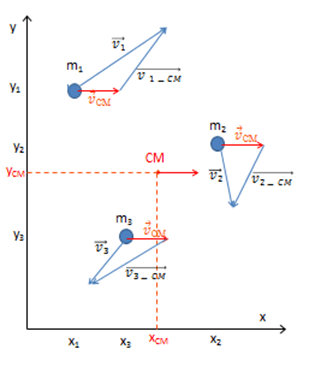
La velocidad de cada una de ellas es

[latex]\vec{v}_{i}=\vec{v}_{CM}+\vec{v}_{i-CM}[/latex]

Por lo tanto

[latex]E_{c}=\frac{1}{2}m(\vec{v}_{CM}+\vec{v}_{i-CM})^{2}[/latex]

Extrayendo de las sumatorias los factores constantes:

[latex]E_{c}=\frac{1}{2}M\vec{v}_{CM}^{2}+\vec{v}_{CM}\sum m_{i}\vec{v}_{i-CM}+\frac{1}{2}\sum m_{i}\vec{v}_{i-cm}^{2}[/latex]

Si analizamos el segundo término encontrado y recordando la definición de [latex]\sum m_{i}\vec{v}_{CM}[/latex]

[latex]\sum m_{i}\vec{v}_{i-CM}[/latex]  es la suma de las cantidades de movimiento relativas al centro de masa y como ya hemos visto es nula.

El resultado al que arribamos es entonces:

[latex]E_{c}=\frac{1}{2}M\vec{v}_{CM}^{2}+\frac{1}{2}\sum m_{i}\vec{v}_{i-cm}^{2}[/latex]

Esto significa que: la energía cinética total del sistema de partículas respecto al LAB no es igual a la energía cinética del centro de masa, sino que hay que agregarle un término. Este término es la energía cinética relativa al centro de masa.

Recordar entonces que:

[latex]E_{c}=\frac{1}{2}\sum m_{i}\vec{v}^{2}_{i}\neq \frac{1}{2}M\vec{v}_{CM}^{2}[/latex]

Analicemos un poco más el término de la energía cinética relativa al centro de masa. Cada una de las velocidades relativas vi-CM puede a su vez descomponerse en una dirección radial (dirección que une el punto material con el CM) y una dirección perpendicular a la anterior que hemos llamado transversal tal como se muestra en la figura.

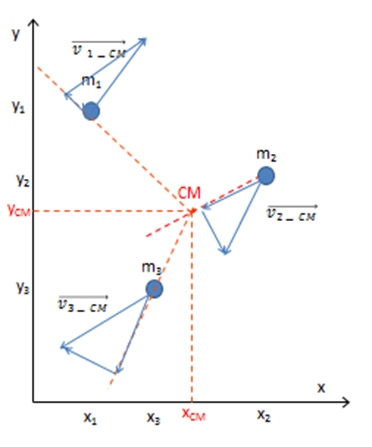
[latex]\vec{v}_{i-CM}=\vec{v}_{ir}+\vec{v}_{itr}[/latex] donde [latex]\vec{v}_{ir}[/latex] son las componentes de la velocidad relativa al CM radiales o en la dirección que une la partícula con el CM del sistema y  [latex]\vec{v}_{itr}[/latex] son las componentes de la velocidad relativa al CM de cada partícula en la dirección transversal.

Luego  [latex]E_{c}=\frac{1}{2}Mv_{CM}^{2}+\frac{1}{2}\sum m_{i}(\vec{v}_{ir}+\vec{v}_{itr})^{2}[/latex]

Nuevamente deberíamos desarrollar el binomio, pero como los vectores son perpendiculares, su producto escalar es nulo.

La energía cinética de un sistema de partículas queda entonces conformada por tres términos

[latex]E_{c}=\frac{1}{2}Mv_{CM}^{2}+\frac{1}{2}\sum m_{i}\vec{v}_{ir}^{2}+\frac{1}{2}\sum m_{i}\vec{v}_{itr}^{2}[/latex]

La energía cinética que tiene el sistema si toda la masa se concentrara en su CM es [latex]E_{c}=\frac{1}{2}Mv_{CM}^{2}[/latex]  (energía cinética de traslación).

La energía cinética de expansión o compresión de efectos de deformación del sistema  (las partículas se alejan del CM = expansión o se acercan al CM = compresión) y la energía cinética que tienen las partículas por rotar alrededor del CM  energía cinética de rotación respecto al CM (que tiene también efectos de deformación ya que no rotan todas con la misma velocidad angular instantánea, ni siquiera rotan todas en el mismo sentido).

14_ ECUACIONES UNIVERSALES DE LA DINÁMICA DE UN SP

Primera Ecuación Universal     

[latex]\sum \vec{F}_{ext}=\frac{d\vec{P}}{dt}[/latex]

Segunda Ecuación Universal     

[latex]\sum \vec{r}_{i-o}\times \vec{F}_{ext}=\frac{d\vec{L}^{o}}{dt}[/latex]

Ecuación del Trabajo y la Energía

[latex]W_{fnc}=\bigtriangleup E_{c}+\bigtriangleup E_{p}[/latex]

Estas ecuaciones o sus enunciados como teoremas de conservación constituyen el modelo físico-matemático que nos permite encontrar soluciones a los problemas sobre SP.

15_ DINÁMICA IMPULSIVA DEL SP

De todo lo desarrollado se desprenden otras ecuaciones que podemos aplicar y que abren un nuevo capítulo para el abordaje de problemas de SP denominado dinámica impulsiva.

De la misma manera que encontramos el impulso integrando en el tiempo la fuerza aplicada a una partícula, podemos integrar en el tiempo el torque aplicado al SP. Ya vimos que:

[latex]\sum \vec{r}_{i-o}\times \vec{F}_{ext}=\frac{d\vec{L}^{o}}{dt}[/latex]

Integrando esta expresión nos queda:

[latex]\sum \vec{r}_{i-o}\times \int_{0}^{t}\vec{F}_{ext}\, dt=\int_{0}^{t}\frac{d\vec{L}^{o}}{dt} dt[/latex]

o sea

[latex]\sum \vec{r}_{i-o}\times \vec{J}_{ext}=\bigtriangleup \vec{L}^{o}[/latex]

Donde [latex]\vec{r}\times \vec{J}[/latex] se denomina impulso angular

La expresión anterior se lee: La suma de los impulsos angulares de todas las fuerzas exteriores actuantes en un SP, respecto a un punto, es igual al cambio de momento cinético respecto a ese mismo punto.

16_ ECUACIONES UNIVERSALES DE LA DINÁMICA IMPULSIVA DE UN SP

1.- Ecuación de traslación  

[latex]\sum \vec{J}_{ext}=\vec{P}_{f}-\vec{P}_{i}[/latex]

2.- Ecuación de rotación

[latex]\sum \vec{r}_{i-o}\times \vec{J}_{ext}=\bigtriangleup \vec{L}^{o}[/latex]

Este conjunto de ecuaciones permite utilizar caminos alternativos de resolución de problemas de sistemas de partículas, que nos permiten a veces encontrar velocidades cuando no se conocen las aceleraciones de todas las partículas integrantes del sistema en estudio.

17_ TEOREMA DE CONSERVACIÓN DE LA CANTIDAD DE MOVIMIENTO DE UN SP

La primera ecuación universal de la dinámica impulsiva de un SP es una ecuación de balance.

[latex]\sum \vec{J}_{ext}=\vec{P}_{f}-\vec{P}_{i}[/latex]

Es decir, nos relaciona el valor de la cantidad de movimiento del sistema en dos instantes de tiempo. Cada vez que tenemos una ecuación de balance, asociada a la misma hay un teorema de conservación. En este caso la variación de la cantidad de movimiento tiene asociada el teorema de conservación de la cantidad de movimiento que se enuncia:

Si la sumatoria de los impulsos de las fuerzas exteriores al SP es nula, entonces se conserva la cantidad de movimiento del sistema.

Si [latex]\sum \vec{J}_{ext}=\vec{0}[/latex] entonces ⇒ [latex]\vec{P}_{SIST}=cte[/latex]

Analicemos todos los casos en los que se va a cumplir este teorema.

1º Si no existen fuerzas exteriores al sistema. Es decir, el SP se encuentra aislado.

2º Si las fuerzas exteriores están en equilibrio. Es decir [latex]\sum \vec{F}_{ext}=\vec{0}[/latex].  Por la ley de inercia, el cuerpo está quieto o se mueve con movimiento uniforme y rectilíneo.

3º Si la fuerza exterior neta en una dirección es nula, se conserva la cantidad de movimiento del SP en esa dirección. Un ejemplo muy sencillo de este caso es el tiro oblicuo, se conserva [latex]\vec{P}[/latex] en la dirección horizontal.

4º En las colisiones que cumplan las siguientes condiciones. Si la fuerza exterior es contante [latex]\vec{J}_{ext}=\int_{0}^{t}\vec{F}_{NETA}dt[/latex] entonces

[latex]\vec{J}_{ext}=\vec{F}_{NETA}\int_{0}^{t}dt[/latex]

[latex]\vec{J}_{ext}=\vec{F}_{NETA}\Delta t[/latex]

Si [latex]\Delta t\rightarrow 0[/latex] entonces [latex]\vec{J}_{ext}=\vec{0}[/latex].

En los choques, los impulsos de las fuerzas exteriores constantes o acotadas son nulos (despreciables). Por ejemplo, el caso del impulso de la fuerza gravitatoria para una granada que explota en el aire.

Para analizar la conservación de una magnitud física debe utilizarse el teorema de conservación correspondiente y no consideraciones de tipo cinemático (por ej. velocidad constante o variable).

18_ TEOREMA DE CONSERVACIÓN DEL MOMENTO CINÉTICO ( ) DE UN SP

Consideremos un sistema formado por dos partículas, de masas m₁ y m₂, tal como se muestra en la figura

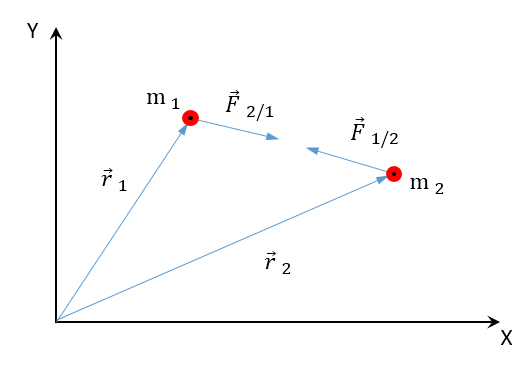
Para cada partícula se cumple individualmente el teorema de conservación del momento cinético, de donde:

[latex]\frac{d\vec{L}_{1}^{0}}{dt}=\vec{M}_{1}^{0}[/latex]

[latex]\frac{d\vec{L}_{2}^{0}}{dt}=\vec{M}_{2}^{0}[/latex]

Sumando miembro a miembro:

[latex]\frac{d\vec{L}_{sist}}{dt}=\frac{d(\vec{L}_{1}^{0}+\vec{L}_{2}^{0})}{dt}=\vec{M}_{1}^{0}+\vec{M}_{2}^{0}[/latex]

Donde:

[latex]\vec{M}_{1}^{0}=\vec{r}_{1}\times\vec{F}_{1}+\vec{r}_{1}\times\vec{F}_{2/1}[/latex]

[latex]\vec{M}_{2}^{0}=\vec{r}_{2}\times\vec{F}_{2}+\vec{r}_{2}\times\vec{F}_{1/2}[/latex]

Siendo [latex]\vec{F}_{1}[/latex]  la resultante de todas las interacciones de m1 con el exterior del sistema, y análogamente para [latex]\vec{F}_{2}[/latex].

Ahora bien, por el Principio de Interacción:

[latex]\vec{F}_{1/2}=-\vec{F}_{2/1}[/latex]

Con lo que resulta:

[latex]\frac{d\vec{L}_{sist}}{dt}=\vec{r}_{1}\times\vec{F}_{1}+\vec{r}_{2}\times\vec{F}_{2}+(\vec{r}_{2}-\vec{r}_{1})\times\vec{F}_{1/2}[/latex]

[latex]\vec{r}_{1}\times\vec{F}_{1}+\vec{r}_{2}\times\vec{F}_{2}[/latex] son los torques de las fuerzas externas al sistema.

Resta ver qué ocurre con [latex](\vec{r}_{2}-\vec{r}_{1})\times\vec{F}_{1/2}[/latex]. En los casos en que la fuerza de interacción entre las dos partículas sea colineal con el segmento que las une el producto vectorial será igual a cero. Para fuerzas como la gravitatoria o la electrostática esto es efectivamente cierto. Para fuerzas de contacto [latex]\vec{r}_{1}=\vec{r}_{2}[/latex], con lo que el término en cuestión nuevamente será nulo. Sin embargo, para fuerzas más complejas, tales como la interacción magnética, donde la fuerza es perpendicular a la velocidad de la partícula, dicho término será distinto de cero.

En lo que sigue nos limitaremos al caso de las fuerzas que estudiamos en Física I (gravitatoria, elástica, fuerzas de contacto), con lo que finalmente podemos escribir:

[latex]\frac{d\vec{L}_{sist}^{0}}{dt}=\vec{M}_{ext}^{0}[/latex]

Donde [latex]\vec{M}_{ext}^{0}[/latex]  es la resultante de los momentos generados por las fuerzas exteriores al sistema. La sumatoria de los torques producidos en el sistema por las fuerzas interiores se anulan. Sólo los torques de las fuerzas exteriores al SP pueden cambiar el momento cinético del mismo dentro de nuestra hipótesis.

Lo expresado es enteramente general para todo sistema conformado por N partículas.

 1.-MOVIMIENTO RECTILÍNEO UNIFORME

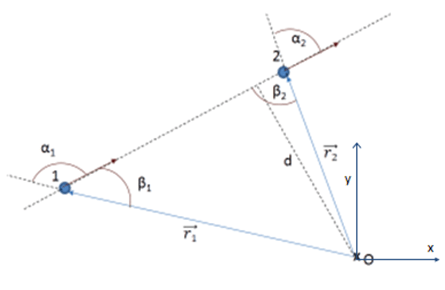
Supongamos una partícula de masa m que se mueve a lo largo de una recta con velocidad constante. En un instan t₁ se encuentra en el punto 1 y en un instante posterior t₂ se encuentra en el punto 2. Si queremos calcular el [latex]\vec{L}_{1}^{0}[/latex] y el [latex]\vec{L}_{1}^{0}[/latex] será

[latex]\vec{L}_{1}^{0}=\vec{r}_{1}\times \vec{p}[/latex]

[latex]\vec{L}_{2}^{0}=\vec{r}_{2}\times \vec{p}[/latex]

Si colocamos el sistema de referencia en O y un sistema de coordenadas ortogonales tradicional, el resultado en cada caso es:

[latex]\vec{L}_{1}^{0}=-p\, r_{1}\, sen \alpha _{1}\breve{k}[/latex]

[latex]\vec{L}_{2}^{0}=-p\, r_{2}\, sen \alpha _{2}\breve{k}[/latex]

Como  [latex]sen \, \alpha _{1}=sen \, \beta_{1}[/latex] y [latex]sen \, \alpha _{2}=sen \, \beta_{2}[/latex] por ser ángulos suplementarios y

[latex]r_{1}\, sen \, \beta_{1}=r_{2}\, sen \, \beta_{2}=d[/latex]

d: pie de la perpendicular a la recta de la trayectoria que pasa por O

Resulta:

[latex]\vec{L}_{1}^{0}=\vec{L}_{2}^{0}=-d\, p\, \breve{k}[/latex]

El momento cinético permanece constante.

2.- MOVIMIENTO CON UNA FUERZA CENTRAL

Este caso de conservación del momento cinético es muy utilizado en los movimientos planetarios.

El caso más cercano para nosotros es el de la Tierra. Veamos entonces a qué conclusiones arribamos si tomamos como sistema la Tierra en su movimiento orbital alrededor del Sol. En este caso la única fuerza actuante sobre el planeta es la fuerza de atracción gravitatoria entre el Sol y la Tierra.

Como esa interacción surge de utilizar el modelo de partícula para la Tierra y el Sol, la fuerza de atracción gravitatoria tiene una recta de acción que siempre pasa por el Sol. La Tierra realiza una órbita elíptica alrededor del Sol con éste ubicado en uno de sus focos como muestra la figura.

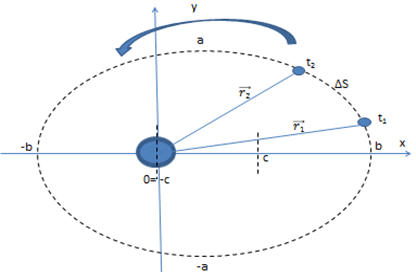
De acuerdo al teorema de conservación del momento cinético:

[latex]\vec{L}_{1}^{0}=\vec{L}_{2}^{0}=\vec{L}_{prom}^{0}[/latex]

El último término es el [latex]\vec{L}^{0}[/latex] de un punto intermedio del intervalo entre 1 y 2.  En ese punto intermedio el módulo de la velocidad la consideramos una velocidad promedio y el módulo de  la posición también será el promedio. [1]

19_ COLISIONES

Consideremos un sistema formado por dos partículas, de masas m1 y m2, que se mueven inicialmente con velocidades [latex]\vec{V}_{1}^{0}[/latex] y [latex]\vec{V}_{2}^{0}[/latex]
respectivamente. Supongamos que las partículas realizan un choque unidimensional, y que nos encontramos dentro de las hipótesis de conservación de la cantidad de movimiento del sistema, es decir, suponemos que el sistema se encuentra aislado o bien que el impulso de las fuerzas exteriores durante la colisión es despreciable.

Llamaremos [latex]\vec{V}_{1}^{f}[/latex] y [latex]\vec{V}_{2}^{f}[/latex] a las velocidades de las partículas después de la colisión.

Por lo tanto, se cumple que:

[latex]m_{1}\vec{V}_{1}^{0}+m_{2}\vec{V}_{2}^{0}=m_{1}\vec{V}_{1}^{f}+m_{2}\vec{V}_{2}^{f}[/latex]

La variación de energía cinética[latex]\Delta E[/latex] es:

[latex]\Delta E=\frac{1}{2}m_{1}(\vec{V}_{1}^{f})^{2}+\frac{1}{2}m_{2}(\vec{V}_{2}^{f})^{2}-\left [\frac{1}{2}m_{1}(\vec{V}_{1}^{0})^{2}+\frac{1}{2}m_{2}(\vec{V}_{2}^{0})^{2} \right ][/latex]

Combinando ambas ecuaciones se obtiene:

[latex]\Delta E=\frac{1}{2}\frac{m_{1}\, m_{2}}{m_{1}+m_{2}}\left [ (\vec{V}_{2}^{f}-\vec{V}_{1}^{f})^{2}-(\vec{V}_{2}^{0}-\vec{V}_{1}^{0})^{2} \right ][/latex]

Notemos que la diferencia de velocidades es la velocidad relativa de una partícula respecto de la otra, que indicaremos con el subíndice r. Por lo tanto:

[latex]\Delta E=\frac{1}{2}\frac{m_{1}\, m_{2}}{m_{1}+m_{2}}\left [ (\vec{V}_{r}^{f})^{2}-(\vec{V}_{r}^{0})^{2} \right ][/latex]

Ahora, vamos a graficar  en función de la velocidad relativa de las partículas después de la colisión. Tratándose de una expresión cuadrática el gráfico es una parábola, tal como se muestra en la figura 9.

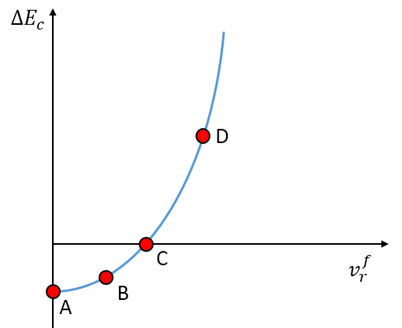
Analicemos qué ocurre en los puntos de la parábola marcados A, B, C y D.

Punto A

Aquí [latex]\vec{V}_{r}^{f}=\vec{0}[/latex]. Por lo tanto, después de la colisión las partículas quedan con la misma velocidad (están “pegadas”). Corresponde, entonces, a un choque perfectamente inelástico o choque plástico.

Podemos advertir que aquí [latex]\Delta E<0[/latex], con lo que el sistema pierde energía como consecuencia de la colisión, y además tal pérdida es la máxima posible.

Punto B

El punto B es cualquier punto ubicado entre A y C. Nuevamente, es [latex]\Delta E<0[/latex]; pero [latex]\vec{V}_{r}^{f}\neq 0[/latex].

Es un choque inelástico, en el que se sigue perdiendo energía cinética por sonido, calor u otros procesos, pero en una cantidad menor que en el punto A.

Punto C

Aquí es [latex]\Delta E=0[/latex], es decir, se conserva la energía cinética del sistema durante la colisión. Por lo tanto, [latex](\vec{V}_{r}^{f})^{2}=(\vec{V}_{r}^{o})^{2}[/latex] , es decir, [latex]\left |\vec{V}_{r}^{f} \right |=\left |\vec{V}_{r}^{o} \right |[/latex] por lo que concluimos que tampoco se modifica, en módulo, la velocidad relativa entre ambas partículas. Se trata de un choque perfectamente elástico.

Pregunta: ¿Podríamos decir que de la igualdad de módulos entre las velocidades relativas se desprende que [latex]\vec{V}_{r}^{f} =\pm \vec{V}_{r}^{o}[/latex]?

Sugerencia: pensar que no es posible que una partícula “penetre” a la otra y ver entonces que [latex]\vec{V}_{r}^{f} =-\vec{V}_{r}^{o}[/latex].

Punto D

Esta zona se denomina de los “choques explosivos” por abuso de vocabulario, porque realmente corresponde a explosiones y no a colisiones. En ellos  por lo que el proceso de interacción le entrega energía al sistema.

COLISIONES O CHOQUES MECÁNICOS

En física se acostumbra a denominar choque al intervalo de tiempo en el cual se manifiestan cambios en las velocidades de las partículas debidas a una interacción entre las mismas.

Si dos partículas que se desplazan a velocidad constante (en equilibrio dinámico) chocan entre sí, como en la dirección del choque no actúan sobre ellas impulsos o fuerzas exteriores, se conserva la cantidad de movimiento o momentum del sistema (ver Teorema de Conservación de P). Es por esto que una ecuación que nos va a permitir encontrar respuestas a situaciones en las cuales se produzca un choque es [latex]\vec{P}_{i}=\vec{P}_{f}[/latex].

Con sólo esta ecuación vamos a poder resolver los choques en los cuales los dos cuerpos que intervienen quedan unidos después del impacto. Para este caso escribimos [latex]\vec{p}_{1}+\vec{p}_{2}=(m_{1}+m_{2})\vec{v}_{f}[/latex].

En esta expresión  [latex]\vec{p}_{1}[/latex] y [latex]\vec{p}_{2}[/latex] son las cantidades de movimiento de cada una de las partículas que chocan y [latex]\vec{v}_{f}[/latex] la velocidad que tienen después del choque cuando siguen unidas. A este tipo de choque se lo denomina perfectamente inelástico o plástico.

Otro tipo de choque que se puede resolver es el caso casi teórico llamado choque elástico. En este choque suponemos que los cuerpos después de chocar adquieren exactamente la forma que tenían antes del choque. Si esto es así, no hay pérdida de energía mecánica por deformación, calor o sonido. Por esta razón además de la conservación de la cantidad de movimiento podemos plantear la conservación de la energía cinética.

1) [latex]\vec{P}_{i}=\vec{P}_{f}[/latex]

2)  [latex]\sum E_{ci}=\sum E_{cf}[/latex]

o sea [latex]m_{1i}\, \vec{v}_{1i}+m_{2i}\, \vec{v}_{2i}=m_{1f}\, \vec{v}_{1f}+m_{2f}\, \vec{v}_{2f}[/latex]
y [latex]\frac{1}{2}m_{1}\, {v}_{1i}^{2}+\frac{1}{2}m_{2}\, {v}_{2i}^{2}=\frac{1}{2}m_{1}\, {v}_{1f}^{2}+\frac{1}{2}m_{2}\, {v}_{2f}^{2}[/latex]

Con estas expresiones podemos conocer las velocidades finales de las partículas que chocan. Lo logramos si el choque es central. Entendiendo por choque central cuando las dos partículas se mueven a lo largo de la misma recta de acción. Es decir, cuando sus centros están alineados con sus velocidades. De lo contrario necesitamos un dato adicional, como por ejemplo la dirección del movimiento de una de ellas después del choque.

Pero en la gran mayoría de los choques “reales”, llamados choques inelásticos, los cuerpos luego del choque se separan y quedan deformados. Esto significa que en mayor o menor grado se pierde energía mecánica por deformación, que se llama energía potencial de deformación. Esta energía perdida sería máxima en los choques perfectamente inelásticos o plásticos.

Para poder resolver los problemas de choques inelásticos tenemos que observarlos con mayor detalle mientras interactúan. Como si los fotografiáramos en una seriada con una cámara ultra rápida.

Si hacemos esto veríamos que ambos cuerpos apenas cambian o no cambian su posición, pero se van deformando y modificando su estado de movimiento (su velocidad).

También se puede observar que salvo en el caso en el cual inicialmente ambos cuerpos tienen cantidades de movimiento opuestas e iguales (velocidad del CM nula) en todo el intervalo de contacto siempre uno de los cuerpos se está moviendo. Esto indica que durante el choque se sigue conservando la cantidad de movimiento del sistema.

Si miramos los comportamientos de los cuerpos que chocan, vemos que en el punto de contacto hay una superficie tangente a dicho punto y perpendicular a la superficie estará la dirección del impacto. Veamos algunos ejemplos

Se denomina coeficiente de restitución al número que vincula la velocidad relativa de P en la dirección del impacto en el intervalo de recuperación respecto de la velocidad relativa del intervalo de deformación en esa dirección.

[latex]e=\frac{v_{fax}-v_{fbx}}{v_{ibx}-v_{iax}}[/latex]

Note que las velocidades relativas cambian el signo cuando se miden a la derecha o a la izquierda del punto P. Por otro lado, el subíndice x significa la proyección de la velocidad en el eje x en el numerador después del choque y en el denominador antes del mismo.

20_ COEFICIENTE DE RESTITUCIÓN

Existen distintas formas de definir el coeficiente de restitución, el que da una idea de la energía cinética perdida por un sistema durante una colisión.

Aquí lo definiremos como:

[latex]e=-\frac{V_{r}^{f}}{V_{r}^{o}}[/latex]

Por lo tanto, resulta:

Para el punto A (choque plástico): [latex]e=0[/latex]

Para el punto C (choque elástico): [latex]e=1[/latex]

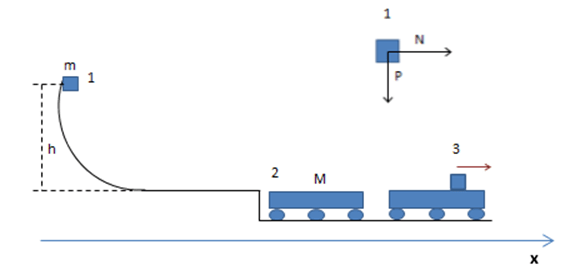
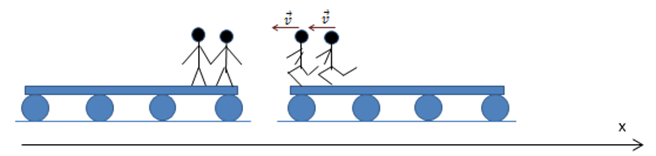
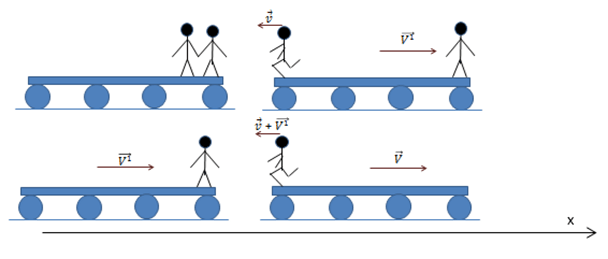
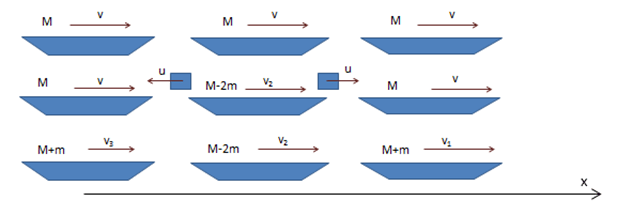
Para el punto B (choque inelástico): [latex]0

No se define el coeficiente de restitución para una explosión, dado que si la partícula que explota estaba originalmente quieta, estaríamos dividiendo por cero.

21_ PROBLEMAS

1.- Supongamos una partícula de masa m = 2 Kg que se desplaza sobre una vía curva como la que se indica en la figura partiendo del reposo desde una altura h = 2m. Al final de la rampa se “monta” sobre un carrito de masa M = 4Kg.

Después de un cierto tiempo ambos cuerpos se mueven juntos. Si el rozamiento del carrito con el piso es despreciable y el rozamiento entre la partícula y el carrito tiene un coeficiente μd = 0.4 encontrar:

1. a) La velocidad alcanzada por el sistema partícula-carrito.
2. b) El trabajo total de la fuerza de rozamiento
3. c) El desplazamiento de la partícula sobre el carrito.

Como la expresión se monta sobre el carrito da a entender que no se produce un choque y el esquema indica que el carrito tiene exactamente la misma altura de la vía, asumimos que no se pierde energía mecánica en el instante del encuentro carrito partícula. A partir de ese instante actúan dos fuerzas de rozamiento dinámico porque la partícula se mueve con mayor velocidad que el carrito hasta que se mueven juntos. Este par de fuerzas de rozamiento frena a la partícula y acelera al carrito hasta que ambos alcanzan la misma velocidad.

Para encontrar la velocidad final del sistema necesitamos calcular la velocidad con la cual la partícula se monta sobre el carrito. Como la pista curva tiene rozamiento despreciable, las únicas fuerzas que actúan entre el instante inicial y el momento en que la partícula se monta sobre el carrito son el peso y la reacción normal de la vía. En el instante 1 el DCL es el indicado.

El peso es una fuerza conservativa y la reacción de la vía se mantiene perpendicular al desplazamiento con lo cual su trabajo es nulo.

Partimos de la expresión del trabajo y la energía: [latex]W_{fnc}=\bigtriangleup E[/latex]

Como  se conserva la energía mecánica entre los instantes 1 y 2

[latex]E_{1}=E_{2}[/latex]

[latex]mgh=\frac{1}{2}mv_{2}^{2}[/latex]

Entonces:

[latex]v_{2}=\sqrt{2gh}[/latex]

[latex]\vec{v}_{2}=6,3 \frac{m}{s} \breve{i}[/latex]

Para encontrar la velocidad en el instante 3 es decir la velocidad final estudiemos el intervalo entre 2 y 3.

Entre 2 y 3, si tomamos como SP al carrito y la partícula de masa m y aplicamos las ecuaciones de la dinámica impulsiva, en el eje x no hay impulsos exteriores al sistema. En el eje x se conserva la cantidad de movimiento.

[latex]x)\, P_{ix}=P_{fx}[/latex]

[latex]x)\, mv_{2x}=(m+M)v_{f}[/latex]

De esta expresión:

[latex]\vec{v}_{f}=\frac{m}{(m+M)}\sqrt{2gh}\, \, \breve{i}[/latex]

El análisis de las magnitudes en el resultado es correcto   y el resultado numérico es:

[latex]\vec{v}_{f}=2,1 \frac{m}{s}\, \breve{i}[/latex]   Resultado de a).

Si bien la fuerza de rozamiento es dinámica (constante e igual a ) y entre 2 y 3 la  es igual a , no podemos hallar la integral del trabajo de la fuerza de rozamiento porque estaríamos sobre el carrito y este sería un SRNI y además no conocemos el desplazamiento sobre el carrito, pero, siendo las dos fuerzas de rozamiento las únicas fuerzas no conservativas que producen trabajo entre 2 y 3 podemos aplicar la ecuación del trabajo y la energía [latex]W_{fnc}=\bigtriangleup E[/latex]

En este caso:

[latex]W_{Total\, fr}=E_{cf}-E_{ci}[/latex]

[latex]W_{Total\, fr}=\frac{1}{2}(m+M)v_{f}^{2}-\frac{1}{2}mv_{2}^{2}[/latex]

[latex]W_{Total\, fr}= 6,3 J\, -\, 39,69J[/latex]

[latex]W_{Total\, fr}= -\, 33,4J[/latex]  Resultado de b)

El resultado anterior es el trabajo realizado por las dos fuerzas de rozamiento (par interacción), la que está aplicada a la partícula y la que está aplicada al carrito.

Ambos trabajos son negativos e iguales. El trabajo realizado sobre la partícula es el resultado de una fuerza de rozamiento frenante (hacia la izquierda) y un desplazamiento del carrito relativo a la partícula hacia la derecha. En este caso, siendo las fuerzas constantes:

[latex]W_{fr}= -\mu _{d}\, m\, g\, d[/latex]

[latex]d=\frac{W_{fr}}{\mu _{d}\, m\, g\, d}[/latex]

[latex]d=\frac{16,7 J}{0,4 (20N)}[/latex]

[latex]d=2,09m[/latex]

(El carrito deberá tener más de 2m de largo para que esto ocurra)

2.- Parados en el extremo derecho de un vagón de ferrocarril de masa M, se encuentran dos hombres de masa m cada uno. Todo el conjunto se encuentra en reposo. De pronto ambos corren hacia el extremo izquierdo del vagón alcanzando una velocidad [latex]\vec{v}[/latex]cada uno relativa al vagón. Llegados al extremo del vagón saltan hacia la izquierda:

1. a) los dos juntos.
2. b) primero uno y después el otro.

¿Cuál es la velocidad alcanzada en cada caso por el vagón? ¿Será la misma?

Aplicando los conocimientos de la dinámica impulsiva del SP podemos afirmar que en la dirección horizontal al sistema, formado por los dos hombres y la plataforma, no hay impulsos exteriores. Por lo tanto, se conserva la cantidad de movimiento del sistema en el eje x.

Si los dos hombres saltan juntos como [latex]P_{ix}=P_{fx}[/latex]

[latex]0=-2mv+MV[/latex]

Donde [latex]V[/latex] es la velocidad final del vagón.   [latex]V=\frac{2mv}{M}[/latex]  ó [latex]\vec{V}=\frac{2mv}{M}\, \breve{i}[/latex]

Respuesta a).

En el segundo caso tenemos dos pasos. Un primer paso en el cual salta uno de los hombres con velocidad relativa a vagón  .

Aplicando la conservación de la cantidad de movimiento en la dirección horizontal

[latex]0=-mv+(m+M)V_{1}[/latex]

Siendo [latex]V_{1}[/latex] la velocidad del hombre que queda y la del vagón.

[latex]V_{1}=\frac{m}{m+M}v[/latex]

En el segundo paso tenemos redefinimos el sistema de forma tal que el primer hombre no forme parte del mismo. La velocidad del CM ahora no es cero y la velocidad del hombre relativa a Tierra es [latex]v-V_{1}[/latex] siendo v la velocidad del hombre relativa al vagón.

[latex](m+M)V_{1}=-m(v-V_{1})+MV[/latex]

En el segundo caso, cuando saltan separadamente, la conservación de la cantidad de movimiento es:

[latex](m+M)V_{1}=-m(v-V_{1})+MV[/latex]

En esta expresión V es la velocidad final del vagón:

[latex]MV=\frac{(m+M)m}{(m+M)}\, v\, +m(v-\frac{m}{(m+M)}v)[/latex]

Operando:

[latex]MV=mv+mv-\frac{m^{2}}{m+M}v[/latex]

[latex]MV=2mv-\frac{m^{2}}{m+M}v[/latex]

[latex]MV=\frac{(2m^{2}+2mM-m^{2})}{(m+M)}v[/latex]

[latex]V=\frac{(2m^{2}+2mM-m^{2})}{(m+M)M}v[/latex]

[latex]V=\frac{mv}{M}\frac{(m+2M)}{(m+M)}[/latex]

Si comparamos esta expresión con la encontrada en a) vemos que como el corchete es mayor que 1 pero menor que 2, la velocidad final del vagón es inferior a la que alcanza en el 1º caso. Esto es así porque en realidad la velocidad del 2º hombre respecto a Tierra cuando salta es menor que en el primer caso.

¿Cómo cambia el resultado si la velocidad del 2º hombre fuera la misma respecto a Tierra?

[latex](m+M)V_{1}=-mv+MV[/latex]

[latex]MV=\frac{(m+M)}{(m+M)}mv+mv[/latex]

[latex]MV=2mv[/latex]

[latex]V=\frac{2mv}{M}[/latex]

el resultado sería el mismo que si saltan juntos. Pero, en realidad relativa a la plataforma, su velocidad en el segundo caso es mayor que en el 1º en el factor

[latex]\frac{m}{(m+M)}v[/latex]

3.- Caso de los tres botes. En un río con agua en calma avanzan a velocidad constante  tres botes de idéntica masa M. En determinado instante, desde el bote que avanza en el medio se arrojan dos paquetes idénticos de masa m al tercer bote y al primero con velocidades relativas respecto al segundo bote iguales en módulo u como indica la figura. Encontrar las velocidades alcanzadas por los tres botes.

Al bote que va en primer lugar lo llamaremos bote 1 y a los otros 2 y 3 respectivamente.

Nuevamente aplicaremos la conservación de la cantidad de movimiento del CM del sistema en la dirección horizontal. Si tomamos como sistema de partículas los tres botes con sus cargas no podemos encontrar las velocidades de cada bote. Por esta razón tomaremos como sistema la mínima cantidad de cuerpos de modo que no existan impulsos exteriores en esa dirección y que la masa del sistema permanezca constante.

Vamos a tomar en primer lugar como sistema el bote 2 con toda su carga M y su velocidad v en el instante inicial y como instante final el bote 2 con su carga M-2m y los dos paquetes de masa m con sus velocidades respecto a tierra.

La velocidad de cada paquete respecto a tierra es [latex]\vec{u}+\vec{v}_{2}[/latex] donde la velocidad de arrastre es la velocidad final del bote 2.

[latex]Mv=(M-2m)v_{2}+m(u+v_{2})+m(-u+v_{2})[/latex]

Operando resulta

[latex]Mv=Mv_{2}-2mv_{2}+mu+mv_{2}-mu+v_{2}[/latex]

Simplificando

[latex]Mv=Mv_{2}[/latex]

Luego el segundo bote mantiene su velocidad constante.

[latex]v=v_{2}[/latex]

Para encontrar la velocidad final del bote 1 tomamos como sistema el bote con toda su masa y el paquete que recibe.

Luego

[latex]Mv+m(u+v_{2})=(M+m)v_{1}[/latex]

Como la velocidad del bote 2 es  v operando resulta

[latex]v_{1}(m+M)=(m+M)v+mv[/latex]

Luego

[latex]v_{1}=v+\frac{mu}{m+M}[/latex]

Es decir, la velocidad del primer bote aumenta.

Para hallar la velocidad del tercer bote operando de modo análogo resulta

[latex]Mv+m(-u+v)=(m+M)v_{3}[/latex]

[latex](m+M)v-mu=(m+M)v_{3}[/latex]

y se llega que

[latex]v_{3}=v-\frac{mu}{(m+M)}[/latex]

Es decir que la velocidad del tercer bote disminuye en la misma cantidad que la del primer bote aumenta.

¿Parecen lógicos los resultados alcanzados? ¿Por qué?