3
By the end of this chapter, you should be able to:
- Explain the fundamental concept of the Time Value of Money (TVM) and why it matters.
- Calculate Future Value (FV) and Present Value (PV) using formulas and financial calculators.
- Apply the Rule of 72 for quick financial estimations.
- Understand how compounding frequency affects investment growth.
- Analyze the difference between ordinary annuities and annuity due payments.
- Use financial calculators and apps for solving TVM problems.
- Understand loan amortization and how early payments affect total interest.
3.1 Introduction: Why Time Value of Money Matters
Imagine this:
A wealthy, eccentric billionaire offers you a choice—receive $1 million today or $1.5 million five years from now.
It seems like an easy decision, right? A bigger number should mean a better deal.
But what if inflation over those five years eats away at the purchasing power of that $1.5 million?
What if you could invest the $1 million today and turn it into even more by the time the five years are up?
Suddenly, the “obvious” choice isn’t so obvious anymore.
This dilemma highlights a principle that governs every financial decision you’ll ever make:
Money has a time value.
The Time Value of Money (TVM) is the simple but powerful idea that a dollar today is worth more than a dollar tomorrow—because today’s dollar can be invested, can earn interest, and can grow.
Understanding this principle isn’t just for bankers or stockbrokers; it’s essential for anyone who wants to make smart financial choices.
Whether you are saving for a vacation, paying off a loan, investing for retirement, or simply deciding whether to buy that new phone now or later, TVM is quietly influencing the outcome.
Throughout this chapter, you will learn:
-
- Why Future Value and Present Value matter in everyday life.
- How compounding transforms small savings into significant wealth.
- Why starting early gives you a powerful advantage, even if you start small.
- How to use simple tools like the Rule of 72 to make quick, smart estimates.
- How annuities, loans, and investments all rely on TVM calculations.
Mastering the Time Value of Money doesn’t just make you better at math.
It makes you better at life—because it teaches you how to value your time, your money, and your future.
Let’s dive in.
Terrin, fresh out of college, received two job offers: one with a $5,000 signing bonus today, another offering $7,000 payable after three years. On the surface, $7,000 looked better, but after considering the Time Value of Money and his potential investment returns if he took the $5,000 today, Terrin realized he could grow that money significantly within three years — potentially earning more than the $7,000 promised. He took the $5,000, invested it wisely, and came out ahead.
Lesson: Sometimes “more” later isn’t worth as much as “less” today.
3.2 Understanding the Basics of Time Value of Money
Money is not just a static number sitting in your bank account—it is a living, dynamic resource that changes value over time.
This simple but powerful idea is known as the Time Value of Money (TVM).
At its core, TVM means that a dollar today is more valuable than a dollar tomorrow.
This is because money today can be invested, can earn interest, can appreciate in value, or can be used to seize opportunities that may not exist in the future.
Every financial decision you face—whether it’s buying a house, saving for retirement, paying off a loan, or choosing between two investments—is fundamentally about comparing value across time.
Understanding this concept is the difference between growing wealth and watching it stagnate or decline.
3.2.1 Why Does Money Lose Value Over Time?
There are two major forces at work:
-
- Opportunity Cost:
When you hold onto cash instead of investing or using it productively, you lose the potential growth that money could have achieved. - Inflation:
Inflation reduces the purchasing power of money over time.For example, if inflation averages 3% per year, something that costs $100 today will cost approximately $119 in just six years.
- Opportunity Cost:
Thus, a dollar today can be invested, can work for you, and can help beat the eroding effects of inflation.
3.2.2 TVM in Real Life: Simple Examples
-
- Choosing When to Receive Money:
Imagine you are offered $1,000 now or $1,100 one year from today.
If you could invest the $1,000 at a guaranteed 5% interest rate, you would have $1,050 after one year—not as much as $1,100.
In this case, waiting would be better—unless you could invest at a higher return. - Saving for the Future:
Saving $200 per month starting at age 25 could lead to more wealth by retirement than saving $400 per month starting at age 40.
Time magnifies the impact of consistent action. - Borrowing and Paying Interest:
When you take out a loan, the lender charges you interest because they lose the opportunity to use that money elsewhere.
They are applying the Time Value of Money against you.
- Choosing When to Receive Money:
3.2.3 Key Principle: Money Has Earning Potential
Every dollar has hidden power—the ability to earn more dollars through wise investment, savings, or business opportunities.
The sooner you put your money to work, the greater the rewards.
If you wait too long to invest or save, you are not just losing time—you are sacrificing future growth.
Understanding this is the first step toward making money your ally, rather than your burden.
Paula used to spend about $150 a week on groceries for her family. She noticed that within a year, the same basket of basic groceries—milk, eggs, bread, fruits, and vegetables—was costing her almost $180.
It wasn’t because she was buying fancier items; it was pure inflation. Prices quietly crept up while her budget stayed the same.
This real-world experience made Paula realize that if she left money sitting in a checking account without earning interest, inflation would quietly eat away at its value over time.
3.3 Future Value Concepts
Imagine planting a small tree today.
At first, it looks almost the same week after week.
But with time—and the right environment—it grows taller, stronger, and more valuable.
Money works the same way.
When you invest money today, it can grow over time through earning interest or investment returns.
The measure of what your money will become in the future is called Future Value (FV).
3.3.1 What Is Future Value?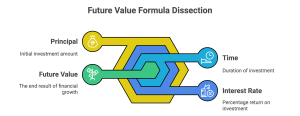
Future Value answers a simple but powerful question:
“If I invest money today, how much will it be worth later?”
It takes into account three critical factors:
-
- The amount you invest (Principal)
- The rate of return (Interest Rate)
- The length of time (Number of Periods)
The basic Future Value formula when interest is compounded annually is:
[latex]FV = PV \times (1 + r)^n[/latex]
Where:
-
- FV = Future Value
- PV = Present Value (initial investment)
- r = Annual interest rate (expressed as a decimal)
- n = Number of years
Example 1: Future Value of a Single Investment
Suppose you invest $1,000 at an annual interest rate of 5% for 10 years.
Solution:
[latex]FV = 1,000 \times (1 + 0.05)^{10}[/latex]\]
[latex]FV = 1,000 \times 1.6289[/latex]
[latex]FV = 1,628.89[/latex]
After 10 years, your $1,000 will grow to approximately $1,628.89.
Notice how the growth accelerates over time, not just because of the original $1,000, but because you are earning interest on the interest each year.
This is called compounding, and it is the most powerful force in personal finance.
3.3.2 Compounding Frequency Matters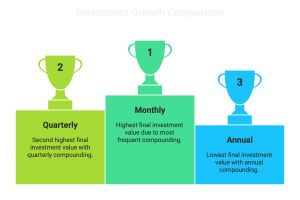
Not all compounding happens just once a year.
In reality, many accounts compound monthly, quarterly, or even daily.
The more frequent the compounding, the faster your money grows.
When interest compounds more often than annually, the formula slightly adjusts:
\[
FV = PV \times \left(1 + \frac{r}{m}\right)^{m \times n}
\]
Where:
-
- m = Number of compounding periods per year
Example 2: Monthly Compounding
You invest $5,000 at 6% annual interest, but interest compounds monthly.
You leave the money invested for 5 years.
Solution:
-
- r = 0.06
- m = 12 (monthly compounding)
- n = 5
\[
FV = 5,000 \times \left(1 + \frac{0.06}{12}\right)^{12 \times 5}
\]
\[
FV = 5,000 \times (1.005)^{60}
\]
\[
FV = 5,000 \times 1.34885
\]
\[
FV = 6,744.25
\]
After 5 years, your $5,000 grows to about $6,744.25.
Notice that monthly compounding adds a little extra growth compared to annual compounding.
3.3.3 Visualizing the Impact of Time
Let’s compare two investors:
-
- Investor A invests $5,000 at 6% for 5 years.
- Investor B invests the same $5,000 at 6% for 30 years.
Using annual compounding:
-
- Investor A’s Future Value ≈ $6,691.13
- Investor B’s Future Value ≈ $28,717.47
Investor B didn’t invest more money; they just invested more time.
The longer the investment horizon, the more dramatic the compounding effect.
3.3.4 Key Lessons About Future Value
-
- Starting early matters more than starting big. Even small amounts invested early can grow significantly.
- Higher interest rates magnify growth, but come with more investment risk.
- More frequent compounding accelerates wealth building.
Waiting costs you money. Delaying saving or investing even a few years can dramatically lower your future wealth.
Alex dreamed of taking a six-month sabbatical to travel the world. He could have easily charged the expenses to his credit cards and worried about it later.
Instead, he made a different choice: he set a savings goal five years in advance.
By contributing $200 a month into a separate high-yield savings account—and letting compound interest work its magic—Alex was able to fully fund his airfare, lodging, and living expenses without taking on a single dollar of debt.
Lesson: Future Value planning turned a dream into reality, without the burden of future payments.
3.4 Present Value Concepts
If Future Value is about imagining how your money will grow,
Present Value (PV) flips the question around:
“What is the value today of a payment or investment I will receive in the future?”
Understanding Present Value helps you make smart choices about saving, investing, borrowing, and spending.
After all, if you are promised $1,000 in five years, you need to know:
How much is that really worth to me today?
3.4.1 What Is Present Value?
Present Value tells us how much a future sum of money is worth today, considering:
-
- The time until you receive it
- The rate of return you could earn elsewhere
- The erosion caused by inflation and opportunity cost
The basic Present Value formula is:
\[
PV = \frac{FV}{(1 + r)^n}
\]
Where:
-
- PV = Present Value
- FV = Future Value
- r = Interest rate (expressed as decimal)
- n = Number of periods (years)
Example 3: Finding the Present Value of a Future Payment
Suppose you are offered $5,000 to be paid 5 years from now.
You believe you could otherwise earn a 6% return annually by investing elsewhere.
Solution:
\[
PV = \frac{5,000}{(1 + 0.06)^5}
\]
\[
PV = \frac{5,000}{1.3382}
\]
\[
PV \approx 3,737.19
\]
Receiving $5,000 in five years is equivalent to having about $3,737.19 today, assuming a 6% return.
Would you rather have $3,800 now or $5,000 later?
Now you have a way to decide rationally.
3.4.2 Why Present Value Matters in Real Life
-
- Saving for Retirement: How much do you need to invest today to have $1 million by retirement?
- Evaluating Investments: Is it better to accept a lump sum today or a series of future payments?
- Loan Comparisons: When comparing loans, banks discount the value of future repayments to see how “expensive” a loan really is.
- Purchasing Decisions: Should you take a rebate now or lower payments spread over time?
In all these cases, Present Value helps you compare apples to apples by adjusting for the time value of money.
3.4.3 Key Factors That Influence Present Value
-
- Interest Rates: Higher rates lower the Present Value (because you could invest and earn more elsewhere).
- Time Horizon: The longer you wait to receive money, the less it is worth today.
Risk: Riskier future payments may require using a higher “discount rate” to compensate for uncertainty.
Example 4: Comparing Two Job Offers
Suppose you are considering two job offers:
-
- Job A: Sign-on bonus of $5,000 today.
- Job B: Sign-on bonus of $6,000 after two years.
Assuming you could earn 5% annual return elsewhere, which offer is better?
Solution:
Find the Present Value of the $6,000:
\[
PV = \frac{6,000}{(1 + 0.05)^2}
\]
\[
PV = \frac{6,000}{1.1025}
\]
\[
PV \approx 5,443.70
\]
Comparing:
-
- Job A bonus today = $5,000
- Job B Present Value = $5,443.70
Even after adjusting for time, Job B offers more real value.
When Carlos was planning to leave his full-time job, he received an offer: either a lump sum bonus if he resigned immediately or a larger bonus if he stayed another two years. Using Present Value analysis, Carlos realized that after adjusting for investment opportunities, the smaller immediate bonus actually worked out better financially — and gave him the flexibility to start his next chapter sooner.
Lesson: Present Value thinking helped Carlos prioritize freedom over delayed (and riskier) rewards.
3.5 The Rule of 72
Imagine you invest money today and wonder:
“How long will it take for my investment to double?”
Sure, you could use complicated math or a financial calculator…
Or you could use one of the simplest and most powerful shortcuts in all of finance:
The Rule of 72.
3.5.1 What Is the Rule of 72?
The Rule of 72 is a mental math trick that estimates how many years it will take for an investment to double, based on its annual interest rate.
The formula is simple:
\[
\text{Years to Double} = \frac{72}{\text{Interest Rate (\%)}}
\]
Where:
-
- 72 is a constant approximation derived from natural logarithms.

- Interest Rate is expressed as a whole number, not a decimal.
- 72 is a constant approximation derived from natural logarithms.
This rule gives you a fast, rough estimate without needing a calculator.
3.5.2 Why 72?
Technically, the mathematical constant that would make this formula exact is closer to 69.3.
However, 72 is used because:
-
- It is easier to divide mentally (since it is divisible by 2, 3, 4, 6, 8, 9, and 12).
- It gives surprisingly close approximations for typical investment rates between 4% and 12%.
Thus, it strikes the perfect balance between accuracy and simplicity.
Example 5: Using the Rule of 72
Suppose you invest your savings in a fund earning an average of 6% per year.
Question: How long will it take for your money to double?
Solution:
\[
\text{Years to Double} = \frac{72}{6} = 12\ \text{years}
\]
At a 6% return, your money would roughly double every 12 years.
Example 6: Finding the Needed Rate to Double Faster
Suppose you want to double your investment in 9 years.
Question: What approximate interest rate would you need?
Solution:
\[
\text{Required Rate} = \frac{72}{9} = 8\%
\]
You would need an 8% annual return to double your money in 9 years.
Alex knew that paying for college would be one of the largest financial commitments he would face as a parent. The rising cost of tuition seemed overwhelming, and planning 15 to 18 years ahead felt almost impossible to wrap his mind around.
Instead of feeling paralyzed, Alex decided to start small and early. He used the Rule of 72 as a simple tool to project how his savings could grow over time. By realizing that his investments could double every 9 to 10 years with a modest return, the goal became much more tangible.
He set up automatic monthly contributions into a dedicated education account. Even modest amounts, started early enough, would have time to double—and possibly double again—before his kids reached college age.
Lesson: When the future feels distant and overwhelming, simple tools like the Rule of 72 can turn long-term goals into manageable action plans.
3.6 Compound Interest and Compounding Frequency
If simple interest is like planting a tree and letting it grow on its own,
compound interest is like planting a tree that grows more trees, which in turn grow even more trees.
It’s the phenomenon that Albert Einstein allegedly called:
“The most powerful force in the universe.”
Understanding how compounding works—and how often it happens—can transform your financial future.
3.6.1 What Is Compound Interest?
Compound interest means that you earn interest not only on your initial principal but also on the accumulated interest from previous periods.
In other words: Interest on interest.
Over time, this snowball effect accelerates growth dramatically compared to simple interest (where you only earn interest on the original amount).
3.6.2 The Basic Formula for Compound Interest
\[
FV = PV \times \left(1 + \frac{r}{m}\right)^{m \times n}
\]
Where:
-
- FV = Future Value
- PV = Present Value (initial investment)
- r = Annual interest rate (as a decimal)
- m = Number of compounding periods per year
- n = Number of years
Example 7: Annual Compounding
You invest $1,000 at 5% annual interest, compounded once a year for 10 years.
Solution:
\[
FV = 1,000 \times (1 + 0.05)^{10}
\]
\[
FV = 1,000 \times 1.6289
\]
\[
FV = 1,628.89
\]
After 10 years, your investment grows to $1,628.89.
3.6.3 Compounding Frequency: Why It Matters
The more frequently interest is compounded, the more often your money earns new interest.
This leads to slightly higher returns over time.
Example 8: Comparing Compounding Frequencies
Suppose you invest $5,000 at an annual interest rate of 6% for 5 years.
- Annual Compounding:
- \[
FV = 5,000 \times (1 + 0.06)^5 = 5,000 \times 1.3382 = 6,691.13
\]
- \[
- Monthly Compounding:
- \[
FV = 5,000 \times \left(1 + \frac{0.06}{12}\right)^{12 \times 5}
\] - \[
FV = 5,000 \times (1.005)^{60}
\] - \[
FV = 5,000 \times 1.34885
\] - \[
FV = 6,744.25
\]
- \[
With monthly compounding, you end up with about $53 more after five years.
It might seem small over short periods, but over decades or with large investments, it makes a massive difference.
3.6.4 Continuous Compounding (Advanced Concept)
In theory, if you could compound infinitely often—every fraction of a second—you would achieve continuous compounding.
The formula changes slightly:
-
- \[
FV = PV \times e^{r \times n}
\]
- \[
Where e is Euler’s number (~2.71828), a constant in mathematics.
While continuous compounding is mostly theoretical, it’s used in some advanced financial modeling.
3.6.5 Key Insights on Compounding
-
- Frequency Matters: More frequent compounding = more growth.
- Time Matters Even More: The longer you leave your money to compound, the more powerful the snowball becomes.
- Small Differences Add Up: Choosing a monthly compounding account over an annual one can mean thousands of dollars over 20–30 years.
Early Action Wins: Even modest early investments can outperform large late investments because of compounding.
When they graduated college, Mia and Jake both promised themselves they’d start investing “someday.”
Mia took action right away. She invested $200 a month starting at age 22 — but after just 10 years, life got busy, and she stopped contributing completely at 32.
Jake, on the other hand, didn’t start investing until he turned 32. He then diligently contributed $200 a month all the way until he retired at 65.
At first glance, you’d expect Jake to come out ahead — after all, he invested for 33 years while Mia only invested for 10. But here’s the surprise:
- By retirement, Mia’s early start and compounding magic grew her account to approximately $380,000.
- Jake, even after investing three times longer, ended up with around $270,000.
Lesson: Mia invested far less money — but because her dollars had more time to grow, she ended up wealthier. When it comes to building wealth, starting early beats investing more later.
3.7 Annuities and Their Applications
Not all financial decisions involve lump sums paid all at once.
Sometimes, money flows in regular, equal payments over time.
Saving for retirement, paying off a mortgage, or receiving a pension—these are all examples of annuities in action.
Understanding how annuities work will help you manage both saving and borrowing more wisely.
3.7.1 What Is an Annuity?
An annuity is a series of equal payments made at regular intervals over a specified period.
Annuities can involve:
-
- Paying money out (e.g., making fixed monthly loan payments).
- Receiving money in (e.g., collecting pension checks during retirement).
Each payment includes principal and interest, and the timing of payments affects the overall value.
Ordinary Annuity: Payments made at the end of each period (e.g., most loans, mortgages).
Annuity Due: Payments made at the beginning of each period (e.g., rent payments).
Timing matters:
Annuity Due will accumulate slightly more future value because payments are invested earlier.
3.7.2 Future Value of an Annuity
If you consistently save and invest a fixed amount every period, you can calculate how much money you will accumulate in the future.
The Future Value of an Ordinary Annuity formula is:
\[
FV = P \times \left( \frac{(1 + r)^n – 1}{r} \right)
\]
Where:
-
- P = Payment amount per period
- r = Interest rate per period
- n = Total number of periods
Example 9: Building Retirement Savings
You decide to invest $500 monthly into an account earning 6% annual interest, compounded monthly, for 30 years.
Solution:
\[
r = \frac{0.06}{12} = 0.005
\]
\[
n = 30 \times 12 = 360
\]
\[
FV = 500 \times \left( \frac{(1 + 0.005)^{360} – 1}{0.005} \right)
\]
\[
FV \approx 500 \times 995.51
\]
\[
FV \approx 497,755
\]
After 30 years, you would accumulate approximately $497,755.
Notice: Most of the money comes not from your contributions but from the magic of compound interest!
3.7.3 Present Value of an Annuity
What if you are promised a series of future payments and want to know how much they are worth today?
The Present Value of an Ordinary Annuity formula is:
\[
PV = P \times \left( \frac{1 – (1 + r)^{-n}}{r} \right)
\]
This is crucial for:
-
- Valuing pensions and insurance payouts.
- Calculating loan balances.
- Pricing lottery winnings or structured settlements.
Example 10: Valuing a Pension
You expect to receive $20,000 per year for 15 years in retirement.
Assume a discount rate of 5% annually.
Solution:
-
- P = 20,000
- r = 0.05
- n = 15
\[
PV = 20,000 \times \left( \frac{1 – (1 + 0.05)^{-15}}{0.05} \right)
\]
\[
PV \approx 20,000 \times 10.3797
\]
\[
PV \approx 207,594
\]
The present value of your pension payments would be approximately $207,594 today.
3.7.4 Special Case: Perpetuities
A perpetuity is an annuity that lasts forever—an endless series of payments.
The formula simplifies to:
\[
PV = \frac{P}{r}
\]
While true perpetuities are rare, the concept is useful for valuing certain investments like preferred stock.
3.7.5 Real-World Applications
-
- Saving for Retirement: Systematic contributions build wealth through future value of annuities.
- Loans and Mortgages: Fixed monthly payments are present value calculations based on annuity formulas.
- Pensions and Insurance: Companies use annuity math to price how much future payment streams are worth today.
Daniel was offered two options when buying his first home:
- A 15-year mortgage with high monthly payments but less total interest.
- A 30-year mortgage with lower payments, freeing up extra cash every month.
Most people might rush toward the 15-year option to “save interest.” But Daniel thought differently.
He chose the 30-year mortgage and used the extra money he saved each month to invest in a low-cost index fund averaging 7% annual returns.
Over 30 years:
- Yes, he paid around $90,000 more in mortgage interest.
- But his investment portfolio grew to over $300,000 — more than tripling what he “lost” in extra interest.
Lesson: The goal isn’t just to minimize interest — it’s to maximize total wealth. Managing opportunity cost wisely often beats focusing only on debt payoff.
3.8 Using Financial Calculators and Apps
By now, you’ve seen that Time Value of Money (TVM) calculations can get a little heavy:
Exponents, discounting, compounding, multiple time periods…
Luckily, in the real world, you don’t need to calculate everything by hand.
Financial calculators and mobile apps can make solving TVM problems fast, accurate, and easy—if you know what inputs they require.
3.8.1 Why Use a Financial Calculator?
-
- Saves time: Complex problems are solved in seconds.
- Reduces errors: No more misplacing parentheses or miscalculating exponents.
- Realistic: In business, finance, and personal decision-making, professionals use these tools daily.
Even if you understand the formulas conceptually (which you should),
using technology properly is part of real financial literacy.
3.8.2 Common TVM Functions on a Calculator
Most financial calculators (like the Texas Instruments BA II Plus or smartphone apps) work with a set of standard TVM keys:
- N
- Number of periods.
- I/Y
- Interest rate per year.
- PV
- Present Value
- PMT
- Payment amount per period
- FV
- Future Value
- CPT
- Compute (calculate the unknown)
Tip: You must enter four variables, then solve for the fifth.
Example 11: Solving for Future Value (Single Lump Sum)
You invest $5,000 today at 7% interest for 8 years.
What will it be worth?
Inputs:
-
- PV = –5,000 (entered as negative because it’s an outflow)
- I/Y = 7
- N = 8
- PMT = 0 (no payments during the period)
Steps:
-
- Press CPT → FV
The calculator will show approximately $8,590.40.
Example 12: Solving for Present Value of a Future Payment
You want $15,000 in 5 years for a down payment.
If you can earn 5% interest, how much should you invest today?
Inputs:
-
- FV = 15,000
- I/Y = 5
- N = 5
- PMT = 0
Steps:
-
- Press CPT → PV
The calculator will display approximately $11,739.09.
Example 13: Solving for Payment on a Loan (Annuity)
You borrow $20,000 for a car loan at 6% interest for 5 years, compounded monthly.
Inputs:
-
- PV = 20,000
- I/Y = 6 ÷ 12 = 0.5 (monthly rate)
- N = 5 × 12 = 60 (total number of months)
- FV = 0 (you want to fully pay off)
Steps:
-
- Press CPT → PMT
You find your monthly payment is approximately $386.66.
3.8.3 Popular Apps for TVM Calculations
If you don’t have a dedicated financial calculator, these apps are great alternatives:
-
- Financial Calculator BA Plus (iOS/Android)
- HP 12C Financial Calculator (classic finance industry standard)
- Easy Money Planner (iOS/Android) for budgeting and TVM
Many banking and investing apps also have built-in calculators for mortgages, investments, and retirement projections.
3.8.4 Practical Tips for Using Calculators and Apps
-
- Always check your settings: Make sure you are calculating with the correct number of periods and the right interest rate format (annual vs. monthly).
- Watch signs:
- Money you pay out (invest, deposit) = negative.
- Money you receive = positive.
- Understand what you’re solving for: Don’t just punch numbers—know what the answer represents.
- Practice solving by hand first: Build intuition before trusting a calculator.
Technology is a tool, not a replacement for financial thinking.
3.9 Amortized Loans: Paying Off Debt
Borrowing money isn’t free.
When you take out a loan—whether for a car, a home, or an education—you agree not just to repay the original amount, but also to pay interest over time.
Most loans you encounter are amortized loans, which means:
-
- You make equal payments over time.
- Each payment includes both interest and principal repayment.
- Over time, the interest portion shrinks, and the principal portion grows.
Understanding amortization can save you thousands of dollars in your financial life.
3.9.1 What Is Loan Amortization?
Loan amortization refers to the gradual reduction of your loan balance through scheduled, regular payments.
Each payment does two things:
-
- Pays off interest owed for the period.
- Reduces the outstanding principal balance.
Early in the loan, most of your payment goes toward interest.
Later in the loan, most of your payment goes toward reducing principal.
3.9.2 The Basic Loan Payment Formula
The standard monthly loan payment (for fixed-rate loans) can be calculated with:
\[
PMT = P \times \frac{r(1 + r)^n}{(1 + r)^n – 1}
\]
Where:
-
- PMT = Monthly payment
- P = Principal (amount borrowed)
- r = Monthly interest rate (annual rate ÷ 12)
- n = Total number of monthly payments
Example 14: Calculating a Car Loan Payment
You borrow $20,000 for a new car.
The loan has a 5% annual interest rate and a term of 5 years.
Solution:
-
- Principal (P) = 20,000
- Annual Rate = 5% → Monthly Rate = 0.05 ÷ 12 = 0.004167
- n = 5 × 12 = 60 months
Apply the formula:
\[
PMT = 20,000 \times \frac{0.004167(1 + 0.004167)^{60}}{(1 + 0.004167)^{60} – 1}
\]
Your monthly car payment would be approximately $377.42.
3.9.3 Understanding the Payment Breakdown
In the first month, most of the $377.42 payment goes toward interest.
As months go by:
-
- The interest portion decreases.
- The principal repayment portion increases.
The total payment remains the same.
Example 15: First Month Breakdown
From Example 1:
-
- Loan balance: $20,000
- Monthly interest rate: 0.4167%
First month’s interest:
\[
\text{Interest} = 20,000 \times 0.004167 = 83.34
\]
First month’s principal repayment:
\[
\text{Principal} = 377.42 – 83.34 = 294.08
\]
After the first payment:
-
- You pay $83.34 in interest.
- You reduce the principal by $294.08.
\[
\text{New Balance} = 20,000 – 294.08 \approx 19,705.92
\]
3.9.4 How Loan Terms Affect Your Total Cost
-
- Longer loan terms mean lower monthly payments but much more total interest paid.
- Shorter loan terms have higher payments but save money in interest overall.
Example:
-
- 30-year mortgage = smaller payments, more interest paid.
- 15-year mortgage = bigger payments, less interest overall.
Always consider not just the monthly payment, but the total cost of borrowing.
3.9.5 Prepaying a Loan: Smart Strategy?
Paying a little extra toward the principal each month can:
-
- Reduce the loan term significantly.
- Save thousands in interest.
However, check for prepayment penalties on your loan agreement before making extra payments.
3.9.6 Real-World Applications
-
- Mortgages: Fixed monthly payments over 15 to 30 years.
- Car Loans: Common terms of 3 to 7 years.
- Student Loans: Typically 10 to 20 years, with amortized payments.
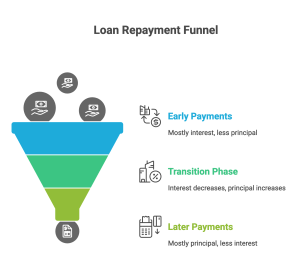
Each of these loans uses the same core amortization logic.
3.9.7 Key Takeaways on Amortized Loans
-
- Fixed payments simplify budgeting, but understand the interest-principal shift over time.
- Total interest paid depends heavily on term length and rate.
- Early payments mostly cover interest, later payments mostly reduce principal.
- Prepaying principal early can be one of the smartest financial moves you make.
Knowing how your loan works is just as important as getting a good interest rate.
- A dollar today is worth more than a dollar tomorrow due to its earning potential.
- Future Value shows what today’s investments will become over time; Present Value shows what future money is worth today.
- Compound interest and frequent compounding accelerate wealth growth.
- The Rule of 72 is a practical tool for estimating doubling time.
- Annuities help structure regular savings and payments.
- Financial calculators and apps make solving TVM problems easier but require conceptual understanding.
- Loan amortization schedules split payments into interest and principal portions, changing over time.
- Prepaying loans early can save significant interest over the life of a loan.
When Kevin bought his second home, he set up automatic extra payments of $100/month toward principal. This tiny addition shaved off almost 4 years from his 30-year mortgage and saved him over $40,000 in interest payments.
Lesson: Small consistent efforts early in a loan’s life can create massive long-term savings.
Conceptual Questions
- Explain the Time Value of Money (TVM) in your own words.
Why is a dollar today more valuable than a dollar received in the future? - Describe the three key factors that affect the Future Value of an investment.
How does each one influence the outcome? - What is the difference between simple interest and compound interest?
Provide a real-life example where compounding makes a significant difference. - How does compounding frequency impact the growth of an investment?
Compare the effects of annual, monthly, and daily compounding on a $1,000 investment at 5% interest for 5 years. - In the context of Present Value, what does a higher discount rate indicate?
Explain how risk and opportunity cost are reflected in the discount rate used. - Summarize the Rule of 72.
What does it allow you to estimate quickly, and under what conditions might it be less accurate? - Compare an Ordinary Annuity and an Annuity Due.
Give a financial example for each and explain which one has a higher future value, all else being equal. - What is loan amortization, and why is it important for borrowers to understand how their payments are structured?
Explain what happens to the interest and principal portions of a loan over time. - Why is early saving or investing considered a critical strategy for maximizing financial growth?
Support your answer with a discussion of compounding and time. - How do financial calculators and apps enhance decision-making when working with Time Value of Money problems?
Why should a financial professional still understand the underlying concepts even when using technology?
Problem Solving Questions
- Future Value with Annual Compounding
You invest $3,000 today into an account earning 7% annual interest, compounded annually.
How much will you have in 10 years?
- Future Value with Monthly Compounding
You deposit $8,000 into a savings account paying 6% annual interest, compounded monthly.
What will the account balance be after 5 years?
- Present Value of a Future Payment
You want to have $20,000 saved for a down payment in 6 years.
Assuming an annual return of 5%,
how much should you invest today to reach your goal?
- Rule of 72 Application
If you invest in a fund that earns 9% annually,
approximately how long will it take for your money to double using the Rule of 72?
- Comparing Two Investments
Investment A offers 5% annual interest, compounded annually.
Investment B offers 4.8% annual interest, compounded monthly.
Which investment yields a higher effective annual rate (EAR)?
- Annuity: Future Value of Retirement Savings
You plan to save $400 per month into a retirement account earning 6% annual interest, compounded monthly, for 25 years.
How much will you have at the end of the 25 years?
- Annuity: Present Value of Lottery Winnings
You win a lottery that pays you $50,000 per year for 20 years.
Assuming a discount rate of 5%,
what is the present value of your winnings today?
- Loan Payment Calculation
You take out a loan for $15,000 to buy a car.
The loan has an interest rate of 6%, and you agree to repay it over 5 years with monthly payments.
What is your required monthly payment?
- Early Prepayment Impact
Suppose you make an extra payment of $2,000 toward your mortgage principal early in the loan term.
How will this affect the total interest paid and the loan term?
(Explain conceptually, no calculation required.)
- Future Value vs. Present Value Reasoning
You are offered two options:
- Option A: Receive $10,000 today.
- Option B: Receive $12,000 five years from now.
Assuming you can earn 5% annually by investing elsewhere,
which option is financially better, and why?
Interactive Challenges
- Quick Decision: When Does Money Double?
You hear about three different investments:
- Investment A: 6% annual return
- Investment B: 8% annual return
- Investment C: 12% annual return
Using the Rule of 72, match each investment with the approximate number of years needed to double the money.
Options:
- 6% → ______ years
- 8% → ______ years
- 12% → ______ years
- Choose the Best Compounding Option
You have $10,000 to invest.
Which compounding method would result in the highest future value after 10 years?
- A) 6% compounded annually
- B) 6% compounded quarterly
- C) 6% compounded monthly
- D) 6% compounded daily
Select the best option and explain why.
- Identify the Mistake: Interest vs. Principal
A borrower claims:
“Every payment I make on my loan goes entirely toward reducing the loan balance.”
Question:
What mistake are they making?
Explain how amortized loans actually allocate payments over time.
- Real-World Comparison: Lump Sum vs. Stream of Payments
You are offered two job bonuses:
- Bonus A: $10,000 today.
- Bonus B: $2,200 per year for the next 5 years.
Assuming a 5% interest rate,
which bonus has a higher present value?
(Provide a short explanation, no detailed calculation required.)
- Savings Plan Adjustment
You plan to save $300 per month for 20 years at a 7% annual return.
After the first five years, you unexpectedly receive a raise.
Question:
If you increase your monthly savings to $400 starting in year 6,
how will this impact your final retirement balance compared to sticking with $300 monthly?
(Answer conceptually.)
- Strategy Challenge: Paying Off Debt Faster
You have a 30-year mortgage but receive a salary bonus every year.
Which strategy will save you more in total interest paid?
- A) Applying the full bonus toward the mortgage principal each year.
- B) Keeping the bonus in a savings account earning 1% interest.
Explain your reasoning based on the Time Value of Money principles.
- Timeline Building: Compounding Growth
Sketch a timeline showing what happens to a $1,000 investment growing at 8% interest for 5 years, with:
- Annual compounding.
- Monthly compounding.
Label how the compounding frequency affects the growth curve.
- Future Value Estimation: Estimating in Your Head
Without using a calculator, estimate:
If you invest $2,500 at 9% interest,
about how many years will it take to reach $5,000?
(Use mental math based on Rule of 72.)
