43 Basic Equations

 

Introduction:

This module will cover basic equations, order of operations, integers, and evaluating algebraic expressions. You will go have content explained through examples then have an opportunity to practice those skills with exercises.

Topic 1: Order of Operations

 

There is a standard way to do a series of operations (add, subtract, multiply and divide.) This is called the order of operations. The infamous way of remembering the order of operations is B.E.D.M.A.S. This stands for Brackets, Exponents, Division/Multiplication, Addition/Subtraction. This means, in an expression, evaluate what is in the brackets first, then the exponents. Division and multiplication are done from left to right. Finally, addition and subtraction are done from left to right. If necessary, review this section in the math essentials course.

Practice Exercises

[h5p id=”26″]

Topic 2: Integers

Numbers are broken down into groups. Each group is a little more complicated than the previous, and, in a way, the development of the groups reflects the development of mankind’s understanding and need for more complicated math.

• Whole numbers are the most primitive. They are the numbers you can count on your hand: 1, 2, 3, 4, 5 and so on.
• Natural numbers include all whole numbers, plus the number zero.
• Integers include all natural numbers, and all negative numbers. For example, integers are
• …-3,-2.-1.0,1,2,3…

  You can imagine the development of integers was necessary once people started trading goods and money. A negative number meant that you owed someone or paid something.

Adding Integers

When learning about integers, it might be useful to think of numbers as two different qualities: black or red, left or right, or, negative or positive.

Another way of thinking about integers is to “forget” about subtraction or addition. There is one operation that combines integers, and it is like addition. There is no subtraction, only adding negative numbers.

When adding integers, it is useful also to think about movement on a number line.

Example:

Calculate 3 – 4

Note:

• When there is no sign in front of a number, that means it is positive: (+3) – 4
• There is no subtraction. The negative describes the “quality” of the 4: (+3) + (-4)
• The sign in the middle looks like an addition, but it is really the operation that combines integers.

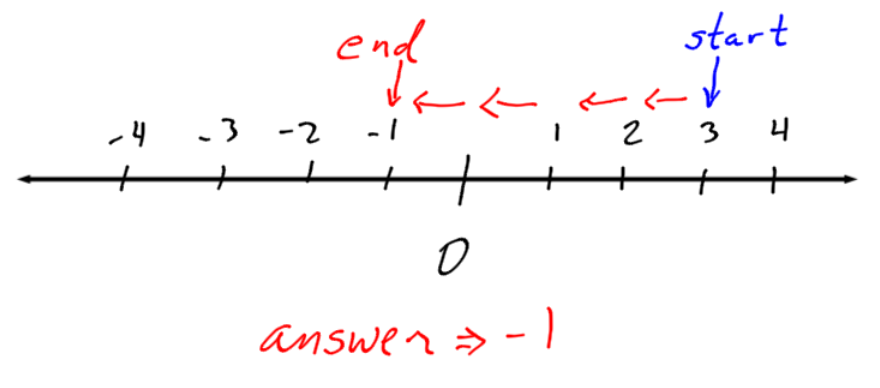
The steps to add integers:

• Start at the number on the left (+3)
• Move the number of spaces indicated by the second number (4)
• Move to the left if the number is negative, or to the right if the number is positive.

Example:

Calculate -5 + 2. This can be rewritten as (-5) + (+2)

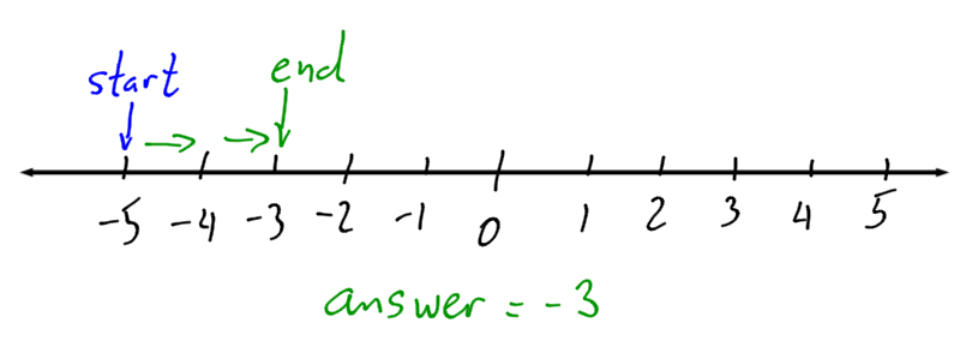
The steps to add integers:

• Start at the number on the left (-5)
• Move the number of spaces indicated by the second number (2)
• Move to the left if the number is negative, or to the right if the number is positive.

Example:

Calculate (-3) – (-2)

In some cases, the question is written as a subtraction question. Think of each negative sign as a change in direction along the number line.

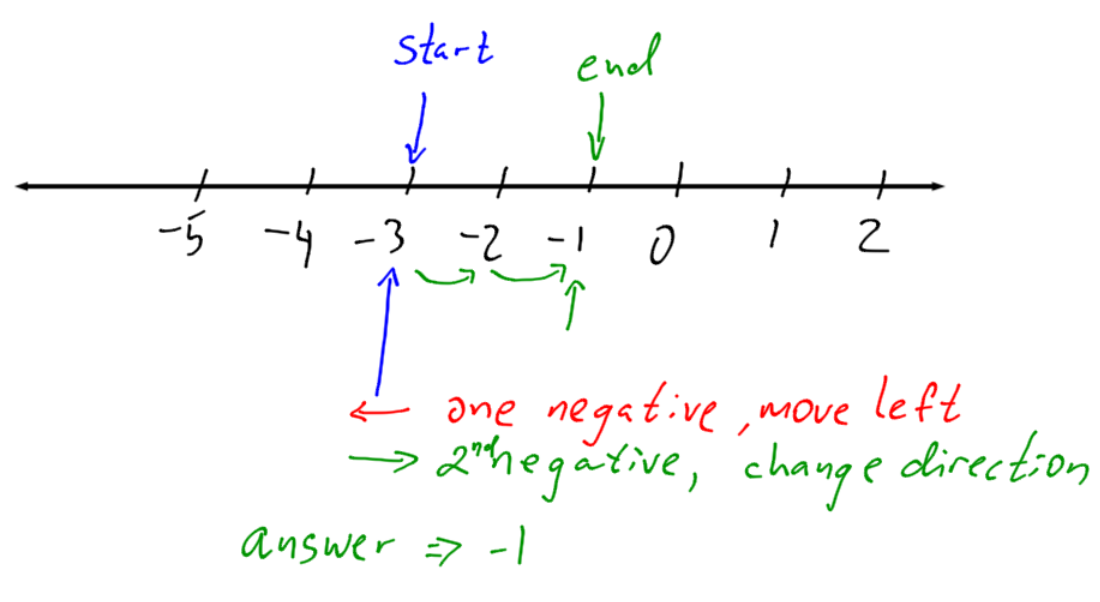
When there are two negatives in a row, they can be replaced by a single positive.

We can draw a conclusion:

If the largest number is negative, the answer will be negative. If the largest number is positive, the answer will be positive.

Practice Exercises: Adding Integers

[h5p id=”27″]

Multiplying Integers

When multiplying integers, the numbers are multiplied as normal, but, will the answer be positive or negative?

This chart helps us determine if the answer will be positive or negative:

One way to help remember this is that the only time the answer is positive is when both factors (numbers multiplied together) are the same sign.

It seems strange that a negative multiplied by a negative is a positive. It might make sense if you consider the famous expression “My enemies’ enemy is my friend.” Another way to look at it is when we were adding two negatives. Each negative changed the direction of movement on the number line. The result was moving to the right.

It can be confusing trying to figure out of a question is a multiplication or an addition/subtraction. Generally, if there is no positive or negative sign separating the numbers, the question is a multiplication sign by default.

Example:

The question -3 + (-2) is an addition question, but the question (-3)(-2) is a multiplication. There is a sign in front of the negative 2, but there is no sign between the brackets.

One final note: the above table applies only when multiplying numbers. Don’t be tempted to use it in an addition or subtraction problem.

Example:

Multiply the following numbers:

• -2(+3)

There is no sign between the bracket and the 2, so the question is a multiplication. The first number is negative, the second positive, so the answer will be negative. The answer is -6.

• (-2)(-3)

Another way of writing multiplication is having both numbers in brackets. Both numbers are negative so the answer is positive. The answer is 6.

• 2×-3

Another, more common way, of writing multiplication is with the “×” sign. The first number is positive, the second negative, so the answer will be negative. The answer is -6.

• 2∙3

Another way to write multiplication is with a dot between two numbers. This is more common in upper level math, and you will not likely come across this in this course. Both numbers are positive, so the answer is positive. The answer is positive 6.

Practice Exercises: Multiplying Integers

[h5p id=”29″]

Dividing Integers and Fractions

Division is really multiplication by the reciprocal. The reciprocal is the “flip” of the number.

Example:

The reciprocal of is . The reciprocal of is , or simply 5.

Example:

Calculate the following:

This basic example can be turned into a multiplication:

For such a basic example, it looks ridiculous to multiply by the reciprocal. However, multiplying by the reciprocal makes more sense in the following example:

Change this into a multiplication problem by multiplying by the reciprocal of the number on the right:

All the sign rules for multiplication apply for division.

Practice Exercises: Dividing Integers

[h5p id=”30″]

2. Divide the following fractions by multiplying by the reciprocal.

1. 
2. 
3. 
4. 

Answer Key

Topic 3: Evaluating Algebraic Expressions

You can use variable in algebra to represent numbers. These variables can be used to express number relationships, such as in the formula A=LxW (area equals length times width.)

A variable is a letter that is used to represent one or more numbers. The numbers are the values of the variable. An algebraic expression is a collection of numbers, variables, operations, and grouping symbols. Here are some examples. Note, that with variables, the multiplication sign is not written down.

Algebraic Expression	Meaning
	8 times y
	x times y
	3 times z plus 2
	5 times a plus 3- all divided by b

When each variable in an algebraic expression is replaced by a number, we are evaluating the expression. For example, if an expression is 8y, and y = 2 we substitute the y with a 2. Therefore, 8y is 8 × 2 or 16.

To evaluate an expression, you can follow these steps:

• Write the expression
• Substitute the numbers given for variables in the expression
• Follow the order of operations to come to the answer

Example 1

The area of a triangle is written using an algebraic expression like:

The base of the triangle is 3 cm, and the height is 5 cm. Substitute the variables for the numbers.

Calculate the value following the order of operations:

3 × 5 ÷ 2 =

The answer is 7.5.

 

Example 2

Use a calculator to calculate the expression when and .

Substitute the variables for the numbers

Follow these keystrokes on your calculator:

The answer is 13.255 rounded to the thousandth.

Practice Exercises

[h5p id=”31″]

Topic 4: Solving Equations with Addition and Subtraction

Instructions

• Go through the content and examples with the group, leaving opportunities for questions.
• Have students complete the practice exercises independently, then take up the answers.

In this topic, we will talk about equations and solutions. These are different than expressions discussed in the last topic. An easy way to tell the difference is: an equation has an equal sign; an expression does not. You simplify an expression by substituting in values. You solve an equation to find out what a variable is.

An equation consists of two expressions: one on either side of an equal sign. It is good to think of this as a balance, with the equal sign being the fulcrum of the balance.

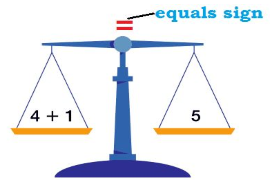
To solve and equation means to isolate the variable. The variable must be on one side of the equal sign alone.

The goal of solving an equation is to keep the scale balanced. If you take away something from one side, you must take it away from the other. If you add something to one side, you must add it to the other.

Example 1:

Solve for the variable x.

As was stated before, the equation has two expressions: one on either side of the equal sign (5+x on the left hand side, and 10 on the right hand side.)

Before we start, we can imagine that x will be 5. (What number, when added to 5, equals 10?)

To solve the equation algebraically, we must get x on one side of the equation, alone.

Mathematical Step	What I’m Thinking
	What is preventing x from being alone? The 5.
	Take 5 away from the left side, and the right side, to keep things in balance.
	Rewrite the equation, simplifying the expressions on either side.

Example 2:

Solve for y:

y-2=7

Before we start, we can imagine that y will be 9. (What number, after subtracting 2, will equal 7?)

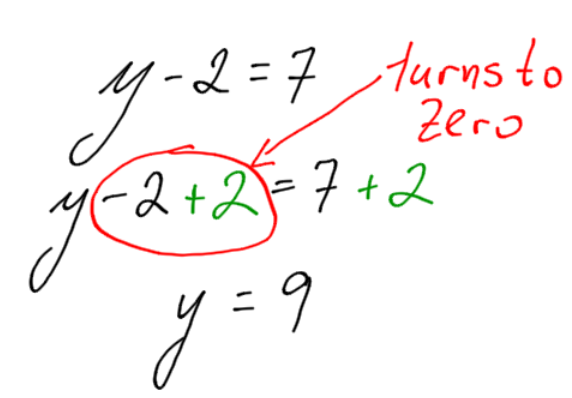
Example 3:

Solve for a:

In this example, there is a negative sign in front of a. Remember, when solving, a needs to be completely alone- not even with a negative sign.

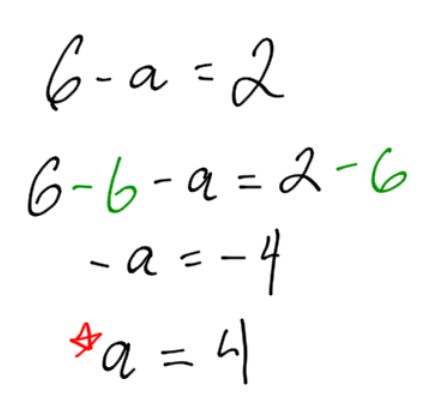
Notice the last line. We went from

directly to

There are a couple of ways of thinking about this. You can multiply both sides by -1 (negative one). Or, you add

Practice Exercises: Solving equations with addition and subtraction

[h5p id=”32″]

Topic 5: Solving Equations with Multiplication and Division

If a number is multiplied to the variable, to “get rid of” that number, you must multiply by the reciprocal.

 

Example:

Solve the equation:

In this example, the variable x needs to be isolated.

Mathematical Step	What I’m Thinking
	What is preventing x from being alone? The 13. The 13 is multiplied to x because there is no sign (add or subtract) between them.
	Multiply both sides by the reciprocal. The reciprocal of 1/3 is 3/1 (or just 3). The order we multiply is not important. (for example, 5 x 3 is the same as 3 x 5).
	Rewrite the equation, simplifying the expressions on either side.

Example:

Solve the equation:

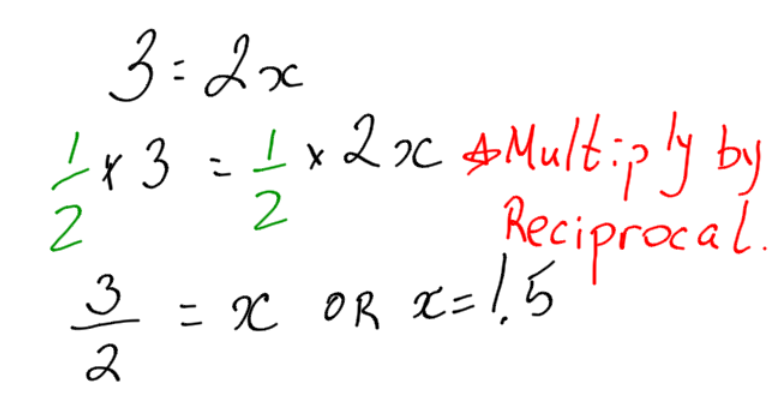
The fact that the variable is on the right hand side of the equation does not matter. 1.5 = x is the same as x = 1.5.

Multiply by the reciprocal may be new and confusing to you. You may have written this out like this in the past:

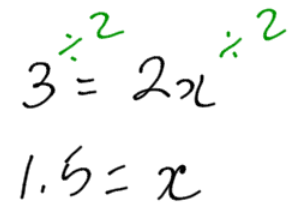
This means you are dividing both sides by 2 which is the same as multiplying by the reciprocal (1/2). Where multiplying by the reciprocal becomes a lot easier and faster is when you have fractions in front of the variable.

Example:

Solve the equation:

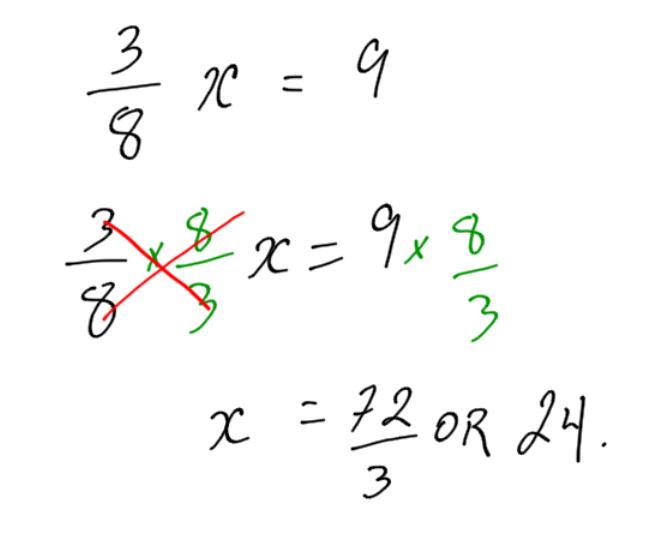
If an equation is written with a division sign (not usual), then use multiplication

Example:

Solve for x:

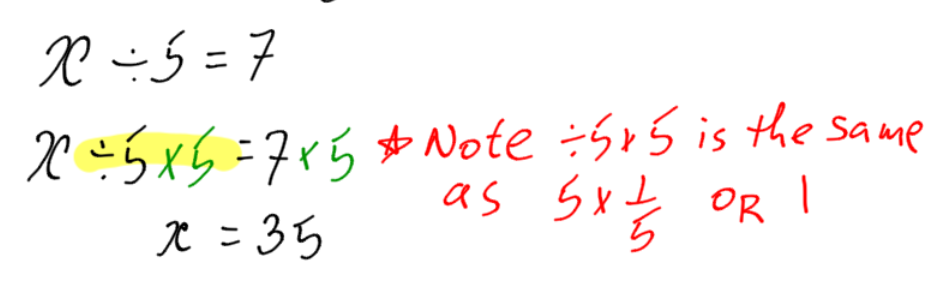
In some cases, the variable will be in the denominator. First multiply by the variable.

Example:

Solve for y:

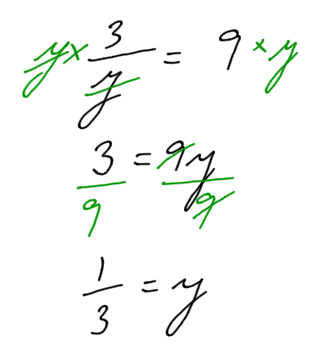
If there is a negative number in front of the variable, multiply by the negative reciprocal.

Example:

Solve for y:

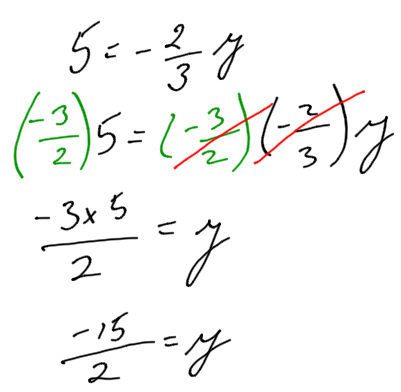
Practice Exercises: Solving Equations with Multiplication and Division

[h5p id=”33″]

Solve the following equations by multiplying by the reciprocal:

1.

 

2.

 

3.

 

4.

 

5.

 

Answers:

1. , 2. , 3., 4. , 5.

Topic 6: Solving Equations involving Roots and Exponents

We will learn how to solve equations involving roots and exponents. This is important because many equations have a squared term in them, for example, the area of a circle is:

or Pythagoras’ theorem:

To solve for the variable, we need to get the variable completely alone- not even with an exponent.

Exponents

Exponents are repeated multiplication. For example,

That is, two to the power of four is two multiplied by itself four times.

With the expression , the number two is called the base and the number four is called the exponent.

Variables can be exponentiated as well as numbers. For example,

Calculating Exponents with your Calculator

Example:

a) Calculate

In your calculator, type 3 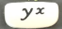5 . The answer will be 243. This is the same as 3 x 3 x 3 x 3 x 3. Note, in this case you need to use the equals button.

b) Calculate (or five cubed.)

There is a special shortcut button for cubed in your calculator. See the above diagram. In your calculator, type 5 . The answer is 125.

c) Calculate

Because squaring is such a common operation, there is a button specifically for it. In your calculator, press 18 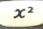. The answer returns immediately as 324.

Roots

A root is the “opposite” operation of an exponent. This is called the “inverse operation” in math language, but what we need to know is that it “undoes” an exponent. Taking the root of an expression is how we will be able to isolate the variable from the exponent.

For example, the square root of 9 is the number that, when multiplied by itself twice, equals 9. This, when written mathematically looks like this:

In mathematical terminology, the number 9 is called the radicand, the number 2 is called the index and the sign is called the radical sign.

The opposite statement is:

We can draw the conclusion that:

What this means in simple terms is that if we want to get rid of the exponent (2) we take the square root and end up with only the base (3). This is what we are going to use to isolate the variable from the exponent in an equation.

The index of a radical can be any number, just like an exponent can be any number:

• When the index of the radical is two, the radical is called “the square root.” If a number has an exponent of two, that number is called “squared.” Note also that the radical sign without any index () means square root ().
• When the index of the radical is three, the radical is called “the cube root.” If a number has an exponent of three, that number is called “cubed.” The three is always written as part of the radical sign ().
• There can be any number for the index. For example, the index of 4 would be called “the fourth root.”

Calculating Roots with your Calculator

Example:

a) Calculate . Round your answer to the nearest tenth.

In your calculator, type 23 . The answer will return without pressing the equals button. The answer is approximately 4.8.

b) Calculate .  In your calculator, type 15 . The answer will return without pressing equals. The answer is approximately 2.5.

c) Calculate .  In your calculator, type 6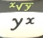4 4 . The answer is approximately 2.8. Note in this case you need to use the equals button.

Practice Exercises: Exponents and Roots

[h5p id=”34″]

 

Calculate the following using your calculator:

1.

 

2.

 

3.

 

4.

Solving Equations Involving Roots and Exponents

The goal of solving equations involving exponents is to remove the exponent from the variable. This is accomplished by taking the corresponding root of both sides. For example, if we are removing an exponent two (square), we take the square root. If we are removing an exponent five, we take the fifth root, and so on.

Example:

Solve the equation for c:

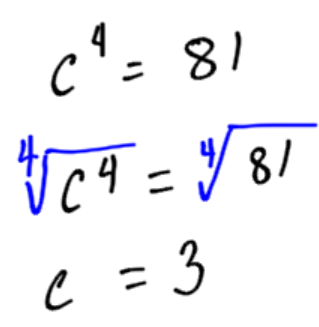
Or

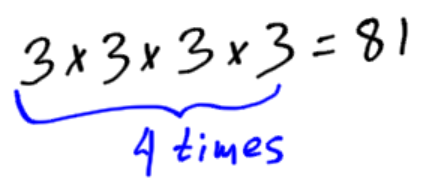
In the previous example, we can just think of a number that, when multiplied by itself four times, equals 81. In other cases, we must use our calculators to approximate an answer.

Example:

Solve the equation for w:

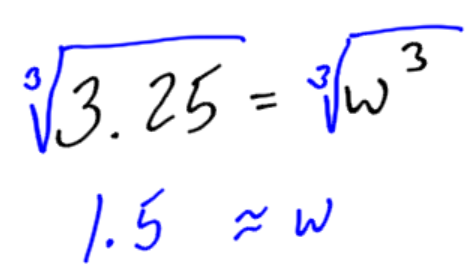
When there is a root in the equation, we can remove it by exponentiating both sides.

Example:

Solve the equation for v:

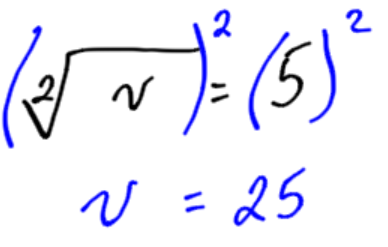
Practice Exercises: Solving Equations with Roots and Exponents

1. Find the variable in each quadratic or cubic equation.

a. 

b. 

c. 

d. 

2. Find the variable in each square root equation.

a.

b.

c.

d.

3. Find the variable in each cube root equation

a.

b.

c.

d.

Answer Key

1. 1, 12, 13, 20

2. 196, 25, 1, 144

3. 1, 343, 8000, 729

Topic 7: Solving Multi-Step Equations

Up until this point, all the equations we have solved have involved only one operation to isolate the variable. In some cases, there will be many steps involved before the variable is alone. There are some rules to follow, and a general strategy you can use. The tricky part is sometimes you don’t know where to start. The good part is that if you follow the rules, any step you take won’t be wrong, it just might not bring you closer to the solution.

The Goal

The goal, or objective, of solving any equation is to get the variable “isolated” (on one side of the equals sign, alone.) Note that the variable cannot have a negative sign, or exponent either.

The Rule

The one an only rule is the golden rule: “Do unto one side, as thou doest unto the other.” This rule is biblical in proportion. If you do something to one side of the equation you must do the same thing to the other to keep things in balance.

The Steps

As we discussed in the previous sections, you can take the following steps:

• If there is a number added, you can subtract it (or add the negative) from both sides. Alternatively, if there is a negative number, you can pair it off with a positive.
• If there is a number multiplied to the variable, you can multiply by the reciprocal (or divide) from both sides. If there is a number that divides the variable, you can multiply it to both sides.
• If there is an exponent, you can take the square root of both sides. If there is a square root, you can exponentiate both sides.

A Strategy

You can follow the above steps in any order, but in general, if there is adding (or subtracting) and multiplication (or division) in an equation, do the adding (or subtracting) first and then the multiplication (or division).

Example:

Solve the equation for x:

Mathematical Step	What I’m Thinking
	There are 2 things preventing x from being on one side alone. It is multiplied by 5 (so I am going to use multiply the reciprocal) and it has 3 added to it (so I am going to use a negative 3)
	As the above strategy suggests, use a negative 3 to get rid of the three first.
	Now that the 5x is on one side alone, multiply by the reciprocal.

Practice Exercises: Solving Multi-Step Equations

1)

 

2) 

 

3) 

 

4) 

 

Answer Key

1.-13/3 or -4.3, 2. 10/3 or 3.3, 3. -4/6 or -0.7, 4. -7/3 or -2.3

Topic 8: Combining Equations using Variable Substitutions

In some cases, it will be necessary to combine two equations to solve a problem.

Example:

The cross sectional area of a cylindrical pole is a circle. The area of this cross sectional circle is given by the formula:

The radius of a pole changes depending where on the pole it is measured. At the butt, the radius is the largest, at 14 inches. At the snipe, the radius is slightly smaller, at 8.5 inches. The equation for the radius of the pole in inches is:

Where r is the radius of the pole in inches, and l is the length from the butt in feet.

Find the cross sectional area of the pole at a distance of 6 feet from the butt.

This is a two-step process:

• Find the radius of the pole with the second equation, given the length of 6 feet.
• Us the radius found in step one to find the cross sectional area (using the first equation.)

Step 1:

The radius at length 6 feet from the butt is calculated like this:

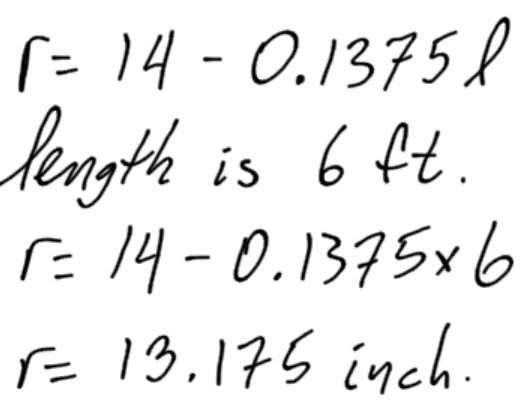
The radius at 6 feet is 13.175 inches.

Step 2:

The cross sectional area of the pole at 6 feet, where the radius is 13.175 inches, is calculated like this:

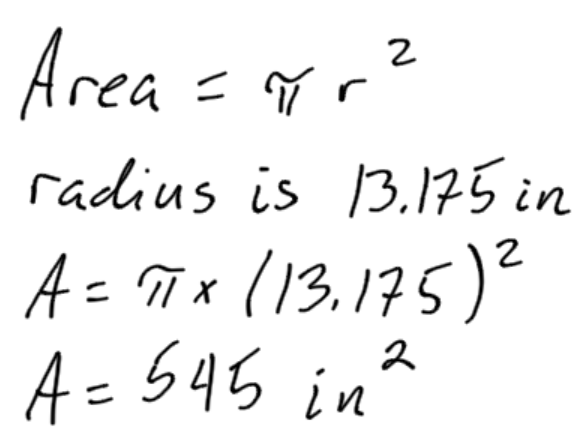
The cross sectional area of a pole at a distance of 6 feet from the but is roughly 545 inches squared.

There is an easier way to do this if we need to do the same calculation over and over again. We can take the two equations and combine them to make one. We do this using algebra.

Instead of taking the number for radius that we calculated in equation 2 and substituting it into equation 1, we can take the whole expression and substitute it into equation1.

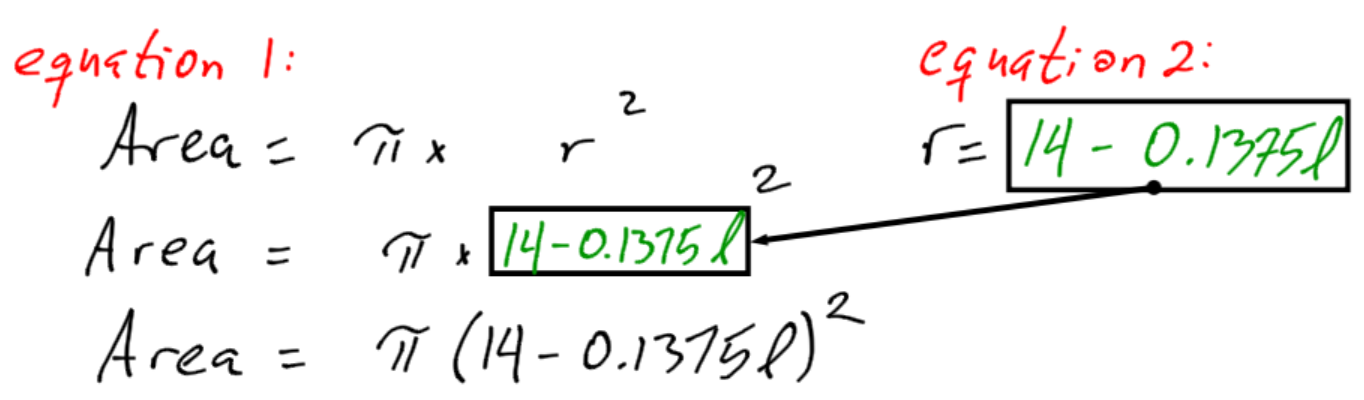
Now we have one equation. If we know the length from the butt, we can calculate the cross sectional area directly:

To test the equation, let’s try it for a length of 6 feet. From our calculations above, we know the cross sectional area at 6 feet should be 545 square inches.

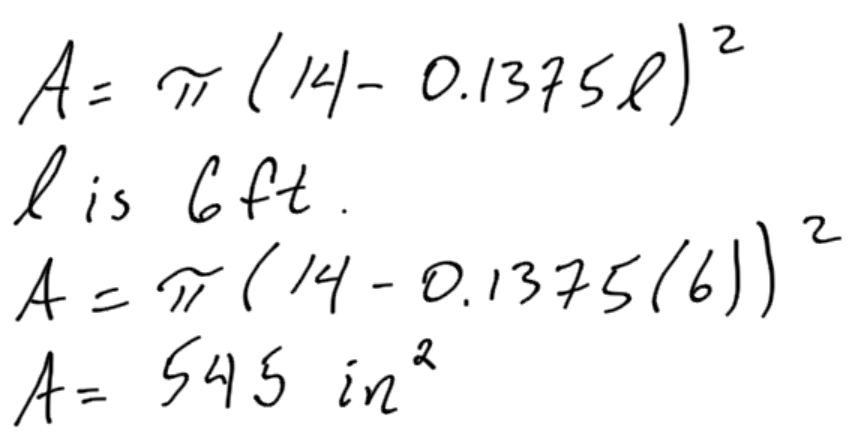
We arrive at the same conclusion using our new formula: the cross sectional area at 6 feet from the butt is 545 square inches.

Practice Exercises: Combining Equations using Variable Substitutions

1. There was a vehicle crash which may have involved high speed. The investigator is trying to determine how fast the vehicle was moving.The velocity of the vehicle can be determined by the equation:

where the variable, v is velocity, and t is the time the object has been traveling.

The investigator doesn’t know how much time the vehicle spent traveling, but the tracks were measured to be 537 m. The amount of time the object travelled based on distance is given by the equation:

where t is the amount of time the object has been traveling and x is the distance traveled.

a) Combine equation 1 and 2 to form one equation that gives the velocity of the vehicle given the distance it travelled.

b) Calculate the velocity of the vehicle using the combined formula. The distance, x, is 189 m.

Answer key

1a. .  This can be simiplified to .

1b. v = 30 m/s (or 108 km/hr)