46 Outcome 1: Linear Mechanics

The information in this outcome is provided from the open source textbook: Gozuacik, Pattison, Tabor: “Physics.” March 26, 2020. Openstax.org. Accessed on “https://openstax.org/details/books/physics” on August 9, 2021. This material is used under the Creative Commons Attribution License V4.0.

Outcome/Competency: You will be able to describe and predict outcomes of systems using Newton’s Laws.

Rationale:
Why is it important for you to learn this skill?

Our understanding of the way things move, and how force interacts with matter, stems from three observations recorded by Isaac Newton. Understanding Newton’s Laws lets us be able to predict what will happen if a force is applied. Whether you drop a tool, or lift a transformer with a sling, you will be able to predict the nature of the motion and force required.

Objectives:

To be competent in this area, the individual must be able to:

• Apply basic terms and calculations used in the study of Newton’s laws

Learning Goals

• Define terms and perform calculations related to Newton’s laws
• Solve problems using analytical vector methods.

Introduction:

In this section you will explore the use of linear mechanics and Newton’s Laws. You will learn how to calculate and define terms related to linear motion, the applications of kinematic formulations, and how to problem solve using graphics, trigonometry, and vectors. You will be presented with content, participate in group discussions go through examples and be given opportunities to practice throughout. There will be a test at the end of each topic.

Mechanics is a branch of physics that deals with forces and the effect of forces on objects. There are two branches of mechanics: statics and dynamics. Statics deals with forces on objects that aren’t moving: all forces are in balance. Dynamics deals with effects of force on objects that are in motion. We will learn about statics in this course because it applies directly to the power line trade.

Topic 1: Newton’s Laws (3h)

Figure 1 Newton’s laws of motion describe the motion of the dolphin’s path. (Credit: Jin Jang)

Isaac Newton (1642–1727) was a natural philosopher; a great thinker who combined science and philosophy to try to explain the workings of nature on Earth and in the universe. His laws of motion were just one part of the monumental work that has made him legendary. The development of Newton’s laws marks the transition from the Renaissance period of history to the modern era. This transition was characterized by a revolutionary change in the way people thought about the physical universe. Drawing upon earlier work by scientists Galileo Galilei and Johannes Kepler, Newton’s laws of motion allowed motion on Earth and in space to be predicted mathematically. In this chapter you will learn about force as well as Newton’s first, second, and third laws of motion.

Introduction to Newton’s Laws

By the end of this section, you will be able to do the following:

• Differentiate between internal force and external force
• Draw a free-body diagram
• Calculate force required for lifts

Section Key Terms

• external force
• force
• free-body diagram
• net external force
• net force

Defining Force and Dynamics

A force pushes or pulls an object. The object being moved by a force could be an inanimate object, a table, or an animate object, a person. The pushing or pulling may be done by a person, or even the gravitational pull of Earth. Forces have different magnitudes and directions; this means that some forces are stronger than others and can act in different directions. For example, a cannon exerts a strong force on the cannonball that is launched into the air. In contrast, a mosquito landing on your arm exerts only a small force on your arm.

When multiple forces act on an object, the forces combine. Adding together all the forces acting on an object gives the total force, or net force. An external force is a force that acts on an object within the system from outside the system. This type of force is different than an internal force, which acts between two objects that are both within the system. The net external force combines these two definitions; it is the total combined external force. We discuss further details about net force, external force, and net external force in the coming sections.

In mathematical terms, two forces acting in opposite directions have opposite signs (positive or negative). By convention, the negative sign is assigned to any movement to the left or downward. If two forces pushing in opposite directions are added together, the larger force will be somewhat canceled out by the smaller force pushing in the opposite direction. It is important to be consistent with your chosen coordinate system within a problem; for example, if negative values are assigned to the downward direction for velocity, then distance, force, and acceleration should also be designated as being negative in the downward direction.

Free-Body Diagrams and Examples of Forces

For our first example of force, consider an object hanging from a rope. This example gives us the opportunity to introduce a useful tool known as a free-body diagram. A free-body diagram represents the object being acted upon—that is, the free body—as a single point. Only the forces acting on the body (that is, external forces) are shown and are represented by vectors (which are drawn as arrows). These forces are the only ones shown because only external forces acting on the body affect its motion. We can ignore any internal forces within the body because they cancel each other out, as explained in the section on Newton’s third law of motion. Free-body diagrams are very useful for analyzing forces acting on an object.

Figure 2 An object of mass, m, is held up by the force of tension.

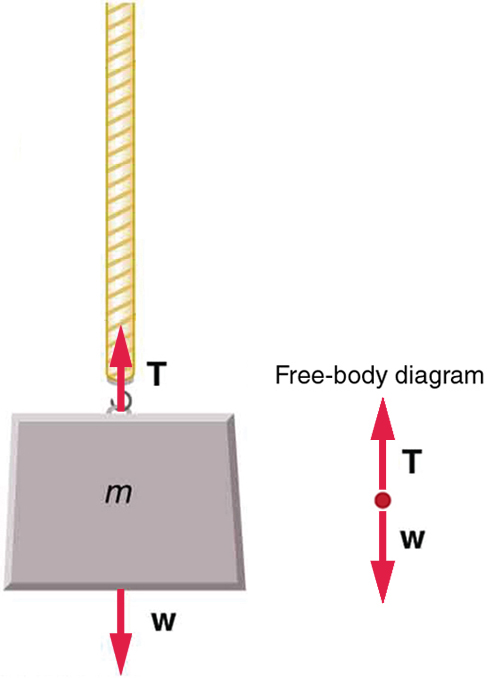
Figure 2 shows the force of tension in the rope acting in the upward direction, opposite the force of gravity. The forces are indicated in the free-body diagram by an arrow pointing up, representing tension, and another arrow pointing down, representing gravity. In a free-body diagram, the lengths of the arrows show the relative magnitude (or strength) of the forces. Because forces are vectors, they add just like other vectors. Notice that the two arrows have equal lengths in Figure 2, which means that the forces of tension and weight are of equal magnitude. Because these forces of equal magnitude act in opposite directions, they are perfectly balanced, so they add together to give a net force of zero.

Not all forces are as noticeable as when you push or pull on an object. Some forces act without physical contact, such as the pull of a magnet (in the case of magnetic force) or the gravitational pull of Earth (in the case of gravitational force).

In the next three sections discussing Newton’s laws of motion, we will learn about three specific types of forces: friction, the normal force, and the gravitational force. To analyze situations involving forces, we will create free-body diagrams to organize the framework of the mathematics for each individual situation.

Tips for Success

Correctly drawing and labeling a free-body diagram is an important first step for solving a problem. It will help you visualize the problem and correctly apply the mathematics to solve the problem.

Review Questions

 

[h5p id=”2″]

Newton’s First Law of Motion: Inertia

By the end of this section, you will be able to do the following:

• Describe Newton’s first law and friction, and
• Discuss the relationship between mass and inertia.

Section Key Terms

friction

coefficient of friction

normal force

inertia

law of inertia

mass

Newton’s first law of motion

system

Newton’s first law of motion states the following:

• A body at rest tends to remain at rest.
• A body in motion tends to remain in motion at a constant velocity unless acted on by a net external force. (Recall that constant velocity means that the body moves in a straight line and at a constant speed.)

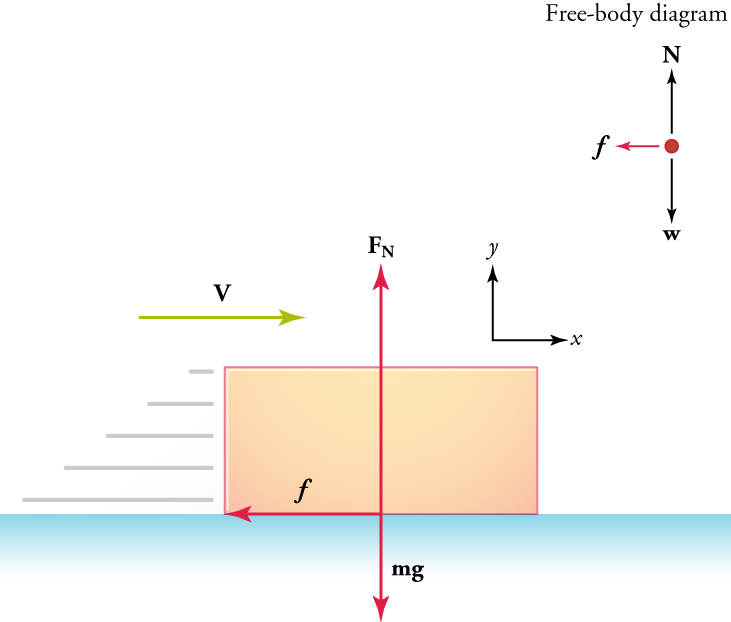
Figure 3 For a box sliding across a floor, friction acts in the direction opposite to the velocity.

At first glance, this law may seem to contradict your everyday experience. You have probably noticed that a moving object will usually slow down and stop unless some effort is made to keep it moving. The key to understanding why, for example, a sliding box slows down (seemingly on its own) is to first understand that a net external force acts on the box to make the box slow down. Without this net external force, the box would continue to slide at a constant velocity (as stated in Newton’s first law of motion). What force acts on the box to slow it down? This force is called friction. Friction is an external force that acts opposite to the direction of motion (see Figure 3). Think of friction as a resistance to motion that slows things down.

Consider an air hockey table. When the air is turned off, the puck slides only a short distance before friction slows it to a stop. However, when the air is turned on, it lifts the puck slightly, so the puck experiences very little friction as it moves over the surface. With friction almost eliminated, the puck glides along with very little change in speed. On a frictionless surface, the puck would experience no net external force (ignoring air resistance, which is also a form of friction). Additionally, if we know enough about friction, we can accurately predict how quickly objects will slow down.

Now let’s think about another example. A man pushes a box across a floor at constant velocity by applying a force of +50 N. (The positive sign indicates that, by convention, the direction of motion is to the right.) What is the force of friction that opposes the motion? The force of friction must be −50 N. Why? According to Newton’s first law of motion, any object moving at constant velocity has no net external force acting upon it, which means that the sum of the forces acting on the object must be zero. The mathematical way to say that no net external force acts on an object is F_net= 0 or ΣF=0. So, if the man applies +50 N of force, then the force of friction must be −50 N for the two forces to add up to zero (that is, for the two forces to cancel each other). Whenever you encounter the phrase at constant velocity, Newton’s first law tells you that the net external force is zero.

The force of friction depends on two factors: the coefficient of friction and the normal force. For any two surfaces that are in contact with one another, the coefficient of friction is a constant that depends on the nature of the surfaces. The normal force is the force exerted by a surface that pushes on an object in response to gravity pulling the object down. In equation form, the force of friction is:

F_f=μN

where μ is the coefficient of friction and N is the normal force. (The coefficient of friction is discussed in more detail in another chapter, and the normal force is discussed in more detail in the section Newton’s Third Law of Motion.)

Recall from the section on Force that a net external force acts from outside on the object of interest. A more precise definition is that it acts on the system of interest. A system is one or more objects that you choose to study. It is important to define the system at the beginning of a problem to figure out which forces are external and need to be considered, and which are internal and can be ignored.

For example, in Figure 4 (a), two children push a third child in a wagon at a constant velocity. The system of interest is the wagon plus the small child, as shown in part (b) of the figure. The two children behind the wagon exert external forces on this system (F₁, F₂). Friction f acting at the axles of the wheels and at the surface where the wheels touch the ground two other external forces acting on the system. Two more external forces act on the system: the weight W of the system pulling down and the normal force N of the ground pushing up. Notice that the wagon is not accelerating vertically, so Newton’s first law tells us that the normal force balances the weight. Because the wagon is moving forward at a constant velocity, the force of friction must have the same strength as the sum of the forces applied by the two children.

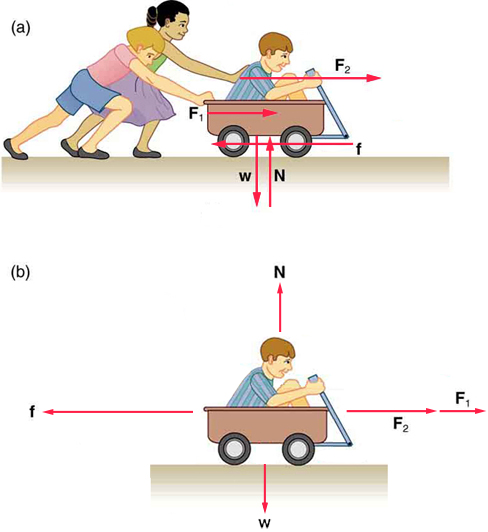
Figure 4 Forces acting on wagon.

(a) The wagon and rider form a system that is acted on by external forces.

(b) The two children pushing the wagon and child provide two external forces. Friction acting at the wheel axles and on the surface of the tires where they touch the ground provide an external force that act against the direction of motion. The weight W and the normal force N from the ground are two more external forces acting on the system. All external forces are represented in the figure by arrows. All the external forces acting on the system add together, but because the wagon moves at a constant velocity, all of the forces must add up to zero.

Mass and Inertia

Inertia is the tendency for an object at rest to remain at rest, or for a moving object to remain in motion in a straight line with constant speed. This key property of objects was first described by Galileo. Later, Newton incorporated the concept of inertia into his first law, which is often referred to as the law of inertia.

As we know from experience, some objects have more inertia than others. For example, changing the motion of a large truck is more difficult than changing the motion of a toy truck. In fact, the inertia of an object is proportional to the mass of the object. Mass is a measure of the amount of matter (or stuff) in an object. The quantity or amount of matter in an object is determined by the number and types of atoms the object contains. Unlike weight (which changes if the gravitational force changes), mass does not depend on gravity. The mass of an object is the same on Earth, in orbit, or on the surface of the moon. In practice, it is very difficult to count and identify all the atoms and molecules in an object, so mass is usually not determined this way. Instead, the mass of an object is determined by comparing it with the standard kilogram. Mass is therefore expressed in kilograms.

Tips For Success

In everyday language, people often use the terms weight and mass interchangeably—but this is not correct. Weight is a force. (We cover this topic in more detail in the section Newton’s Second Law of Motion.)

 

[h5p id=”3″]

Newton’s Second Law of Motion

By the end of this section, you will be able to do the following:

• Describe Newton’s second law, both verbally and mathematically
• Use Newton’s second law to solve problems

Section Key Terms

freefall

Newton’s second law of motion

weight

Describing Newton’s Second Law of Motion

Newton’s first law considered bodies at rest or bodies in motion at a constant velocity. The other state of motion to consider is when an object is moving with a changing velocity, which means a change in the speed and/or the direction of motion. This type of motion is addressed by Newton’s second law of motion, which states how force causes changes in motion. Newton’s second law of motion is used to calculate what happens in situations involving forces and motion, and it shows the mathematical relationship between force, mass, and acceleration. Mathematically, the second law is most often written as

Fnet=m×a

or

∑F=ma

where F_net (or ∑F) is the net external force, m is the mass of the system, and a is the acceleration. Note that F_net and ∑F are the same because the net external force is the sum of all the external forces acting on the system.

First, what do we mean by a change in motion? A change in motion is simply a change in velocity: the speed of an object can become slower or faster, the direction in which the object is moving can change, or both variables may change. A change in velocity means, by definition, that an acceleration has occurred. Newton’s first law says that only a nonzero net external force can cause a change in motion, so a net external force must cause an acceleration. Note that acceleration can refer to slowing down or to speeding up. Acceleration can also refer to a change in the direction of motion with no change in speed because acceleration is the change in velocity divided by the time it takes for that change to occur, and velocity is defined by speed and direction.

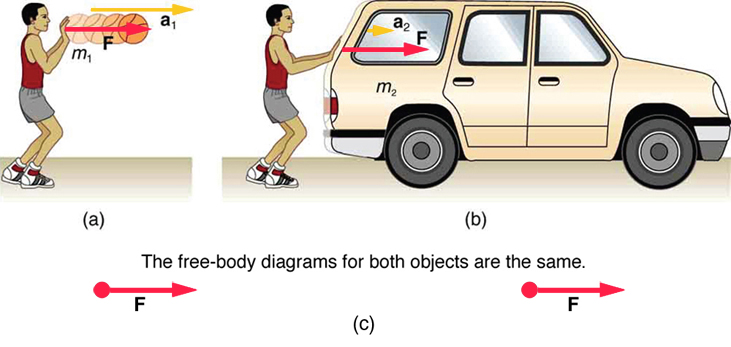
Figure 5

In Figure 5, the same force exerted on systems of different masses produces different accelerations. (a) A boy pushes a basketball to make a pass. The effect of gravity on the ball is ignored. (b) The same boy pushing with identical force on a stalled car produces a far smaller acceleration (friction is negligible). Note that the free-body diagrams for the ball and for the car are identical, which allows us to compare the two situations.

Applying Newton’s Second Law

Before putting Newton’s second law into action, it is important to consider units. The equation F_net=ma is used to define the units of force in terms of the three basic units of mass, length, and time (recall that acceleration has units of length divided by time squared). The SI unit of force is called the newton (abbreviated N) and is the force needed to accelerate a 1-kg system at the rate of 1 m/s². That is, because F_net=ma, we have

1N=kg×ms2

One of the most important applications of Newton’s second law is to calculate weight (also known as the gravitational force), which is usually represented mathematically as W. When people talk about gravity, they don’t always realize that it is an acceleration. When an object is dropped, it accelerates toward the center of Earth. Newton’s second law states that the net external force acting on an object is responsible for the acceleration of the object. If air resistance is negligible, the net external force on a falling object is only the gravitational force (i.e., the weight of the object).

Weight can be represented by a vector because it has a direction. Down is defined as the direction in which gravity pulls, so weight is normally considered a downward force. By using Newton’s second law, we can figure out the equation for weight.

Consider an object with mass m falling toward Earth. It experiences only the force of gravity (i.e., the gravitational force or weight), which is represented by W. Newton’s second law states that F_net=ma. Because the only force acting on the object is the gravitational force, we have F_net =W. We know that the acceleration of an object due to gravity is g, so we have a=g. Substituting these two expressions into Newton’s second law gives

W=mg

This is the equation for weight—the gravitational force on a mass m. On Earth, g = 9.80 m/s², so the weight (disregarding for now the direction of the weight) of a 1.0-kg object on Earth is

W=m×g=(1.0kg)×(9.80ms2)=9.8N

Although most of the world uses newtons as the unit of force, in the United States the most familiar unit of force is the pound (lb), where 1 N = 0.225 lb.

When the net external force on an object is its weight, we say that it is in freefall. In this case, the only force acting on the object is the force of gravity. On the surface of Earth, when objects fall downward toward Earth, they are never truly in freefall because there is always some upward force due to air resistance that acts on the object (and there is also the buoyancy force of air, which is like the buoyancy force in water that keeps boats afloat).

Gravity varies slightly over the surface of Earth, so the weight of an object depends very slightly on its location on Earth. Weight varies dramatically away from Earth’s surface. On the moon, for example, the acceleration due to gravity is only 1.67 m/s². Because weight depends on the force of gravity, a 1.0-kg mass weighs 9.8 N on Earth and only about 1.7 N on the moon.

It is important to remember that weight and mass are very different, although they are closely related. Mass is the quantity of matter (how much stuff) in an object and does not vary, but weight is the gravitational force on an object and is proportional to the force of gravity. It is easy to confuse the two, because our experience is confined to Earth, and the weight of an object is essentially the same no matter where you are on Earth. Adding to the confusion, the terms mass and weight are often used interchangeably in everyday language; for example, our medical records often show our weight in kilograms, but never in the correct unit of newtons.

[h5p id=”4″]

Worked Example

What Acceleration Can a Person Produce when Pushing a Lawn Mower?

Suppose that the net external force (push minus friction) exerted on a lawn mower is 51 N parallel to the ground. The mass of the mower is 240 kg. What is its acceleration?

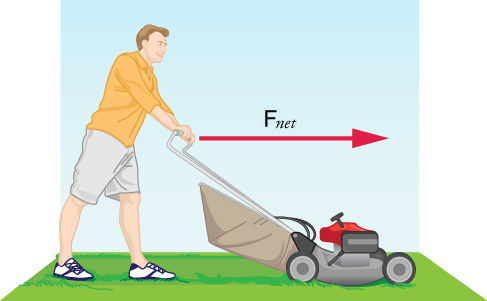
Strategy

Because F_net and m are given, the acceleration can be calculated directly from Newton’s second law: F_net = ma.

Solution

Solving Newton’s second law for the acceleration, we find that the magnitude of the acceleration, a, is a= F_net / m. Entering the given values for net external force and mass gives:

a=51N240kg

Inserting the units kg⋅m/s² for N yields

a=51kg∙ms2÷240kg=0.21ms2

Practice Exercises

[h5p id=”5″]

Newton’s Third Law of Motion

Section Learning Objectives

By the end of this section, you will be able to do the following:

• Describe Newton’s third law, both verbally and mathematically
• Use Newton’s third law to solve problems

Section Key Terms

Newton’s third law of motion

normal force

tension

thrust

Describing Newton’s Third Law of Motion

If you have ever stubbed your toe, you have noticed that although your toe initiates the impact, the surface that you stub it on exerts a force back on your toe. Although the first thought that crosses your mind is probably “ouch, that hurt” rather than “this is a great example of Newton’s third law,” both statements are true.

This is exactly what happens whenever one object exerts a force on another—each object experiences a force that is the same strength as the force acting on the other object but that acts in the opposite direction. Everyday experiences, such as stubbing a toe or throwing a ball, are all perfect examples of Newton’s third law in action.

Newton’s third law of motion states that whenever a first object exerts a force on a second object, the first object experiences a force equal in magnitude but opposite in direction to the force that it exerts.

Newton’s third law of motion tells us that forces always occur in pairs, and one object cannot exert a force on another without experiencing the same strength force in return. We sometimes refer to these force pairs as action-reaction pairs, where the force exerted is the action, and the force experienced in return is the reaction (although which is which depends on your point of view).

Newton’s third law is useful for figuring out which forces are external to a system. Recall that identifying external forces is important when setting up a problem, because the external forces must be added together to find the net force.

We can see Newton’s third law at work by looking at how people move about. Consider a swimmer pushing off from the side of a pool, as illustrated in Figure 6. She pushes against the pool wall with her feet and accelerates in the direction opposite to her push. The wall has thus exerted on the swimmer a force of equal magnitude but in the direction opposite that of her push. You might think that two forces of equal magnitude but that act in opposite directions would cancel, but they do not because they act on different systems.

In this case, there are two different systems that we could choose to investigate: the swimmer or the wall. If we choose the swimmer to be the system of interest, as in the figure, then F_wall on feet is an external force on the swimmer and affects her motion. Because acceleration is in the same direction as the net external force, the swimmer moves in the direction of F_{wall on feet}. Because the swimmer is our system (or object of interest) and not the wall, we do not need to consider the force F_{feet on wall} because it originates from the swimmer rather than acting on the swimmer. Therefore, F_{feet on wall} does not directly affect the motion of the system and does not cancel F_{wall on feet}. Note that the swimmer pushes in the direction opposite to the direction in which she wants to move.

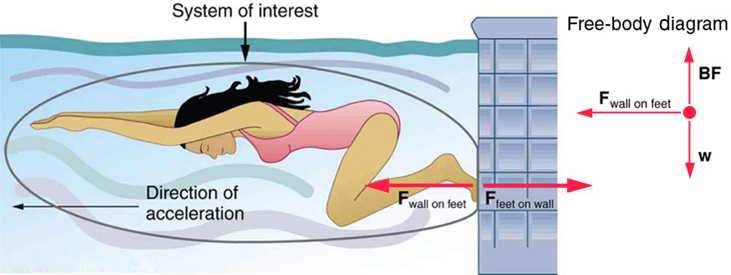
Figure 6

When the swimmer exerts a force F_{feet on wall} on the wall, she accelerates in the direction opposite to that of her push. This means that the net external force on her is in the direction opposite to F_{feet on wall}. This opposition is the result of Newton’s third law of motion, which dictates that the wall exerts a force F_{wall on feet} on the swimmer that is equal in magnitude but that acts in the direction opposite to the force that the swimmer exerts on the wall.

Other examples of Newton’s third law are easy to find. As a teacher paces in front of a whiteboard, he exerts a force backward on the floor. The floor exerts a reaction force in the forward direction on the teacher that causes him to accelerate forward. Similarly, a car accelerates because the ground pushes forward on the car’s wheels in reaction to the car’s wheels pushing backward on the ground. You can see evidence of the wheels pushing backward when tires spin on a gravel road and throw rocks backward.

Another example is the force of a baseball as it makes contact with the bat. Helicopters create lift by pushing air down, creating an upward reaction force. Birds fly by exerting force on air in the direction opposite that in which they wish to fly. For example, the wings of a bird force air downward and backward in order to get lift and move forward. An octopus propels itself forward in the water by ejecting water backward through a funnel in its body, which is similar to how a jet ski is propelled. In these examples, the octopus or jet ski push the water backward, and the water, in turn, pushes the octopus or jet ski forward.

Applying Newton’s Third Law

Forces are classified and given names based on their source, how they are transmitted, or their effects. In previous sections, we discussed the forces called push, weight, and friction. In this section, applying Newton’s third law of motion will allow us to explore three more forces: the normal force, tension, and thrust. However, because we haven’t yet covered vectors in depth, we’ll only consider one-dimensional situations in this chapter.

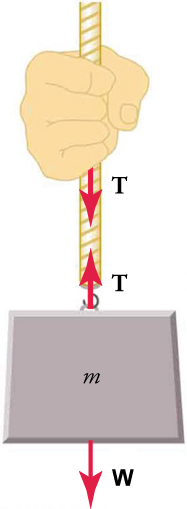
Figure 7

The gravitational force (or weight) acts on objects at all times and everywhere on Earth. We know from Newton’s second law that a net force produces an acceleration; so, why is everything not in a constant state of freefall toward the center of Earth? The answer is the normal force. The normal force is the force that a surface applies to an object to support the weight of that object; it acts perpendicular to the surface upon which the object rests. If an object on a flat surface is not accelerating, the net external force is zero, and the normal force has the same magnitude as the weight of the system but acts in the opposite direction. In equation form, we write that

Note that this equation is only true for a horizontal surface.

Tension

The word tension comes from the Latin word meaning to stretch. Tension is the force along the length of a flexible connector, such as a string, rope, chain, or cable. Regardless of the type of connector attached to the object of interest, one must remember that the connector can only pull (or exert tension) in the direction parallel to its length. Tension is a pull that acts parallel to the connector, and that acts in opposite directions at the two ends of the connector. This is possible because a flexible connector is simply a long series of action-reaction forces, except at the two ends where outside objects provide one member of the action-reaction forces.

Consider a person holding a mass on a rope, as shown in figure 7

When a perfectly flexible connector (one requiring no force to bend it) such as a rope transmits a force T, this force must be parallel to the length of the rope, as shown. The pull that such a flexible connector exerts is a tension. Note that the rope pulls with equal magnitude force but in opposite directions to the hand and to the mass (neglecting the weight of the rope). This is an example of Newton’s third law. The rope is the medium that transmits forces of equal magnitude between the two objects but that act in opposite directions.

Tension in the rope must equal the weight of the supported mass, as we can prove by using Newton’s second law. If the 5.00 kg mass in the figure is stationary, then its acceleration is zero, so F_net=0. The only external forces acting on the mass are its weight W and the tension T supplied by the rope. Summing the external forces to find the net force, we obtain

where T and W are the magnitudes of the tension and weight, respectively, and their signs indicate direction, with up being positive. By substituting mg for F_net and rearranging the equation, the tension equals the weight of the supported mass, just as you would expect.

For a 5.00-kg mass (neglecting the mass of the rope), we see that

Another example of Newton’s third law in action is thrust. Rockets move forward by expelling gas backward at a high velocity. This means that the rocket exerts a large force backward on the gas in the rocket combustion chamber, and the gas, in turn, exerts a large force forward on the rocket in response. This reaction force is called thrust.

Figure 8

Tips for Success

The basics of problem solving, presented earlier in this text, are followed here with specific strategies for applying Newton’s laws of motion. These techniques also reinforce concepts that are useful in many other areas of physics.

First, identify the physical principles involved. If the problem involves forces, then Newton’s laws of motion are involved, and it is important to draw a careful sketch of the situation. An example of a sketch is shown in Figure 8. Next, as in Figure 8, use vectors to represent all forces. Label the forces carefully, and make sure that their lengths are proportional to the magnitude of the forces and that the arrows point in the direction in which the forces act.

(a) A picture of a crane lifting a container (figure 8).

Figure 9 Vector representation of force

(b) Arrows are used to represent all forces. T is the tension exerted on the container by the chain, F_T is the force exerted on the chain by the container, and W is the containers weight (i.e., the force exerted on the container by Earth’s gravity). All other forces such as wind, are assumed to be negligible.

Suppose we are given the container’s mass and asked to find the tension in the chain. We define the system of interest as shown and draw a free-body diagram, as shown in (c). F_T is no longer shown because it does not act on the system of interest; rather, F_T acts on the outside world.

(c) The free-body diagram shows only the external forces acting on the container. For these to sum to zero, we must have T=W.

Next, make a list of knowns and unknowns and assign variable names to the quantities given in the problem. Figure out which variables need to be calculated; these are the unknowns. Now carefully define the system: which objects are of interest for the problem. This decision is important, because Newton’s second law involves only external forces. Once the system is identified, it’s possible to see which forces are external and which are internal (see Figure 8).

If the system acts on an object outside the system, then you know that the outside object exerts a force of equal magnitude but in the opposite direction on the system.

A diagram showing the system of interest and all the external forces acting on it is called a free-body diagram. Only external forces are shown on free-body diagrams, not acceleration or velocity. Figure 8 shows a free-body diagram for the system of interest.

After drawing a free-body diagram, apply Newton’s second law to solve the problem. This is done in Figure 8 for the case of the container hanging from a sling. When external forces are clearly identified in the free-body diagram, translate the forces into equation form and solve for the unknowns. Note that forces acting in opposite directions have opposite signs. By convention, forces acting downward or to the left are usually negative.

[h5p id=”7″]

 

[h5p id=”6″]

 

Worked Example

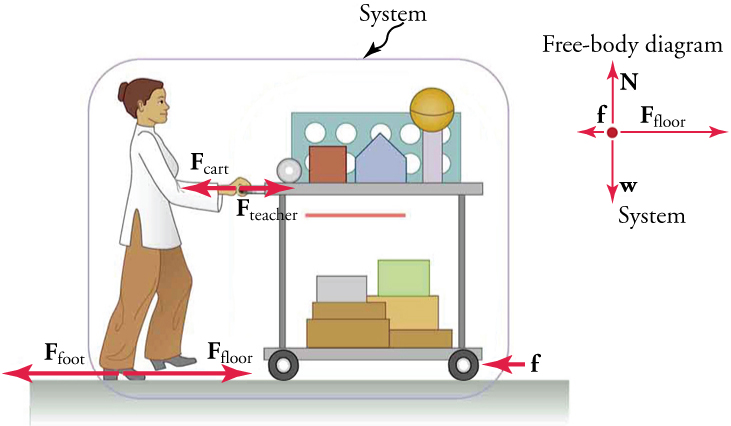
Figure 10 An Accelerating Equipment Cart

A physics teacher pushes a cart of demonstration equipment to a classroom, as in Figure 9. Her mass is 65.0 kg, the cart’s mass is 12.0 kg, and the equipment’s mass is 7.0 kg. To push the cart forward, the teacher’s foot applies a force of 150 N in the opposite direction (backward) on the floor. Calculate the acceleration produced by the teacher. The force of friction, which opposes the motion, is 24.0 N.

STRATEGY

Because they accelerate together, we define the system to be the teacher, the cart, and the equipment. The teacher pushes backward with a force F_foot of 150 N. According to Newton’s third law, the floor exerts a forward force F_floor of 150 N on the system. Because all motion is horizontal, we can assume that no net force acts in the vertical direction, and the problem becomes one dimensional. As noted in the figure, the friction f opposes the motion and therefore acts opposite the direction of F_floor.

We should not include the forces F_teacher , F_cart , or F_foot because these are exerted by the system, not on the system. We find the net external force by adding together the external forces acting on the system (see the free-body diagram in the figure) and then use Newton’s second law to find the acceleration.

Solution

Newton’s second law is

The net external force on the system is the sum of the external forces: the force of the floor acting on the teacher, car, and equipment (in the horizontal direction) and the force of friction. Because friction acts in the opposite direction, we assign it a negative value. This, for the net force, we obtain

The mass of the system is the sum of the mass of the teacher, cart, and equipment.

Insert these values of Fnet and m into Newton’s second law to obtain the acceleration of the system,

F₁ < F₂

Discussion

None of the forces between components of the system, such as between the teacher’s hands and the cart, contribute to the net external force because they are internal to the system. Another way to look at this is to note that the forces between components of a system cancel because they are equal in magnitude and opposite in direction. For example, the force exerted by the teacher on the cart is of equal magnitude but in the opposite direction of the force exerted by the cart on the teacher. In this case, both forces act on the same system, so they cancel. Defining the system was crucial to solving this problem.

 

[h5p id=”8″]

Key Terms

Dynamics– the study of how forces affect the motion of objects and systems

external force– a force acting on an object or system that originates outside of the object or system

force– a push or pull on an object with a specific magnitude and direction; can be represented by vectors; can be expressed as a multiple of a standard force

free-body diagram– a diagram showing all external forces acting on a body

freefall– a situation in which the only force acting on an object is the force of gravity

friction– an external force that acts in the direction opposite to the direction of motion

inertia– the tendency of an object at rest to remain at rest, or for a moving object to remain in motion in a straight line and at a constant speed

law of inertia– Newton’s first law of motion: a body at rest remains at rest or, if in motion, remains in motion at a constant speed in a straight line, unless acted on by a net external force; also known as the law of inertia

Mass– the quantity of matter in a substance; measured in kilograms

net external force– the sum of all external forces acting on an object or system

net force– the sum of all forces acting on an object or system

Newton’s first law of motion– a body at rest remains at rest or, if in motion, remains in motion at a constant speed in a straight line, unless acted on by a net external force; also known as the law of inertia

Newton’s second law of motion- the net external force, F_net, on an object is proportional to and in the same direction as the acceleration of the object, a, and also proportional to the object’s mass, m; defined mathematically as F_net=ma or ΣF=ma.

Newton’s third law of motion- when one body exerts a force on a second body, the first body experiences a force that is equal in magnitude and opposite in direction to the force that it exerts

normal force- the force that a surface applies to an object; acts perpendicular and away from the surface with which the object is in contact

system- one or more objects of interest for which only the forces acting on them from the outside are considered, but not the forces acting between them or inside them

 

tension- a pulling force that acts along a connecting medium, especially a stretched flexible connector, such as a rope or cable; when a rope supports the weight of an object, the force exerted on the object by the rope is called tension

thrust- a force that pushes an object forward in response to the backward ejection of mass by the object; rockets and airplanes are pushed forward by a thrust reaction force in response to ejecting gases backward

weight- the force of gravity, W, acting on an object of mass m; defined mathematically as W = mg, where g is the magnitude and direction of the acceleration due to gravity

Section Summary

Force

Dynamics is the study of how forces affect the motion of objects and systems.

Force is a push or pull that can be defined in terms of various standards. It is a vector and so has both magnitude and direction.

External forces are any forces outside of a body that act on the body. A free-body diagram is a drawing of all external forces acting on a body.

Newton’s First Law of Motion: Inertia

Newton’s first law states that a body at rest remains at rest or, if moving, remains in motion in a straight line at a constant speed, unless acted on by a net external force. This law is also known as the law of inertia.

Inertia is the tendency of an object at rest to remain at rest or, if moving, to remain in motion at constant velocity. Inertia is related to an object’s mass.

Friction is a force that opposes motion and causes an object or system to slow down.

Mass is the quantity of matter in a substance.

Newton’s Second Law of Motion

Acceleration is a change in velocity, meaning a change in speed, direction, or both.

An external force acts on a system from outside the system, as opposed to internal forces, which act between components within the system.

Newton’s second law of motion states that the acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system, and inversely proportional to the system’s mass.

In equation form, Newton’s second law of motion is F_net=ma or ΣF=ma. This is sometimes written as a=F_net/m or a=ΣF/m.

The weight of an object of mass m is the force of gravity that acts on it. From Newton’s second law, weight is given by W=mg.

If the only force acting on an object is its weight, then the object is in freefall.

Newton’s Third Law of Motion

Newton’s third law of motion states that when one body exerts a force on a second body, the first body experiences a force that is equal in magnitude and opposite in direction to the force that it exerts.

When an object rests on a surface, the surface applies a force on the object that opposes the weight of the object. This force acts perpendicular to the surface and is called the normal force.

The pulling force that acts along a stretched flexible connector, such as a rope or cable, is called tension. When a rope supports the weight of an object at rest, the tension in the rope is equal to the weight of the object.

Thrust is a force that pushes an object forward in response to the backward ejection of mass by the object. Rockets and airplanes are pushed forward by thrust.

Key Equations

Newton’s First Law of Motion: Inertia

• Newton’s first law of motionF_net= 0 or ΣF=0

Newton’s Second Law of Motion

• Newton’s second law of motionF_net=ma or ΣF=ma
• Newton’s second law of motion to solve accelerationa=F_net/m or a=ΣF/m
• Newton’s second law of motion to solve weightW=mg

Newton’s Third Law of Motion

• Normal force for a nonaccelerating horizontal surface N=mg
• Tension for an object at rest T=mg

Topic 2: Vector Motion (3h)

Prerequisite Skills:

• This section relies heavily on trigonometric ratios, solving for sides and angles, and Pythagoras’ theorem.

Figure 11 this—the Dragon Khan in Spain’s Universal Port Aventura Amusement Park. (credit: Boris23/Wikimedia Commons)

Everyday motion that we experience is, thankfully, rarely as tortuous as a rollercoaster ride like this—the Dragon Khan in Spain’s Universal Port Aventura Amusement Park. However, most motion is in curved, rather than straight-line, paths. Motion along a curved path is two- or three-dimensional motion and can be described in a similar fashion to one-dimensional motion.

Two Dimensional Motion: Walking in a City

Suppose you want to walk from one point to another in a city with uniform square blocks, as pictured in Figure 12.

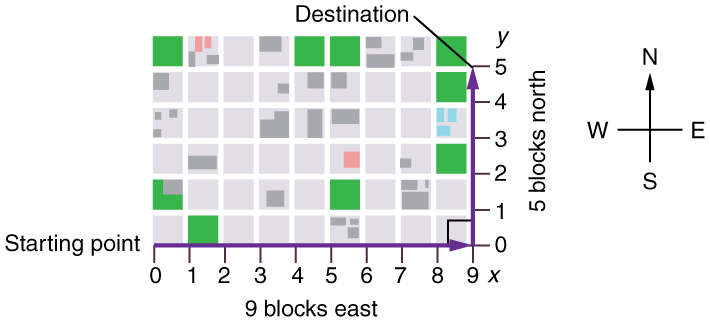
Figure 12 A pedestrian walks a two-dimensional path between two points in a city. In this scene, all blocks are square and are the same size.

The straight-line path that a helicopter might fly is blocked to you as a pedestrian, and so you are forced to take a two-dimensional path, such as the one shown. You walk 14 blocks in all, 9 east followed by 5 north. What is the straight-line distance?

An adage states that the shortest distance between two points is a straight line. The two legs of the trip and the straight-line path form a right triangle, and so the Pythagorean theorem, a² + b² = c², can be used to find the straight-line distance.

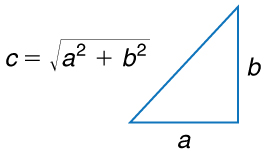
Figure 13 Pythagorean Theorem

The Pythagorean theorem relates the length of the legs of a right triangle, labeled a and b, with the hypotenuse, labeled c. The relationship is given by: a²+ b²= c². This can be rewritten, solving for c:

The hypotenuse of the triangle is the straight-line path, and so in this case its length in units of city blocks is

92 + 52 = 10.3,

or roughly 11 blocks (rounded up to the nearest whole block.) This is considerably shorter than the 14 blocks you walked.

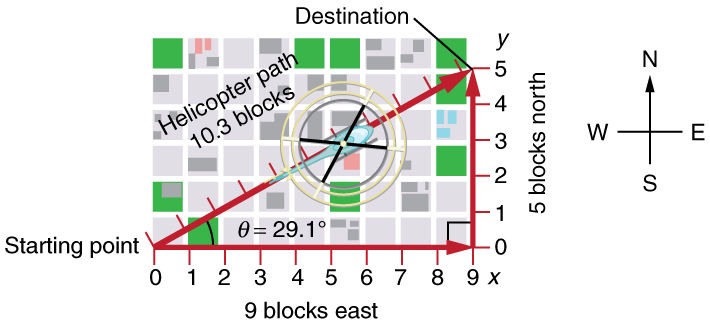
Figure 14 The straight-line path followed by a helicopter between the two points is shorter than the 14 blocks walked by the pedestrian. All blocks are square and the same size.

The fact that the straight-line distance (10.3 blocks) in Figure 14 is less than the total distance walked (14 blocks) is one example of a general characteristic of vectors. (Recall that vectors are quantities that have both magnitude and direction.)

We use arrows to represent vectors. The length of the arrow is proportional to the vector’s magnitude. The arrow’s length is indicated by hash marks in Figure 12 and Figure 14. The arrow points in the same direction as the vector. For two-dimensional motion, the path of an object can be represented with three vectors: one vector shows the straight-line path between the initial and final points of the motion, one vector shows the horizontal component of the motion, and one vector shows the vertical component of the motion. The horizontal and vertical components of the motion add together to give the straight-line path.

For example, observe the three vectors in figure 14. The first represents a 9-block displacement east. The second represents a 5-block displacement north. These vectors are added to give the third vector, with a 10.3-block total displacement. The third vector is the straight-line path between the two points.

Note that in this example, the vectors that we are adding are perpendicular to each other and thus form a right triangle. This means that we can use the Pythagorean theorem to calculate the magnitude of the total displacement. (Note that we cannot use the Pythagorean theorem to add vectors that are not perpendicular. We will develop techniques for adding vectors having any direction, not just those perpendicular to one another, in Vector Addition and Subtraction: Graphical Methods and Vector Addition and Subtraction: Analytical Methods.)

The Independence of Perpendicular Motions

The person taking the path shown in figure 14 walks east and then north (two perpendicular directions). How far he or she walks east is only affected by his or her motion eastward. Similarly, how far he or she walks north is only affected by his or her motion northward.

The horizontal and vertical components of two-dimensional motion are independent of each other. Any motion in the horizontal direction does not affect motion in the vertical direction, and vice versa.

This is true in a simple scenario like that of walking in one direction first, followed by another. In figure 12 and 14, the order you walk vertically and horizontally in does not matter. In fact, you could split horizontal and vertical in any combination. As long as the total horizontal blocks 9 and the number of vertical blocks is 5, you will end up at the same location.

The key to analyzing a vector in any direction is to resolve (break) it into motions along perpendicular directions. Resolving two-dimensional motion into perpendicular components is possible because the components are independent.

Vectors in Two Dimensions

Figure 15 Hawaiian Islands (credit: US Geological Survey)

A vector is a quantity that has magnitude and direction. Displacement, velocity, acceleration, and force, for example, are all vectors. In one-dimensional, or straight-line, motion, the direction of a vector can be given simply by a plus or minus sign. In two dimensions (2-d), however, we specify the direction of a vector relative to some reference frame (i.e., coordinate system), using an arrow having length proportional to the vector’s magnitude and pointing in the direction of the vector.

Figure 15 shows such a graphical representation of vector addition. The black segments form a path and when the lengths are added, represent the distance travelled. The net effect of traveling all those segments is represented by the dotted vector, which starts and the original point, and terminates at the end of the last segment. The dotted vector represents the displacement of the journey.

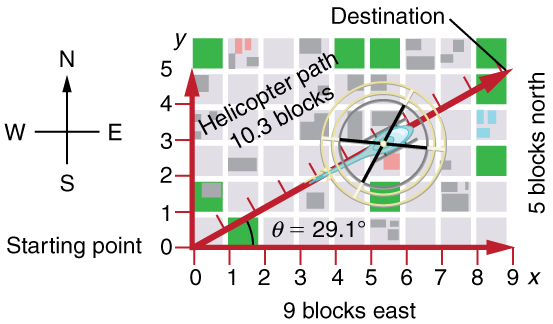
Figure 16 A person walks 9 blocks east and 5 blocks north. The displacement is 10.3 blocks at an angle 29.1˚ north of east.

Resolving a Vector into Components

We will need to take a single vector and find what other vectors added together produce it. In most cases, this involves determining the perpendicular components of a single vector, for example the x- and y-components, or the north-south and east-west components.

For example, we may know that the total displacement of a person walking in a city is 10.3 blocks in a direction 29.1˚ north of east and want to find out how many blocks east and north had to be walked. This method is called finding the components (or parts) of the displacement in the east and north directions.

If we are trying to add vectors going into different directions, we can resolve the vectors into x and y components. We can add all the x components together, and all of the y components together. We can then treat the combined x components as one large vector in the x direction, and the same for the y direction. Adding the total vector in the x direction with the total vector in the y direction will give the resultant vector, the same as if we had drawn the vectors with rulers and protractors.

Vector Addition and Subtraction: Analytical Methods

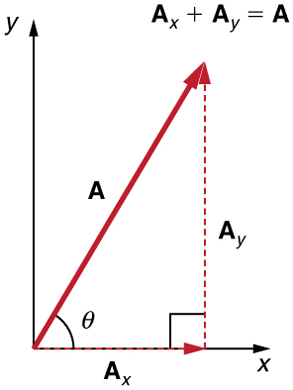
Figure 17 The vector A, with its tail at the origin of an x, y-coordinate system, is shown together with its x- and y-components, Ax and Ay. These vectors form a right triangle. The analytical relationships among these vectors are summarized below.

Analytical techniques and right triangles go hand-in-hand in physics because (among other things) motions along perpendicular directions are independent. We very often need to separate a vector into perpendicular components. For example, given a vector like A in figure 17, we may wish to find which two perpendicular vectors, A_x and A_y, add to produce it.

A_x and A_y are defined to be the components of A along the x- and y-axes. The three vectors A, A_x, and A_y form a right triangle:

Note that this relationship between vector components and the resultant vector holds only for vector quantities (which include both magnitude and direction). The relationship does not apply for the magnitudes alone. For example, if A_x = 3 m east, A_y = 4 m north, and A = 5 m north-east, then it is true that the vectors A_x + A_y = A. However, it is not true that the sum of the magnitudes of the vectors is also equal. That is,

Thus

If the vector A is known, then its magnitude A (its length) and its angle θ (its direction) are known. To find A_x and A_y, its x- and y-components, we use the following relationships for a right triangle:

And

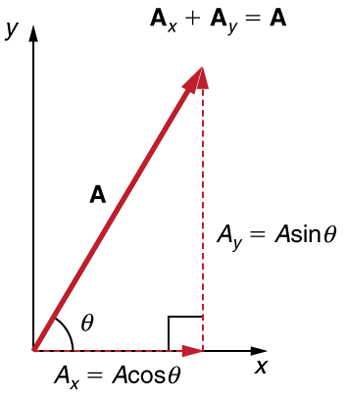
Figure 18 The magnitudes of the vector components A_x and A_y can be related to the resultant vector A and the angle ϴ with trigonometric identities. Here we see that and .
Remember from trigonometry:

And:

If we solve each equation for the A_x or A_y component, we get the following results (as labelled in figure 18.)

Suppose, for example, that A is the vector representing the total displacement of the person walking in a city.

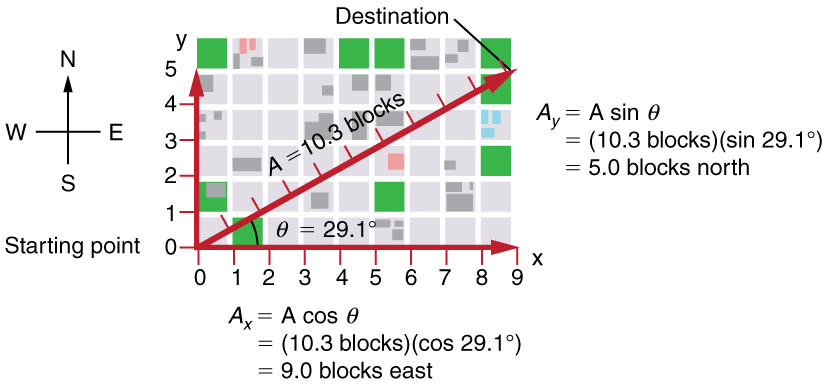
Figure 19 We can use the relationships Ax=Acosϴ and Ay=Asinϴ to determine the magnitude of the horizontal and vertical component vectors in this example.

Then A = 10.3 blocks and θ = 29.1˚ , so that

Calculating a Resultant Vector

If the perpendicular components A_x and A_y of a vector A are known, then A can also be found analytically. To find the magnitude A and direction θ of a vector from its perpendicular components A_x and A_y, relative to the x-axis, we use the following relationships:

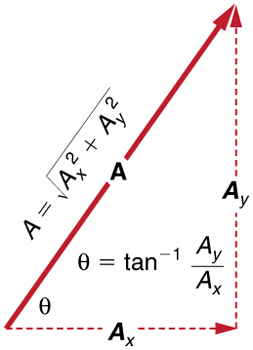
Figure 20 The magnitude and direction of the resultant vector can be determined once the horizontal and vertical components Ax and Ay have been determined.

Note that the equation

is just the Pythagorean theorem relating the legs of a right triangle to the length of the hypotenuse. For example, if A_x and A_y are 9 and 5 blocks, respectively, then

A = 92 + 52 = 10.3

blocks, again consistent with the example of the person walking in a city. Finally, the direction is

as before.

Application to Line Construction

You have learned how to calculate the angles and lengths involved with right angle triangles. You can use this information to solve tensions for guys, conductors, and the stress on poles which is called compression.

In the drawing below, if a line 15 m in the air has 800 lbs. of tension with an anchor 15 m from the pole, find the:

• Length of guy
• Tension on the guy
• Compression on the pole

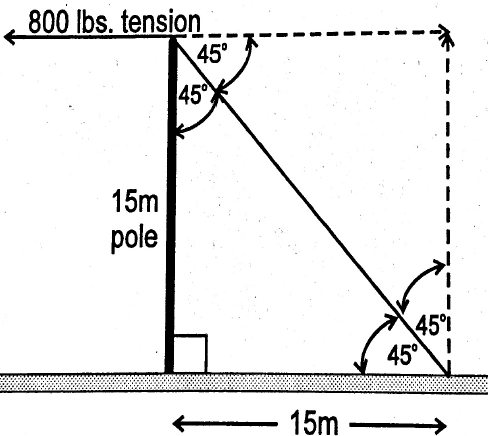
Solution

Length of guy:

Tension on guy:

Since two sides of the right angle triangle are of equal length, θ = 45 degrees.

Find the Hypotenuse:

Compression on the pole:

800 lbs., because a right angle triangle with 45 degrees is equal on both sides.

Example

From the above example, what happens when the anchor is moved in 5 m as shown in the diagram below? Find the length of guy, tension on guy, and compression on the pole.

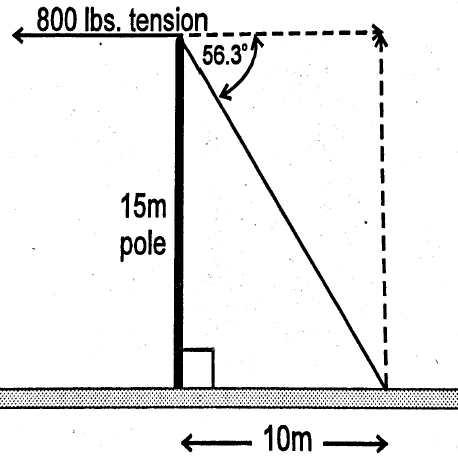
Solution

Length of guy:

Tension on guy:

Therefore,

Compression on the pole:

Example

Weight with Slings

To calculate the tension on a sling, you must realize it would take two slings to raise the load. The load is effectively split 50% for one sling and 50% for another.

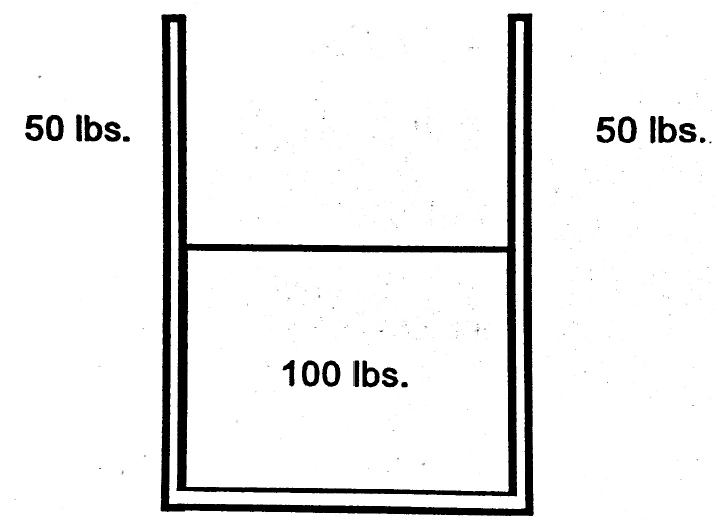
If you make a vector out of the sling angles, you can solve the tension easier.

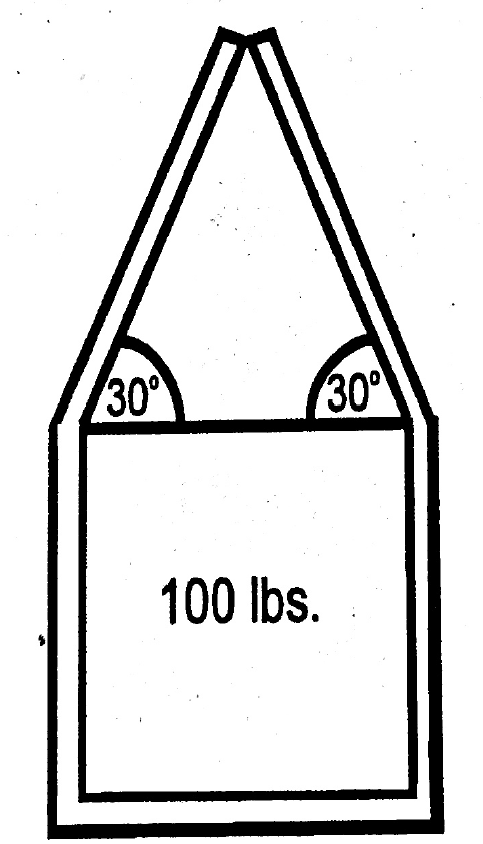
You know that the slings can be represented as two straight lines as shown below.

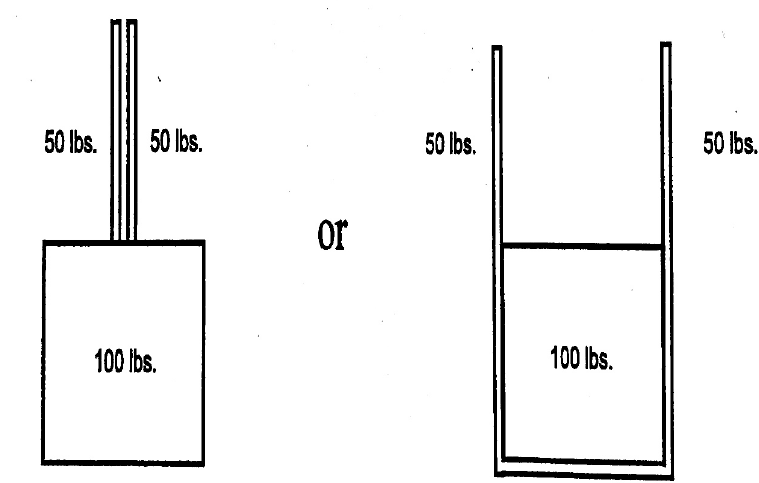
These can be solved using vectors in much the same manner as the pole and guy wire examples.

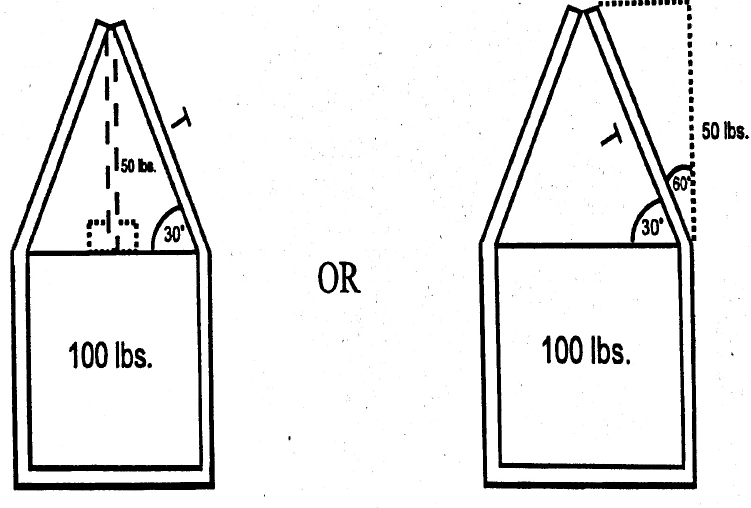
Tension = 100lbs/sling

Summary: Vector Addition and Subtraction: Analytical Methods

[h5p id=”9″]