IX. Música dodecafónica
Propiedades da serie
Mark Gotham and Brian Moseley
Puntos principais
- Algunhas series empréganse máis habitualmente que outras. Isto adoita deberse ás propiedades da serie.
- Este capítulo explica algunhas propiedades da serie que son bastante comúns:
- serie con todos os intervalos
- series derivadas
- Invariancia
- Combinatoriedade de hexacordos
- Conxuntos parcialmente ordenados
- A Antoloxía dodecafónica contén máis detalles sobre este tema.
Aínda que os compositores dodecafónicos consideren que as notas dunha serie son todas iguais, non parece que opinen o mesmo das diferentes formas da serie. De feito, as series que teñen certas propiedades atraeron moito máis a atención dos compositores. Este capítulo describe algúns tipos especiais de propiedades e formas de serie que cómpre coñecer. É habitual a énfase nas propiedades das partes máis pequenas que constitúen unha serie, os seus segmentos internos. Hai dúas formas de ver estas partes constituíntes: sobreposta e separada.
Segmentos sobrepostos e a serie con todos os intervalos
Considerarmos cada un dos segmentos “sobrepostos” dunha serie significa ver os segmentos comezando en cada altura, por quendas. Por exemplo, para as díades (dúas alturas, un intervalo), observamos as alturas 1 e 2, despois 2 e 3, continuando por 3 e 4, e así sucesivamente. Se consideramos dúas alturas de cada vez e avanzamos unha por unha, sempre haberá unha altura que se sobrepón. Este procedemento dános o contido interválico dunha serie e permítenos identificar o primeiro tipo de serie importante: a serie con todos os intervalos.
Aínda que todas as series dodecafónicas estándar inclúen as doce alturas diferentes, só algunhas conteñen os once intervalos posibles entre notas adxacentes (Exemplo 1). Hai 1.928 series diferentes que teñen esta propiedade e que se consideran serie con todos os intervalos, pero, como xa dixemos, unhas son máis usadas que outras. Unha propiedade que poden ter estas series é que haxa un trítono entre cada par de notas arredor do par central, isto é, entre as notas 1 e 12, 2 e 11, 3 e 10, 4 e 9, 5 e 8, e 6 e 7. No Exemplo 1, por exemplo, a serie comeza en La e remata en Re♯, etc.
Exemplo 1. An all-interval row from Luigi Nono, Il Canto Sospeso.
Este exemplo dunha serie con todos os intervalos é unha disposición lineal do que se denomina “acorde da avoa” (atribuído a Nicolas Slonimsky). Para producir esta sucesión de alturas, comezamos cun semitón ascendente (clase de intervalo 1), despois un ton descendente (clase de intervalo 10), e continuamos a alternar intervalos pares e impares, facendo que os impares sexan cada vez maiores e os pares, cada vez menores. Como consecuencia, a sucesión de alturas resultante pode interpretarse como a intercalación de dúas escalas cromáticas (como se observa no Exemplo 1), que é basicamente unha liña cromática con forma de cuña e podemos considerar que ten precedentes en obras tonais como as fugas de J. S. Bach (BWV 548) e Shostakovich (24 Preludios e fugas, Op. 87, n. 15).[1]
Segmentos separados e series “derivadas”
O método alternativo de segmentación é observar as partes separadas (non sobrepostas) da serie. Esta se cadra é a forma máis habitual de pensar nas formas da serie. Con esta limitación, unha serie dodecafónica pode ser dividida en seis díades, catro tricordos, tres tetracordos ou dous hexacordos. O feito de que haxa tantas opcións é unha propiedade do número 12 e un dos beneficios de ter un sistema baseado no 12.
Ao pasarmos dos segmentos sobrepostos aos separados, normalmente tamén centramos a atención máis no “só” que no “todos”. Especificamente, algúns compositores seriais tiveron interese en procuraren formas de serie que conteñen varias aparicións dun só conxunto de clases de altura.
O exemplo 2 é uha mostra clásica disto, e provén do Cuarteto de Corda Op. 28 de Anton Webern. As liñas que hai por baixo das notas indican os tres tetracordos separados que pertencen á mesma clase de conxunto: (0123), un tetracordo cromático. As ligaduras que hai sobre as notas mostran unha coherencia semellante nas díades separadas, que son sempre semitóns.
Exemplo 2. A row from Anton Webern’s String Quartet Op. 28, divided into discrete segments. Notice the limited number of set classes and intervals.
As series que teñen esta propiedade chámanse habitualmente series derivadas, o que significa que se pode considerar que a serie toda está composta por un conxunto de clases de altura (ou “deriva” del). Cómpre salientar que tamén hai un uso máis específico do termo, en que unha nova serie que ten esta propiedade deriva de forma directa dunha xa existente, cun dos conxuntos relevantes como subsegmento. Por exemplo, a serie de arriba puido derivar doutra serie que tamén tivese un subsegmento (0123).
Dunha perspectiva orientada á composición e á escoita, as series derivadas son moi suxestivas. Dado que o contido de clases de conxunto dunha serie non muda cando se transpón ou inverte, estas clases de conxunto circularán de forma constante pola peza, mesmo cando se empreguen outras formas da serie. Por tanto, unha serie derivada garante a recorrencia habitual de certas clases de conxunto, o que pode ser útil para favorecer un tipo concreto de unidade.
Invariancia (dos segmentos)
Invariancia significa preservación. Calquera atributo musical (como unha serie de intervalos, dinámicas, ritmos ou alturas) pode ser mantido dun contexto para o outro. Aínda que muden outras partes da música, este aspecto en cuestión non varía: de aí o termo “invariante”. Na teoría dodecafónica, o que máis nos importa é a invariancia interválica e a invariancia de segmentos de clases de alturas. O primeiro tipo, invariancia interválica, é moi común. Sempre que se transpón unha serie, o contido interválico ordenado dunha serie non varía. Do mesmo xeito, a retrogradación da inversión crea invariancia interválica retrógrada.
A invariancia dos segmentos é menos frecuente e merece un comentario á parte. Cando un segmento de clases de altura permanece igual se se transforma, dicimos que o segmento “permanece invariante” (Exemplo 3). O pentagrama superior reproduce a serie tal e como a vimos no Exemplo 2 (cos tetracordos separados), e o pentagrama inferior dispón a mesma serie transposta catro semitóns ascendentes (ou 8 descendentes, o que é o mesmo), é dicir, como P4. Repara en que estas dúas series (P0 e P4) conteñen os mesmos tetracordos, non só no relativo á clase de conxunto, senón tamén no referente ás alturas absolutas:
- As catro primeiras alturas de P0 (o primeiro compás do exmeplo) son as catro últimas alturas de P4. Isto aparece en azul claro.
- As catro alturas do medio de P0 (the second measure in the example) son as primeiras alturas de P4. Isto aparece en vermello.
- As catro últimas alturas de P0 (o derradeiro compás do exemplo) son as catro alturas do medio de P4. ISto aparece en azul escuro.
Estes tetracordos denomínanse segmentos invariantes. Os segmentos permanecen invariantes porque a relación que hai entre eles é a mesma que a que hai entre series: dado que os tetracordos só se relacionan por T8, ao transpor a serie toda para T8, os tetracordos “permanecen invariantes”. Dito doutra forma, cando o primeiro tetracordo se transpón a catro semitóns ascendentes, convértese no último tetracordo, entón cando a serie enteira se transpón a ese intervalo, acontece o mesmo.
Exemplo 3. Segmental invariance in Anton Webern’s String Quartet Op. 28.
Para determinarmos se un segmento de clases de alturas vai permanecer invariante:
- Encontramos unha clase de conxunto noutra parte da serie. Pode ser díade, tricordo, tetracordo, etc.
- Determinas a relación de transposición ou inversión entre eles.
- Cando se transpón ou inverte a serie con esa mesma relación, o segmento permanecerá invariante.
Hexacordos
Ao falar de series derivadas é habitual centrar a atención nos subsegmentos de tres ou catro notas, mais os dous hexacordos separados dunha serie (isto é, as dúas metades, alturas 1–6 e 7–12) atraeron polo menos a mesma atención dos teóricos e compositores ao longo dos anos, sobre todo no referente á combinatoriedade de hexacordos.
Combinatoriedade de hexacordos
Nunha serie dodecafónica estándar en que cada altura só aparece unha vez, o primeiro hexacordo (metade) de P0 complementa a segunda metade: entre as dúas, forman a colección cromática enteira. Dado que o primeiro hexacordo de R0 ten as mesmas alturas que o segundo hexacordo de P0 por definición, tamén podemos observar que os primeiros hexacordos de P0 e R0 son complementarios, pois forman a colección cromática completa. Isto demostra que tamén podemos encontrar hexacordos complementarios ao compararmos dúas formas de serie.
By definition, esta relación é establecida entre P0 e R0, así como outros pares de P–R e I–RI pairs (e.g., I4-RI4). Esta relación de “combinatoriedade” tórnase significativa cando se establece entre series relacionadas por outras transformacións, é dicir, entre pares P–P, P–I, ou P–RI. Na terminoloxía de Milton Babbitt, distinguimos entre dous graos nesta relación:
- Os pares semicombinatorios están relacionados por unha transformación destas: transposición (P–P), inversión (P–I), ou inversión da retrogradación (P–RI).
- Os pares completamente combinatorios (all-combinatorial) estçan relacionados por todas esas transformacións seriais. só hai seis series concretas que teñan esta propiedade, en que a relación se establece entre a serie e as súas transformacións. Un exemplo do repertorio é a serie da Sinfonía de Webern (tal e como exploraremos no seguinte no seguinte capítulo).
(014589): O “hexacordo máxico”
Just as the properties of some rows have attracted composers, so too have some hexachords. Imos presentar un hexacordo “famoso”: a clase de conxunto (014589), denominado “hexacordo máxico” (ou tamén “colección hexatónica“, “clase de conxunto hexatónica”, ou “hexacordo da Oda a Napoleón“). Este hexacordo ten as seguintes propiedades:
- Crea series completamente combinatorias de forma bastante fácil, por exemplo ao aplicar unha transposición de tres xeitos (+/-2 e 6 semitóns). Só a colección de tons enteiros (02468t) excede isto, pois a combinatoriedade establécese con calquera intervalo de número impar.
- Ten relación co modo con “modelo de distancia” 1:3 que se trata no capítulo das Coleccións.
- Contén moitas tríades internas, en concreto todas as alturas do ciclo hexatónica que se trata no capítulo dedicado á teoría neo-Riemanniana.
- Só ten un subconxunto de cinco notas posible, a clase de conxunto (01458).
- Só ten un superconxunto de sete notas posible: (0124589), que é o complemento do subconxunto de cinco notas, (01458).
- É utilizado en moitas obras, como o Concerto de Webern’s (como se describe no seguinte capítulo), a Oda a Napoleón de Schoenberg (de aí un dos seus nomes), e en obras de Maderna e Nono.
Conxuntos “parcialmente ordenados”
Cando pode ser que a música “serial” non sexa realmente serial? Por sorprendente que poida parecer, a resposta é “a miúdo”. Se, en sentido estrito, a música dodecafónica ten que estar baseada sistematicamente nunha sucesión fixa das doce alturas nunha versión simple (transposta e/ou invertida) dunha serie referencial, moita música que chamamos “serial” non funciona así realmente.
Un exemplo importante desta idea é a serie “parcialmente ordenada” (outro termo tomado das matemáticas), que nos fornece unha restrición máis flexible que se colocamos os doce sons nunha orde fixa. As series derivadas son unha boa introdución a esta situación. Como vimos, as series derivadas inclúen un contexto en que nos centramos nos segmentos constituíntes dunha serie (por exemplo, tetracordos) e a súa clase de conxunto. Só falta un pequeno paso para considerar que a “serie” poida estar definida maís polo contido destes segmentos do que por unha ordenación específica.
O exemplo 4 mostra a serie da Op. 28 de Webern unha vez máis (pentagrama superior), e crea unha nova serie dando a volta cada par de alturas (pentagrama inferior). O segundo caso ten os mesmos segmentos de díades e tetracordos que o primeiro, pero a orde interna deses segmentos mudou. Por definición, aínda temos unha serie coas doce alturas, só que é diferente.
Exemplo 4. Partially re-ordered row created from Anton Webern’s row in String Quartet, Op. 28.
A serie de Webern serve como exemplo, mais en realidade o concepto introduciuno máis tarde o compositor Milton Babbitt, e os tipos de reordenación poden tornarse máis complexos. Aínda que esta práctica se desvíe da definición “estrita” de 12 alturas nunha orde fixa, o que comparte é a reprodución constante da colección cromática completa (agregado). Alén disto, mesmo o serialismo “estrito” emprega aínda acordes (varias alturas que soan á vez), e para iso cómpre pensat máis no sentido da ordenación parcial que no estritamente serial. En resumo, é bastante común achar este tipo de pensamento, sexa dunha forma ou doutra.
Por último, é realmente significativo que as series estean relacionadas por unha ordenación parcial? Primeiro, lembra que hai centos de millóns de ordenacións diferentes das 12 alturas. Claro, hai menos cando fixas os hexacordos no seu sitio (e aínda menos para os subconxuntos menores), mais aínda continúan a ser moitos! Eis os números:
- Calquera ordenación das 12 alturas:
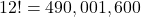
- Cos hexacordos fixos:
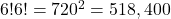
- Cos tetraordos fixos:
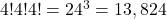
- Cos tricordos fixos:
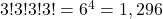
- Coas díades fixas:
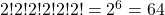
Xa só con isto, poderiamos considerar que non hai moita base para establecermos relacións significativas entre formas da serie, sobre todo cando o contido interválico muda con cada permutación de alturas. Como sempre acontece na análise, ao final o que nos interese é como se utiliza esta propiedade na práctica.
Outros tipos especiais de formas de serie
Este capítulo describiu só unhas poucas das moitas propiedades da serie que foron exploradas na historia. Rematamos cunha breve lista doutras, para que se vexa que hai moitas posibilidades.
Progresións de intervalos simétricos: Aínda que unha sucesión simétrica de alturas non é posible por razóns obvias (dado que non se repiten alturas durante a serie), si que é posible obter unha sucesión simétrica de intervalos, e as series que teñen esta propiedade teñen certa popularidade entre algúns compositores.
“Series cíclicas” (George Perle): Este termo refírese ás series en que se establecen pares de notas saltando unha, e todos os pares están separados polo mesmo intervalo, é dicir, que o intervalo entre as alturas 1 e 3 é o mesmo que entre 2 e 4, etc.
Series con máis ou menos de doce notas: Algúns compositores exploraron procesos seriais con series que teñen máis ou menos de doce notas. É evidente que isto causa algunhas propiedades diferentes (por exemplo, notas repetidas no caso das series con máis de doce notas), mais as prioridades e os procesos compositivos poden ser iguais. Como xa dixemos ao comezarmos a sección, o pensamento “serial” tnon está limitado ao pensamento dodecafónico. Algún exemplo sería:
| Ruth Crawford Seeger, Diaphonic Suite No. 1: | 7–9–8–11–0–5–1–7 (9 notas) |
| Ruth Crawford Seeger, Cuarteto de corda: | 2–4–5–3–6–9–8–7–1–0 (10 notas) |
| Elizabeth Lutyens, Requiescat In Memoriam Igor Stravinsky: | 6–8–4–2–11–0–3–1–5–7–10 (11 notas) |
| Elizabeth Lutyens, Chamber Concerto, Op. 8, n.º 1, mvmt. I: | 3–2–5–6–11–0–7–1–9–10–2–6–8–5–4 (15 notas) |
- Head to the Twelve-Tone Anthology and pick any row listed in the sections on derived rows (e.g., “6x Same Dyad (interval)” or “4x Same Trichord”).
- Write out the full row in musical notation.
- Put slur lines over each repeated segment (e.g., 4 x 3 notes in the “4x Same Trichord”).
- Separately (e.g., below), write out those subsegments as chords.
- That the wedge is the subject of a fugue in both these cases, and therefore a central focus, recurring frequently throughout, perhaps strengthens the connection. ↵
A twelve-tone row that contains all eleven ordered pitch-class intervals.
A 12-tone tonerow formed of the same pitch class set several time such as 3 tetrachords or 4 trichords.
The ordered elements in a serial composition, also referred to as a series. These elements are often pitches, but could be other things such as durations or dynamics.
A particular version of a row in serial music; that is, prime, transposed, inverted, or retrograded.
Non-overlapping; separate.
A portion of a larger grouping. In serial analysis, segments of a row can be any number of elements (for example, in a twelve-tone row, it's common to look at three- or four-note segments).
A group of pitch-class sets related by transposition or inversion. Set classes are named by their prime forms; for example, (012) is a set class.
In serial music, invariance refers to keeping a property of a row the same through different transformations. For example, when a retrograde version of a row contains the same ordered pitch classes as a prime version of the row, we would call it "retrograde invariant" to mean that the order of pitch classes doesn't change when the row is reversed and transposed
A six-note collection. In serial music, "hexachord" is typically used to refer to either the first or last six notes of a twelve-tone row.
A property of a row in which combining one hexachord from a version of a row with a hexachord from another version of a row creates the chromatic collection.
The set that, together with an original set, will make the complete twelve-tone collection. Complements are literal when referring to pitch class sets and abstract when referring to set classes.
A six-note collection that alternates between half steps and minor thirds, such as C–C♯–E–F–G♯–A.
A pitch collection composed entirely of whole steps. There are six whole steps in a whole tone collection, and there are only two possible whole tone scales: C–D–E–F♯–G♯–A♯, or C♯–D♯–F–G–A–B.
The complete chromatic collection (i.e., all twelve pitch classes).
