V. Chromaticism
Harmonic Elision
Brian Jarvis
Key Takeaways
- Harmonic elision is the suppression of an expected chord (distinct from chord substitution).
- Leading-tone elision:
- The expected triad is replaced by the dominant seventh chord with the same root or by a functionally equivalent diminished seventh chord.
- The leading tone (or applied leading tone) is altered to become te
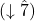 instead of resolving up by minor second.
instead of resolving up by minor second. - The same bass note is maintained unless the bass had the leading tone (or applied leading tone).
- Raised-root elision:
- The root of the expected chord is raised to become a leading tone (or applied leading tone).
- The new chord can typically be V, V7, or viio7.
- The bass should be as close to the expected bass note as possible.
Harmonic elision occurs when a harmonic progression seems to suppress or remove an expected chord for one that is similar but functionally distinct from the chord it replaced. It often feels like the combination of two simultaneous harmonic events. This is different from chord substitution, where the replacement of an expected chord just seems like a single unexpected event. However, some use the term “chord substitution” in a broader sense that would also include harmonic elision as described here. This chapter covers two types of elision: leading-tone elision and raised-root elision.
Context
Leading-tone elision with a dominant seventh chord
A leading-tone elision occurs when a chord has a leading tone (or an applied leading tone) that doesn’t resolve as expected (up by minor second) and instead becomes the lowered version of itself (e.g., B becomes B♭ or C♯ becomes C♮). This can happen when a dominant-functioning chord resolves not to the expected triad but to a dominant seventh with the same root as the expected triad, as in Example 1. Note that the suppressed chord can be clearly identified given what we expect to happen in this harmonic context.
Example 1. A harmonic elision where the expected chord is suppressed and replaced with a dominant seventh with the same root.
Leading-tone elision with a fully diminished seventh chord
Leading-tone elision can also occur when an expected triad is replaced by a fully diminished seventh chord that is functionally equivalent to the dominant seventh chord that could have replaced it (if there is one) and has the same bass note. Example 2 shows each inversion of a V7 chord and the functionally equivalent viio7 chord that can be used instead.
Example 2. Functionally equivalent V7 and viio7 chords.
Example 3 contains an example of this type of leading-tone elision. Notice that Examples 1 and 3 are nearly identical except that Example 3 is using the functionally equivalent fully diminished seventh chord instead (viio7 instead of ![]()
Example 3. A harmonic elision where the expected chord is suppressed and replaced with a fully diminished seventh chord that has an equivalent function to the dominant seventh in Example 1.
Voice leading with leading-tone elision
When dealing with elision, the voice leading doesn’t change much; the only difference is that the leading tone becomes the lowered version of itself instead of resolving up by minor second to the root of the next chord as it normally would. See the voice-leading comparison in Example 4.
Example 4. Voice-leading comparison between a regular resolution and an elided one.
When the leading tone is in the bass
It is important to remember that if the leading tone before a leading-tone elision is in the bass, this means the bass will change, putting the upcoming chord in a different inversion. This is expected to happen with V6, V65, and viio7 (and any applied chords with the same Roman numerals) because they all have the leading tone in the bass. Common progressions for this occurrence are ![]() and
and ![]() , as in Example 5 below. In other situations, the bass note will stay the same.
, as in Example 5 below. In other situations, the bass note will stay the same.
Example 5. Change of expected bass when the leading tone is in the bass and a leading-tone elision occurs.
Raised-Root Elision
Raised-root elision occurs when the root of the expected chord arrives in its raised version (e.g., B♭ becomes B♮ or C becomes C♯) to become the leading tone in an applied chord. For example, a raised-root elision would occur if an expected chord with C as the root was suppressed and a chord with C♯ as a leading tone appeared instead. This could be any of the chords that use C♯ as a leading tone: A, A7, C♯o, C♯o7 and C♯∅7 (though the half-diminished option is not very common). The overall harmonic result is that the progression is pushed higher up the scale. In Example 6, the expected progression (based upon norms in this style) would be ![]() . Instead, the final I chord is elided with a raised-root elision, because
. Instead, the final I chord is elided with a raised-root elision, because ![]() (A7/C♯) takes its place. That chord then resolves to ii, so while the expected progression was heading toward I, the end result of the raised-root elision is that the progression resolves to ii, one step higher in the scale.
(A7/C♯) takes its place. That chord then resolves to ii, so while the expected progression was heading toward I, the end result of the raised-root elision is that the progression resolves to ii, one step higher in the scale.
Example 6. Raised-root elision.
The 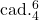 version
version
Progressions with ![]() can contain raised-root elision that is a little different because the expected root does appear with the arrival of the
can contain raised-root elision that is a little different because the expected root does appear with the arrival of the ![]() but transforms into its raised version when the
but transforms into its raised version when the ![]() resolves to the
resolves to the ![]() . Example 7 illustrates this situation.
. Example 7 illustrates this situation.
Example 7. Raised root elision involving ![]() .
.
Finding Harmonic Elision
Harmonic elision is fairly easy to spot in Roman numeral analysis because you will notice incongruities in the sequence of symbols. For example, if you see the Roman numeral ![]() , you would expect I to follow, but with a leading-tone elision, you could see
, you would expect I to follow, but with a leading-tone elision, you could see ![]() followed directly by
followed directly by ![]() , which should alert you to the fact that something unexpected has occurred. After looking at the progression, you can conclude that harmonic elision has taken place—you analyzed the chord correctly, but the chord you expected has been elided. The same is true for raised-root elision: if you saw
, which should alert you to the fact that something unexpected has occurred. After looking at the progression, you can conclude that harmonic elision has taken place—you analyzed the chord correctly, but the chord you expected has been elided. The same is true for raised-root elision: if you saw ![]() followed directly by
followed directly by ![]() instead of the expected V, you could investigate further and conclude that the V chord has been elided, with its root raised to become the leading tone of vi.
instead of the expected V, you could investigate further and conclude that the V chord has been elided, with its root raised to become the leading tone of vi.
Notation: When an elision occurs, it’s good practice to write the expected Roman numeral in your analysis but then cross it out and place the symbol for the chord that actually occurred. Example 8 below shows an example of this style of notation.
Musical Example
The first phrase of Richard Strauss’s song “Zueignung” (Example 8) includes three harmonic elisions. The first occurs on beat 4 of measure 6. It is expected that the G major chord on beat 3 will be followed by a C major chord, but the C major chord has been suppressed, and in its place, a chord with a C♯ is used instead. This is a raised-root elision because the expected root was C and a chord with C♯ occurred instead, with the C♯ functioning as an applied leading tone.
The second harmonic elision occurs in m. 8, where a quasi ![]() (without the expected 4–3 part of the chord, but otherwise quite similar) never resolves to its
(without the expected 4–3 part of the chord, but otherwise quite similar) never resolves to its ![]() version. Instead, the expected root, G, is suppressed and a G♯ appears in its place (as an applied leading tone to vi), making this another instance of a raised-root elision.
version. Instead, the expected root, G, is suppressed and a G♯ appears in its place (as an applied leading tone to vi), making this another instance of a raised-root elision.
Measure 9 repeats the quasi ![]() chord again. This time, it resolves to a chord with C as the root, but it still isn’t the root-position tonic triad we expect. Instead, we find a leading-tone elision: the dominant’s leading tone resolves down, making the C chord a dominant seventh (V7/IV).
chord again. This time, it resolves to a chord with C as the root, but it still isn’t the root-position tonic triad we expect. Instead, we find a leading-tone elision: the dominant’s leading tone resolves down, making the C chord a dominant seventh (V7/IV).
Example 8. Richard Strauss, “Zueignung“, Op. 10, no. 1, mm. 1–10 – Multiple harmonic elisions in a single phrase.
- Harmonic Elision (.pdf, .docx.) Asks students to spell chords, realize figured bass, write 4-part voice leading with Roman numerals, and analyze a musical excerpt.
The suppression of an expected chord. Two kinds of elision are a leading-tone elision, in which the expected triad is replaced by the dominant seventh chord with the same root or by a functionally equivalent diminished seventh chord, and raised-root elision, in which the root of the expected chord is raised to become a leading tone (or applied leading tone).
A 7̂ that is one half step below 1̂. The leading tone is diatonic in major keys, but requires an accidental in minor keys.
The lowest note of a triad or seventh chord when the chord is stacked in thirds.
