IV. Diatonic Harmony, Tonicization, and Modulation
Prolongation at Phrase Beginnings using the Leading-Tone Chord
John Peterson
Key Takeaways
- Instead of using an inverted
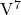 chord to prolong tonic, composers sometimes use
chord to prolong tonic, composers sometimes use 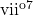 or its inversions.
or its inversions. - Each inversion of
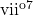 can be used in the same way as a particular inversion of
can be used in the same way as a particular inversion of 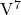 . The pairings of
. The pairings of 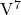 and
and 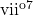 are based on the bass note each chord harmonizes.
are based on the bass note each chord harmonizes.
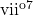 can be used anywhere that
can be used anywhere that 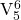 or
or 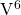 can be used.
can be used.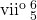 or
or 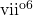 can be used in place of
can be used in place of 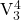 .
.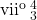 can be used in place of
can be used in place of 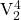 .
.
Overview
Earlier, we saw how the tonic can be prolonged using essentially four kinds of progressions, which we categorized according to their basslines (see the summary section of that chapter for a reminder). In this chapter, we consider an alternative way to harmonize those same tonic-prolongation bass lines using a harmony that can substitute for V7: the leading-tone chord. Example 1 shows a passage from Mozart’s “Agnus Dei” that uses viio7 and its inversions to prolong tonic. Below the actual version, a recomposition shows that the bass line from the actual version can also be harmonized with V7 and its inversions. As you listen, notice the differences in color between the two versions. You may hear that the actual version is full of a wonderful tension that is less present in the recomposed version.
Example 1. Using viio7 vs. V7 in Mozart, “Agnus Dei” from Requiem (0:06–0:20).
Before we address how this substitution works, here are three points we need to emphasize:
- The leading-tone chord as a triad is always used in first inversion viio6. This is because any other inversion creates a dissonance with the bass that composers tend to avoid.
- In minor, we need to remember to use ti
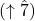 , not te
, not te 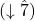 , to build the leading-tone chord. In other words, remember to raise the leading tone.
, to build the leading-tone chord. In other words, remember to raise the leading tone. - In major, the leading-tone seventh chord’s quality is half diminished if we don’t alter it (e.g. in C major: B-D-F-A). Composers tend to prefer the sound of a fully diminished 7th chord, though, so we nearly always find that in major keys, composers lower the chordal seventh to make the chord fully diminished (e.g., in C major: B-D-F-A♭) (Example 2). You can use both, but viio7 is much more common than vii∅7, and we’ll see why below.
Example 2. Comparing qualities of leading-tone seventh chords.
Substituting the leading-tone chord in place of V(7)
Almost all inversions of ![]() (plus
(plus ![]() can substitute for an inversion of
can substitute for an inversion of ![]() (and
(and ![]() according to which note is in the bass (Example 3). What this means is that, for example,
according to which note is in the bass (Example 3). What this means is that, for example, ![]() can be used anywhere that
can be used anywhere that ![]() or
or ![]() can be used. Similarly,
can be used. Similarly, ![]() or
or ![]() can be used in place of
can be used in place of ![]() , and
, and ![]() can be used in place of
can be used in place of ![]() .
.
[table “43” not found /]
Example 3. Substituting viio7 for V7 according to which note is in the bass.
Luckily, there isn’t too much else to learn with respect to part writing. Continue to follow typical part-writing procedures and to resolve active notes in the upper voices according to their tendencies. Example 4 reviews these tendencies and adds the one new note we haven’t seen yet in a dominant-function chord: le/la ![]() /
/![]() . Example 5 shows tonic prolongations involving viio7 and its inversions, and it compares each to a corresponding prolongation involving
. Example 5 shows tonic prolongations involving viio7 and its inversions, and it compares each to a corresponding prolongation involving ![]() and its inversions.
and its inversions.
[table “44” not found /]
Example 4. Tendencies of active notes in dominant-function chords.
Example 5. Writing with ![]() and
and ![]() and its inversions.
and its inversions.
viio4/2
You might have noticed that ![]() doesn’t correspond to an inversion of
doesn’t correspond to an inversion of ![]() . That’s because it’s built on le
. That’s because it’s built on le ![]() , which isn’t in
, which isn’t in ![]() .
. ![]() is a very rare harmony because the expected resolution from le down to sol
is a very rare harmony because the expected resolution from le down to sol ![]() (see Example 4) occurs in the bass. So far, we’ve seen that sol
(see Example 4) occurs in the bass. So far, we’ve seen that sol ![]() in the bass typically supports V or
in the bass typically supports V or ![]() , and that’s also the case here:
, and that’s also the case here: ![]() goes to
goes to ![]() (Example 6). Again, though,
(Example 6). Again, though, ![]() is not a very common chord.
is not a very common chord.
Example 6. Using ![]() .
.
Using the leading-tone chord as a half-diminished seventh chord
vii∅7 presents voice-leading challenges that are not present with viio7 because it contains a perfect fifth between re ![]() and la
and la ![]() . This is perhaps another reason that composers favor viio7 over vii∅7: with ∅7, we need to watch out for parallel fifths, as in Example 7. An easy way to avoid them is to always make sure that re
. This is perhaps another reason that composers favor viio7 over vii∅7: with ∅7, we need to watch out for parallel fifths, as in Example 7. An easy way to avoid them is to always make sure that re ![]() is above la
is above la ![]() when you use vii∅7 or its inversions. The one time where this advice is impossible is with
when you use vii∅7 or its inversions. The one time where this advice is impossible is with ![]() , where re
, where re ![]() is in the bass. Although it’s possible to avoid parallels with
is in the bass. Although it’s possible to avoid parallels with ![]() , we’d recommend just using
, we’d recommend just using ![]() instead.
instead.
Example 7. Using ![]() and its inversions.
and its inversions.
- Prolongation at Phrase Beginnings using the Leading-tone Chord (.pdf, .docx). Asks students to write from Roman numerals, complete analysis, and realize figured bass.
The triad or seventh chord built on ti (7̂).
1. Write the entire bass
2. Write the entire soprano to make a smooth melody that interacts well with the bass. Choose active notes for the soprano above dominant-function chords, and remember you do not always need to write left to right.
3. Write the inner voices by asking, "What notes do I already have? What notes do I still need? Considering spacing and resolution, what note placement would give me the smoothest motion?"
