VIII. Técnicas dos séculos XX e XXI
Os intervalos na notación con números enteiros
Brian Moseley and Megan Lavengood
Puntos principais
- Ao analizarmos música atonal, podemos entender mellor os intervalos como número de semitóns, en vez de usar os nomes dos intervalos na tonalidade.
- Hai catro tipos de intervalo: intervalos de alturas ordenados, intervalos de alturas non ordenados, intervalos de clases de altura ordenados e clases de intervalo (intervalos de clases de altura non ordenados).
- Os intervalos de altura ordenados son os máis específicos: miden alturas específicas (en oitavas específicas) e representan a direccionalidade do intervalo.
- As clases de intervalo son o tipo máis abstracto de intervalo: representan a menor ditancia posible entre dúas clases de altura.
Na música tonal, como os intervalos dependen das alturas que os crean, a consonancia ou disonancia dos intervalos vén determinada pola propia tonalidade. Imaxina un intervalo creado entre Sol e Si♭, unha terceira menor. No contexto de Sol menor, é un intervalo consoante. Se o reescribimos como Sol e La♯, por exemplo no contexto de Si menor, crea unha segunda aumentada disonante. Dunha perspectiva tonal, por tanto, os dous intervalos son diferentes aínda que soen igual sen contexto (Exemplo 1).
Exemplo 1. Aínda que Si♭ e La♯ son a mesma tecla nun teclado, os intervalos de terceira menor e segunda aumentada son diferentes na teoría tonal.
Compárao coa música atonal. Dado que a música atonal non ten tonalidade, a distinción entre Si♭ e La♯ xa non importa. Neste contexto, os intervalos Sol–Si♭ e Sol–La♯ son o mesmo. Por esta razón, non usaremos os nomes tonais dos intervalos, como “terceira menor”. Así, mediremos os intervalos polo número de semitóns que hai entre alturas ou clases de altura.
Podemos describir os intervalos segundo dous tipos de información: alturas vs. clases de altura, e intervalos ordenados vs. non ordenados. Combinándoos, obtemos catro tipos de intervalos, que se resumen no Exemplo 2. Cada tipo de intervalo está explicado máis adiante.
| Intervalos de alturas | Intervalos de clases de alturas | |
|---|---|---|
| Intervalos ordenados | intervalos de alturas ordenados | intervalos de clases de altura ordenados |
| Intervalos non ordenados | intervalos de alturas non ordenados | intervalos de clases de altura non ordenados / clases de intervalo (IC) |
Exemplo 2. Catro tipos de intervalo na teoría atonal.
Intervalos de alturas (ordenados e non ordenados)

Os intervalos de alturas (pitch intervals) son a distancia que hai entre alturas medida en semitóns, o que significa que temos en conta a oitava. Así, o intervalo Dó4–Mi4 é 4: hai catro semitóns entre estas notas. Porén, se ese Mi está na oitava superior (Dó4–Mi5), o intervalo é 16: catro semitóns entre C e E, máis unha oitava (doce semitóns) entre o Mi grave e o agudo.
Nos intervalos de alturas, temos variantes ordenadas e non ordenadas. Para crear un intervalo de alturas ordenado, só hai que engadir un signo de suma ou resta para indicar se o intervalo é ascendente ou descendente. Os intervalos de alturas non ordenados, polo contrario, non indican en que dirección se moven as alturas, e por tanto son máis adecuados para os intervalos harmónicos. As diferenzas entre os intervalos de alturas ordenados e os non ordenados está resumida no Exemplo 3 [fai clic para ampliares a imaxe].
Intervalos de clases de altura ordenados
Os intervalos de clases de altura (pitch-class intervals) son a distancia que hai entre clases de altura medidas en semitóns no espazo das clases de altura, é dicir, nun reloxo. Se retomamos o noso intervalo Dó4–Mi5, agora centramos a atención só nas clases de altura Dó e Mi, sen referencia a unha oitava específica.
Os intervalos de clases de altura ordenados miden a distancia entre clases de altura, sempre de xeito ascendente. É máis fácil visualizarmos isto se pensamos nas doce notas no reloxo e despois medimos o intervalo percorrendo o círculo no sentido horario. Así, de C a E = 4, mais E a C = 8 (Exemplo 4).
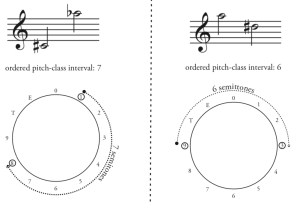
Clases de intervalo (IC)
Os intervalos de clases de altura non ordenados adoitan chamarse clases de intervalo (interval classes). Unha clase de intervalo é a menor distancia posible que hai entre dúas clases de altura. No reloxo, isto significa que nos movemos tanto no sentido horario como no antihorario, o que sexa máis curto. O concepto de clase de intervalo é útil porque relaciona os intervalos, as súas inversións e calquera versión composta deles. Poderíamos establecer unha conexión entre este concepto e a relación entre altura e clase de altura: unha clase de altura é unha altura, a(s) súa(s) alternativa(s) enharmónica(s) e as diferentes oitavas de todas esas posibilidades.
Isto significa que só hai seis clases de intervalo: 1, 2, 3, 4, 5, e 6. Se alcanzas o intervalo de clases de altura 7, xa é máis curto o sentido antihorario e o 7 tórnase 5. Por esta mesma razón, o 8 tórnase 4, o 9 tórnase 3, e así por diante. Tanto Dó–Mi como Mi–Dó son a clase de intervalo 4 (Exemplo 5).
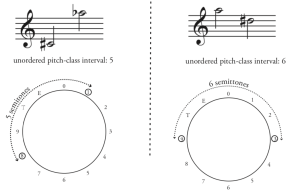
Resumo
Se usamos as diferentes combinacións de intervalo de alturas, intervalo de clases de altura, intervalo ordenado e intervalo non ordenado, obtemos catro concepcións diferentes do intervalo. Para poderes interiorizar cada unha delas e comezar a comprender as súas utilidades analíticas, podes pensar neles nunha escala que vai do máis concreto (o intervalo de alturas ordenado) ao máis abstracto (o intervalo de clases de altura non ordenado). Podes encontrar esta organización, en relación con outros conceptos, na Ficha de referencia rápida para a teoría dos conxuntos (en inglés).
Na música tonal, é útil distinguirmos entre unha décimo terceira e unha sexta nalgunhas situacións, mais non noutras. Do mesmo xeito, cando analices música atonal, verás que os diferentes tipos de intervalos son útiles para describirmos diferentes tipos de fenómenos.
- Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. Upper Saddle River, NJ: Prentice Hall.
- Blank clock faces (integer notation)
- Blank clock faces (letter names)
- Set Theory Quick Reference Sheet: summarizes the definitions of pitch vs. pitch class, intervals vs. interval classes, and sets vs. set classes.
- Intervals (.pdf, .docx). Asks students to identify interval types (integer notation) within pieces of music. Worksheet playlist
Media Attributions
- Ordered vs unordered pitch interval
- Ordered pitch class intervals
- Pitch classes
An adjective describing music that lacks any sense of tonal center.
One-twelfth of an octave; generally considered to be the smallest interval in Western musical notation.
The distance between two pitches measured in semitones, with a plus or minus symbol to indicate ascending or descending, respectively. For example: C₄ to E₅ would be an ordered pitch interval of +16.
The distance between two pitches, measured in semitones. For example, C₄ to E₅ would be an unordered pitch interval of 16.
The distance between pitch classes from lowest to highest. In other words, pitch class intervals are measured on the clock face, always going clockwise.
Unordered pitch-class intervals; that is, the smallest possible distance in semitones between two pitch classes. Thus, mi2 and ma7 are both IC 1; ma2, mi7, +6 are IC 2; mi3, ma6, +2 are IC 3, etc. The largest interval class is six semitones, because if order is disregarded, the tritone is the largest possible interval.
An adjective used to describe music that adheres to the Western system of functional harmony.
A discrete tone with an individual frequency.
A group of pitches that are octave equivalent and enharmonically equivalent.
