VIII. Técnicas dos séculos XX e XXI
Altura e clase de altura
Megan Lavengood
Puntos principais
- A teoría dos conxuntos baséase moito na distinción entre altura e clase de altura.
- As clases de altura represéntanse mellor coa notación de números enteiros, na cal Dó=0.
Altura
As alturas son sons específicos con frecuencias diferenciadas.
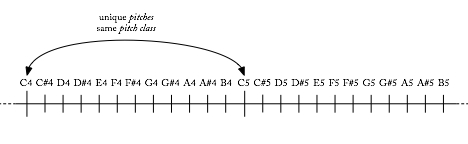
O concepto de altura, por tanto, non implica equivalencia de oitava. Dó4 é unha altura, e non é a mesma altura que Dó3.
Clase de altura
Na teoría dos conxuntos, a palabra “clase” significa “grupo”. Deste xeito, unha clase de altura (pitch class) é un grupo de alturas, todas as alturas que están relacionadas pola equivalencia das oitavas e a equivalencia enharmónica. E probable que xa coñezas eses conceptos de antes, aínda que non usases eses nomes.
O noso sistema para dar nome ás notas implica a equivalencia das oitavas: equivalencia entre alturas que se chaman igual pero que están a unha ou máis oitavas de distancia. Dó4 é a mesma nota que Dó3, que é a mesma que Dó9, e así sucesivamente, porque todos son Dós (Exemplo 1).
Cando alguén di “hai doce notas”, está a asumir que hai equivalencia enharmónica. Dúas notas son equivalentes enharmonicamente se son tocadas na mesma tecla do piano, a pesar de que a súa escrita sexa diferente. A equivalencia enharmónica é a razón pola cal La♭e Sol♯ son “o mesmo”. Aínda que a música tonal case sempre diferencia entre alturas enharmónicas (La♭ como 
leva a Sol, mais Sol♯ como 
leva a La) a música postonal adoita ser diferente.[1] Dado que moitos compositores xa non optan por cinguirse ás limitacións dun centro tonal, a relación entre os graos da escala e a escrita das notas non é importante.
En resumo, as clases de altura (pitch classes) son grupos de alturas que están relacionadas pola equivalencia enharmónica ou de oitava. La♭4, La♭3, Sol♯2, etc. son todas membros da mesma clase de altura.
Exemplo 1. Pitch versus pitch class.
Notación con números enteiros
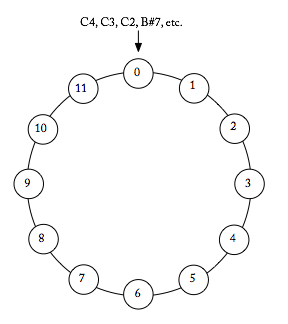
Se as notas son equivalentes enharmonicamente, entón o sistema de sete nomes para as notas non funciona tan ben para describir as doce clases de altura. Na teoría dos conxuntos, emprégase máis a notación con números enteiros, que asigna un número entre 0 e 11 a cada clase de altura (Exemplo 2). Todos os Dós, e calquera nota que sexa equivalente enharmonicamente a Dó (Si♯, por exemplo), son a clase de altura 0. Todos os Dó♯s, e calquera nota que sexa equivalente enharmonicamente a C♯ (Re♭, por exemplo) son a clase de altura 1, e así por diante. Podemos resumilo deste xeito, cos nomes máis habituais das notas:
- Dó (Si♯, etc.)
- Dó♯, Re♭
- Re (Dó𝄪, etc.)
- Re♯, Mi♭
- Mi (Fa♭, etc.)
- Fa (Mi♯, etc.)
- Fa♯, Sol♭
- Sol (Fa𝄪, etc.)
- Sol♯, La♭
- La (Sol𝄪, etc.)
- La♯, Si♭
- Si (Dó♭, etc.)
- Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. Upper Saddle River, NJ: Prentice Hall.
- Blank clock faces (integer notation)
- Blank clock faces (letter names)
- Set Theory Quick Reference Sheet: summarizes the definitions of pitch vs. pitch class, intervals vs. interval classes, and sets vs. set classes.
- Pitch and pitch class (.pdf, .mscz). Asks students to translate between pitch class integers, note names, and staff notation.
Media Attributions
- Pitch Space
- Pitch-class-Space
- Post-tonal music is extremely various. Composers have individual compositional styles, aesthetic goals, and unique conceptions of pitch. All this is to say that you must approach a composition with flexibility. For example: because it is quasi-tonal, Debussy’s music often benefits from a view that does not assume enharmonic equivalence. But sometimes it does. You must rely on your musical intuitions when analyzing this music, and you should also be willing to approach pitch in these compositions from multiple perspectives until you find one that seems most appropriate. ↵
A methodology for analyzing pitch in atonal music. Pitch classes are given an integer name (0–11, where C is 0, C♯ is 1, etc.). Groups of pitches are considered together as "sets." Sets may be related by inversion or transposition.
A discrete tone with an individual frequency.
A group of pitches that are octave equivalent and enharmonically equivalent.
A system of naming pitch classes that treats C as 0, C♯ as 1, D as 2, etc.
A relationship between pitches that share a letter name but are separated by one or more octaves.
A relationship between notes, intervals, or chords that sound the same but are spelled differently.
