Learning Goals

By the end of this reading you should be able to:
  • Relate population genetics to the processes of evolution
  • Explain how the Hardy-Weinberg principle is used in the biological sciences.
  • Given an allele frequency calculate the frequency of different genotypes in a population. 
  • Use the Hardy-Weinberg principle to determine if a  population is evolving. 
While we currently have a complex understanding of the mechanisms of inheritance, or genetics, when Charles Darwin and Alfred Russel Wallace were developing their idea of natural selection this knowledge was unavailable. Not understanding how traits were inherited created a stumbling block to understanding many aspects of evolution. In fact, the predominant (and incorrect) genetic theory of the time, blending inheritance, made it difficult to understand how natural selection might operate. Darwin and Wallace were unaware of the genetics work by Austrian monk Gregor Mendel, which was published in 1866, not long after the publication of Darwin’s book, On the Origin of Species. Mendel’s work was rediscovered in the early twentieth century at which time geneticists were rapidly coming to an understanding of the basics of inheritance. Initially, the newly discovered particulate nature of genes made it difficult for biologists to understand how gradual evolution could occur. But over the next few decades, genetics and evolution were integrated in what became known as the modern synthesis—the coherent understanding of the relationship between natural selection and genetics that took shape by the 1940s and is generally accepted today. In sum, the modern synthesis describes how evolutionary processes, such as natural selection, can affect a population’s genetic makeup, and, in turn, how this can result in the gradual evolution of populations and species. The theory also connects this change in gene frequencies of a population over time, called microevolution, with the processes that gave rise to new species and higher taxonomic groups with widely divergent characters, called macroevolution.

Review Question:

What is the difference between micro-and macroevolution?
A) Microevolution describes the evolution of small organisms, such as insects, while macroevolution describes the evolution of large organisms, like people and elephants.
B) Microevolution describes the evolution of microscopic entities, such as molecules and proteins, while macroevolution describes the evolution of whole organisms.
C) Microevolution describes the evolution of organisms in populations, while macroevolution describes the evolution of species over long periods of time.
D) Microevolution describes the evolution of organisms over their lifetimes, while macroevolution describes the evolution of organisms over multiple generations.

Population Genetics

Recall that a gene for a particular character may have several alleles, or variants, that code for different traits associated with that character. For example, in the ABO blood type system in humans, three alleles in the population determine the particular blood-type protein on the surface of red blood cells. Each individual in a population of diploid organisms can only carry two alleles for a particular gene, but more than two may be present in the individuals that make up the population. In the early twentieth century, biologists in a field of study known as population genetics began to study how selective forces change a population through changes in allele and genotypic frequencies.
Figure 1. Frequencies of A, B and I blood types alleles of the human population in Jordan 1998-2003

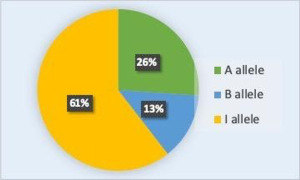
The allele frequency (or gene frequency) is the rate at which a specific allele appears within a population. This can also be thought of as the allele’s percentage in the population relative to the other alleles of that gene in the population. Until now we have discussed evolution as a change in the characteristics of a population of organisms, but behind that phenotypic change is genetic change. In population genetics, the term evolution is defined as a change in the frequency of an allele in a population (i.e. microevolution). Using the ABO blood type system as an example, the frequency of one of the alleles, IA, is the number of copies of that allele divided by all the copies of the ABO gene in the population. For example, a study in Jordan [1] found a frequency of the IA allele to be 26.1 percent. The IB and i alleles made up 13.4 percent and 60.5 percent of the alleles respectively, and all the frequencies added up to 100 percent (Figure 1). A change in this frequency over time would constitute evolution in the population.

The allele frequency within a given population can change under the following conditions: natural selection, sexual selection, genetic drift, gene flow, and mutations. The conditions are collectively called the mechanisms of evolution, specifically microevolution. If any of these mechanisms are in effect, then the population under investigation can undergo changes to its allele frequencies. For example, certain alleles may become more widespread than others through the process of natural selection. If a given allele confers a phenotype that allows an individual to better survive and/or have more offspring in a given habitat or environment. Because many of these offspring will also carry the beneficial allele, and often the corresponding phenotype, they will likely have more offspring of their own that also carry the allele, thus, perpetuating the cycle under those natural conditions. Over time, the allele will proliferate (spread) throughout the population, assuming those natural conditions remain the same (or similar). Some alleles will quickly become fixed in this way, meaning that every individual of the population will carry the allele, while deleterious (detrimental) alleles could potentially be swiftly eliminated from the gene pool, the sum of all the alleles in a population.

Review Question:

Population genetics is the study of:
A) how selective forces change the allele frequencies in a population over time
B) the genetic basis of population-wide traits
C) whether traits have a genetic basis
D) the degree of inbreeding in a population

Hardy-Weinberg Principle of Equilibrium

If you have ever endeavored to improve your performance in anything, then you probably were advised to take a baseline measurement and record your current performance. You might get your blood drawn, time laps in a pool, record weights you are lifting, record a video of a voice, instrument, or acting performance, or weigh yourself first. After some time practicing and improving, you’d record the same thing again. Without that baseline on record it is difficult to objectively measure your improvement. The same idea can be used to measure evolution. Constantly changing environments logically imply that gene frequencies are also constantly changing. The question becomes is this microevolution or just natural “noise”? To answer this, we must have a baseline, or a population that is not evolving, to which we can compare any changes.

In the early twentieth century, English mathematician Godfrey Hardy and German physician Wilhelm Weinberg formulated a mathematical principle of equilibrium that could be used to describe the genetic makeup of a population. The theorem, which later became known as the Hardy-Weinberg principle of equilibrium, states that a population’s allele and genotype frequencies are inherently stable— unless, evolutionary forces are acting upon the population, neither the allele nor the genotypic frequencies should change. If a population is in this equilibrium, then it is not evolving and therefore can be thought of as the baseline measurement. Then we can compare all changes in allele frequencies to this baseline and statistically determine if the population is evolving. The Hardy-Weinberg principle assumes conditions with no mutations, migration, emigration, or selective pressure for or against genotype, plus an infinite population. While no population can satisfy those conditions, the principle offers a useful model against which to compare real population changes. Notice these conditions negate the mechanisms of evolution previously listed and therefore we should not expect allele frequencies to change.

Review Question:

Which of the following are criteria for maintaining Hardy-Weinberg equilibrium involving two alleles for a gene? (Multiple Answer)

A) Populations must be large

B) The frequency of all genotypes must be equal
C) No mutations occur
D) No emigration or immigration

Population geneticists represent different alleles as different variables in this mathematical model. The variable p, for example, often represents the frequency of a particular allele, say the dominant Y for the trait of yellow in peas, then the variable q would represent the frequency of the recessive y alleles that confer the color green. If these are the only two possible alleles for a given locus in the population, p + q = 1 (or 100%). In other words, all the p alleles and all the q alleles make up all the alleles for that locus that are found in the population.

What ultimately interests most biologists is not the frequencies of different alleles, but the frequencies of the resulting genotypes, the population’s genetic structure allows scientists to determine the distribution of phenotypes. When it is a phenotype that can be observed, only the genotype of the homozygous recessive alleles can be known; as individuals with the dominant phenotype can be either homozygous or heterozygous for the trait. However, the use of the Hardy-Weinberg equilibrium equation can be used to calculations an estimate of the remaining genotypes. Since each individual in this model carries two alleles per gene if the allele frequencies (p and q) are known, predicting the frequencies of these genotypes is simple.

Figure 2. Genotypes and corresponding phenotypes for pea seeds.

One can easily calculate the probability of getting specific allele combinations (i.e. homozygous dominant, heterozygous, and homozygous recessive) if two alleles are drawn at random from the gene pool. So, in the above scenario, an individual pea plant could be homozygous dominant (YY, yellow peas), heterozygous (Yy, yellow peas), or homozygous recessive (yy, green peas) (Fig. 2).  If the frequency of the allele Y = p, then the probability of randomly drawing two Y’s from the gene pool is the product of each allele’s individual probabilities, or p x p = p2. This is the frequency of the homozygous dominant genotype in the population. Likewise, the frequency of y is q, and thus drawing two y’s at random is q x q = q2. This is the frequency of the homozygous recessive genotype in the population.

The heterozygous genotype can be achieved in two ways: drawing a Y and then a y, or drawing a y and then a Y. As these are two separate events, we must add each combination’s probability. First, Y then y equals p x q = pq. Second, y then Y equals q x p = qp. Combining the events: pq + qp = 2pq. This is the frequency of the heterozygous genotype in the population. In this instance, Y and y are the only two alleles in the population, therefore p2 + 2pq + q2 = 1 (or 100%) (Fig. 3).

Figure 3. Hardy-Weinberg Equilibrium Equations

So, how do population geneticists use these principles to study if the frequency of alleles for a gene in the population is changing? Let’s start with a population of peas, where we can visually count the number of yellow seeds and the number of green seeds. We discover that out of a population of 1000 individuals, 910 individuals produce yellow seeds and 90 individuals produce green seeds.  How can we determine the allele frequencies for the Y and y alleles from this information? Well, we know that the green seed individuals must be homozygous recessive (yy) and that the yellow seed individuals can be either homozygous dominant (YY) OR heterozygous (Yy).

As before, we will designate the frequency of the dominant Y allele to be p and the frequency of the recessive y allele to be q. Using the known number of green seed producers we can calculate q. Why? Because we know that all of the green seed producers have the homozygous recessive genotype.

So, frequency of yy equals q2 and thus q2 =90/1000 total or 0.09

The frequency of y = √q , in this case √.09 which is 0.3

Once we have q, we can calculate p; 1 – q = p

p = 1 – 0.3 = 0.7

Finally, the frequency of YY is p2,  in this case, 0.49 (0.72) and the frequency of Yy is 2pq (2*0.3*0.7) which is 0.42. Using these frequencies we can determine that of the 910 yellow seed producers 420 are heterozygotes (Yy) and 490 are homozygous dominant.

Review Question:

If the frequency of the dominant allele for a trait in the population is 0.57, what is the frequency of the recessive allele in the population assuming there are only two alleles for the trait?

In theory, if a population is at equilibrium—that is, there are no evolutionary mechanisms acting upon it— generation after generation would have the same gene pool and genetic structure, and these equations would all hold true all the time. Of course, both Hardy and Weinberg recognized that no natural population is immune to evolution. Populations in nature are constantly changing in genetic makeup due to genetic drift, mutation, possibly migration, and selection pressures. As a result, the only way to determine the exact distribution of phenotypes in a population is to go out and count them. What the Hardy-Weinberg principle gives scientists is a mathematical baseline of a non-evolving population to which they can compare natural populations and thereby infer if evolutionary forces might be at play. If the frequencies of alleles or genotypes deviate from the value expected from the Hardy-Weinberg equation, then the population must be evolving.

Review Question:

Which of the following populations is NOT in Hardy-Weinberg equilibrium?
A) a population with 12 homozygous recessive individuals (yy), 8 homozygous dominant individuals (YY), and 4 heterozygous individuals (Yy)
B) a population in which the allele frequencies do not change over time
C) p2 + 2pq + q2 = 1
D) a population undergoing natural selection

Summary

Modern synthesis of evolutionary theory grew out of the cohesion of Darwin’s, Wallace’s, and Mendel’s thoughts on evolution and heredity, along with the more modern study of population genetics. It describes the evolution of populations and species, from small-scale changes among individuals (microevolution) to large-scale changes (macroevolution) over paleontological time periods. By tracking changes in populations’ allele frequencies over time scientists can determine if evolutionary mechanisms are acting upon the population. The use of the Hardy-Weinberg equilibrium model can help scientists compare the natural population with a baseline. If the population’s allele frequencies differ from those predicted by the model, scientists can conclude that the population is not in Hardy-Weinberg equilibrium, and is thus evolving.

End of Section Review Questions:

Review: Microevolution vs. Macroevolution
1) Changes in _________ frequencies in a _________ over time is part of the process of microevolution.  Macroevolution focuses on changes _________ in over time.

Word Bank: mutation, species, allele, population, individual

Review: Using Hardy-Weinberg
2) In plants, violet flower color (V) is dominant over white (v). If p = 0.8 and q = 0.2 in a population of 500 plants, how many individuals would you expect to be homozygous dominant (VV)?

How many individuals would you expect to be heterozygous (Vv)?
How many individuals would you expect to be homozygous recessive (vv)?
How many plants would you expect to have violet flowers?
How many would have white flowers?

Review: Frequencies of Genotypes

3) In a Hardy-Weinberg population with two alleles, A and a, that are in equilibrium, the frequency of the recessive allele a is .7. What is the percentage of the population that is homozygous for this allele? (answer in %, not decimals)

Attribution

1 Sahar S. Hanania, Dhia S. Hassawi and Nidal M. Irshaid, 2007. Allele Frequency and Molecular Genotypes of ABO Blood Group System in a Jordanian Population. Journal of Medical Sciences, 7: 51-58. DOI: 10.3923/jms.2007.51.58

AttributionsText adapted from OpenStax Biology 2nd Edition, Biology 2e. OpenStax CNX. Nov 26, 2018 http://cnx.org/contents/8d50a0af- 948b-4204-a71d-4826cba765b8@15.1.

Figure 1. Courtesy of D. Jennings CC By 4.0

Figure 2. Courtesy of D. Jennings CC By 4.0

Evolution Connection: 

Evolution and Flu Vaccines

Every fall, the media starts reporting on flu vaccinations and potential outbreaks. Scientists, health experts, and institutions determine recommendations for different parts of the population, predict optimal production and inoculation schedules, create vaccines, and set up clinics to provide inoculations. You may think of the annual flu shot as a lot of media hype, important health protection, or just a briefly uncomfortable prick in your arm. But do you think of it in terms of evolution?

The media hype of annual flu shots is scientifically grounded in our understanding of evolution. Each year, scientists across the globe strive to predict the flu strains that they anticipate being most widespread and harmful in the coming year. This knowledge is based in how flu strains have evolved over time and over the past few flu seasons. Scientists then work to create the most effective vaccine to combat those selected strains. Hundreds of millions of doses are produced in a short period to provide vaccinations to key populations at the optimal time.

Because viruses, like the flu, evolve very quickly (especially in evolutionary time), this poses quite a challenge. Viruses mutate and replicate at a fast rate, so the vaccine developed to protect against last year’s flu strain may not provide the protection needed against the coming year’s strain. The evolution of these viruses means continued adaptions to ensure survival, including adaptations to survive previous vaccines.

definition

License

Icon for the CC0 (Creative Commons Zero) license

To the extent possible under law, s2jrmoor has waived all copyright and related or neighboring rights to VCU BIOL 152: Introduction to Biological Sciences II, except where otherwise noted.

Share This Book