Introduction

Among the umbrella of numerous learning disabilities that children may be diagnosed with, dyscalculia is one of the lesser-known ones that is misunderstood and lacks research (Price & Ansari, 2013). A student who has a math learning disability (MLD) or dyscalculia has “significant difficulty learning mathematics” (Lambert, 2024, p. 25). Educators in K12 classrooms aiming to offer inclusive math learning activities to increasingly diverse learners are challenged to offer learning experiences for all learners, including students with dyscalculia. This chapter will discuss some of the barriers for students who have dyscalculia, as well as provide an overview of universal design of learning (UDL) strategies for educators to enhance the math learning opportunities for students with dyscalculia.

First, let us define dyscalculia. Developmental Dyscalculia is a learning disorder that hinders the development of basic math skills, affecting roughly 3-6% of the population (Butterworth et al., 2011; Price & Ansari, 2013; Shalev, 2007). It is recommended that a child is diagnosed, according to the Diagnostic and Statistical Manual of Mental Disorders (DSM-IV) when “mathematical ability, as measured by individually administered standardized tests, is substantially below that expected given the person’s chronological age, measured intelligence, and age-appropriate education” (as cited in Price & Ansari, 2013, p.1). According to the website Dyscalculia.org (n.d.), dyscalculia is characterized by challenges in counting, working memory, and visualization, as well as difficulties with visuospatial awareness, directionality, and sequential processing. Individuals may also struggle with retrieving learned facts and procedures, processing quantitative reasoning quickly, motor sequencing, time perception, and accurately interpreting and representing numbers in activities like reading, copying, writing, reasoning, and speaking. Geary (2011) explains that mathematical learning disabilities are often rooted in deficits in numerical processing, working memory, and visuospatial skills. According to Butterworth (2010), specific challenges include mathematical representations and symbolism, such as making connections between numbers and amounts or perceiving quantity.

Dr. Daniel Ansari of the University of Western Ontario provides an overview of dyscalculia in the video, What is Dyscalculia (Numerical Cognition Laboratory, 2014). The video explains that dyscalculia is a math-specific learning difficulty, especially with understanding numbers and how they relate to quantity. It is compared to dyslexia, but for math, and is not as well understood or supported. The video also mentions that students with dyscalculia may find it harder to make sense of sizes, shapes, and space, and often have trouble remembering basic math facts.

Accessibility Issues & Barriers for Students with Dyscalculia

Students who struggle with developing foundational number sense may have challenges in classrooms where the teacher has designed learning activities based on the neurotypical or “average” student and has not considered the students’ learning differences. This is true for many students with learning disabilities. Identifying and understanding the existing challenges is essential for making the learning accessible to all students (Lambert, 2024). Additionally, children with developmental dyscalculia are twice as likely to experience high mathematics anxiety compared to those with typical math performance (Devine et al., 2018). Students with dyscalculia face numerous barriers in standard K12 settings. Key challenges emerge in math curriculum design, classroom instruction, assessment practices, and teacher preparedness. These factors can leave dyscalculic learners struggling to keep up and not receive the needed support.

Curriculum Design

Math curricula often assume that all students will master concepts like arithmetic or fractions within a set timeframe, but for students with dyscalculia, this pace is unmanageably fast (Pagliaro-Newman, 2024). Without a structured, spiralling curriculum that revisits foundational concepts, these learners struggle to retain foundational knowledge and often forget previously learned skills. Compounding these difficulties, many curricula introduce abstract concepts (like algebra or complex word problems) before students have mastered the necessary basic skills. Research suggests that these students benefit from a gradual progression from concrete examples and representations before moving on to abstract concepts (Napolitano, 2025). In Ontario, the mathematics curriculum emphasizes the importance of foundational number sense and revisiting concepts through spiralled instruction (Ontario Ministry of Education, 2023). Traditional math programs often focus on memorizing facts quickly, which is especially challenging for learners who rely on counting strategies due to difficulties with recall. In the absence of alternative approaches, this emphasis on speed and rote learning can lead to anxiety and widen achievement gaps for students with dyscalculia.

Classroom Instruction and Assessment Practices

Inclusive pedagogical practices are paramount for students with disabilities, and in particular, for students with dyscalculia. When classroom instruction is not designed with the strengths of all students in mind, not all students will have a chance at being successful. Differentiation for these students is essential as traditional teaching methods may not meet their needs. Lambert’s (2024) Universal Design for Learning in Mathematics (UDL Math) will be discussed later in the chapter, and it aims to broaden a teacher’s mindset in planning for instruction that impacts three areas of learning identified by Meyer et al. (2014): engagement, representation, and strategic action.

Regarding assessment practices, Lambert (2024) also identifies that rigid assessment formats are often rooted in ableist assumptions about how learning should look, especially in mathematics. Timed, paper-and-pencil assessments, such as quizzes, tests, and exams, are especially challenging for students with dyscalculia due to difficulties with executive function and working memory. These challenges can make it harder to follow multi-step problems, retain sequences, and retrieve basic facts (Cowan, 2010). As a result, differentiated assessments that align with students’ strengths are essential for providing equitable opportunities to demonstrate understanding.

Teacher Preparedness

Given that the research about supporting students with dyscalculia is lacking (Price & Ansari, 2013; Pagliaro-Newman, 2024), educators are not necessarily prepared to effectively support the diverse strengths and needs of their students with dyscalculia. “Consequently, students with dyscalculia are not getting the support they need, due to the lack of teachers’ knowledge about the disorder” (Pagliaro-Newman, 2024). Lambert (2021) suggests that there is a need to shift from deficit-based pedagogy to asset-based, where the students’ strengths are built upon, which is the basis for UDL and can be most effective in supporting all students. Additionally, teachers’ and students’ beliefs, attitudes, and emotions can influence how mathematics is approached in the classroom, potentially reinforcing barriers to learning when left overlooked (De la Oliva, 2020, as cited in Espina, Marbán, & Maroto, 2024).

Student Impact of Dyscalculia

As an educator, considering the student voice is an important aspect of improving instruction and outcomes, as it puts the student at the centre of the work. The personal impact of dyscalculia is as important as the academic barriers and recommendations previously mentioned. Students’ engagement and confidence can be affected if they are internalizing their mathematical difficulties. One educator and researcher who has written extensively about math identity and student mindset is Jo Boaler, whose work focuses on helping all students see themselves as capable math learners. Boaler (2016) highlights how early struggles in math can lead students to believe they are not “math people,” which can affect their confidence and willingness to engage. This fixed mindset can develop over time, especially for students with dyscalculia who face repeated challenges in traditional math classrooms. Additionally, students may feel frustration, anxiety, and a sense of failure when they cannot understand mathematics like their peers. Espina, Marbán, and Maroto (2024) conducted a systematic review that found that while math anxiety is well-researched, a broader range of emotional challenges is often overlooked in both research and classrooms, such as negative beliefs about ability and low self-concept. Their review revealed that more research is needed related to the affective domain for students with dyscalculia beyond the larger focus of math anxiety. A recent case study of a student named Nur further illustrates how the challenges of dyscalculia can extend beyond academics. Nur reported a loss of self-confidence, feelings of isolation, and difficulty managing daily tasks that involved numbers—highlighting how dyscalculia can impact social and emotional well-being as well as long-term personal and professional development (Baykal & Durmuş, 2025). Educators would benefit from understanding the personal perspectives and attitudes of students with dyscalculia and building on their instructional strategies to empower all students to succeed in mathematics.

Inclusive Design Recommendations

The focus of the inclusive design recommendations presented in this section will be based on Rachel Lambert’s (2024) Universal Design for Learning in Math (UDL Math) from her recent book, Rethinking Disability and Mathematics: A UDL Math Classroom Guide for Grades K-8. She premised the approach for math class on UDL, designed by CAST (Meyer et al., 2014), an educational framework that provides flexible learning environments to accommodate diverse student needs through multiple means of representation, engagement, and expression. This emphasis on proactive, inclusive design is also reflected in the Ontario mathematics curriculum, which encourages educators to remove barriers and support a wide range of learners through flexible instruction and assessment strategies (Ontario Ministry of Education, 2023). Lambert does not see UDL as another educational framework but “as a ‘way to move,’ a way to notice what is not working for our students (barriers), and to creatively open up our classrooms so that more students can be successful” (Lambert, 2024, p. 75).

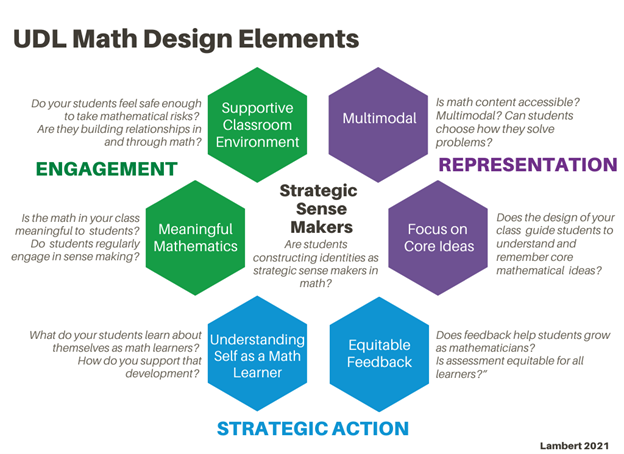
Lambert (2021) outlines six important elements to consider when planning and creating accessible mathematics experiences for students. They are shown in Figure 1 and will be explored in the following paragraphs, along with the guiding questions listed within the figure.

Meaningful Mathematics

Lambert (2024) provides these guiding questions: “Is the math in your class meaningful to students? Do students regularly engage in sense-making?” Students consistently need math experiences that are meaningful and engaging, and that challenge students when solving problems.

Supportive Classroom Environment

Lambert (2024) provides these guiding questions: “Do your students feel safe enough to take mathematical risks? Are they building relationships in and through math?” A safe environment goes a long way in providing an optimal learning space for learning mathematics. We want students to feel confident and not anxious about taking risks when solving problems in math, which is about thinking and collaborating, not competition or perfection.

Multimodal

Lambert (2024) provides these guiding questions: “Is math content accessible? Multi-modal? Can students choose how they solve problems? Are representations connected to each other? To concepts?” Students will access math through various connected representations, which is necessary for students with sensory disabilities. Math content should be presented using representations such as, but not limited to, drawings, number lines, graphs, equations, expressions, and visual patterns. Allow students to choose what representation makes sense to them.

Invest Time in Core Ideas

Lambert (2024) provides these guiding questions: “Does the design of instruction guide students to understand core mathematical ideas? Mathematical representations? Develop strategies?” Educators need to focus on students learning the core ideas, and value speed much less than it has traditionally. Students would benefit from having time to learn the math deeply, in a conceptual way, through multiple learning opportunities. Some students will need more time to build knowledge and skills conceptually.

Equitable Feedback

Lambert (2024) provides these guiding questions: “Does feedback help students grow as mathematicians? Is assessment equitable for all learners?” Assessment needs to be focused on understanding student learning and not discriminate against students with disabilities by having timed assessments. Excessive and unhelpful assignments are also barriers for students with disabilities; therefore, differentiated assessments are beneficial if they are responsive to the individual learner.

Understanding Self as a Math Learner

Lambert (2024) provides these guiding questions: “What do your students learn about themselves as math learners? How do you support strategic development?” We want students to understand who they are as math learners and, in turn, be able to self-advocate for their needs. Educators can help students understand their strengths and areas where they need more support by having regular conversations with them.

Further Exploration of Dyscalculia

Provided below are additional resources, including a video about supporting students with dyscalculia in K12 education.

Shining a Light on Dyscalculia

Dawn Pagliaro-Newman’s article, Shining a Light on Dyscalculia, emphasizes the importance of recognizing and understanding dyscalculia, a neurodivergent condition affecting mathematical learning. She highlights that, unlike dyslexia, dyscalculia has received less research and fewer resources, leading to a lack of teacher preparation in supporting affected students. The article outlines specific indicators of dyscalculia, such as difficulty with number patterns and subitizing, and advocates for structured, multisensory teaching approaches to support these learners effectively.

The Math is in the Margins: UDL Math

Rachel Lambert’s article, The Math is in the Margins: UDL Math, was published in 2021 in the NCTM’s Mathematics Teacher: Learning and Teaching PK12. Lambert discusses how Universal Design for Learning (UDL) can transform math teaching by focusing on the needs of marginalized students. She highlights the importance of designing math instruction that accommodates diverse learners and plays to their strengths. Lambert encourages educators to rethink their practices in ways that make math more inclusive, flexible, and accessible for all students.

Invest in Tier 1: Designing from the Margins with UDL Math

In the Invest in Tier 1: Designing from the Margins with UDL Math session presented by Rachel Lambert, Ph.D., the focus is on designing mathematics instruction from the perspective of marginalized learners. The session explores designing math classrooms through Universal Design for Learning (UDL), focusing on supporting dyslexic students. It emphasizes shifting from a deficit-based approach to one that leverages student strengths, offering valuable insights for creating inclusive, flexible learning environments for all students, including those with dyscalculia.

Conclusion

As Rachel Lambert emphasizes, the goal is not to fit students into the existing structure of math education, but to redesign that structure so all students can thrive. Supporting students with dyscalculia demands a shift away from deficit thinking and toward inclusive, strength-based practices rooted in UDL. When educators reimagine mathematics through this lens and by planning with all students in mind, they actively reduce barriers and create meaningful access to learning. It is a teacher’s professional responsibility to design math classrooms where every student has the opportunity to develop confidence, build a positive identity as a math learner, and experience success in learning mathematics.

References

Baykal, N., & Durmus, E. (2025). Effects of dyscalculia on personal, social, academic, professional and daily life: A case study. Journal of Pedagogical Research, 9(1), 1–15. https://doi.org/10.33902/JPR.202410942

Boaler, J. (2016). Mathematical mindsets: Unleashing students’ potential through creative math, inspiring messages and innovative teaching. Jossey-Bass.

Butterworth, B. (2010). Foundational numerical capacities and the origins of dyscalculia. Trends in Cognitive Sciences, 14(12), 534–541. https://doi.org/10.1016/j.tics.2010.09.007

Butterworth, B., Varma, S., & Laurillard, D. (2011). Dyscalculia: From brain to education. Science (American Association for the Advancement of Science), 332(6033), 1049–1053. http://www.jstor.org/stable/27977939

Cowan, N. (2010). The magical mystery four: How is working memory capacity limited, and why? Current Directions in Psychological Science : A Journal of the American Psychological Society, 19(1), 51–57. https://doi.org/10.1177/0963721409359277

Devine, A., Hill, F., Carey, E., & Szucs, D. (2018). Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. Journal of Educational Psychology, 110(3), 431–444. https://doi.org/10.1037/edu0000222

Dyscalculia.org. (n.d.). [Home page]. https://www.dyscalculia.org/home

Espina, E., Marbán, J. M., & Maroto, A. (2024). The affective domain in mathematics in children with dyscalculia: A systematic review. Quadrante: Revista de Investigação em Educação Matemática, 32(2), 106–129. https://doi.org/10.48489/quadrante.38689

Geary, D. C. (2011). Cognitive predictors of achievement growth in mathematics: A five-year longitudinal study. Developmental Psychology, 47(6), 1539–1552. https://doi.org/10.1037/a0025510

Lambert, R. (2021). The magic is in the margins: UDL math. Mathematics Teacher: Learning and Teaching PK12, 114(9), 660–669. https://doi.org/10.5951/MTLT.2020.0282

Lambert, R. (2024). Rethinking disability and mathematics: A UDL math classroom guide for grades K–8. Corwin Press.

Meyer, A., Rose, D. H., & Gordon, D. T. (2014). Universal design for learning: Theory and practice. CAST Professional Publishing.

Napolitano, J. (2025, January 22). Teachers join forces to understand dyscalculia, a math-related learning disorder. The 74. https://www.the74million.org/article/teachers-join-forces-to-understand-dyscalculia-a-math-related-learning-disorder/

Numerical Cognition Laboratory. (2014, March 14). What is Dyscalculia? [Video]. YouTube. https://www.youtube.com/watch?v=imhRoqxSEhU

Ontario Ministry of Education. (2023). The Ontario curriculum: Mathematics, grades 1–8 (revised). https://www.dcp.edu.gov.on.ca/en/curriculum/elementary-mathematics

Pagliaro-Newman, D. (2024, April 25). Shining a light on dyscalculia. Edutopia. https://www.edutopia.org/article/teaching-students-dyscalculia/

Price, G. R., & Ansari, D. (2013). Dyscalculia: Characteristics, causes, and treatments. Numeracy, 6(1), Article 2. https://doi.org/10.5038/1936-4660.6.1.2

Shalev, R. S. (2007). Prevalence of developmental dyscalculia. In D. B. Berch & M. M. M. Mazzocco (Eds.), Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities (pp. 49–60). Paul H. Brookes.