"

Topic 5 – Gable Ends, Studs, and Ladders

Gable Studs (Run x Rise)

Much like common rafters, we calculate theory lengths of gable studs. It is measured from the top plate to the theory line of the common rafter and is calculated using units of run and unit rise. The formula for calculating the line length of a gable stud is straightforward:

L i n e L e n g of t h o f G of a. b l e S t u d equals R u n o f S t u d open paren f of e e t close paren times U n i t r i s e open paren i n c h of e s close paren

The run of the gable stud is equal to the distance from the nearest exterior wall in decimal feet.

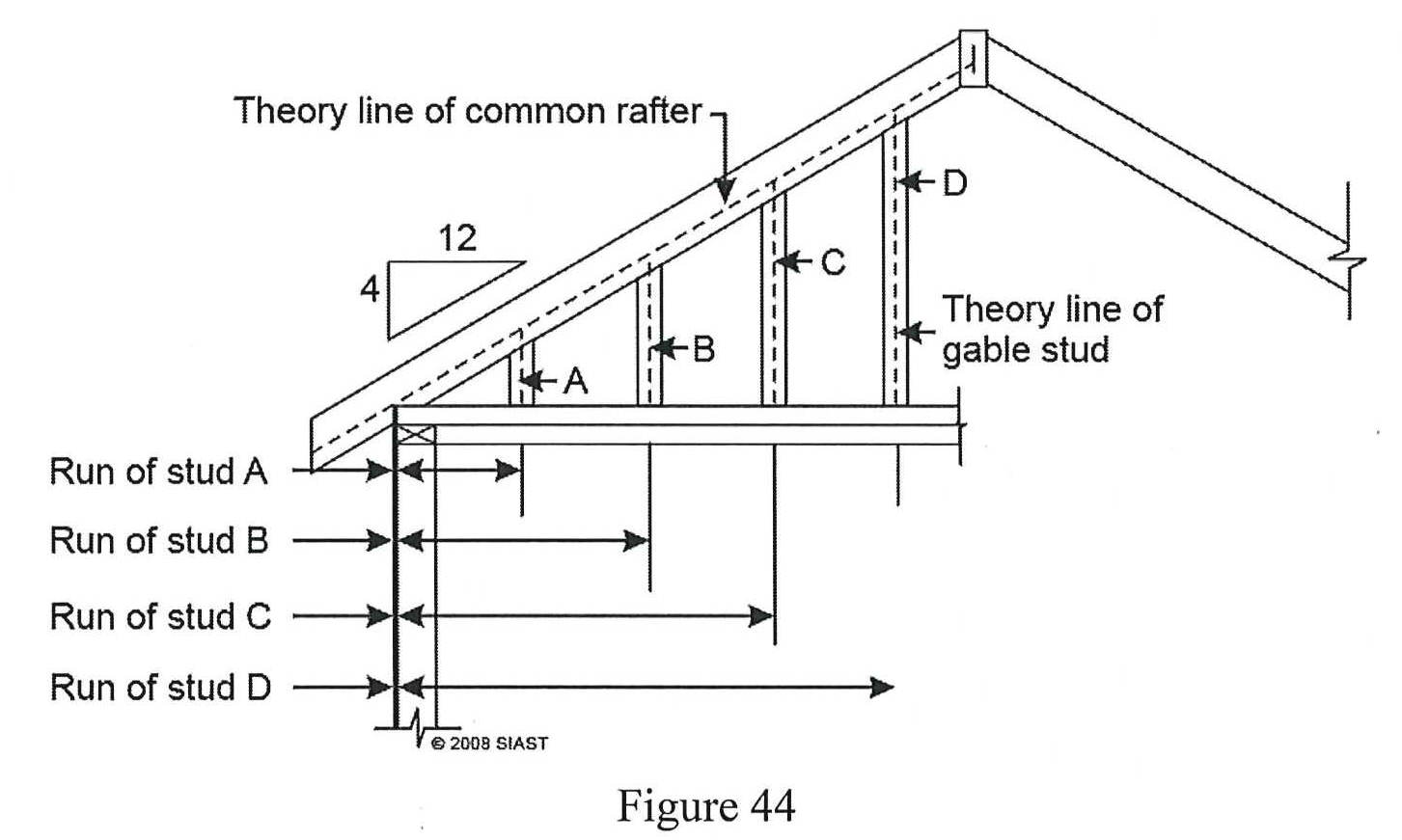
image

For example, let’s say in figure 44 above, stud C is 6’-0” from the exterior wall:

L i n e L e n g of t h o f S t u d C equals 6 open paren u n i t s o f r u n close paren times 4 quotation mark open paren u n i t r i s e close paren equals 24 quotation mark

Gable Studs (Common Difference)

We can also find lengths of gable studs using common difference, which is the difference between adjacent studs. To do this, we need to find how much a roof rises over each spacing. For example, let’s say we have a gable end on a 5/12 sloped roof, with gable stud spacing of 16”. The common difference between the two would be:

G of a. b l e S t u d C o m m o n D i f of f of e r e n c e equals O period C period s p a. c i n g open paren d e c i m a. l f of e e t close paren times u n i t r i s e equals open paren 16 division sign 12 close paren times 5 equals 1.33 times 5 equals 6.65 prime prime o r 6 five eighths prime prime

This method can be used to simply subtract or add the common difference to find each subsequent stud after finding the longest or shortest gable stud.

The actual length of gable studs is dependent on its orientation, supported load, and method of framing. For more information, see chapter 46 of Carpentry.

Roof Ladder

Ladders typically come prefabricated and rest on the gable studs which may or may not contain a top plate. Required on overhangs greater than 16”, it is composed of three primary parts:

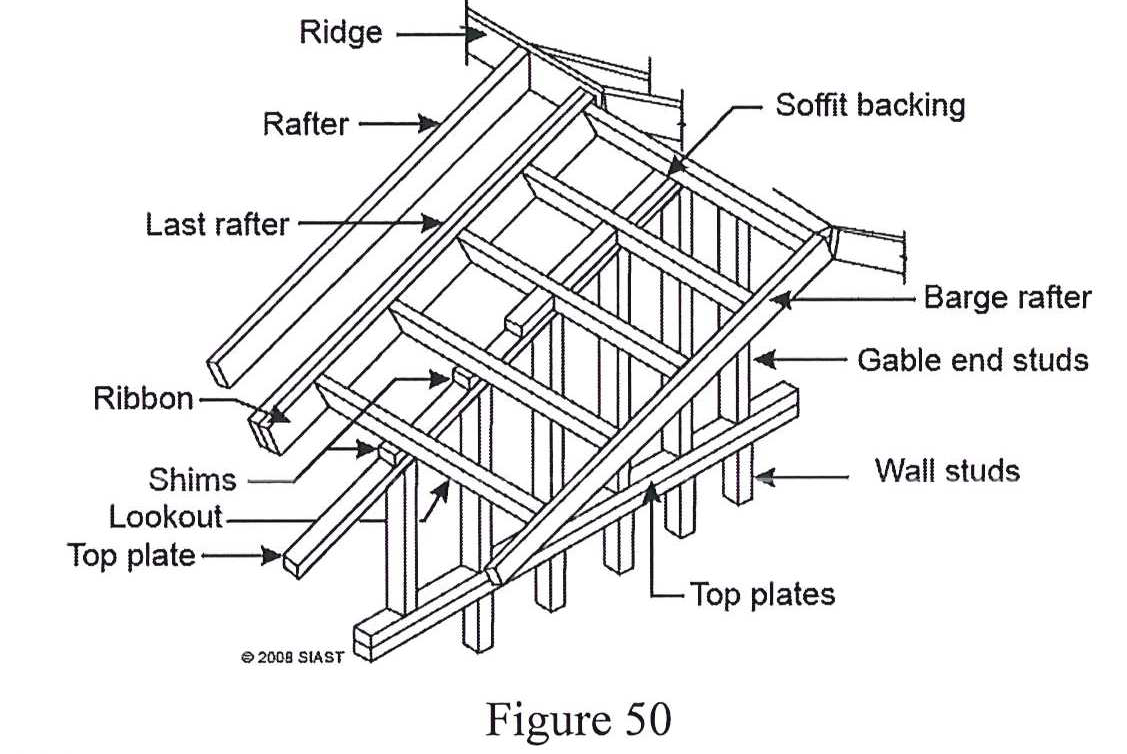
image

– Ribbon – may or may not be used, it is typically made from 19 mm stock and ties the lookouts to the first rafter
– Lookouts – usually 38 x 89 stock that rests on edge and spaced 16-24” O.C., it is the part that is cantilevered over the gable end wall and holds up the barge rafter
– Barge rafter – the outermost portion of the ladder, it acts as both the “plate” of the lookouts and rough fascia for the roof at the gable end

The lengths of the lookouts can be calculated by adding the overhang to the rafter spacing. From there, deductions are made, which may include the following if present:

– Barge rafter (typically 1 ½”)
– ½ thickness of common rafter (3/4”)
– Full thickness of the ribbon (if used, typically 3/4”)

For example, we can calculate the lengths of lookouts for the following:

– 24” overhang, 2×4 rafters spaced 16” O.C.
– 2×6 barge rafter, 1×4 ribbon
  • L o o k o u t s prime l e n g of t h equals open paren 24 right double quotation mark positive 16 right double quotation mark close paren minus open paren three fourths right double quotation mark positive three fourths right double quotation mark positive 1 and one half right double quotation mark close paren equals 40 right double quotation mark negative 3 right double quotation mark equals 37 right double quotation mark

Review Questions

  1. Find the lengths of the following gable studs:

Slope

Run

Line Length of Gable Stud

1:2.4

4’-0”

1:2

12’-0”

1:1.71

7’-6”

1:1.33

12’-6”

1:3

14’-0”

1:4

9’-0”

1:1.5

10’-6”

  1. Find the common difference in the following table:

Slope

O.C. Spacings

Difference in length Gable

1:2.4

16”

1:2

24”

1:1.71

12”

1:1.3

16”

1:3

24”

1:4

12”

1:1.5

16”

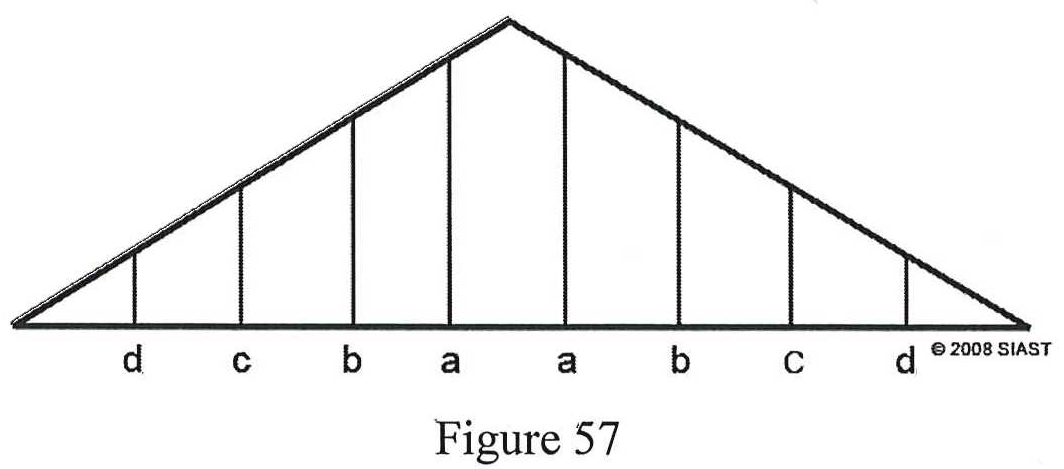
  1. Calculate the theory length of the gable studs in the following roof (figure 57). The building is 12’-0” wide, the studs are spaced 16” O.C. The layout is offset from the center 8” each way. The roof slope is 1:2.4.

image

  1. Calculate the theory length of the second longest gable stud for the following building:
– Building 24’-0” x 30’-0”
– Roof Slope 4/12
– Gable studs 24” O.C.
– Layout of studs starts at corner of building
  1. What does a roof ladder consist of?
  2. Where does the spacing of the lookouts begin?
  3. Calculate the length of the lookouts:
– 24” overhang
– 2×4 rafters 24” O.C.
– 2×6 barge rafter with 2×4 ribbon
Answer:
Slope Run Line Length of Gable Stud
1:2.4 4’-0” 1’-8”
1:2 12’-0” 6’-0”
1:1.71 7’-6” 4’-4 ½”
1:1.33 12’-6” 9’-4 ½”
1:3 14’-0” 4’-8”
1:4 9’-0” 2’-3”
1:1.5 10’-6” 7’-0”
Slope O.C. Spacings Difference in length Gable
1:2.4 16” 6 11/16”
1:2 24” 12”
1:1.71 12” 7”
1:1.3 16” 12”
1:3 24” 8”
1:4 12” 3”
1:1.5 16” 10 11/16”
  Line Length of Gable Stud
Longest Stud 2’-2 5/8”
2nd Longest Stud 1’-8”
3rd Longest Stud 1’-1 3/8”
Shortest Stud 6 5/8”
  1. 3’-2 3/8”
  2. Lookouts and barge rafter (and ribbon)
  3. At the bottom on the outside of the rough fascia
  4. 43 ½”

License

Icon for the Creative Commons Attribution 4.0 International License

Carpentry Refresher Program Manual Copyright © by Saskatchewan Indian Institute of Technologies-Trades and Industrial is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book