Topic 6 – Shed Roof Rafters

Theory Length of Shed Rafter

The line length of shed rafters is measured from birdsmouth to birdsmouth. Given the top birdsmouth rests on the inside face of the upper wall, the total run is calculated by subtracting one wall thickness (framing and sheathing) from the building width:

Run of Shed Rafter = Building Width −1 Wall Thickness

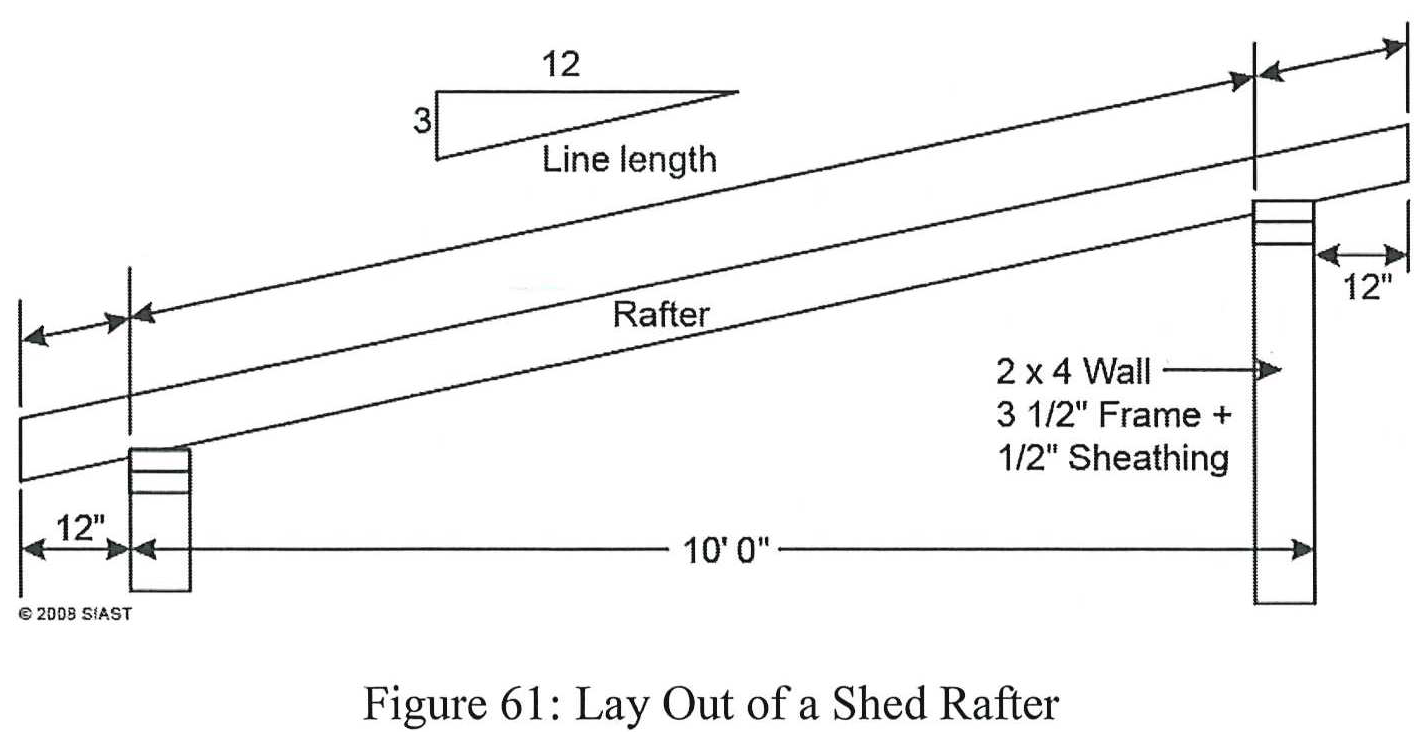
In the above example, the total run of the shed rafter would be as follows:

After finding the total run, we can calculate the line length of the shed rafter (ULL for 3/12 = 12.37”):

The bottom rafter tail is calculated the same way as common rafters:

The upper rafter tail is done differently. Because the birdsmouth begins on the inside of the upper wall, we must include the wall thickness in the run of the upper rafter tail:

Line Length of a Shed Rafter When Slope is Unknown

In situations where the slope is unknown, it is possible to calculate and layout a shed rafter using the difference in wall heights and the Pythagorean’s theorem. We will use figure 62 (below) as an example:

When using Pythagorean’s theorem (the square root method), we need to use total rise and total run. In the example above, total rise is given as 12”; we must use feet so we will use 1’ as total rise. The total run, as in the example on the previous page, is the building width minus one wall thickness. We will assume ½” sheathing on the 2×4 wall:

The slope can also be calculated using the total rise and total run. In this case, the roof rises 1’ in 7.67’, which can be expressed as a 1/7.67 slope. To convert this to a value over 12, we will use slope ratio calculations as detailed on page 56:

This means we have a roof slope of 1.56/12 which can be simplified to the nearest half inch. As a result, we have a 1.5/12 roof slope.

The rafter tails can then be calculated using the same methods as outlined in the previous page.

Review Questions – 13.01.6

1. Calculate the following using the information below:
   1. Line length of shed rafters
   2. Line length of overhang (top and bottom)

• Building 12 feet wide w/ shed roof
• 4/12 roof slope
• 12” overhang
• 5 ½” studs, ½” sheathing

2. Calculate the following using the information below:

1. 1. Line length of shed rafters
   2. Slope of shed roof
   3. Line length of overhang (top and bottom)

• Building 9’-6” wide
• 8” overhang
• Upper wall 48” higher than lower wall
• 2×4 studs and ½” sheathing

Answer:

1. 1. 12’-1 ½”
   2. Bottom – 12.65” or 1’-0 5/8” Top – 13.18” or 1’-1 3/16”

2. 1. 10’-0”
   2. 5/12
   3. Bottom – 8.71” or 8 11/16” Top – 13” or 1’-1”