Topic 8 – Ridge Boards and Hip Rafters
Ridge Board for Hip Roofs
The first step in calculating the length of the ridge board is to find its theory length. This is calculated by simply taking the building length and subtracting the building width from it. Because the ridge is terminated inside the building perimeter, we do not take the overhang into account when doing calculations involving the ridge:
Theory Length of Hip Ridge Board = Building Length − Building Width
For example, if we have a building that is 24’-0” x 36”-0”, the theory length of the ridge board would be as follows:
Theory Length of Ridge = 36′ – 24’= 12′
Actual Length of Ridge Board
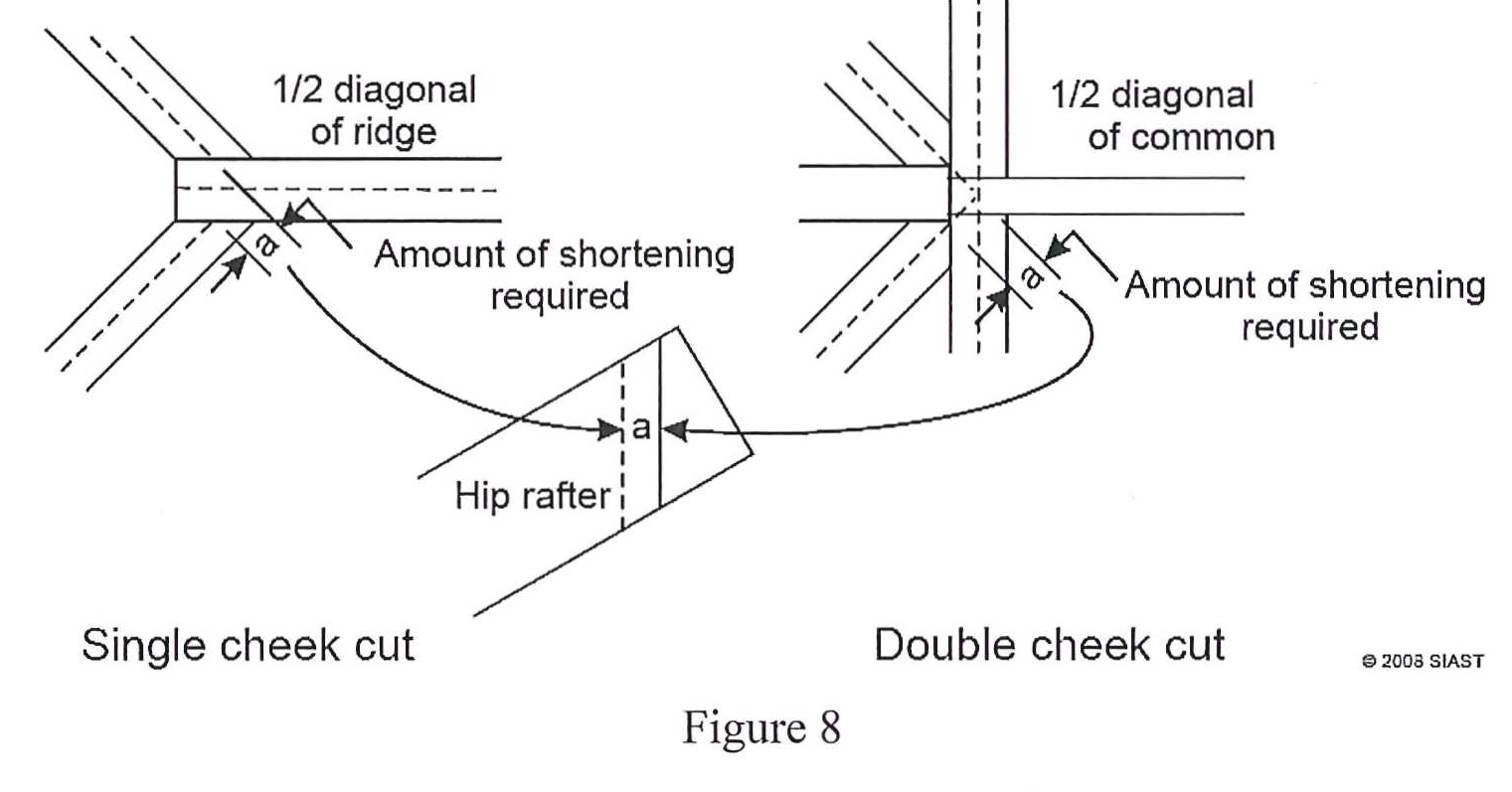
The actual length for a ridge board in a hip roof is dependent on which method is used for cutting the hip rafters. Where and how the hip intersects the ridge will change its length. There are two methods used, both of which require additions to be made to the theory length of the ridge board:
- ½ the 45° thickness of the hip rafter
- ½ the 90° thickness of the ridge board
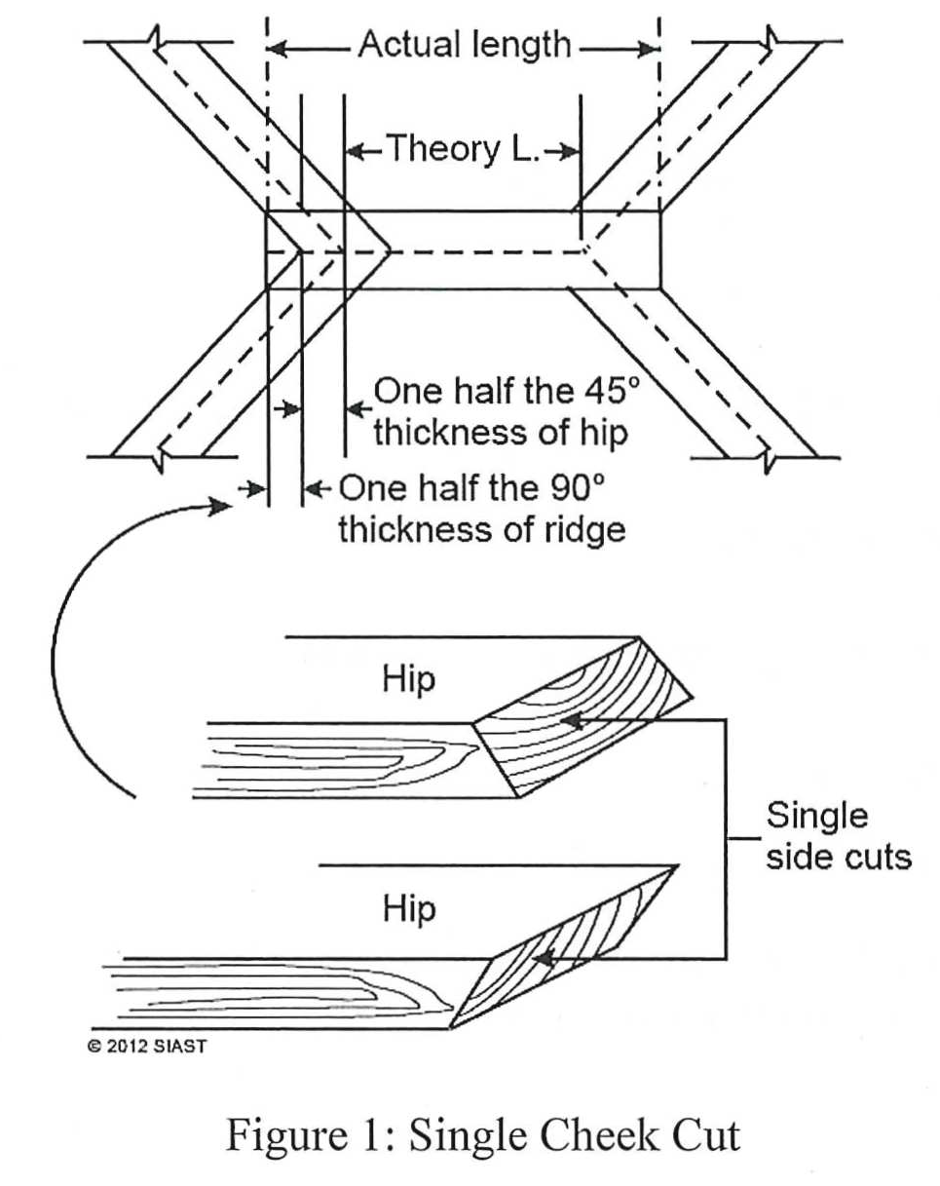
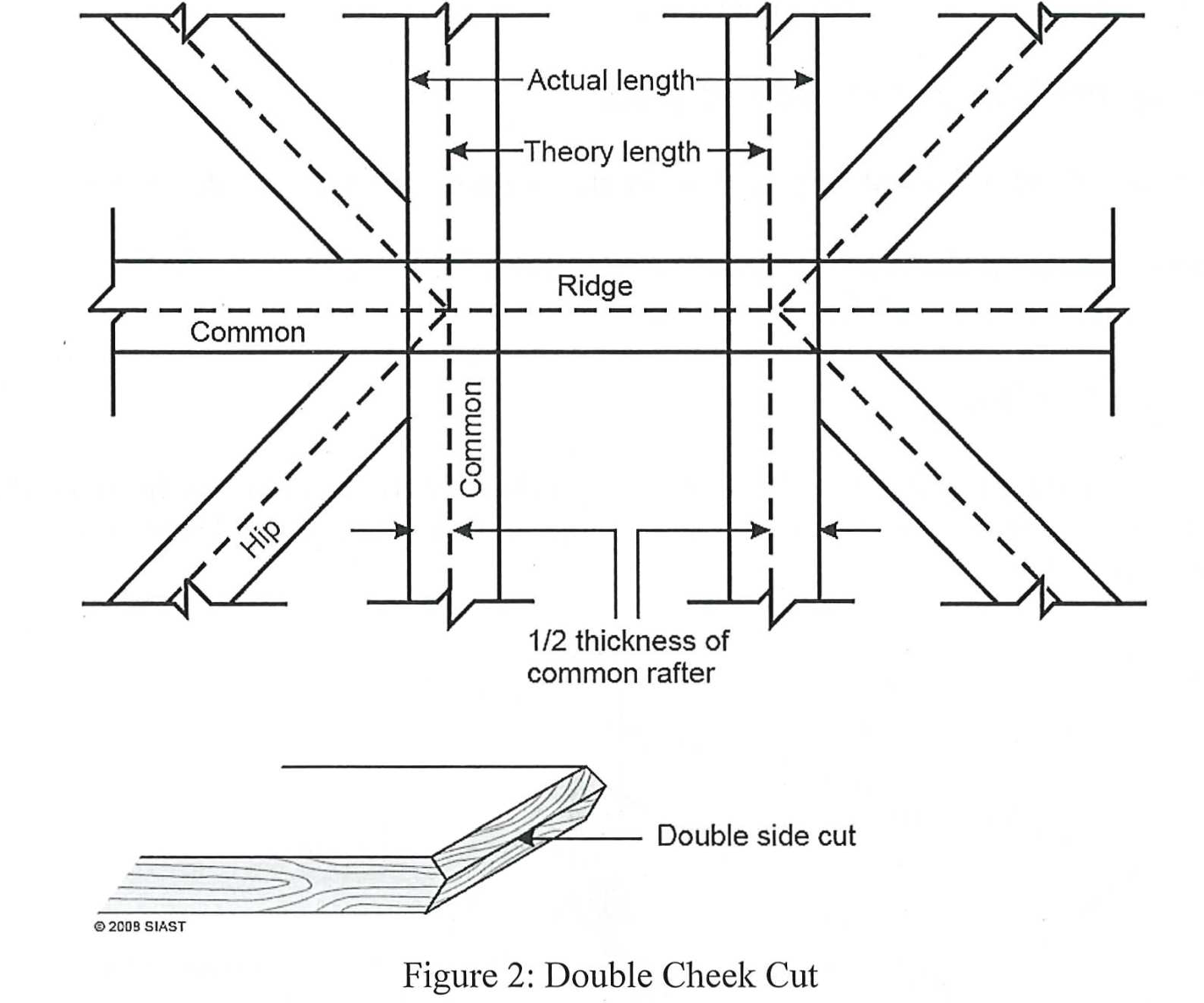
***Try to calculate the actual length of the ridge board for the following building using both methods:
- Building 26’-0” x 42’-0”
- 2×10 ridge board
- 2×8 hip rafters
- 2×6 common rafters
Line Length of Hip Rafters
There are two methods used when calculating the line length of the hip rafter:
Square Root Method
This method uses the total rise and total run of a hip rafter to calculate its line length. Just as for common rafters, we take these values and place them in Pythagorean’s theorem, where a = total rise, b = total run, and c = line length of hip rafter:
The total rise is the same as for the common rafters and can be found by multiplying the units of run times the unit rise.
The total run involves a bit more work. If we look at how the hip rafter approaches the ridge at a 45° angle, it forms an equilateral triangle with the exterior wall and common rafter (see figure 3 below). As this means both sides of this triangle are equal, we can use the total run of a common rafter to find the run of the hip rafter using Pythagorean’s theorem again:
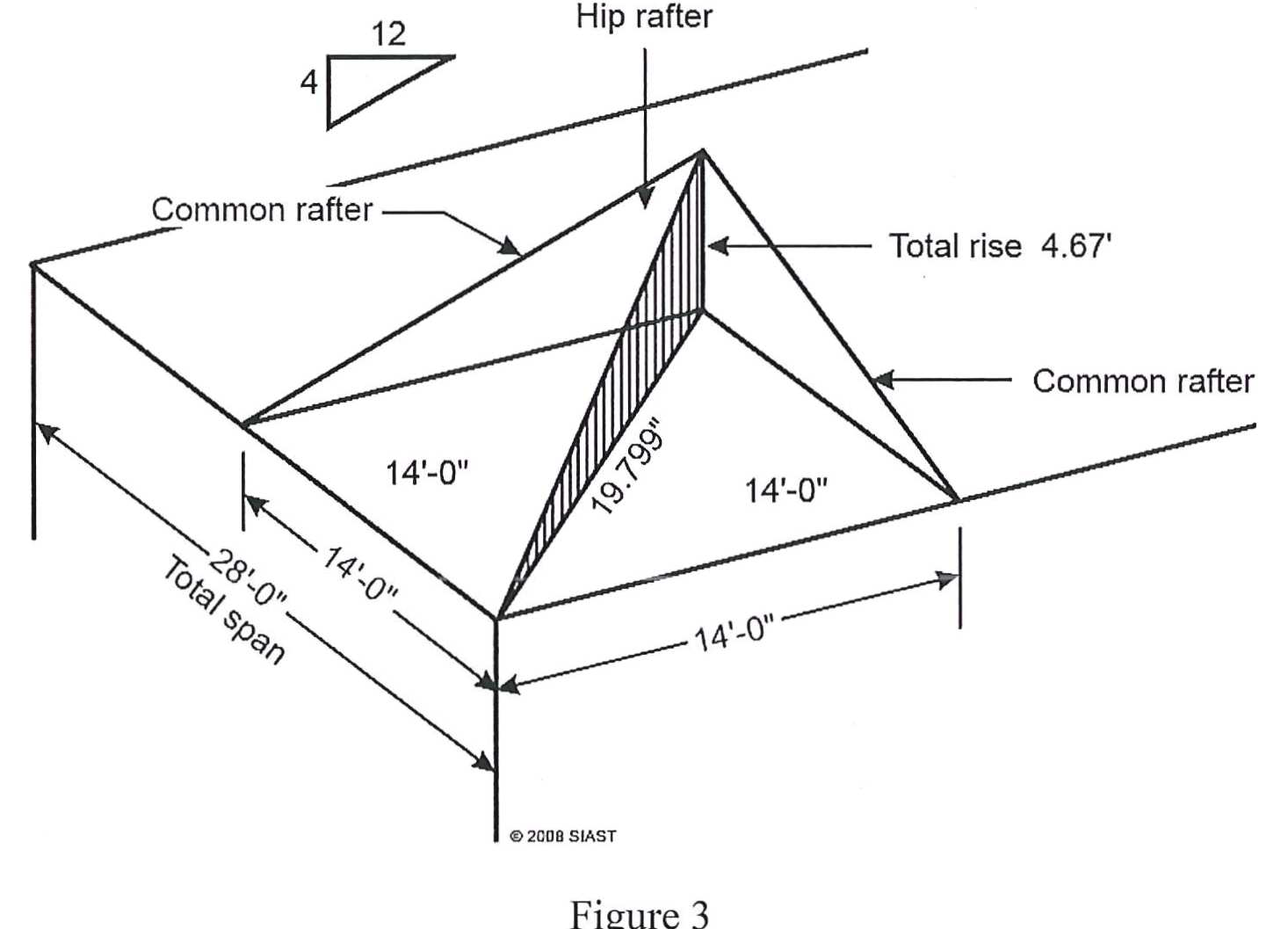
In figure three above, the total run of the hip rafter is given; we can double check this using the formula above:
Now that we have the total run and the total rise, we can find the line length of the hip rafter in figure 3:
Unit Line Length
We can also find the line length of hip rafters using unit line length (ULL). This unit line length can be calculated or found on certain framing squares. While finding the ULL is an extra step, this method is advantageous as it allows us to use the same amount of units of run as the common rafters.
For common rafters, the unit run is always 12”. Because hip rafters run at 45° to the common rafters, the unit run must be altered to accommodate the gain in length run in relation to the common rafters (see figure 4 below). We can calculate the unit run by again using Pythagorean’s theorem:
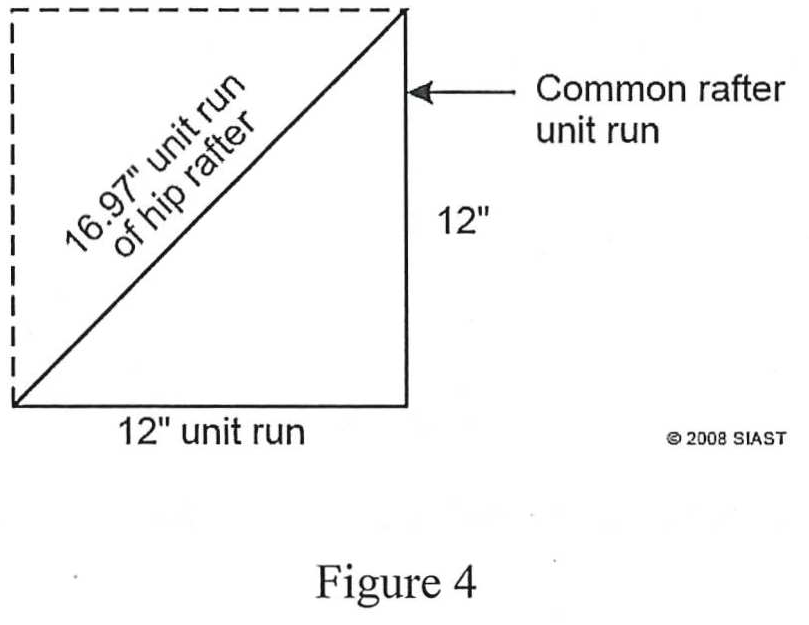
When laying out hip rafters with a framing square, this value is rounded up to 17” and the unit rise remains constant. For calculating the ULL, we must use 16.97” as the unit run. For example, we will use the roof illustrated in figure 3 (4/12 slope):
Again using figure 3, we can use the unit line length to find the line length of the hip rafter. Notice how the amount of units of run does not change from common to hip rafters:
Rafter Tails
We can also use the unit line length to find the lengths of hip rafter tails. We will use the ULL calculated in the previous step with a 2’-0” overhang. Just like with common rafters, the amount of units of run is equal to the total run in decimal feet:
Deductions for Hip Rafters
The deduction made at the top of the hip rafter is dependent on which method is used:
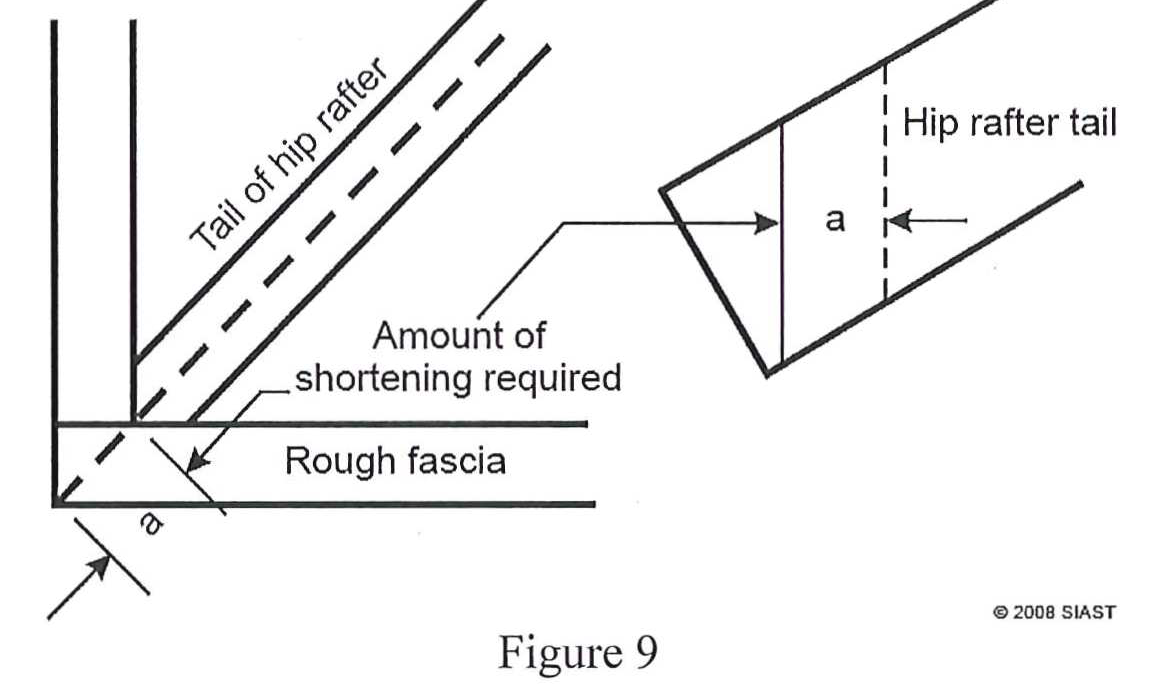
At the bottom of the hip rafter, we must deduct the full 45° thickness of the rough fascia (do not include the finish fascia).
Review Questions
- Explain how the theory length of the ridge on a hip roof is calculated.
- What is the theory length of the ridge for a hip roof on a building 28’-0” x 38’-0” with a 2’-0” overhang?
- What additions are made when finding the actual length of a ridge when using:
- Single cheek cut
- Double cheek cut
- Calculate the actual length of the ridge for the following buildings:
- Building A
- Building B
- What is the line length per unit of run for a hip rafter on a roof with a 5/12 slope?
- How many units of run are there in a roof on a building 26’-0” x 40’-0” for the following:
- The common rafter
- The hip rafter
- Calculate the following given the information below:
- Hip rafter length
- Hip rafter tail length
- What is “backing” a hip?
- How is a hip rafter dropped?
- How much is deducted at the rafter tail on a hip rafter with 2×6 rough fascia?
- Fill in the following table regarding hip rafters:
|
Slope |
Span |
Run |
Units of Run |
Unit of Rise |
Unit of Line Length |
Line length of Hip Rafter |
Overhang Projection |
Line Length of Overhang |
|
|
A |
1:4 |
30’-0” |
|
|
|
|
|
24” |
|
|
B |
1:2.4 |
24’-0” |
|
|
|
|
|
16” |
|
|
C |
1:3 |
26’-0” |
|
|
|
|
|
24” |
|
|
D |
1:2 |
30’-0” |
|
|
|
|
|
18” |
|
|
E |
1:1.71 |
28’-0” |
|
|
|
|
|
12” |
|
|
F |
1:5 |
24’-0” |
|
|
|
|
|
16” |
|
|
G |
1:4 |
22’-0” |
|
|
|
|
|
6” |
|
|
H |
1:3 |
18’-0” |
|
|
|
|
|
16” |
|
|
I |
1:2.4 |
21’-0” |
|
|
|
|
|
14” |
|
Answer:
- The building width is subtracted from the building length.
- 10’-0”
-
- Add ½ 45° thickness of the hip rafter and ½ 90° thickness of the ridge
- Add ½ 90° thickness of the common rafter
-
- 14’-3 5/8”
- 4’-1 ½”
- 17.69”
-
- 13
- 13
-
- 15’-11 13/16”
- 2’-10 7/8”
- Bevelling the top edge of the hip so that it is at the same angle and height as the jacks and commons
- By cutting the birdsmouth deeper so the top of the hip rafter lines up with the jacks and commons
- The full 45° thickness of the rough fascia (2 1/8”)
| Slope | Span | Run | Units of Run | Unit of Rise | Unit of Line Length | Line length of Hip Rafter | Overhang Projection | Line Length of Overhang | |
| A | 1:4 | 30’-0” | 15’-0” | 15 | 3 | 17.23” | 21’-6 7/16” | 24” | 2’-10 7/16” |
| B | 1:2.4 | 24’-0” | 12’-0” | 12 | 5 | 17.69” | 17’-8 5/16” | 16” | 1’-11 ½” |
| C | 1:3 | 26’-0” | 13’-0” | 13 | 4 | 17.44” | 18’-10 ¾” | 24” | 2’-10 7/8” |
| D | 1:2 | 30’-0” | 15’-0” | 15 | 6 | 18” | 22’-6” | 18” | 2’-3” |
| E | 1:1.71 | 28’-0” | 14’-0” | 14 | 7 | 18.36” | 21’-5 1/16” | 12” | 1’-6 3/8” |
| F | 1:5 | 24’-0” | 12’-0” | 12 | 8 | 18.76” | 18’-9 1/8” | 16” | 2’-0 15/16” |
| G | 1:4 | 22’-0” | 11’-0” | 11 | 3 | 17.23” | 15’-9 9/16” | 6” | 0’-8 5/8” |
| H | 1:3 | 18’-0” | 9’-0” | 9 | 4 | 17.44” | 13’-0 15/16” | 16” | 1’-11 3/16” |
| I | 1:2.4 | 21’-0” | 10’-6” | 10.5 | 5 | 17.69” | 15’-5 ¾” | 14” | 1’-8 5/8” |
