Topic 9 – Hip Jack Rafters

Hip jack rafters (also known simply as hip jacks) are simply common rafters that are shortened as they intersect the hip rafter. They rest on the exterior wall at 90° and are fastened to the side of the hip rafter. The geometry for hip jacks is very similar common rafters, with a few differences.

Run of Hip Jack Rafters

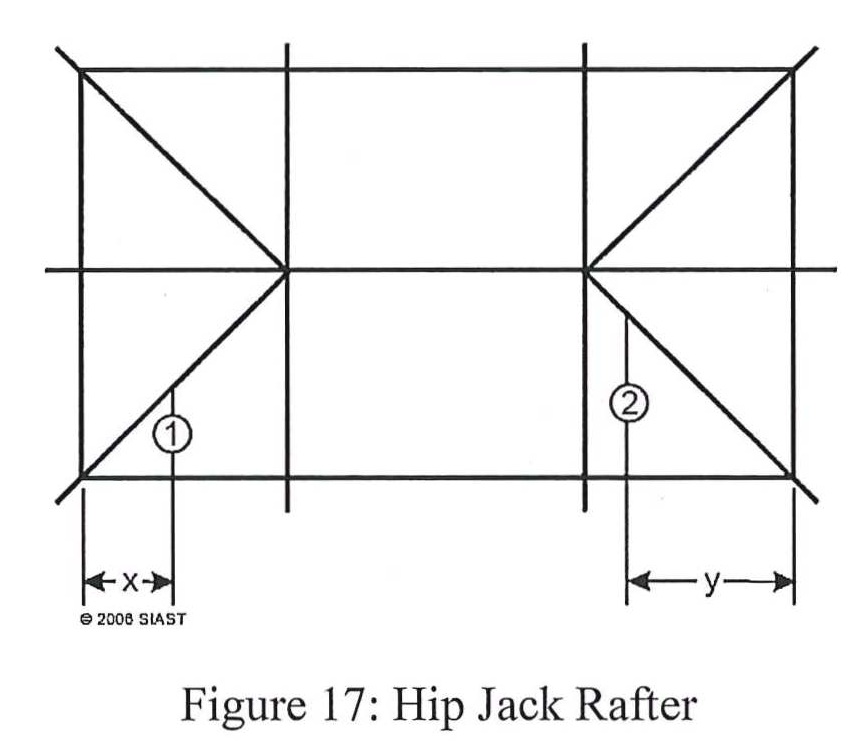
As they run 90° to the exterior wall, hip jacks have the same 12” unit run as common rafters. Their total run is measured from the exterior wall to the hip rafter and is equal to their distance from the corner of the building (not the corner of the roof). In figure 17 below, we can see two hip jacks labelled 1 and 2. The total run of hip jack 1 is equal to the distance marked x, and the total run of hip jack 2 is equal to the distance marked y:

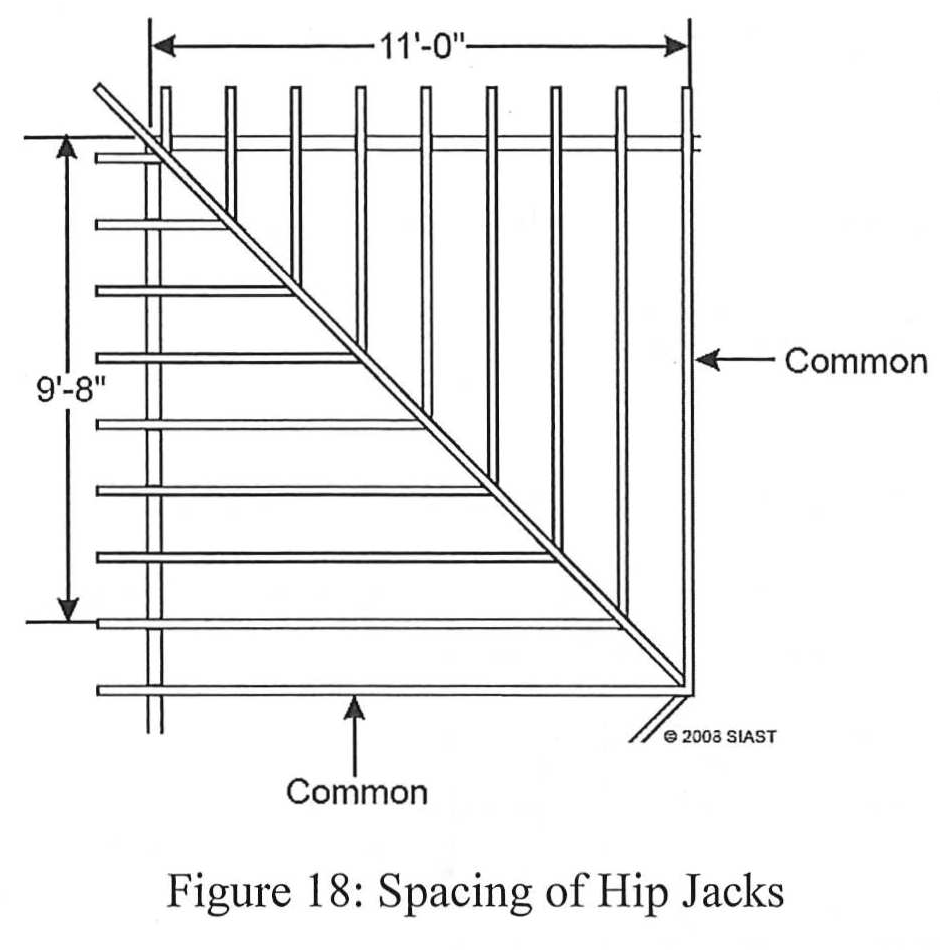The spacing of hip jacks begins at the common rafter that intersects the hip rafter and ridge. Because of this, the spacing works outwards from these points, and the shortest hip jack may or may not have equal spacing. We can use this knowledge to find the total run of hip jacks. In figure 18 (right), we see that the common rafters have a total run of 11’-0”. In this scenario, the rafters are spaced 16” O.C. The longest hip jack is therefore 16” closer to the corner than the common rafter, giving us a total run of 9’-8”.

Line Length of Hip Jacks

As hip jacks are essentially shortened common rafters, they share the same geometric properties as them. They share the same unit run (12”), unit rise, and therefore the same unit line length. Using the amount of units of run, which is the distance from the corner in decimal feet and multiplying it by the unit line length, we can calculate the line length of the hip jack.

For the building shown in figure 18, let’s assume a 4/12 slope (ULL = 12.65”) and find the line length of the longest hip jack (total run of 9’-8” or 9.67 units of run):

***Using the same building, can you calculate the line length of the second longest hip jack? (Use 16” centers)

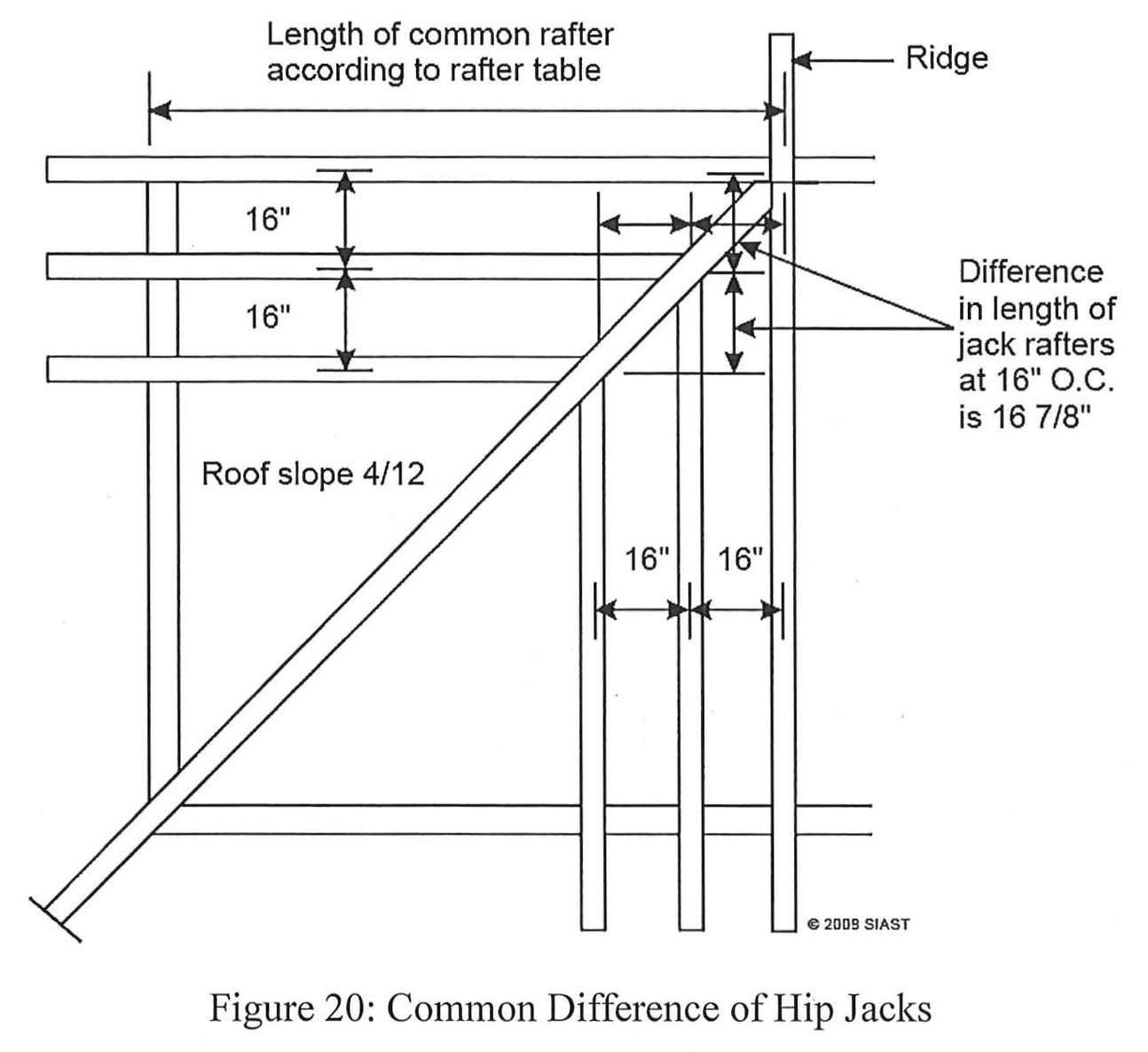
This method can be used to find the line lengths of all hip jacks; however, it may be beneficial to use the common difference to find each subsequent hip jack. The common difference is essentially how much shorter or longer each hip jack is to its neighbor. While these values can be found on framing squares with rafter tables, we can also calculate it using our spacing (in decimal feet) and our ULL. Using the same values (16 O.C. and 12.65” ULL), we can find the common difference between the hip jacks on the building in figure 18:

The rafter tails are calculated the same way as with common rafters.

Hip Jack Deductions

At the top of the hip jack, we must make deductions for the hip rafter. This deduction is equal to ½ the 45° thickness of the hip rafter. As it intersects with the hip rafter at an angle, there is a certain process which must be followed:

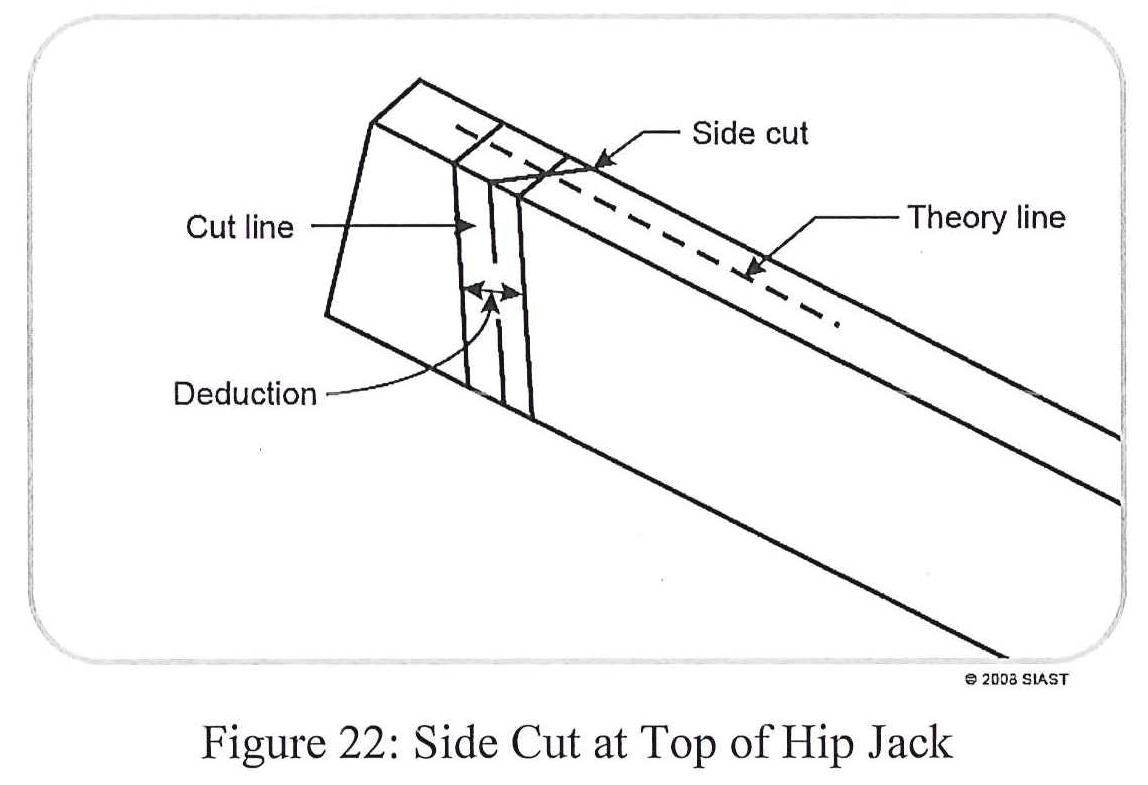
The measurements used for side cuts are not calculated but are instead found on the rafter tables on the framing square. It intersects the center of the board at the theory line after the deductions have been made and transferred to the edge and is the final step in locating the cut line for hip jacks.

Review Questions

1. The common difference in length of hip jacks for a 5/12 slope at 24” O.C. is _____ inches.
2. The common difference in length of hip jacks for a 3/12 slope at 16” on center is _____ inches.
3. How many units of run does a hip jack have if the jack is 4’-6” from the corner of the building?
4. What is the line length of a hip jack rafter that is 64” in from the corner of the building with a 4/12 slope?
5. Calculate the line length of the second longest hip jack in a hip roof with a 5/12 slope and rafters spaced at 16” O.C on a building 24’-0” x 30’-0”.
6. The hip jack is shortened at the top by deducting:

• All stock is 1 ½”

7. Calculate the theory lengths for the hip jacks below for the following hip roof:

• 28’-0” x 42’-0” building
• Roof slope 5/12
• Rafters 24” O.C.
• 2’-0” overhang

1. Line length of the longest hip jack
2. Line length of the shortest hip jack
3. Line length of the third longest hip jack

Answers:

1. 26”
2. 16 ½”
3. 4.5
4. 5’-7 7/16”
5. 10’-1 ¼”
6. ½ the 45° thickness of the hip rafter (1 1/16”)
7. 1. 13’-0”
   2. 2’-2”
   3. 8’-8”