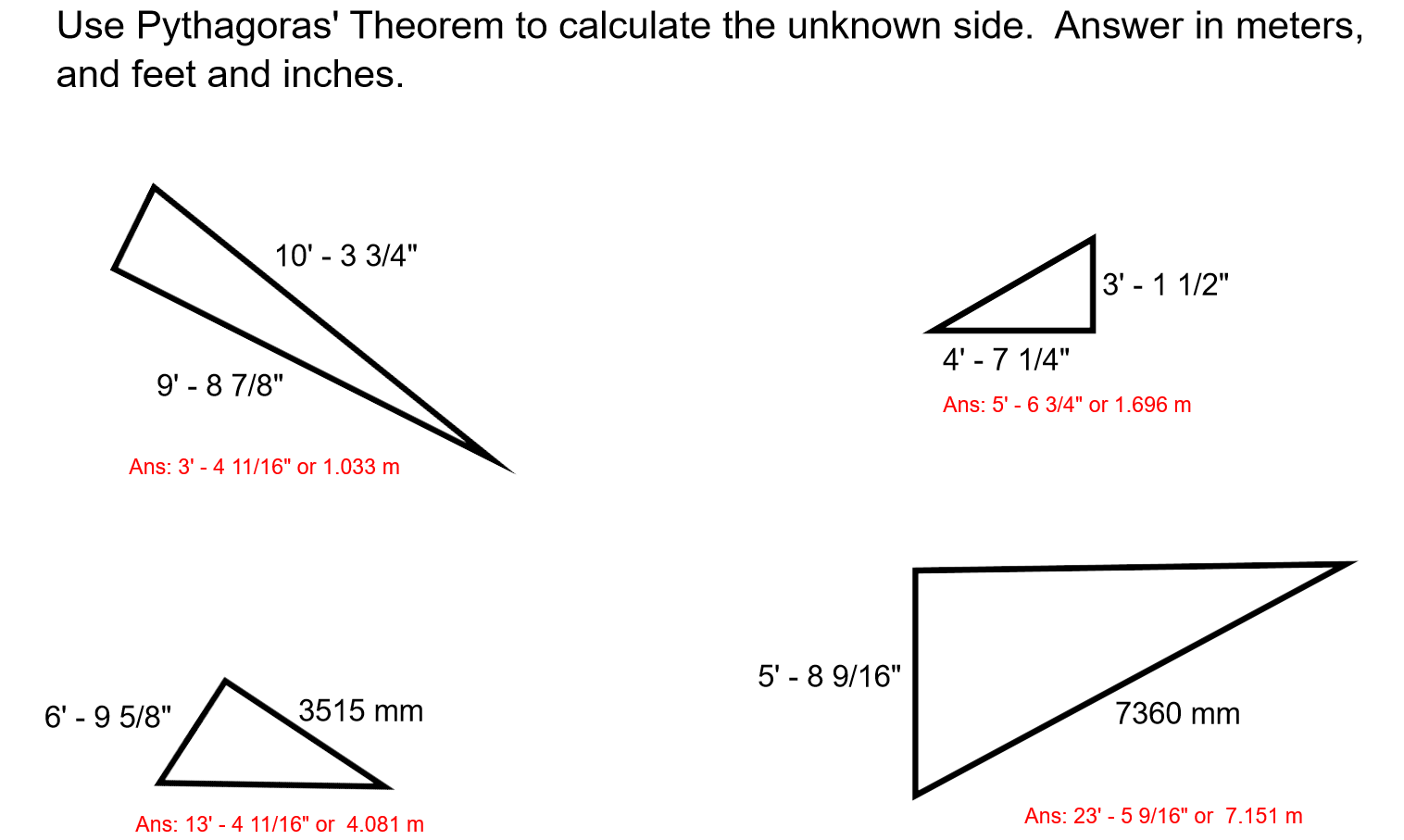
"

Math Checkup: Pythagoras’ Theorem

Another use for converting feet and inches to decimal feet and back is when using Pythagoras’ theorem to calculate a side length of a triangle.  If the sides of a triangle are measured in feet and inches, these need to be converted to decimal feet to use Pythagoras’ theorem.

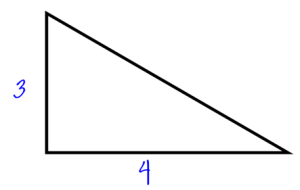
In a right angle triangle, the “legs” are labeled a or b, it doesn’t matter which.  The hypotenuse (longest side opposite the right angle.)

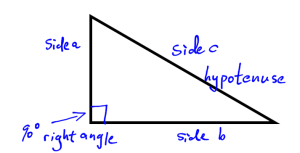
Pythagoras theorem has two forms.   image is used when finding the hypotenuse.  The other form,  image is used when finding the length of a side if you know the length of the hypotenuse.

Pythagoras’ Theorem Example

Calculate the length of the hypotenuse:

We need to find the length of side c, so we use the formula image.  To type this in the calculator, use the following keystrokes:

3 A picture containing textDescription automatically generated + 4 A picture containing textDescription automatically generated = IconDescription automatically generated with medium confidence

*Note:  the “equals” button is very important and often forgotten.

The answer is 5.  You can see that the famous 3 – 4 – 5 triangle comes from Pythagoras’ Theorem

Calculate the length of the side:

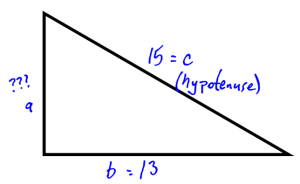
In this case, we know that the hypotenuse is 15.  Finding one side requires the formula image.

*Note: The hypotenuse (c) needs to be first or you will get a calculator error.

Use the following keystrokes:

15 A picture containing textDescription automatically generated – 13 A picture containing textDescription automatically generated = IconDescription automatically generated with medium confidence

The answer is 7.48.

Pythagoras’ Theorem with Feet and Inches

Calculate the hypotenuse length.

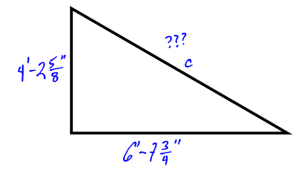
The first step is to calculate the feet and inch measurements to decimal feet.  We can use the  A picture containing text, plate, tableware, dishwareDescription automatically generated and image  buttons to store these values so we do not need to write anything down.

What I am calculating… What I am thinking…
2 + 5  8 =

12 =

+ 4 =

 Convert 4’ – 2 5/8” to decimal form.
A picture containing text, plate, tableware, dishwareDescription automatically generated image Store this value in the calculator so you don’t need to write down, and all the decimals are used.
7 + 3  4 =

12 =

+ 6 =

 Convert 6’ – 7 ¾” to decimal form.
A picture containing text, plate, tableware, dishwareDescription automatically generated image Optional: store this number in the second memory spot in your calculator
image 1 A picture containing textDescription automatically generated +  image 2  A picture containing textDescription automatically generated = IconDescription automatically generated with medium confidence
 		 Perform Pythagoras’ Theorem as in previous example.  The answer will be in decimal feet.  (8.7325…)
8’ – 8 13/16” Convert the answer in decimal feet to feet and inches.

Pythagoras’ Theorem Exercise Set 1

License

Icon for the Creative Commons Attribution 4.0 International License

Carpentry Refresher Program Manual Copyright © by Saskatchewan Indian Institute of Technologies-Trades and Industrial is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book