"

Topic 5– Use a Trigonometry in Building Layout

Inserting image...

Source: https://commons.wikimedia.org/wiki/File:Surveyor_s18.jpg

Trigonometry can be used to assist in building layout. Many locations can be laid out from a single point with blueprint information, a transit, and a few mathematical equations.

sine theta equals opposite over hypotenuse

cosine theta equals adjacent over hypotenuse

tangent theta equals opposite over adjacent

Curves and arcs can also be laid out using trigonometry and a transit or theodolite.

L e n g of t h o f C h of r o d equals D i a. m e t e r times open paren A n g of l e o f D e f of l e c t i o n times S I N close paren

A more common use of a transit is to determine the height of an object.

For more information refer to Instruction Sheet on Brightspace, CNST 204 (p. 61-73):

● IS 2.2 Trigonometric Functions for Building Layout

Review Questions

  1. What is the formula used to find the tangent of an angle?
  1. Solve the following
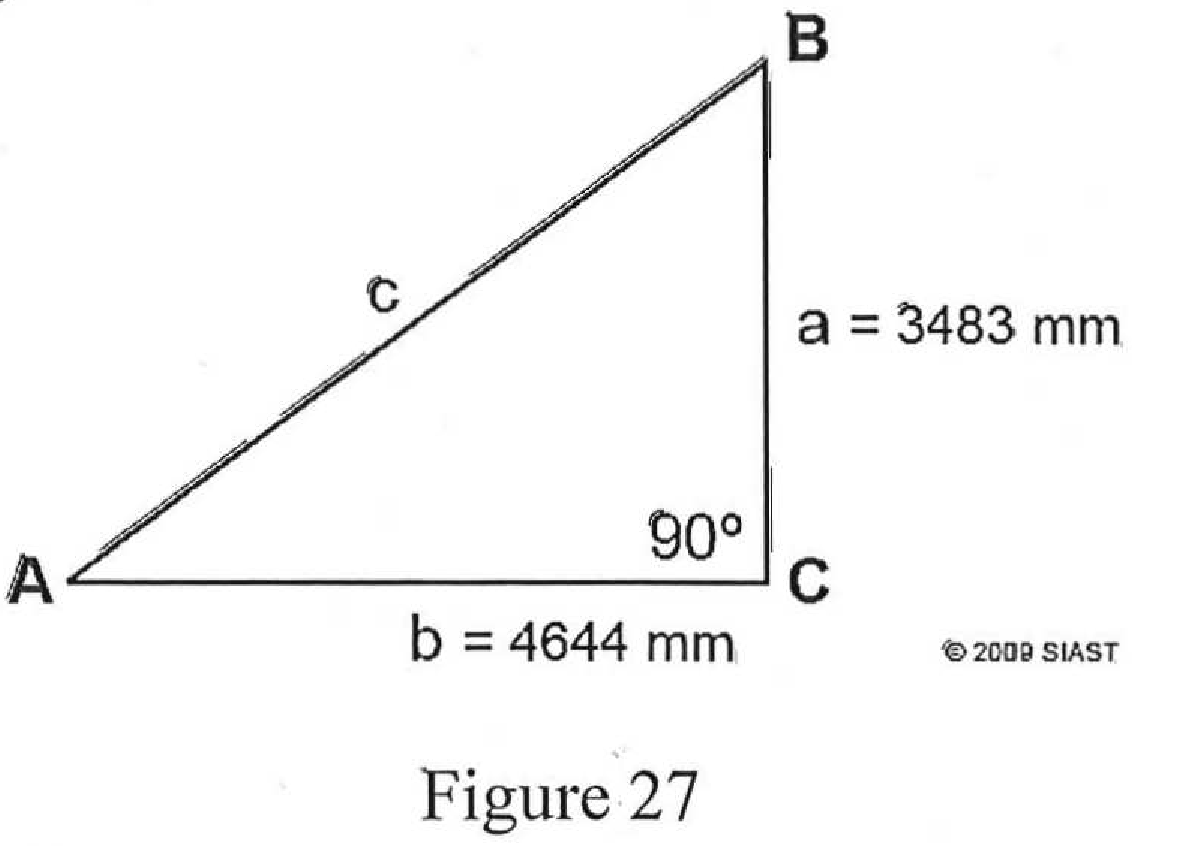
  1. In figure 27, calculate the angle of A:

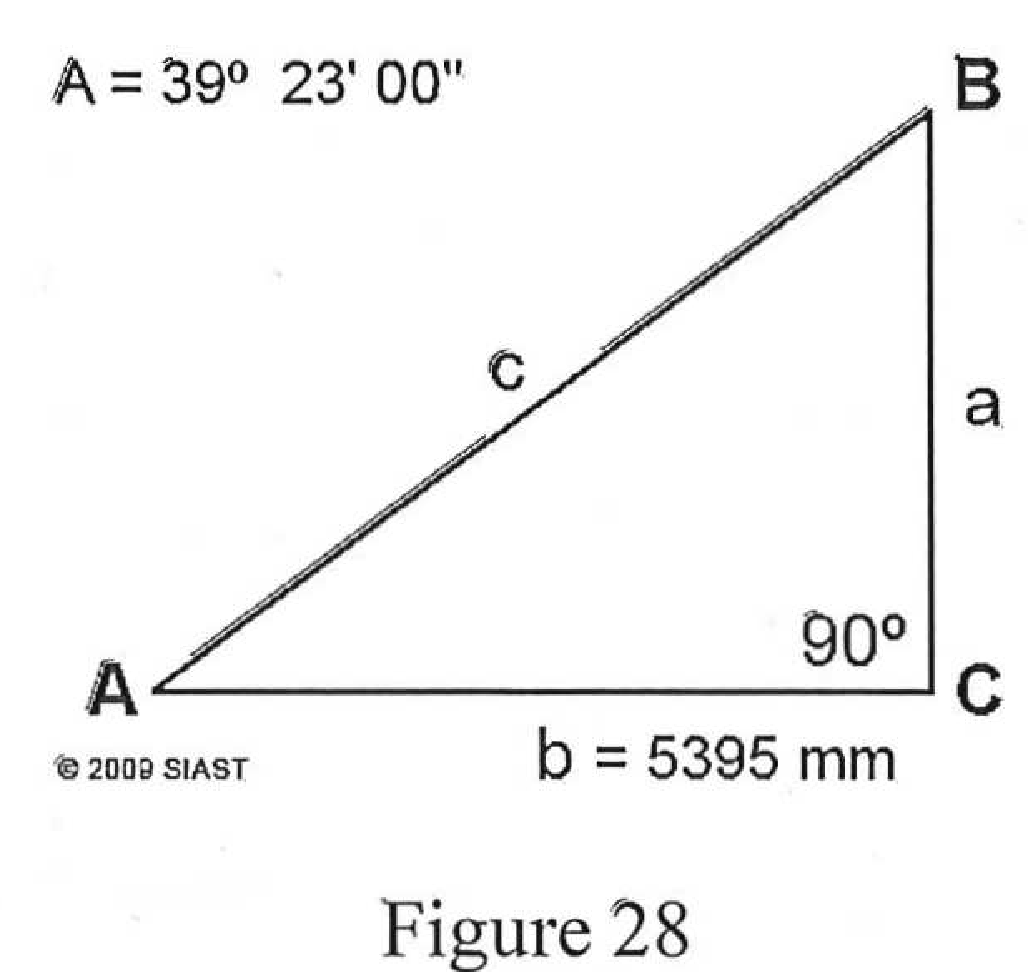
image

  1. In figure 28, calculate the length of side “a”.

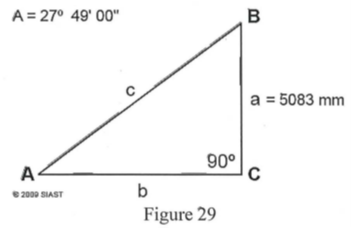
image

  1. In figure 29, calculate the length of side “b”

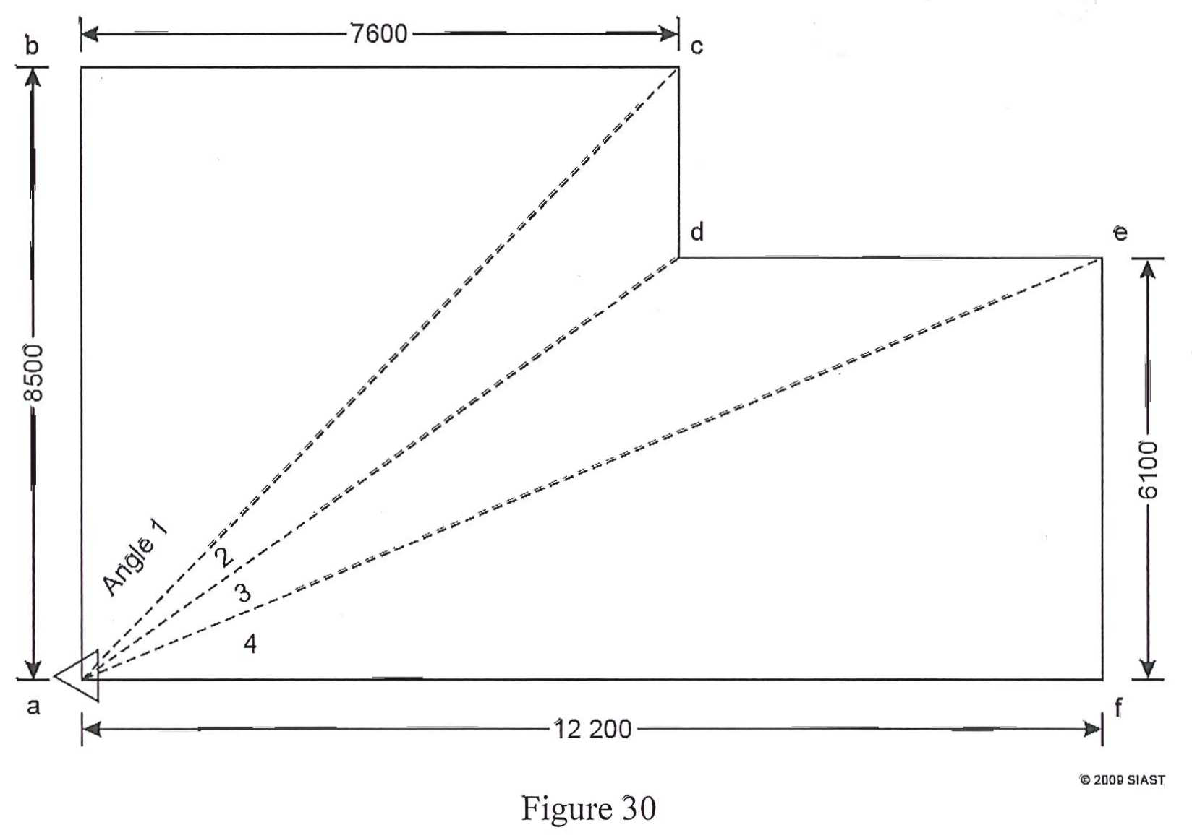
image

  1. Calculate the angle to be turned and the distances to be taped to lay out the building with the transit set up over point a only.:

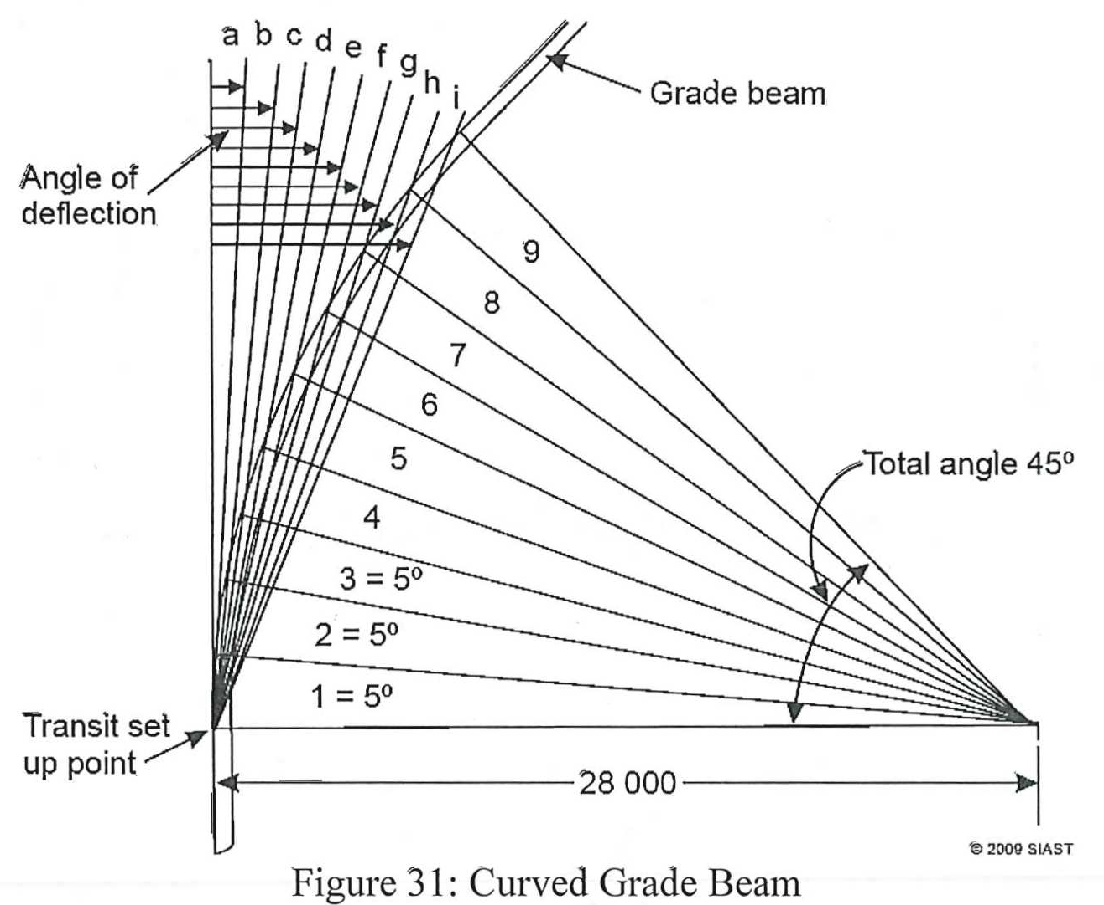
image

– Angle 1 is _____                     – Angle 3 is _____ 
– Distance ac is _____            – Distance ae is _____ 
– Angle 2 is _____                   – Angle 4 is _____ 
– Distance ad is _____        – Distance af is _____ 
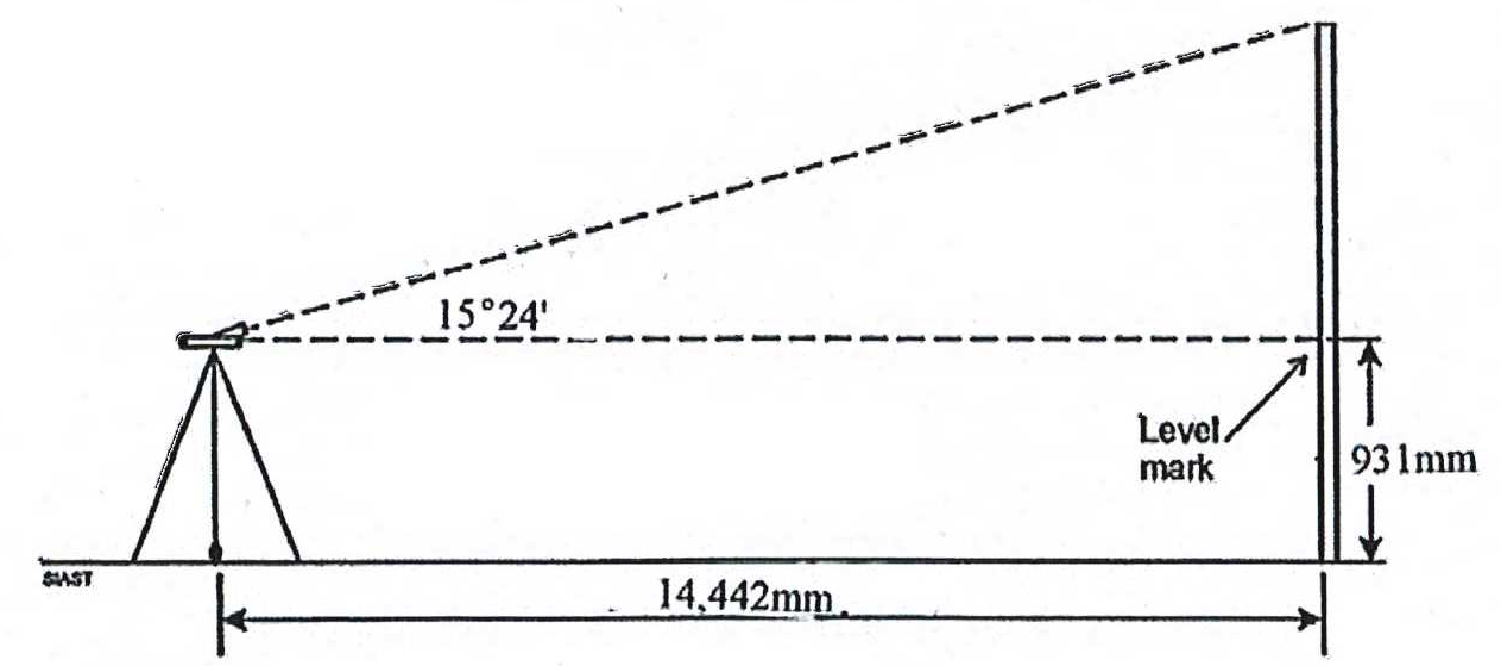
  1. Figure 31 shows a concrete grade beam with a curve in it. The total angle of the curve is 45°. The radius of the curve is 28 000 mm. Divide the curve into 9 parts and calculate the angles of deflection and the lengths of the chords so the curve can be laid out with a transit.image
a) Size of the first angle of deflection “a” _____ 
b) Length of chord for “a” _____ 
c) Size of second angle “b” _____ 
d) Length of chord for “b” _____ 
e) Size of third angle “c” _____ 
f) Length of chord for “c” _____
g) Size of fourth angle “d” _____ 
h) Length of chord for “d” _____ 
i) Size of fifth angle “e” _____
j) Length of chord for “e” _____ 
k) Size of sixth angle “f” _____ 
l) Length of chord for “f” _____ 
m) Size of seventh angle “g” _____ 
n) Length of chord for “g” _____ 
o) Size of eight angle “h” _____ 
p) Length of chord for “h” _____ 
q) Size of final angle “I” _____ 
r) Length of chord for “I” _____ 
  1. Calculate the height of the wall in the diagram below:

image

Answers:

  1. tangent theta equals opposite over adjacent
    1. Angle A is 36°52’12” 
    2. Side a is 4429 mm 
    3. Side b is 9634 mm 
    1. Angle 1 is _____ (41°48’)
    2. angle 3 is _____ (63°26’) 
    3. Distance ac is _____ (11402 mm)
    4. distance ae is _____ (13 640.01 mm) 
    5. Angle 2 is _____ (51° 15’)
    6.  angle 4 is _____ (90°)
    7. Distance ad is _____ (9745.25 mm)
    8. distance af is _____ (12 200 mm) 
    1. Angle 1 is (41°48’)
    2. angle 3 is (63°26’) 
    3. Distance ac is (11402 mm)
    4. distance ae is (13 640.01 mm) 
    5. Angle 2 is (51° 15’)
    6. angle 4 is (90°) 
    7. Distance ad is (9745.25 mm)
    8.  distance af is (12 200 mm) 
    9. Size of the first angle of deflection “a” (2°30’) 
    10. Length of chord for “e” _____ (12 121 mm) 
    11. Size of sixth angle “f” _____ (15°00’) 
    12. Length of chord for “f” _____ (14 494 mm) 
    13. Size of seventh angle “g” _____ (17°30’) 
    14. Length of chord for “g” _____ (16 840 mm) 
    15. Size of eight angle “h” _____ (20°00’) 
    16. Length of chord for “h” _____ (19 153 mm) 
    17. Size of final angle “I” _____ (22°30’) 
    18. Length of chord for “I” _____ (21 430 mm) 
  5. The height of the wall is 4909 mm.

License

Icon for the Creative Commons Attribution 4.0 International License

Carpentry Refresher Program Manual Copyright © by Saskatchewan Indian Institute of Technologies-Trades and Industrial is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book