Topic 2 – Gable Roof Components and Calculations
Parts of a Gable Roof
A typical gable roof consists of many components which can serve either structural or architectural purposes:
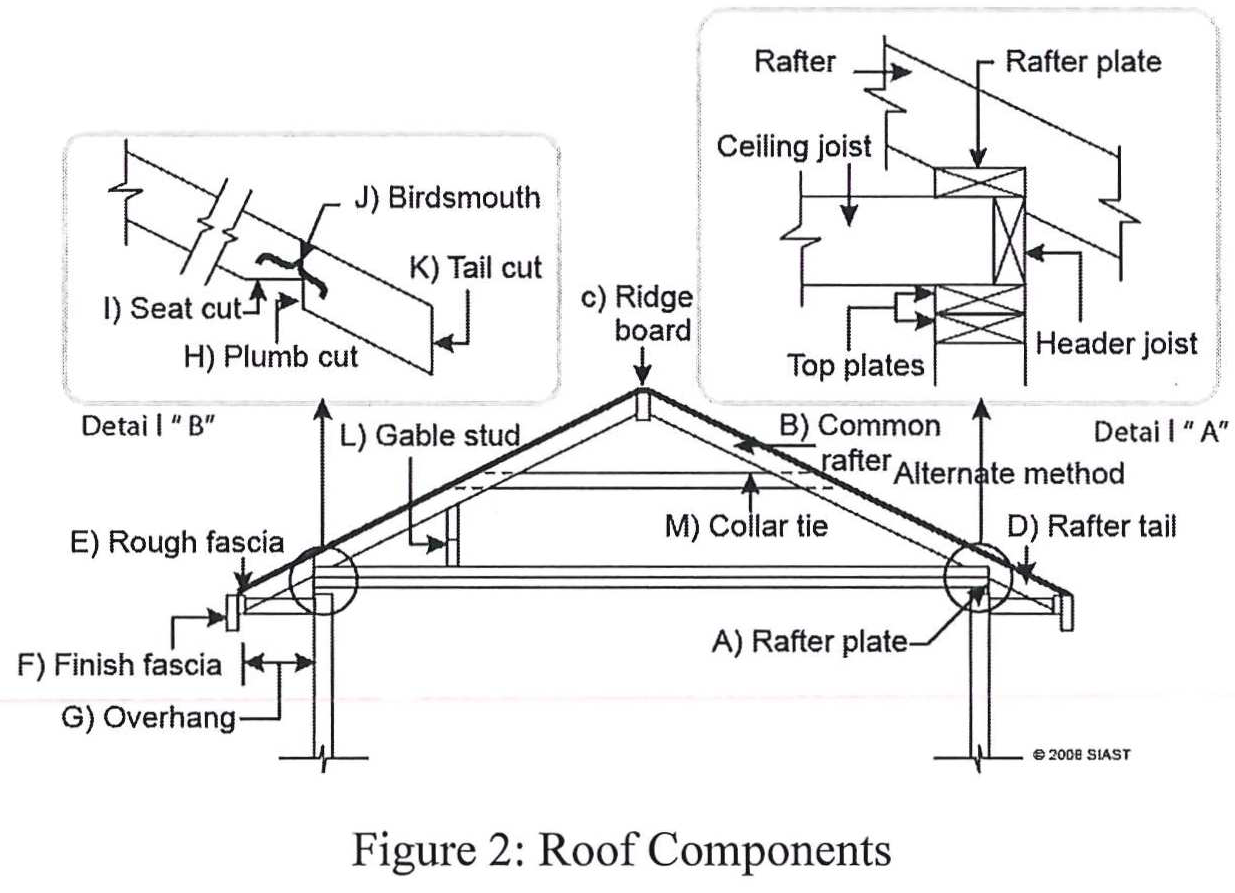
Familiarize yourself with these terms as they are used frequently when carrying out roof framing calculations.
Roof Slopes
The slope of a roof can be expressed in three different ways: in degrees, as a percentage, or as a ratio. The most common format roof slopes expressed in is using ratios between rise and run (rise/run). For imperial slopes, this rise to run ratio is expressed in inches, with the unit run always as 12”. The unit rise varies, which is how different slopes are achieved. The unit rise symbolizes how many inches a roof system will rise as it passes over 12” of horizontal distance. For example, a 4/12 roof will rise 4” for every foot (12”) it “runs”. The rise value is always written first.
The roof slope symbol is used on construction documents and can be found on the elevation drawings. It is usually situated above the roof line it is referencing:
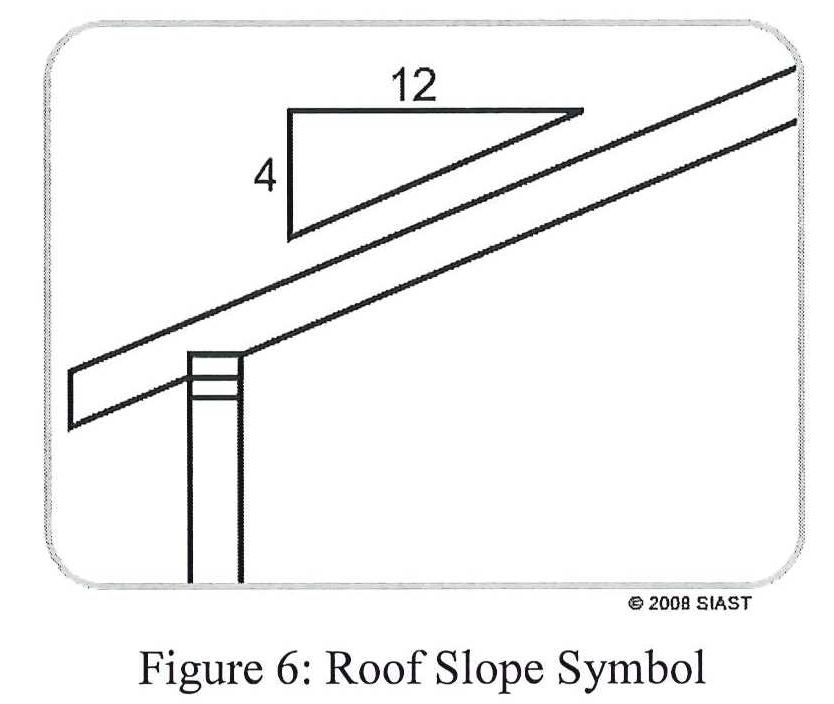
While it is necessary to use 12 as the unit of run when doing roof calculations, a roof slope may be expressed in a ratio that does not use 12 as the unit of run. In these cases, the unit triangle must be converted to over a unit run of 12. For example, the following triangle uses a slope ratio of 1:3.
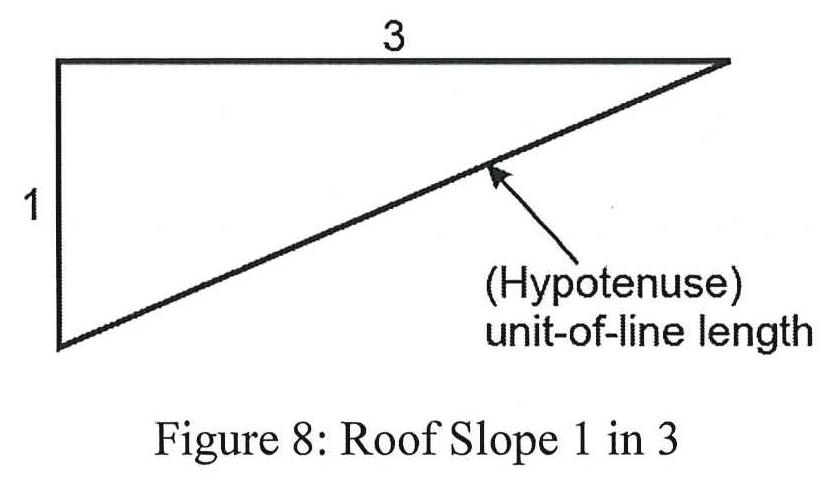
In order to use this slope ratio in our calculations, we must convert it to a slope over 12. We can find the ratio as follows:
When we rearrange this ratio, we can find that our unit rise is 4. This means that a roof slope of 1/3 is the same as a 4/12 slope; it is simply expressed in lower values.
***Find the slope ratio for a 1:2 and 1.33:1
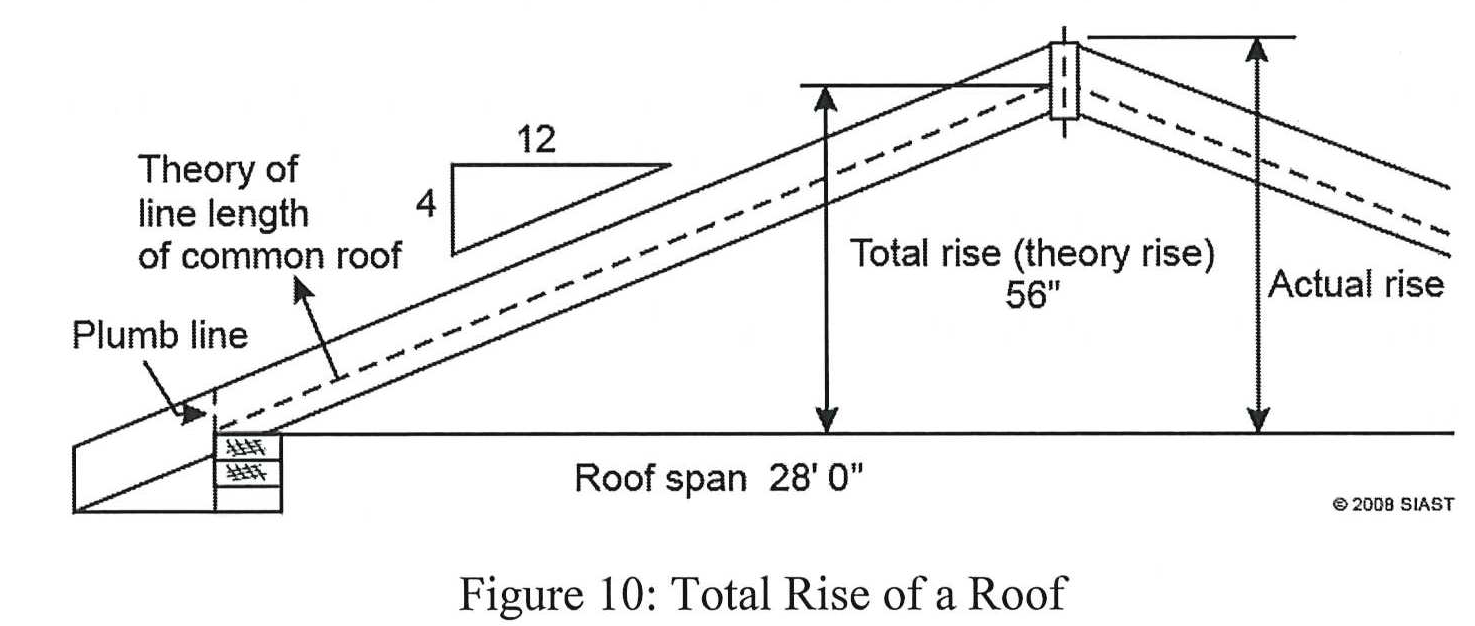
Total Run and Total Rise
There are three terms used to describe the geometry of the overall roof structure (see figure 9 and 10 below):
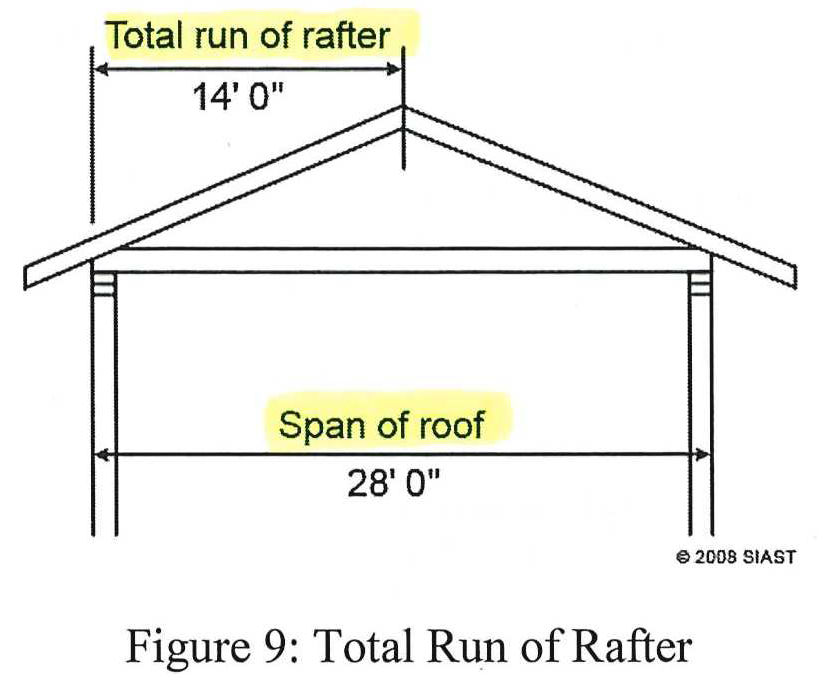
- Total Run = 24’ ÷ 2 = 12’ (12 units of run)
- Total Rise = 4” x 14 = 56”
The Roof Triangle
We can use the above measurements to find the line length of the common rafters. The line length is a measurement from the plumb cut at the birdsmouth to the center of the ridge. To find the line length, we will use the Pythagorean theorem a2 + b2 = c2, where a = total rise, b = total run, and c = line length of the common rafter:
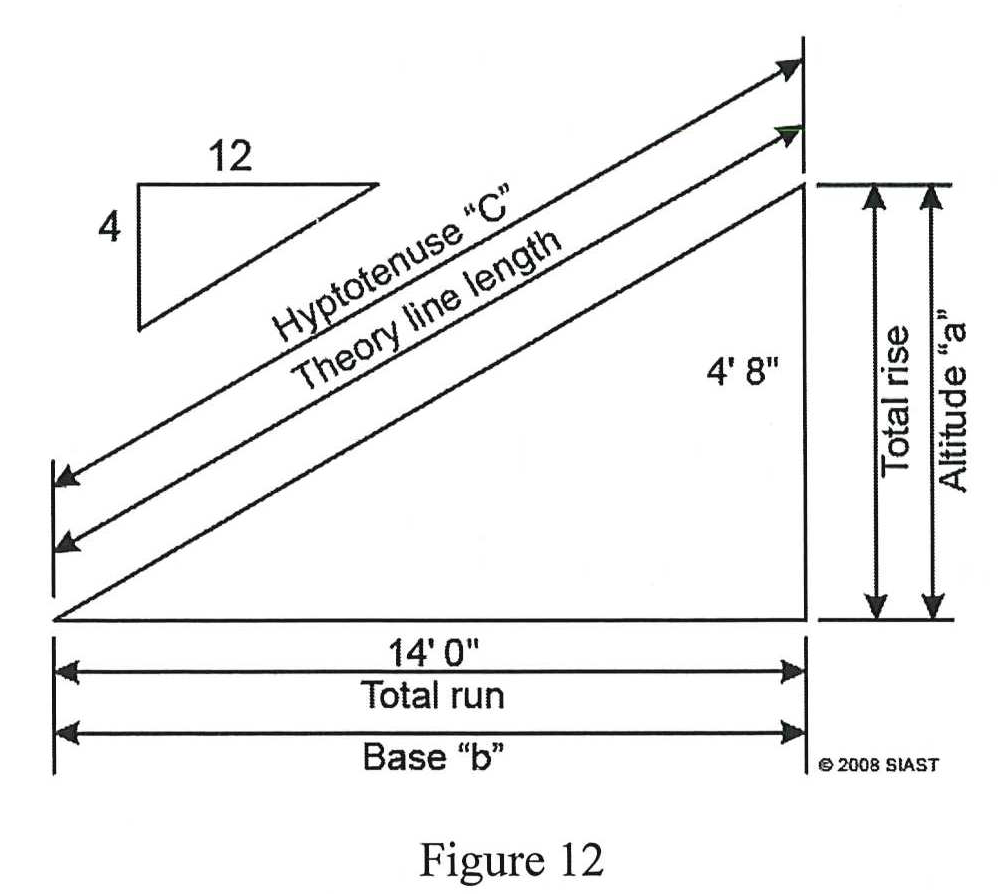
In order to use this equation, all of these values must be in the same units, and they must be in decimal form. We can use either decimal feet or decimal inches. We will find decimal feet and then input these values into the equation:
We will then need to convert this value in decimal feet to feet and inches:
This value of 14’-9 1/8” is the theory line length of the common rafters in this roof.
The Unit Triangle
A more common approach in finding the line lengths of common rafters is using the unit triangle. While again using the Pythagorean theorem, this is method find the unit line length (ULL), which is the hypotenuse of the unit (slope) triangle:
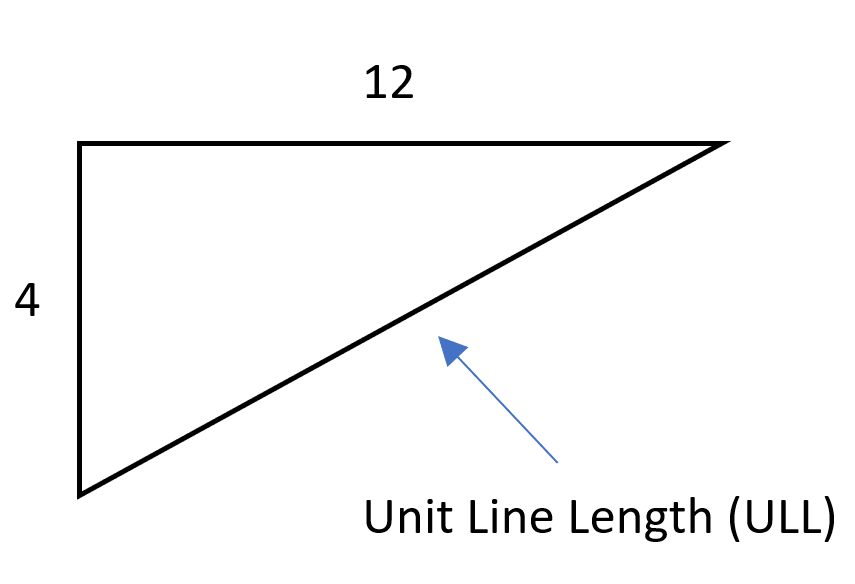
The unit line length for a 4/12 slope is therefore 12.65”. It is kept in decimal form to simplify calculations where it is used. This value can be used to calculate the line length of common rafters as well as other members of the roof system such as hip jacks (discussed in a later section). When using ULL to find the line length of common rafters, simply multiply the ULL (in inches) by the span of the rafter (units of run, in feet):
***Find the unit line length for the following slopes: 3/12 and 7/12
Rafter Tail
The line length of the rafter rail is calculated separately using the unit triangle. The total run of the rafter tail is equal to the overhang, expressed in decimal feet. For example, a 24” overhang is equal to 2’ or 2 units of run. Using the 12.65” ULL from a 4/12 slope, we can find the line length of the rafter tail:
***Find the length of a rafter tail for a 16” overhang and a 3/12 slope
Review Questions
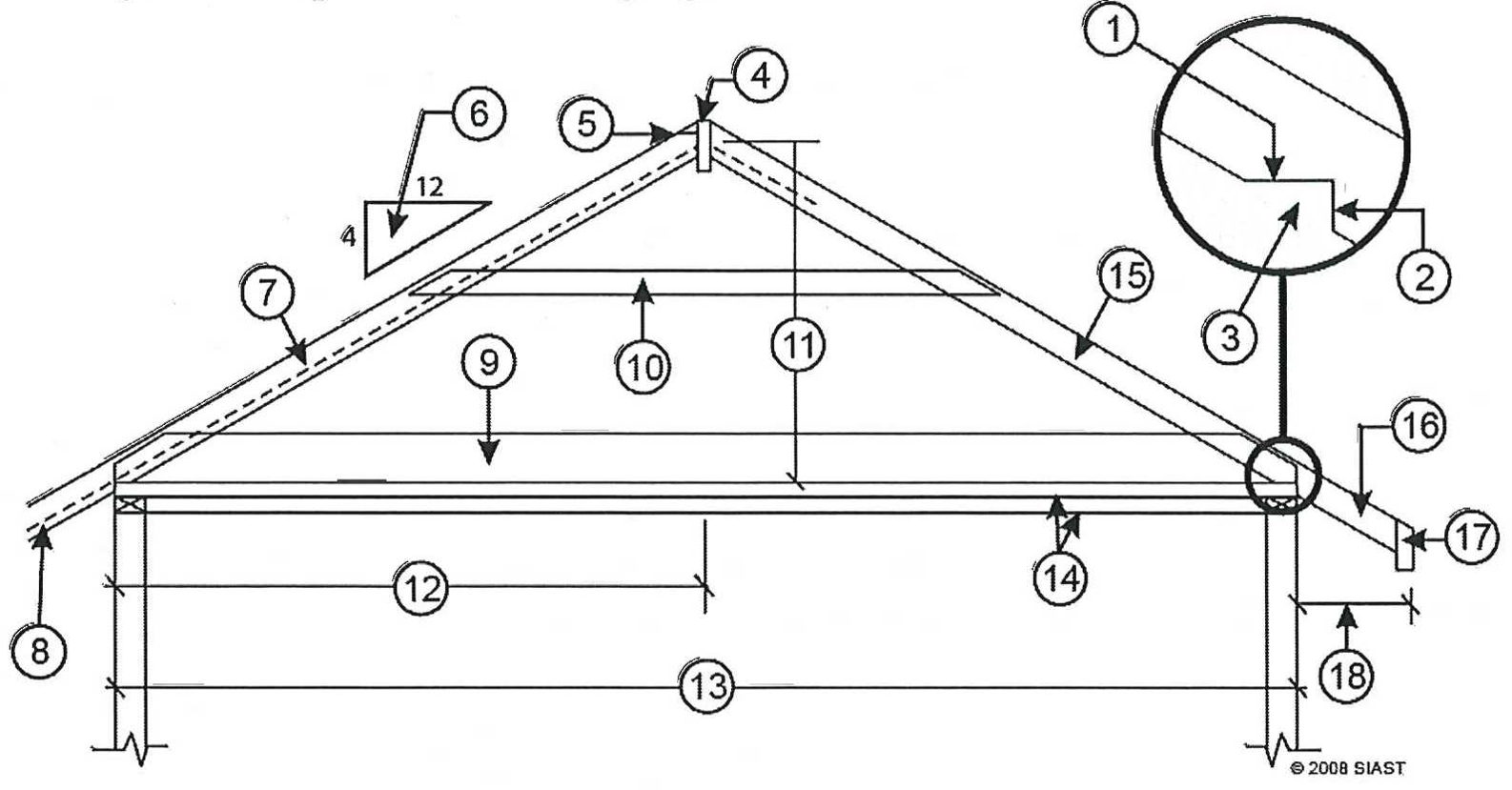
- Name the gable roof parts in the following figure:
- Convert the following roof slope ratios to rise per foot of run:
- 1:4
- 1:6
- 1:1
- 1:1.2
- 1.33:1
- What is the total rise for a roof with a rafter span of 12’ and a unit rise of 6”?
- What is the total rise for a roof with a roof span of 20’ and a unit rise of 8”?
- Calculate the line length of a common rafter for a building 22 feet wide and an 8/12 slope.
- What is the line length of a rafter tail for a 16” overhang using a 3/12 slope?
- Fill in the following table:
|
Slope Ratio |
Span of Roof |
Run of Rafter |
Number of Units of Run |
Unit of Rise |
Unit of Line Length |
Line Length of Rafter |
Overhang Projection |
Line Length of Overhang |
Total rise of Roof |
|
|
A |
1:3 |
32’-0” |
|
|
|
|
|
2’-0” |
|
|
|
B |
1:2.4 |
26’-0” |
|
|
|
|
|
1’-6” |
|
|
|
C |
1:1.71 |
24’-0” |
|
|
|
|
|
1’-0” |
|
|
|
D |
1:2 |
30’-0” |
|
|
|
|
|
2’-0” |
|
|
|
E |
1:4 |
28’-0” |
|
|
|
|
|
1’-4” |
|
|
|
F |
1:1.5 |
26’-0” |
|
|
|
|
|
1’-0” |
|
|
|
G |
1:3 |
24’-0” |
|
|
|
|
|
1’-4” |
|
|
|
H |
1:1.33 |
28’-0” |
|
|
|
|
|
1’-6” |
|
|
|
I |
1:2.4 |
30’-0” |
|
|
|
|
|
2’-0” |
|
|
Answer:
| 1 Seat cut | 10 Collar tie |
| 2 Plumb cut | 11 Total Rise |
| 3 Birdsmouth | 12 Run of roof or span of rafter |
| 4 Ridge board | 13 Span of roof |
| 5 Plumb cut at ridge | 14 Top plate and double top plate |
| 6 Roof Slope | 15 Common rafter |
| 7 Theory line length of rafter | 16 Rafter rail |
| 8 Theory line length of rafter tail | 17 Plumb cut at fascia |
| 9 Ceiling joist | 18 Overhang |
-
- 3/12
- 2/12
- 12/12
- 10/12
- 16/12
- 72” or 6’
- 80” or 6’-8”
- 158.64” or 13’-2 5/8”
- 16 ½”
| Slope Ratio | Span of Roof | Run of Rafter | Number of Units of Run | Unit of Rise | Unit of Line Length | Line Length of Rafter | Overhang Projection | Line Length of Overhang | Total rise of Roof | |
| A | 1:3 | 32’-0” | 16’-0” | 16 | 4 | 12.65” | 16’-10 3/8” | 2’-0” | 2’-1 5/16” | 5’-4” |
| B | 1:2.4 | 26’-0” | 13’-0” | 13 | 5 | 13” | 14’-1” | 1’-6” | 1’-7 ½” | 5’-5” |
| C | 1:1.71 | 24’-0” | 12’-0” | 12 | 7 | 13.89” | 13’-10 11/16” | 1’-0” | 1’-1 7/8” | 7’-0” |
| D | 1:2 | 30’-0” | 15’-0” | 15 | 6 | 13.42” | 16’-9 5/16” | 2’-0” | 2’-2 13/16” | 7’-6” |
| E | 1:4 | 28’-0” | 14’-0’ | 14 | 3 | 12.37” | 14’-5 3/16” | 1’-4” | 1’-4 7/16” | 3’-6” |
| F | 1:1.5 | 26’-0” | 13’-0” | 13 | 8 | 14.42” | 15’-7 7/16” | 1’-0” | 1’-2 7/16” | 8’-8” |
| G | 1:3 | 24’-0” | 12’-0” | 12 | 4 | 12.65” | 12’-7 13/16” | 1’-4” | 1’-4 13/16” | 4’-0” |
| H | 1:1.33 | 28’-0” | 14’-0” | 14 | 9 | 15” | 17’-6” | 1’-6” | 1’-10 ½” | 10’-6” |
| I | 1:2.4 | 30’-0” | 15’-0” | 15 | 5 | 13” | 16’-3” | 2’-0” | 2’-2” | 6’-3” |
