"

Topic 16 – Roofs with Unequal Slope

Gable Roof with Unequal Slopes

When given a gable roof with unequal slopes, the total rise needs to be calculated to find the total run of each side. We can use the ratio between the unit rise of each slope to find this relationship.

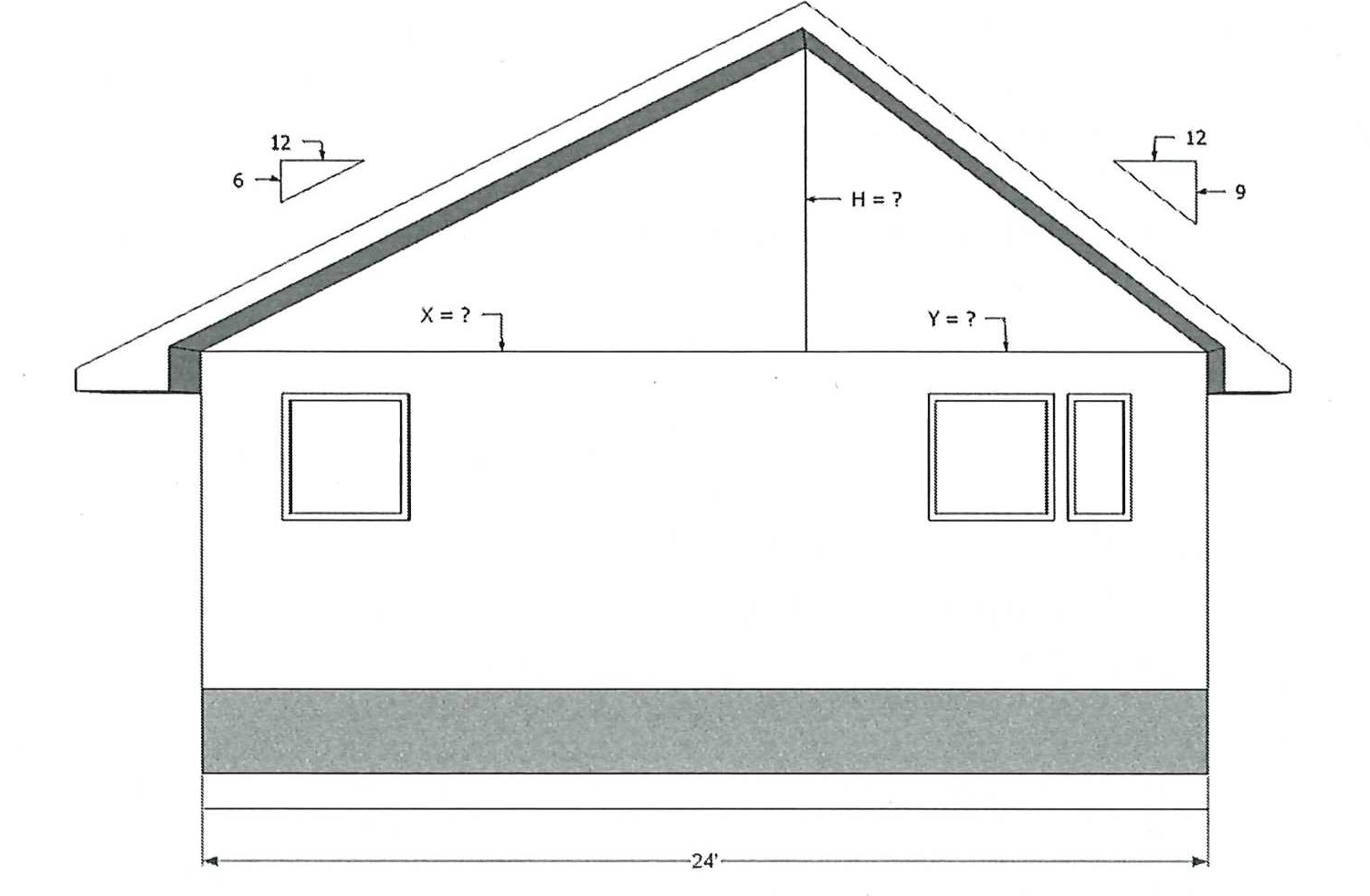
image

In the above image, we have a total rise of H, and a roof span of 24’-0”. The roof span is also equal to X plus Y, where X is greater than Y. To find how much larger X is, we will divide the larger unit rise by the smaller unit rise:

9 division sign 6 equals 1.5

 

This tells us that X is 1.5 times greater than Y, or, X = 1.5Y and can also be expressed in relation to the total span of the roof/width of the building:

24 raised to the prime power equals X plus Y equals 1.5 Y plus Y equals 2.5 Y

Y equals 24 feet divided by 2.5 equals 9.6 open paren u n i t s o f r u n close paren

Now that we have found the units of run for Y, we can simply subtract 9.6’ from 24’ to find the run of X and then multiply the units of run times the unit rise (for either side) to find the total rise H.

H equals 9.6 times 9 quotation mark equals the fraction with numerator 86.4 quotation mark and denominator 7 feet minus 23 over 8 right double quotation mark

For another example, we find the total rise of a roof over a 32’ x 46’ building with roof slopes of 5/12 and 8/12, where x is equal to the total run of the 5/12 side and y is equal to the total run on the 8/12 side.

x r i s e division sign y r i s e equals 8 divided by 5 equals 1.6 right arrow x equals 1.6 y

32 raised to the exponent prime end exponent equals 1.6 y plus y equals 2.6 y right arrow y equals 32 raised to the exponent prime end exponent division sign 2.6 equals 12.31 u n i t s o f r u n y

T o t a. l R i s e equals 12.31 times 8 equals 98.48 quotation mark o r 8 feet minus 2 and one half right double quotation mark

Unequal Slopes on Intersecting Roofs

In Topic 13.01.11, we were given an example of an intersecting roof which contained the same slope. Only when the roof spans were equal did their ridges meet at the top. In the example below, we have our ridges intersecting with different spans in the minor and major roofs. In order to accommodate this architectural design, the minor roof must have a steeper slope to reach the same elevation as the major roof.

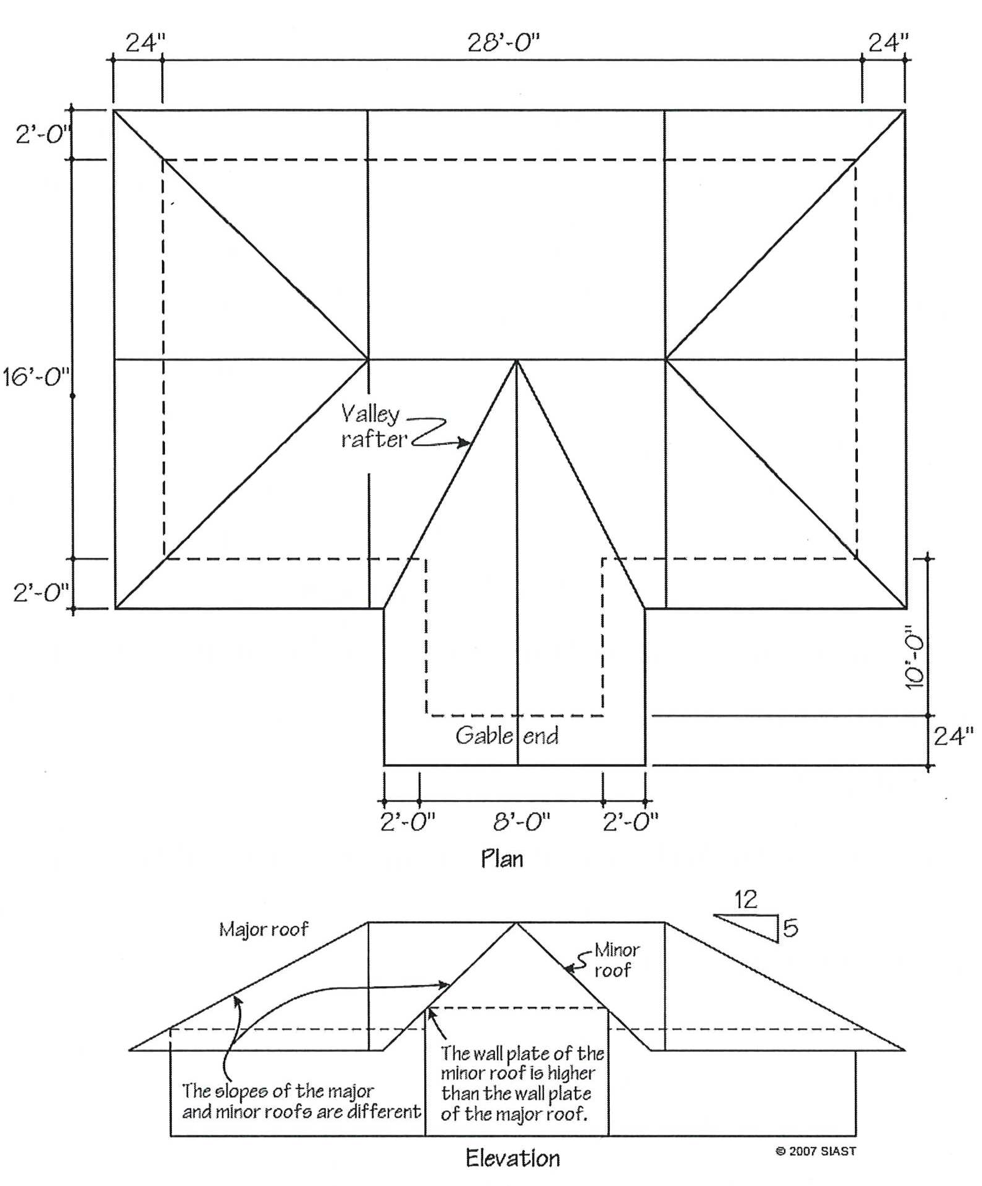
image

The primary obstacle when framing these roofs is maintaining a level, even overhang at the transition between the major and minor roofs. Since the minor roof must have a steeper slope, the rafter tail will also be steeper and therefore drop faster than the rafter tails of the major roof. In order to compensate for this, the walls on which the minor roof bears must be framed to a different height than the walls of the main structure.

As the structure is intended to be at the same elevation at the ridge and fascia, we can assume that the total rise from the fascia to the ridge will be the same for both the major and minor roofs. Since the rafter span, overhang, and slope of the major roof is known, we can calculate it as follows:

T o t a. l R i s e o f M a. j o r R o o f a. n d O v e r h of a. n g equals 10 times 5 quotation mark equals 50 quotation mark

With this, we can find the slope of the minor roof:

S l o p e M i n of o r r o o f equals the fraction with numerator T o t a. l R i s e open paren i n of c l u d i n of g r a. f of t e r t a. i l close paren and denominator T o t a. l R u n of open paren p l u s r a. f of t e r t a. i l close paren close paren right arrow x over 12 equals 50 over 72

x equals the fraction with numerator open paren 50 times 12 close paren and denominator 72 equals 8.33

S l o p e M i n o r R o o f equals 8.33 over 12

With knowing both the slope of the major and minor roofs, we can find the total rise of each overhang and then find the difference, which will tell us how much higher the walls must be framed under the minor roof:

T o t a. l R i s e 5 over 12 O v e r h of a. n g equals 5 times 2 equals 10 quotation mark

T o t a. l R i s e 8.33 over 12 O v e r h of a. n g equals 8.33 times 2 equals 16.67 quotation mark

D i f of f of e r e n c e i n O v e r h of a. n g H of e i g of h of t equals 16.67 quotation mark negative 10 quotation mark equals 6.67 quotation mark open paren 6 11 over 16 right double quotation mark close paren

The above results tell us the walls under the minor roof must be framed 6 11/16” higher than the walls under the major roof to maintain an even, level fascia.

We can also compress the above into a single equation, where x is equal to the total rise of the minor roof overhang:

the fraction with numerator t o t a. l r i s e o f m a. i n r o o f i n c l u d i n g o v e r h of a. n g and denominator t o t a. l r u n o f M i n o r r o o f i n c l u d i n g o v e r h of a. n g equals the fraction with numerator x and denominator t o t a. l r u n o f o v e r h of a. n g

the fraction with numerator 50 quotation mark and denominator 72 prime prime equals x over 24 quotation mark right arrow x equals the fraction with numerator 50 times 24 and denominator 72 equals 16.67 quotation mark o r 16 11 over 16 right double quotation mark

We can then, as the process above, find the difference it the rise of each overhang to find the difference in wall height:

D i f of f of e r e n c e i n w a. l l h of e i g of h of t equals 16 11 over 16 right double quotation mark negative 10 right double quotation mark equals 6 11 over 16 right double quotation mark

Review Questions

  1. Find the total rise of a building 22’ x 40’ with a gable roof with slopes of 6/12 and 10/12.
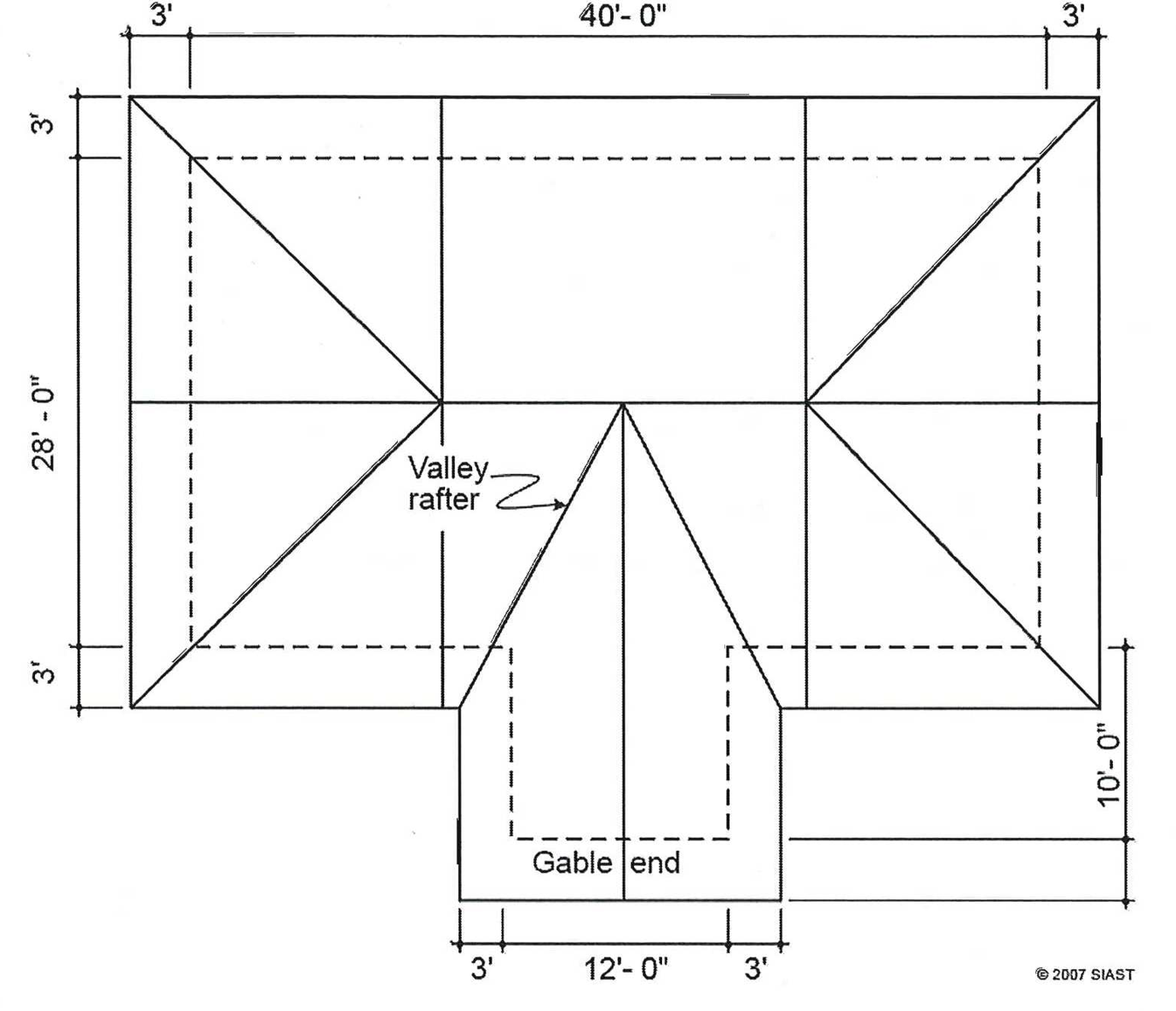
  2. Using the figure below, find how much higher the walls underneath the minor roof will have to be framed to produce an even, level fascia. The slope on the major roof is 4/12. To help in the process, find the following:

image

 Answers:

  1. 6’-10 ½”
  2. The wall under the minor roof must be framed 10 11/16” higher under the minor roof.

License

Icon for the Creative Commons Attribution 4.0 International License

Carpentry Refresher Program Manual Copyright © by Saskatchewan Indian Institute of Technologies-Trades and Industrial is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book