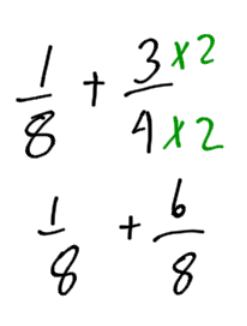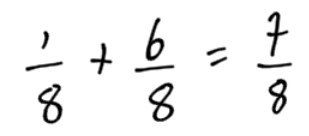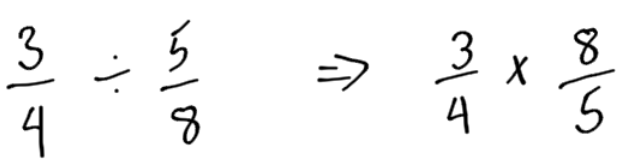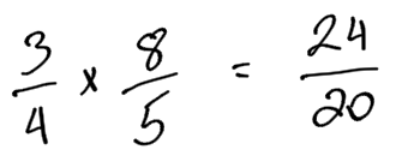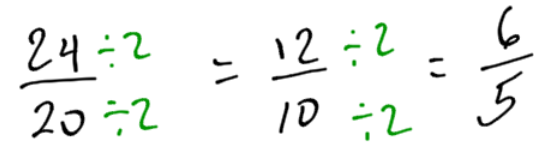2 Fractions, Decimals and Percentages
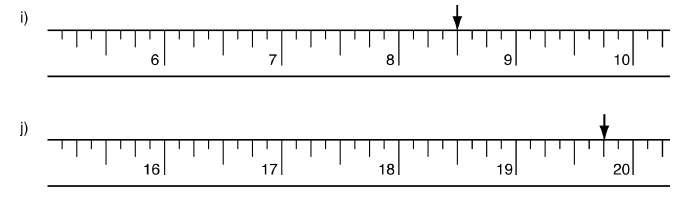
Section Information
Outcome/Competency: You will be able to solve problems using mathematical operations on fractions and decimals; and percentage.
Timing: 25h
Rationale: Why is it important for you to learn this skill?
Most things in life are not whole: minutes are fractions of hours, sixteenths are fractions of inches, pieces of pizza are fractions of the whole pizza, tax is a fraction of your income. Fractions, decimals, and percentages represent quantities that aren’t whole. It is essential, for example, to know how to use fractions when measuring in inches; and measuring in inches is something every tradesperson needs to know.
Objectives:
To be competent in this area, the individual must be able to:
- Simplify (reduce) and expand to create equivalent fractions.
- Employ the correct mathematical operation to answer a question given a scenario.
- Convert between percentages, ratios, fractions, and decimals
- Describe the relationship between fractions and division
Learning Goals
- Use a tape measurer to read, identify and convert measurements and fractions
- Solve problems with fractions, decimals, and percentages by hand
- Model and solve situational problems using extended functionality on the calculator
Introduction:
This module addresses how to solve problems using mathematical operations on fractions and decimals, and percentage. To understand this, we will look at an imperial tape measure (feet and inches) so we can also review measuring. You will complete practice exercises throughout and by the end of this outcome, you will realize that fractions and decimals and percentage are all related.
Chapter Contents:
- Topic 1: The Imperial Tape Measure
- Topic 2: Reading the Imperial Tape Measure
- 2.1 Using the Imperial Steel Tape
- Topic 3: Equivalent Fractions
- Topic 4: Mixed Numbers
- Topic 5: Adding and Subtracting Fractions
- Topic 6: Multiplying and Dividing Fractions
- Topic 7: Fractions, Decimals, and Percent
- Test: Outcome 2
Topic 1: The Imperial Tape Measure
The imperial tape measure (standard tape measure) measures length in feet, inches, and fractions of an inch. This tape measure can be confusing because all the markings in between inches have different “units.”
On this tape measure, there are only markings for full inches:

The problem is, this tape measure would not be good at measuring small things shorter than one inch. We need a smaller unit. Let’s divide the tape measure in half. This tape measure has a marking for each half inch.
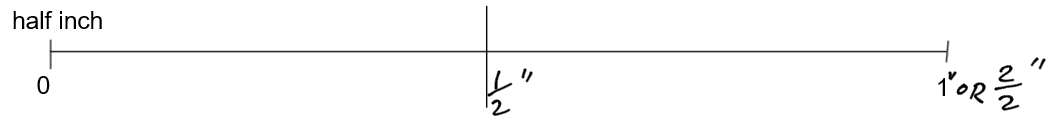
The problem is, still, that we may measure things that are smaller than half an inch. We need to divide the tape measure into even smaller units. If we divide each half inch in half, we will have four markings. These markings are called “quarters.” Notice how is in the same position as
. Notice also how
is the same as 1 inch. We will come back to that later.
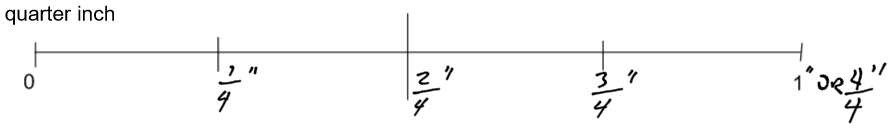
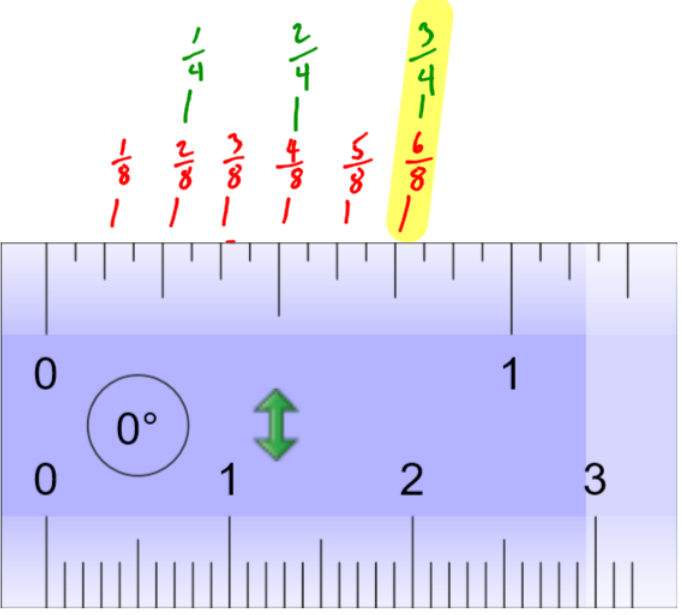
In order to measure smaller and small things, we create smaller and smaller units, or subdivisions, on the ruler. There are “eighths” where the inch is divided into eight, and “sixteenths” where the inch is divided into sixteen. Generally, the smallest unit we work with is a sixteenth of an inch, although some rulers are divided into thirty-seconds of an inch.
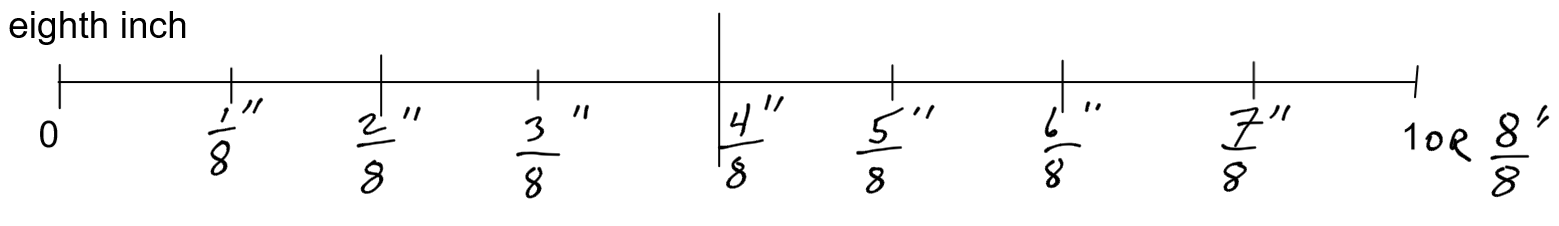
Note that is in the same place as
,
is in the same place as
, and
is in the same place as
.

Practice Exercises
Practice Labeling the Ruler
Using the rulers shown above, write down the measurements that are the same.
|
Sixteenths |
Eighths |
Quarters |
Halves |
Whole Inches |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Practice Labeling the Ruler Solutions:
|
Sixteenths |
Eighths |
Quarters |
Halves |
Whole Inches |
|
|
|
|
|
|
|
|
1/8 |
|
|
|
|
|
|
|
|
|
|
|
2/8 |
1/4 |
|
|
|
|
|
|
|
|
|
|
3/8 |
|
|
|
|
|
|
|
|
|
|
|
4/8 |
2/4 |
1/2 |
|
|
|
|
|
|
|
|
|
5/8 |
|
|
|
|
|
|
|
|
|
|
|
6/8 |
3/4 |
|
|
|
|
|
|
|
|
|
|
7/8 |
|
|
|
|
|
|
|
|
|
|
|
8/8 |
4/4 |
2/21 |
1 |
Ordering Measurements from Small to Large
[h5p id=”50″]
Topic 2: Reading the Imperial Tape Measure
Workers use rulers or other measuring devices frequently in their trade. Most of the numbers that you will use in your work will come from measurements.
The scale of each measuring device determines the precision of the measurement. The more precise the measurement has to be, the smaller the scale divisions needed.
Historically, the steel tape measure was used to measure various lengths of steel in inches and fractional parts of an inch or in millimetres (or centimetres). In this learning step, you will practice performing linear measurements with an Imperial and metric steel tapes.
2.1 Use Imperial Steel Tape
 This Photo by Unknown Author is licensed under CC BY-SA
This Photo by Unknown Author is licensed under CC BY-SA
You must make yourself familiar with the fractional parts of inches and their equivalencies on the steel tape. Steel tapes are often graduated in 1/16 inches, but can be graduated in 1/4-inch, 1/8 inch, or 1/32 inch.
The Imperial steel tape is calibrated in fractional inches. The number of inches and feet is indicated.
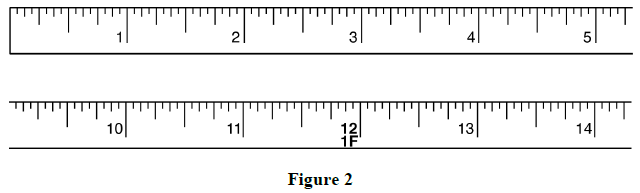
The following diagram of an enlarged steel tape shows the fractional inch measurements and their equivalencies for a steel tape graduated in1/8 inch.
Notice that the lines for whole inches are the longest. The next longest lines are the 1/2 inch lines, then 1/4 inch lines, etc.
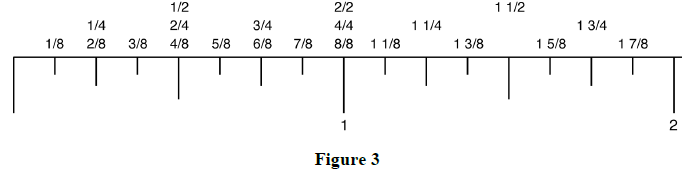
The following enlarged steel tape shows only the reduced fractional inch measurements for a steel tape graduated in 1/16 inch.
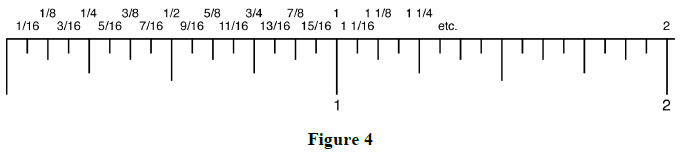
Again, the lines for whole inches are the longest, the next longest lines are the 1/2-inch lines, and so on. The 1/16-inch lines are the shortest.
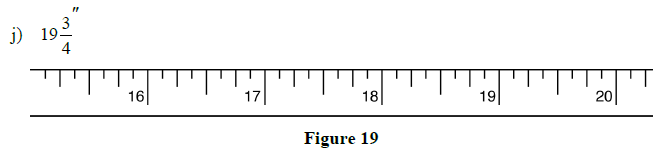
Example 1
Mark off a length of inches

You need to identify how this steel tape is graduated (1/8, 1/16, 1/32 )
One way is to count the number of spaces between zero and 1 inch.
Another way is to use the size of the lines: the longest is 1/2, the next 1/4, then 1/8, then 1/16.
This steel tape is graduated in 1/16 inch.
This means 1/8 that inch marks are the second shortest lines and larger (because 1/4 = 2/8, etc.)
Move to 3 inches, count 5/8 inch after that, and mark.

Answer

Example 2
State the measure of the mark below:

This steel tape is graduated in 1/16 inch.
The longest lines are 1/2, and the next longest (where the mark is) are 1/4.
From 11 inches, count the 1/4 inch lines and larger (because 1/2 = 2/4)
This line is 11 3/4 inches.
Example 3
State the measure of the line below

This steel tape is graduated in 1/8 inch.
The line to be measured ends at the smallest graduated line, at a 1/8 mark.
Count the number of 1/8 inch marks past 24 inches. Remember that 1/4 = 2/8.
This line is inches.
2.1 Review Exercises: Using the Steel Tape Measure
1. Mark the indicated lengths on the steel tapes below:
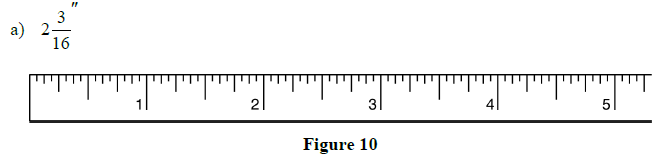
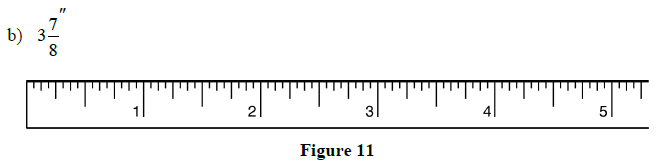
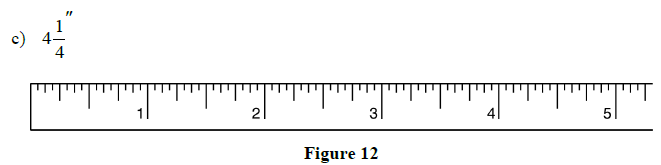
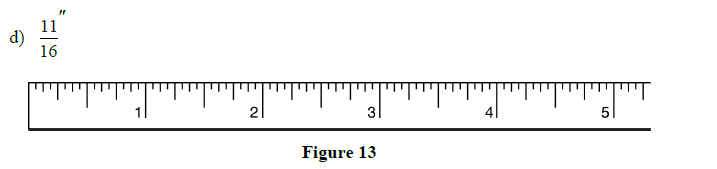
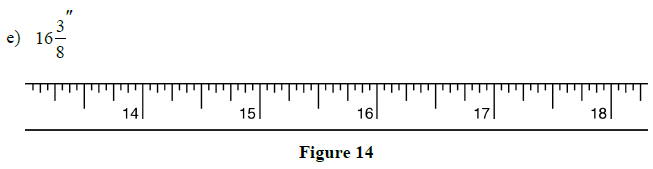
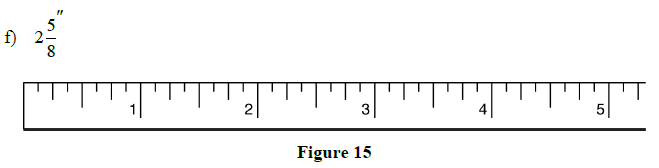
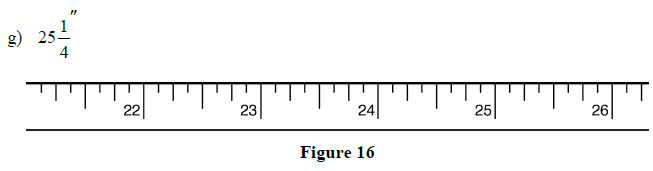
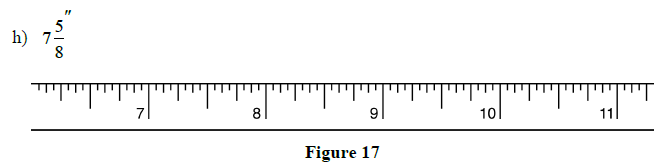
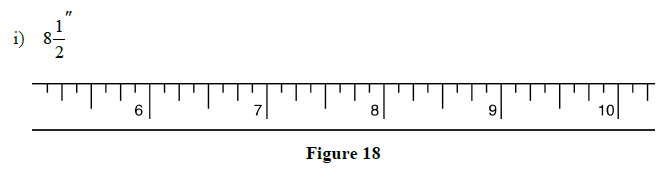
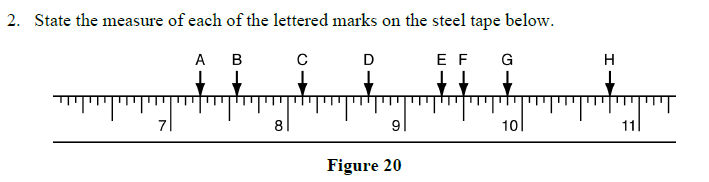
a)
b)
c)
d)
e)
f)
g)
h)
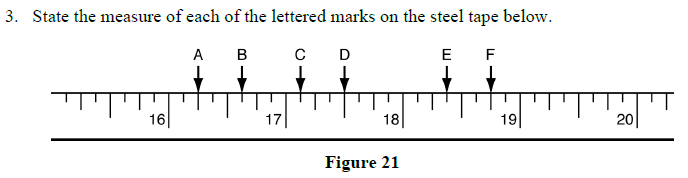
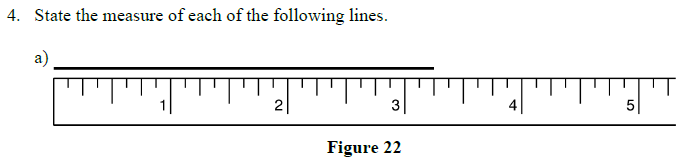



2.1 Review Exercises Solutions:
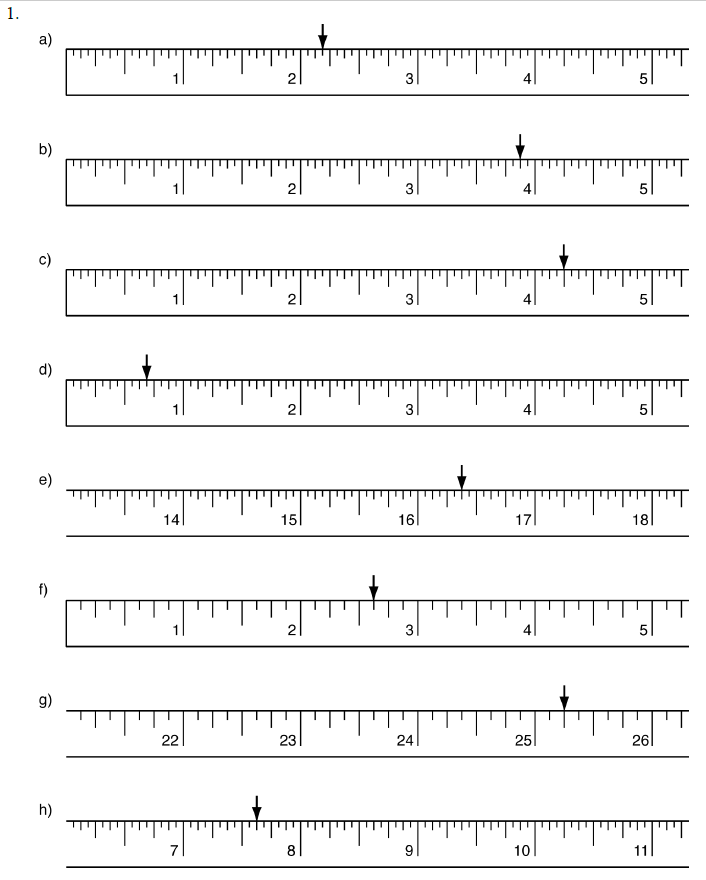
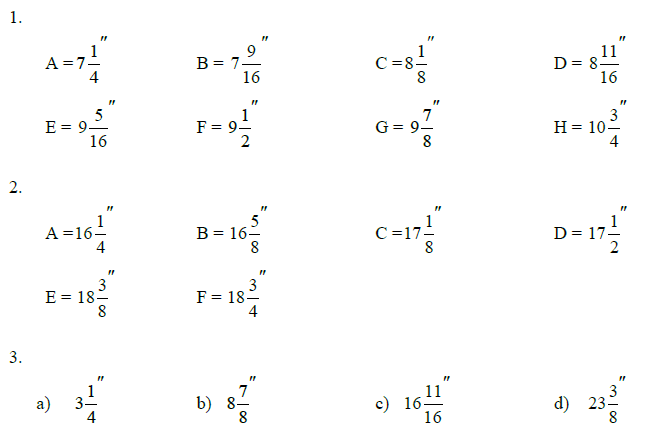
Topic 3: Equivalent Fractions
In the previous exercise (practice labeling the ruler) we noticed that is the same is
, for example. Or
is the same is
is the same as . These fractions all happen at the same place on the ruler, but they are labelled differently. These are called equivalent fractions.
3.1 Reducing Fractions
Changing from to
is called reducing (or simplifying.) We are reducing the numbers to make them smaller. There is a way to do this with math, so you don’t need to look at the ruler to see which are the same. If you divide the top number by two, that gives you the new top number: one. If you divide the bottom number by two, that gives you the new bottom number: eight.
To reduce a fraction, divide both the top number and the bottom number by the same number.
Knowing how to reduce fractions is necessary because when reading a tape measure, you always say the fraction in reduced form. For example, you read to
.
Example 1
Reduce the fraction .
By looking at the ruler, we can see the answer is .
We can also divide the top number by 2, and the bottom number by 2, so we don’t need to look at a ruler.
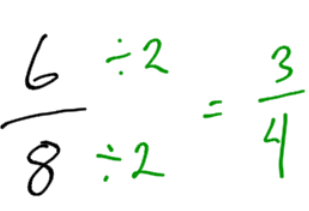
NOTE: with tape measurement fractions, if the top number is even, you can always reduce by dividing by 2.
NOTE: In some cases, you may be able to divide by 4, or 8, but if you start with 2 and repeat, you will always end up with the same answer.
Divide by two twice:
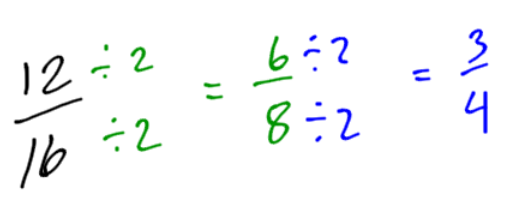
Divide by four also gives the same answer.
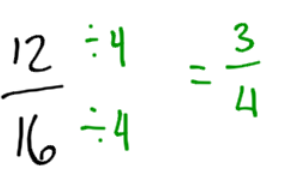
3.1 Practice Exercises: Reducing Fractions.
Write the following fractions in reduced form using math.
3.1 Practice Exercise Solutions:
3.2 Expanding Fractions
Expanding fractions is the opposite of reducing fractions. The top and bottom number get larger. We can do this by multiplying the top and bottom by the same number. We will see that expanding fractions is sometimes necessary when adding two fractions together.
Example 2
Expand the fraction into eighths. The means, write the fraction over eight instead of two.
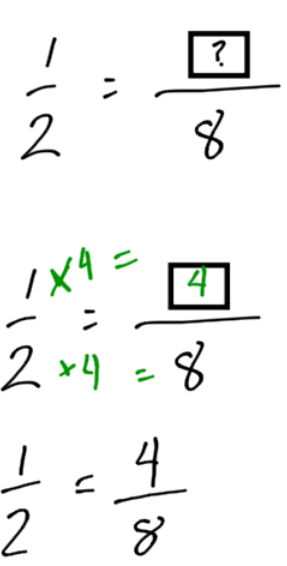
To expand a fraction, multiply both the top number and the bottom number by the same number.
3.2 Practice Exercises: Expanding Fractions
Expand the following fractions to have the correct bottom number.
into 16th’s
into 128th’s
into 16th’s
into 32nd’s
into 32nd’s
3.2 Practice Exercise Solutions:
Topic 4: Mixed Numbers
When counting on a tape measure, you can start counting at zero, in fractions, and ignore the whole inch numbers. In this example, we are going to measure the red line:
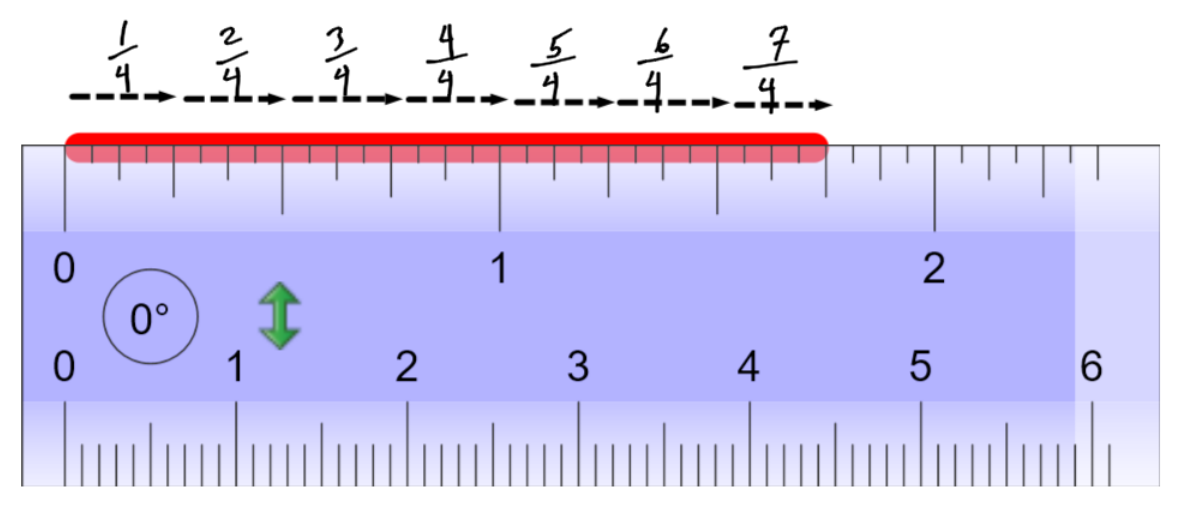
The red line is inches long. On the other hand, we know the red line is at least one inch long, and a little bit more:
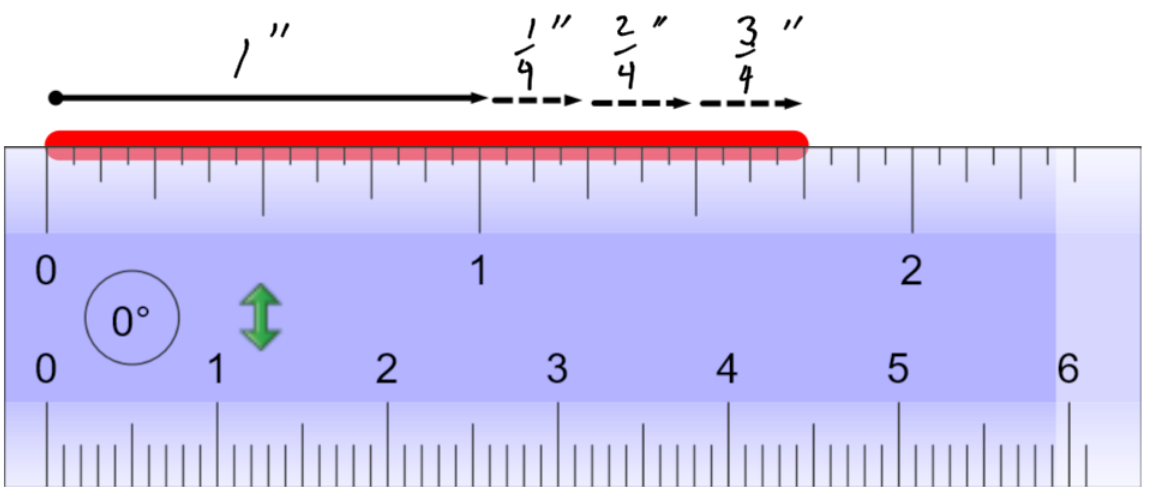
We can say the line is 1 inch plus inches long. Simply, the line is
inches long.
is an improper fraction. The top number is larger than the bottom. It represents a length that is longer than one inch.
is a mixed number. The whole number of inches are split out and written separately. When giving tape measure measurements, you always use mixed numbers. When multiplying or dividing fractions by hand, you need to use improper fractions.
4.1 Changing Improper Fractions to Mixed Numbers
Example 1
Write the fraction as a mixed number.
is an improper fraction. We can tell because the top number is larger than the bottom. On the ruler,
” looks like this:
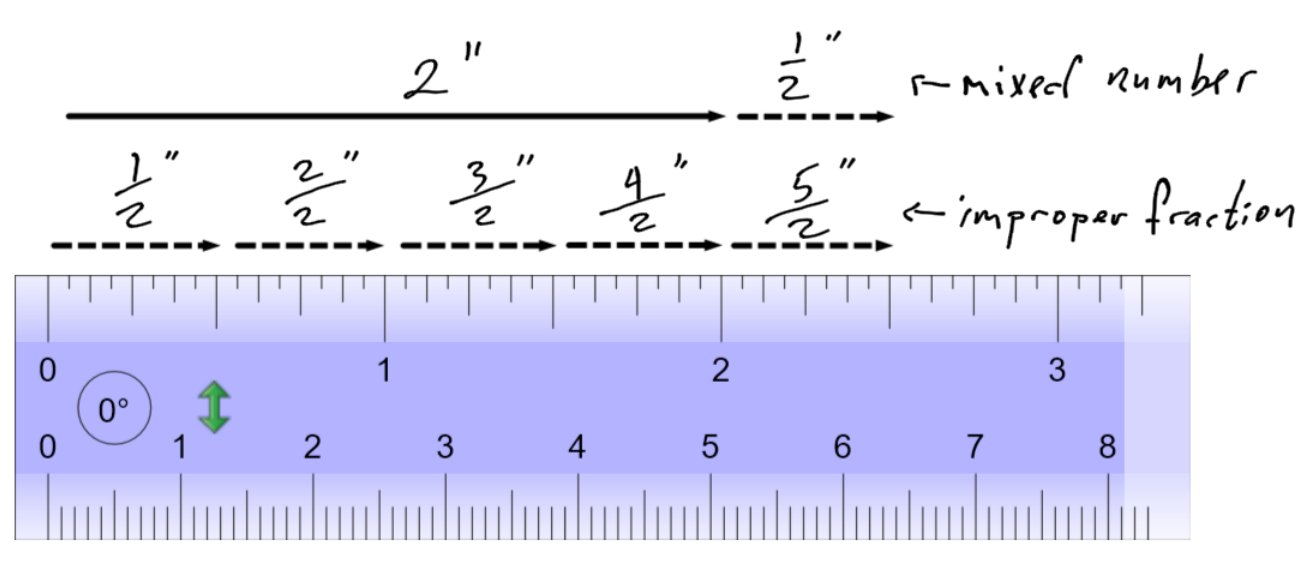
We can see that ” is the same measurement as
”.
Example 2
Write the fraction as a mixed number using math.
There is a way to change improper fractions to mixed numbers by using math instead of looking at your ruler.
What you need to ask yourself is: “how many groups of two can fit into five?” It helps to draw a picture:
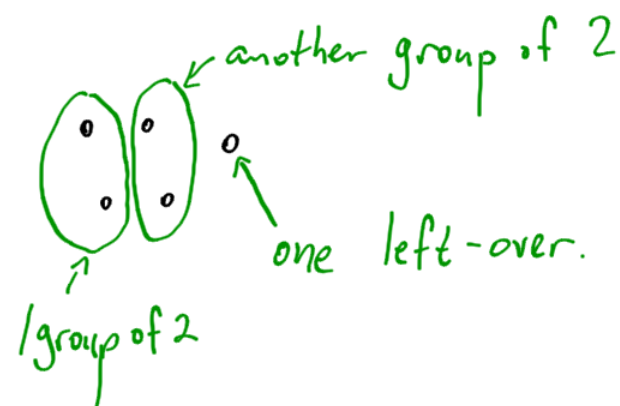
What we are essentially doing is long division:
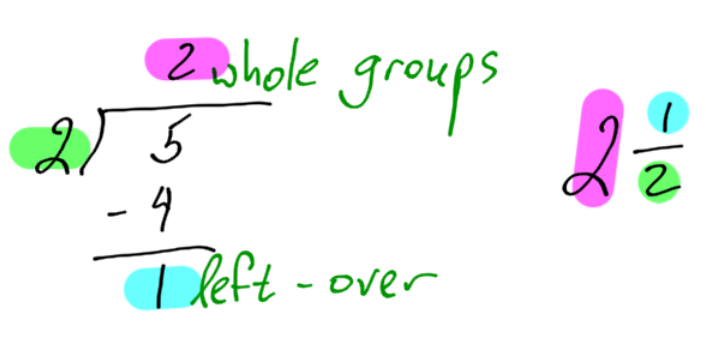
To change an improper fraction to a mixed number, use long division. The answer is the whole number. The left-over is the top number of the fraction.
4.2 Changing Mixed Numbers to Improper Fractions
Example 3
Write the mixed number as an improper fraction.
If we start at the beginning of the ruler and start counting in quarters, ” is the same as
”.
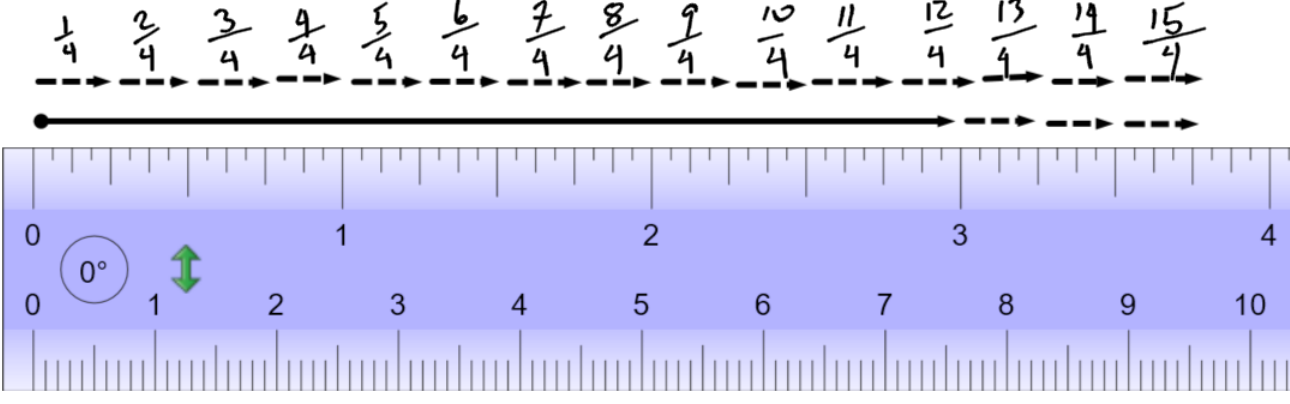
NOTE: The fraction in the mixed number is quarters, so the improper fraction is also quarters.
Example 4
Each inch has four quarters, so three inches has 3 x 4 quarters, or twelve quarters. There are an additional three quarters that are added on for a total of fifteen quarters.
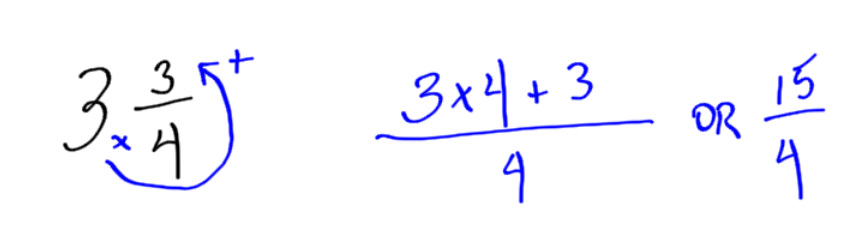
To change an improper fraction to a mixed number, multiply to find the total number of pieces, then add the remaining pieces.
4.1 – 4.2 Practice Exercises: Mixed Numbers and Improper Fractions
Change the mixed numbers to improper fractions, and the improper fractions to mixed numbers.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3 Practice Exercises Solutions:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Topic 5: Adding and Subtracting Fractions
When adding or subtracting fractions, as with anything, it only makes sense to add items that are the same. This may seem obvious in real life: 2 apples plus 3 oranges might be 5 fruit, but the answer is neither apples nor oranges. You can’t add them together because they are not the same.
Another example is money. 3 quarters and 2 dimes does not equal 5. Yes, there may be 5 coins, but we know that quarters and dimes are worth different amounts. Of course, 3 quarters and 2 dimes are 95 cents. You could only calculate that once you realize that quarters are worth 25 cents and dimes are worth 10 cents. You changed all the coins into cents, and then added the cents.
25₵ + 25₵ + 25₵ + 10₵ + 10₵ = 95₵
The same idea is true for fractions. A half a pizza is obviously not the same size as a quarter.
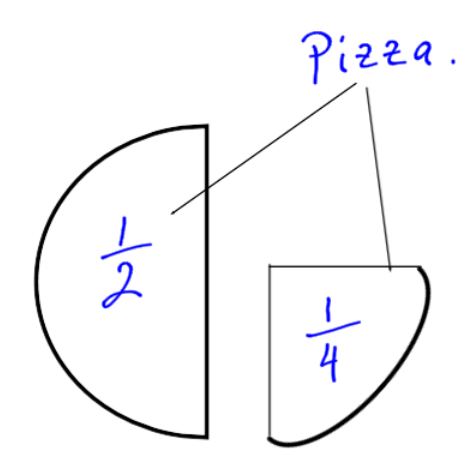
You cannot add and
to get two. There may be two pieces, but that doesn’t tell you how much pizza there is. By looking at the picture, we can see there is
of a pizza.
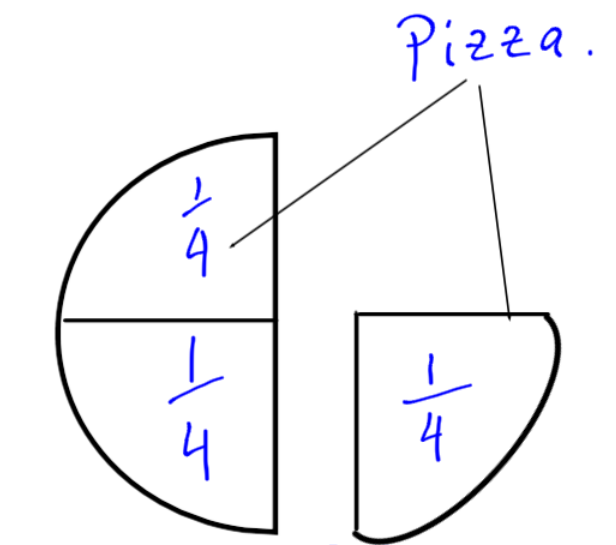
There are three pieces of pizza, and they are all the same size: one quarter.
In math speak, what we did was find a common denominator. We made the bottom numbers of the fractions and
the same. We expanded the fraction
to be
by multiplying top and bottom by two.
Example 1
Add the fractions and
|
Step |
What I am thinking |
|
Find a common denominator. |
The bottom numbers are not the same. The sizes of pieces are not the same. We need to make the pieces the same size.
|
|
Add the top numbers, keep the bottom numbers the same. |
Add the top numbers to find out how many pieces there are. The size of piece does not change. They are eighths.
|
NOTE: for tape measure fractions, it is safe to say you always turn the smaller denominator into the larger denominator.
NOTE: the larger the bottom number, the smaller the quantity.
Example 2
Subtraction happens the same way. Instead of adding the top numbers, you subtract them.
Calculate
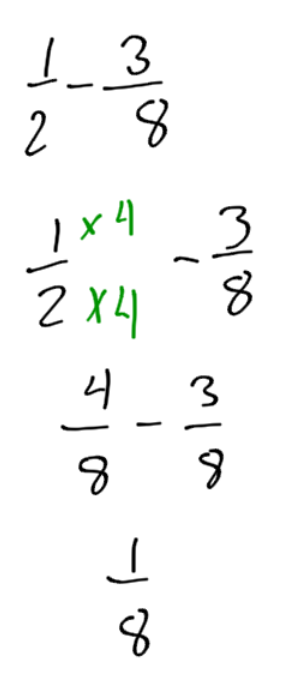
Practice Exercises: Adding and Subtracting Fractions
|
Add |
Subtract |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Practice Exercise Solutions:
|
Add |
Subtract |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Topic 6: Multiplying and Dividing Fractions
The process of multiplying and dividing fractions is more straight forward than adding and subtraction. Also, when adding or subtracting fractions, the bottom number always stays the same (you only ever add or subtract pieces of the same size.) When multiplying or dividing fractions, the bottom number may change.
6.1 Multiplying Fractions
The process is, quite simply, multiply the top numbers, and multiply the bottom numbers. You do not need to find a common denominator.
Example 1
Calculate . I am showing each step on a new line.
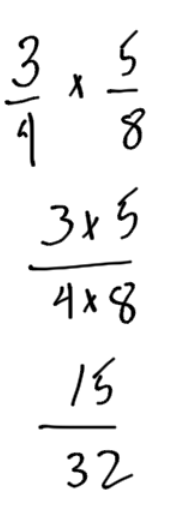
6.2 Dividing Fractions
The process of dividing fractions is to turn the division into a multiplication. The way this can be done is to “flip” the fraction on the right. Turn the fraction upside down: bottom becomes top, top becomes bottom.
Example 2
Calculate
|
Step |
What I am thinking |
|
Flip the fraction on the right. |
|
|
Multiply the two fractions. |
|
|
Simplify (reduce) the answer. |
Note: I could have just multiplied top and bottom by 4. |
6.1 – 6.2 Practice Exercises: Multiplying and Dividing Fractions
|
Multiply |
Divide |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.1 – 6.2 Practice Exercise Solutions:
|
Multiply |
Divide |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Topic 7: Fractions, Decimals, and Percent
Percent, fractions, and decimals are all related. You may know that one half is the same as “point five” (0.5). What you may not know is the reason why.
7.1 Fractions and Decimals
One half means 1 divided by two (1÷2). Try it in your calculator! Type 1÷2 and the answer will be 0.5. One way to remember this is if you look at the divide sign (÷) it looks like a fraction with a number on top, and a number on the bottom.
To convert a fraction to a decimal, divide the top of the fraction by the bottom of the fraction.
Example 1
Convert the mixed number to a decimal.
To answer this, remember that the mixed number literally means
. We know that
is 0.5. So
must be 4.5. To get this answer in your calculator, first find the decimal, then add the whole number.
|
Step |
What I am thinking |
|
Convert the fraction to a decimal. |
Enter into the calculator 1÷2= |
|
Add the whole number. |
Without clearing the calculator, press 4 + = You will get the answer 4.5 |
Example 2
To convert decimals to fractions, it helps to remember the place value names of decimals. Review Objective 1 Topic 1.
The number 0.3 is read as “three tenths.” The fraction form is like the name says:
Similarly, the number 0.56 is read as “56 one-hundredths” and is written in fraction form as . It is possible to reduce
to
. To check if this is correct, you can enter in your calculator 56÷100 and 28÷50. In both cases the answer will be 0.56.
7.1 Practice Exercises: Fractions and Decimals
1. Convert the fractions to decimals.
|
|
|
|
|
|
|
|
|
2. Convert the following decimals to fractions and reduce.
|
0.75 = |
0.5 = |
|
0.1 = |
0.9 = |
|
0.35 = |
0.125 = |
7.1 Practice Exercises Solutions:
|
1. |
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
0.75= |
0.5= |
|
0.1= |
0.9= |
|
0.35= |
0.125= |
7.2 Percent to Fraction
You may have come across a sale: “all regularly priced items are half off.” You may have also heard of a sale: “all regularly priced items are 50% (percent) off.” Both these sales are the same. The words “half off” and “50% (percent) off” mean the same thing.
We can convert a percent into a fraction. The word “percent” comes from the French words “per cent.” Cent is the French word for one hundred. So, 50% means 50 per 100 or .
You may ask how the word “half” is related to this. If you simplify (reduce) the fraction, you will end up with
(one half).
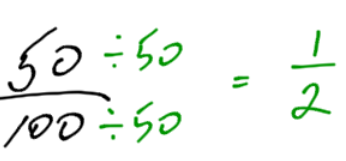
All of this may be confusing. Let’s summarize this in a table.
|
Percent |
50 per 100 |
Fraction |
1÷2= |
Decimal |
|
50% |
|
0.5 |
Example 3
Convert the following percentages to fractions and reduce.
- 75%
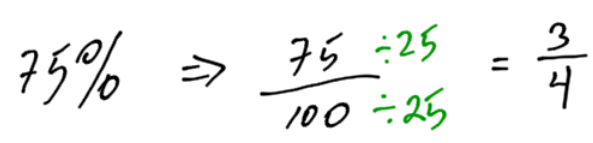
- 2%
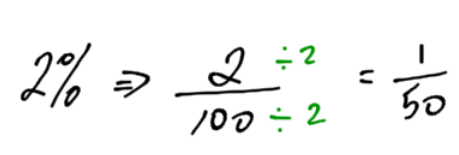
- 125%
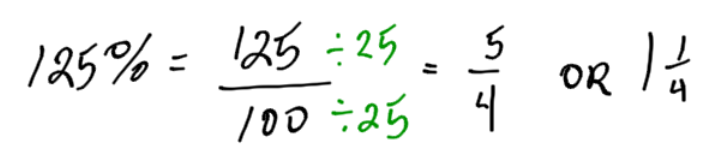
7.3 Percent to Decimal
To convert a percent directly into a decimal, divide by 100. Remember, percent means per 100: a fraction over 100.
Example 4
Convert the following percentages to a decimal:
- 50%
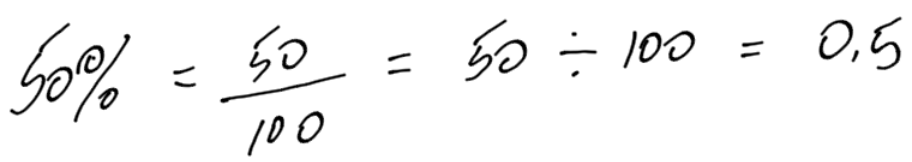
- 7%
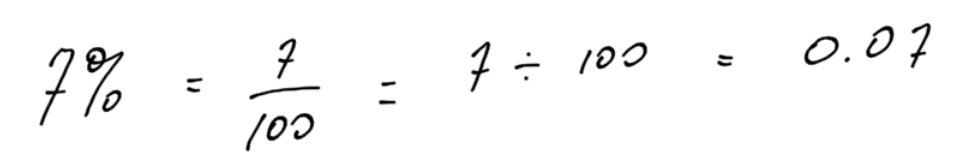
- 0.3%
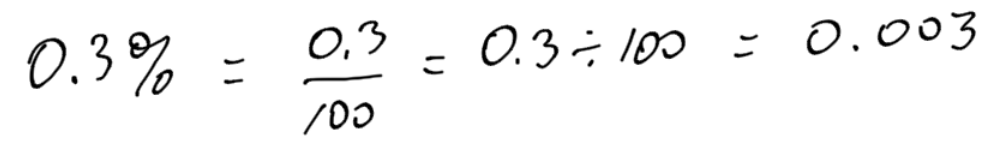
- 6.5%
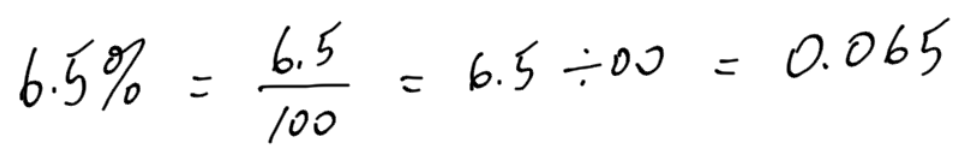
- 120%
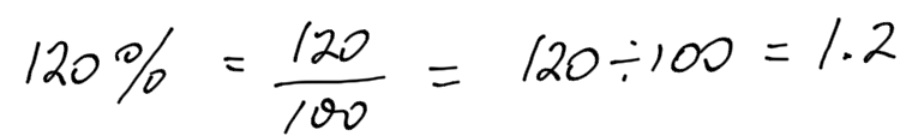
You may have noticed a pattern. The digits remain the same, but the decimal moves in each case.
When converting a percentage to a number, move the decimal twice to the left. The number will always be smaller than the percentage.
Note: if you can’t see a decimal in a number, remember there is always a decimal at the right end of the number. For example, “50” is actually “50.”.
Note: You can always add zeros to the right end of a number. For example, “6.5” can be written as “06.5”.
7.4 Decimal to Percent
Converting a decimal directly to a percent is the opposite operation as above. Division is the opposite of multiplication. In order to convert a decimal to a percent, multiply by 100.
Example 5
Convert the following numbers to percentages.
- 0.3

- 0.74
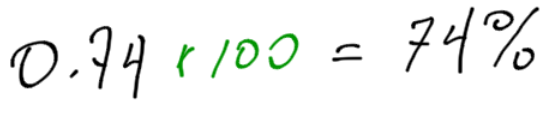
- 0.825
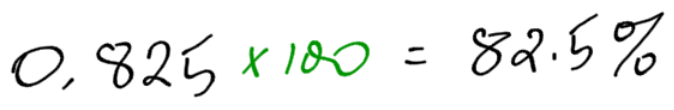
- 0.035

- 1.351

As before, you may have noticed a pattern. The digits stay the same, but the decimal moves.
When converting a number to a percentage, move the decimal twice to the right. The percentage will always be larger than the number.
7.5 Fraction to Percent
Example 6
Convert the following fractions to percentages.
When converting a fraction to a percent, you have to convert the fraction to a decimal, and the decimal to a percent.
|
Fraction |
1÷2= |
Decimal |
0.5 X 100 =
|
Percent |
|
12 |
0.5 or five tenths
|
50% |
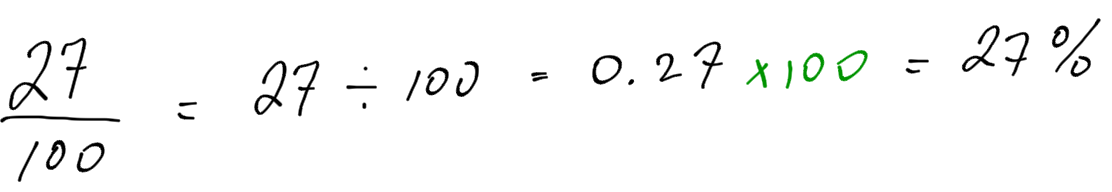
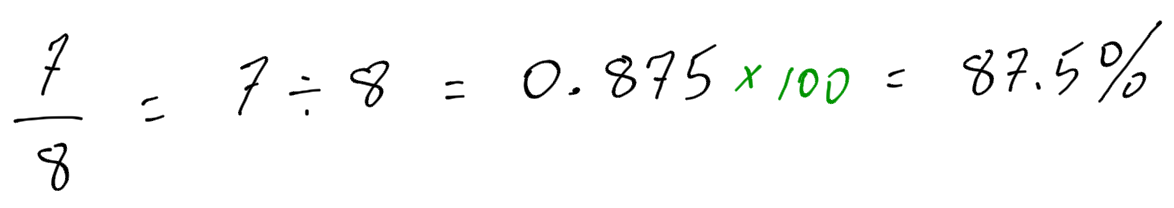
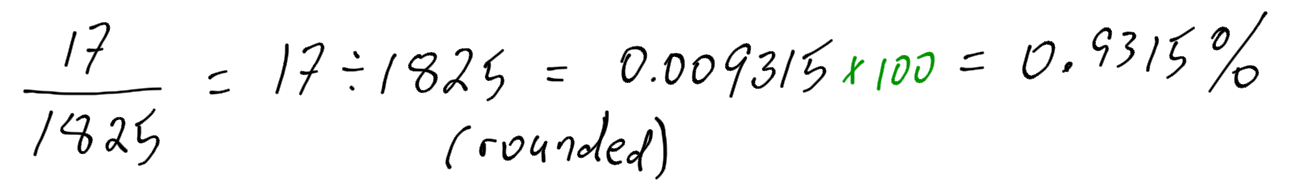
7.6 Scenarios
Percentages, decimals and fractions are used every day in real life. Here are some scenarios where you might use them.
Example 7
You may have heard the advertising claim “4 out of 5 dentists recommend a toothpaste.” What percentage of dentists recommend the toothpaste?
4 out of 5 represents a fraction: . We need to convert this fraction to a decimal number, and then to a percentage.
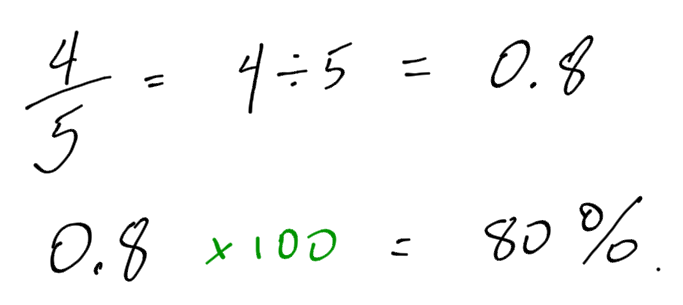
80% of dentists recommend the toothpaste.
Example 8
At a convention of 350 dentists, how many dentists from the previous question recommend the toothpaste?
Eighty percent of dentists recommend the toothpaste. The word of is a keyword. It means multiply. We need to multiply 350 dentists X 80%. In order to multiply this, we need to convert 80% into a decimal.
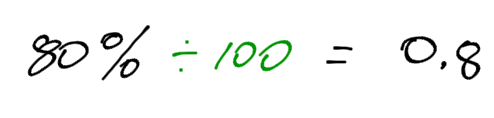
Now, multiply the 350 dentists by 0.8.
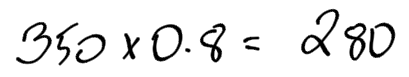
280 dentists at the convention recommended the toothpaste.
Review Exercises: Fractions, Decimals and Percentages
|
|
Fraction |
Decimal |
Percent |
|
1. |
|
|
|
|
2. |
|
|
50% |
|
3. |
|
|
40% |
|
4. |
|
0.375 |
|
|
6. |
|
|
60% |
|
7. |
|
0.1 |
|
1. At a construction job for a store there are 20 painters. Of these painters, 15 of them are painting the interior of the store. What percent of these painters are painting the interior? Round your answer to the nearest whole number if necessary.
2. Sara decided to look at new and used cars. Sara found a used car for $30,000. A new car is $50,000, so what percent of the price of a new car does Sara pay for a used car? Round your answer to the nearest whole number if necessary.
3. One baseball team played 35 games throughout their entire season. If this baseball team won 80% of those games, then how many games did they win? Round your answer to the nearest whole number if necessary.
4. Joan receives a $35,000 salary for working as an administrator. If Joan spends 80% of her salary on expenses each year, then how much money does Joan have to spend on expenses? Round your answer to the nearest whole number if necessary.
5. At a local department store, sweaters are typically priced at $40. Due to a special, the sweaters are reduced to 95% of their original price. How much are sweaters now? Round your answer to the neatest whole number if necessary.
6. A large metal bar that weighed 20 grams. Sally was also able to determine that the bar contained 50% zinc. How many grams of zinc are in the metal bar? Round your answer to the nearest whole number if necessary.
7. Joan went to her local zoo that featured 30 bird exhibits. If the zoo features 50 exhibits in total, then what percent of the zoo’s exhibits feature birds? Round your answer to the nearest whole number if necessary.
8. In one particular suburb, there are 6 families that own a shih tzu. If there are a total of 15 families that own a dog in general, then what percentage of dog owners have a shih tzu? Round your answer to the nearest whole number if necessary.
9. For one biology test, Keith had to answer 25 questions. Of these 25 questions, Keith answered 5 of them correctly. What percent did Keith get on his biology test? Round your answer to the nearest whole number if necessary.
10. There are 15 students in a class and 60% of these students passed their algebra test. What number of these students passed their test? Round your answer to the nearest whole number if necessary.
Review Exercise Solutions:
Part 1
|
|
Fraction |
Decimal |
Percent |
|
1. |
|
|
|
|
2. |
|
|
50% |
|
3. |
|
|
40% |
|
4. |
|
0.375 |
|
|
6. |
|
|
60% |
|
7. |
|
0.1 |
|
Part 2
1. 75%, 2. 60%, 3. 28 grams, 4. $28000, 5. $38, 6. 10 grams, 7. 60%, 8. 40%, 9. 20%, 10. 9 students.
Outcome 2 Test (1h)
Complete Essentials 1 Math: Fractions, Decimals and Percentages Chapter Quiz on Brightspace.