7 Geometry
Section Information
Outcome/Competency: You will be able to model and calculate scenarios in two- and three-dimensions using geometry.
Timing: 26h
Rationale: Why is it important for you to learn this skill?
Geometry is the study of shapes. Being able to calculate volume and area of a shape, for example, is very important in calculating supplies required for building.
Objectives:
To be competent in this area, the individual must be able to:
- Demonstrate understanding of perimeter, area of 2-D shapes, and surface area and volume of 3-D objects including units in SI and Imperial systems of measurement
Learning Goals
- Model, calculate, interpret, and solve problems in two and three dimensions by using different representations and manipulating formulae
- Apply conversion factors using unit analysis and calculation to solve scenarios and situational problems
Introduction:
In this section you will learn about circumference, diameter, radius, area, surface area, and volume. You’ll be presented with concepts and examples, and given opportunities to practice throughout.
Chapter Contents:
- Topic 1: Perimeter and Circumference
- Topic 2: Area
- Topic 3: Surface Area
- Topic 4: Volume
- Test: Outcome 7
Topic 1: Perimeter and Circumference
We can make use of conversion skills with denominate numbers to make measurements of geometric figures such as rectangles, triangles, and circles. To make these measurements we need to be familiar with several definitions.
1.1 Polygons
A polygon is a closed plane (flat) figure whose sides are line segments (portions of straight lines).
|
Polygons
|
Not polygons
|
1.2 Perimeter
The perimeter of a polygon is the distance around the polygon. To find the perimeter of a polygon, we simply add up the lengths of all the sides.
Example 1
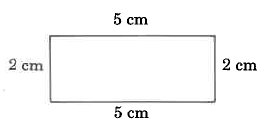
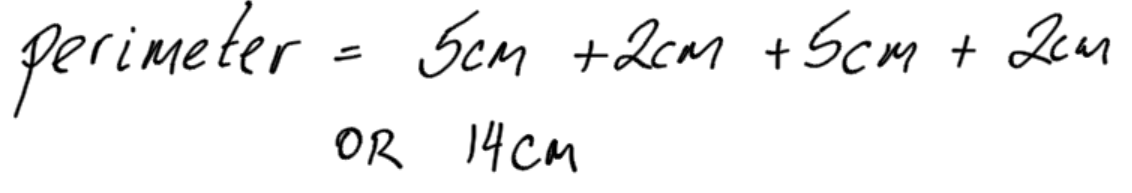
 Don’t be tempted to memorize a formula for this. Some people may think that they should memorize a formula such as: Perimeter = 2X length + 2 X width. This type of memorization is unnecessary if you simply remember the perimeter is the sum of all the sides.
Don’t be tempted to memorize a formula for this. Some people may think that they should memorize a formula such as: Perimeter = 2X length + 2 X width. This type of memorization is unnecessary if you simply remember the perimeter is the sum of all the sides.
Example 2
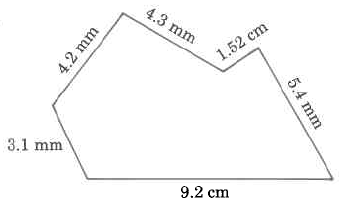
The sides do not need to be going perpendicular or parallel to each other. In this irregular shape, to find the perimeter, you still need to add all the sides.
 When adding measurements together, they must be in the same units. Notice some of the units are in mm, and some in cm. There are 10 mm in 1 cm.
When adding measurements together, they must be in the same units. Notice some of the units are in mm, and some in cm. There are 10 mm in 1 cm.

Example 3
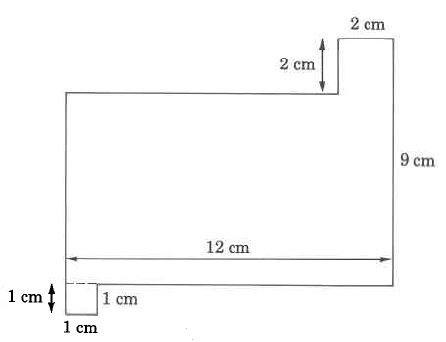
In some regular shapes you will need to figure out unknown measurements based on other given measurements. Find the sides labeled A, B and C.
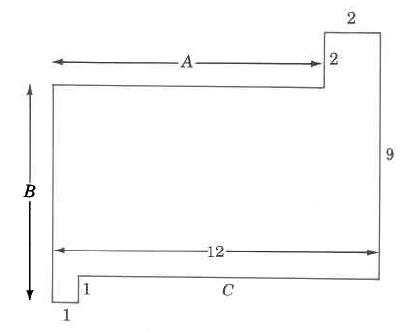
If the measurements you need are across the shape, it is sometimes useful to visualize them all together like in this diagram:
Consider side A:
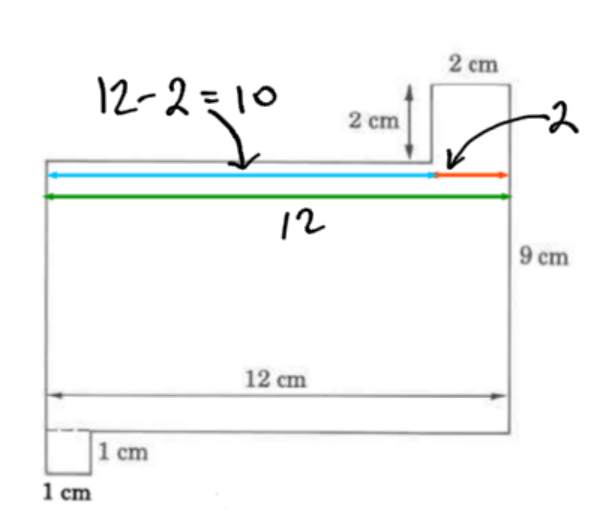
The unknown top side, A (blue), is 10 cm long.
Consider side B:
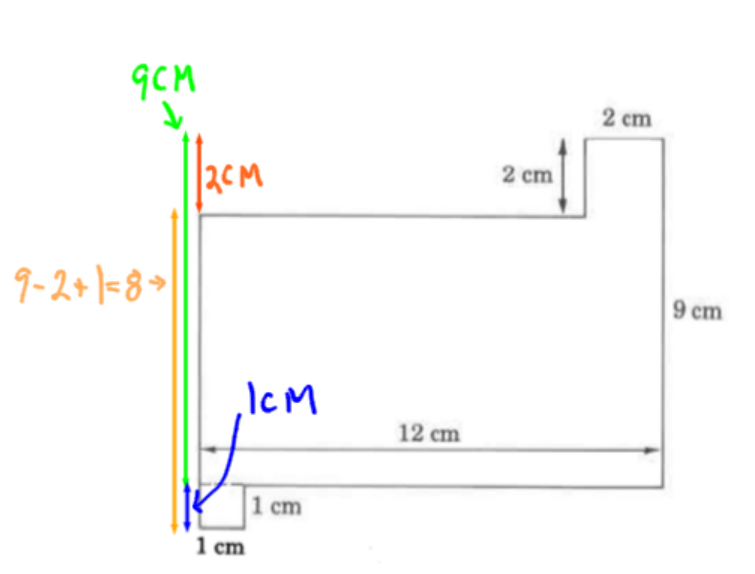
The unknown side B (yellow), is 8 cm.
Consider unknown side C:
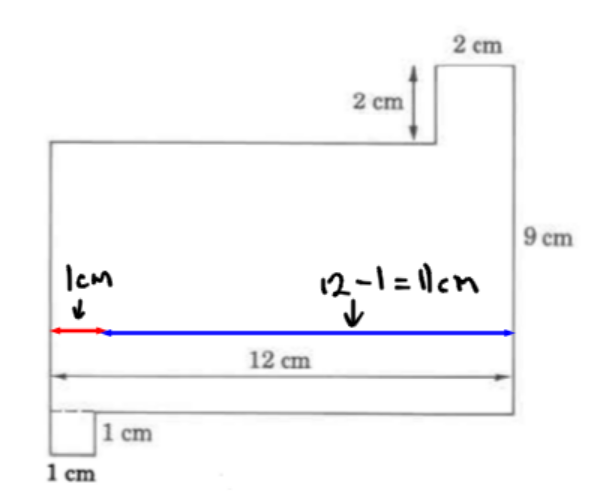
The unknown side, C (blue), is 11 cm long.
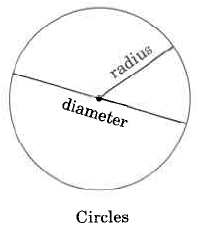
1.3 Circumference/Diameter/Radius
Circumference
The circumference of a circle is the distance around the circle. In plain language, the circumference is the perimeter of a circle.
You could measure the circumference of a circle with a string, but if you wanted to calculate the circumference, you need to use a formula. The formula depends upon one of two measurements: the diameter, or the radius.
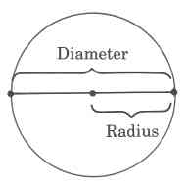
Diameter
A diameter of a circle is any line segment that passes through the center of the circle and has its endpoints on the circle.
Radius
A radius of a circle is any line segment having as its endpoints the center of the circle and a point on the circle. The radius is one half the diameter.
1.4 The Number π
The symbol π, read “pi,” represents the nonterminating, nonrepeating decimal number 3.14159 … . This number has been computed to millions of decimal places without the appearance of a repeating block of digits.
For computational purposes, π is often approximated as 3.14. We will write π≈3.14 to denote that π is approximately equal to 3.14. The symbol “≈” means “approximately equal to.”
When doing calculations on your calculator with a pi button you should use it, and round the answer after. Here is the pi button:

1.5 Circumference of a Circle
To find the circumference of a circle, we need only know its diameter or radius. We then use a formula for computing the circumference of the circle. Formulas are usually composed of letters that represent important, but possibly unknown, quantities.
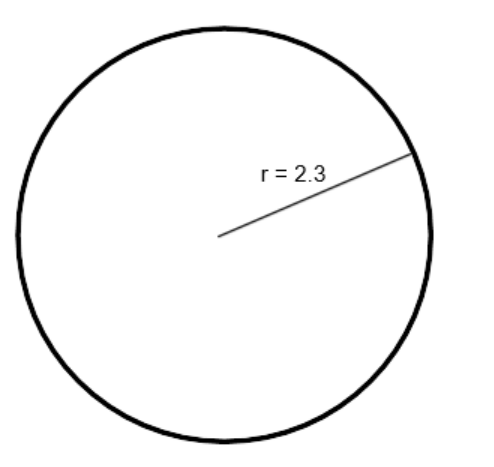
C=2πr
OR
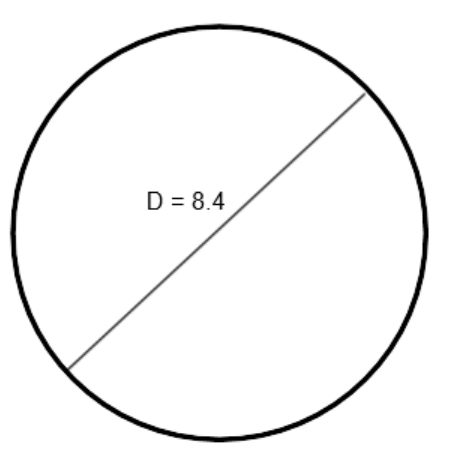
C=πD
Example 4
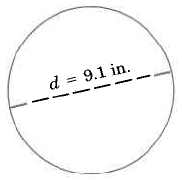
Find the circumference of the circle:
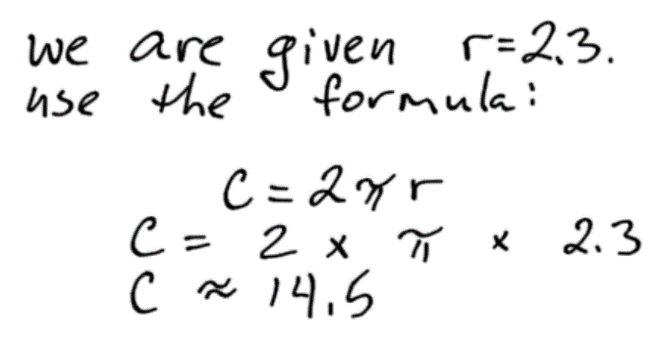
Example 5
Find the circumference of the circle:
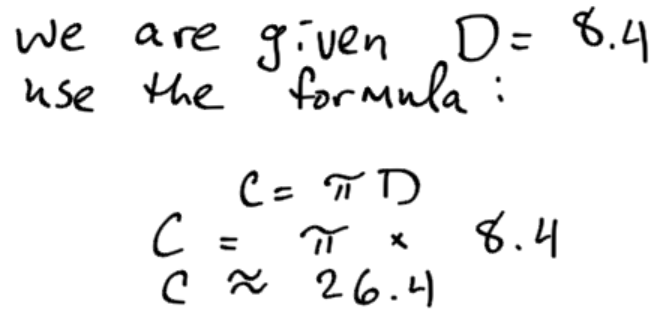
Practice Exercises: Perimeter and Circumference
- Find the perimeter of the shapes below:
a)
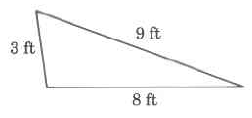
b)
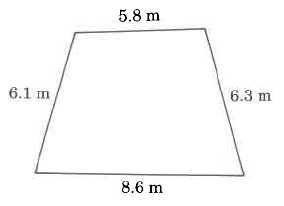
c)
d)
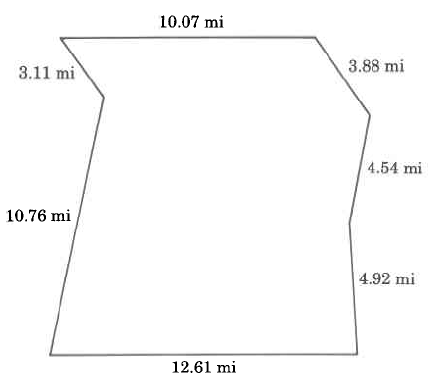
2. Extension Question: Find the perimeters of the following figures
a)
Solution:
1. a) 20 ft.
b) 26.8 m
c) 49.89 mi
d) 28.6 in
2. a) 74mm
Topic 2: Area
The area of a surface is the amount of square length units contained in the surface.
For example, 3 sq in. means that 3 squares, 1 inch on each side, can be placed precisely on some surface. (The squares may have to be cut and rearranged so they match the shape of the surface.)

2.1 Finding Areas of Some Common Geometric Figures
We will examine the area of the following geometric figures:
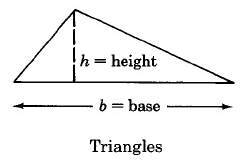
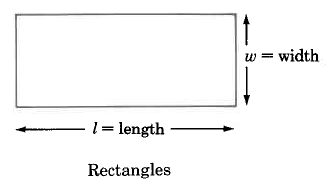
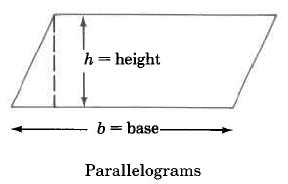
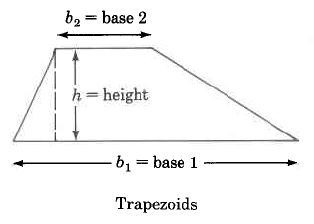
We can determine the areas of these geometric figures using the following formulas.
|
|
Figure |
Area Formula |
Statement |
|
|
Triangle |
A=1/2×b×h |
Area of a triangle is one half the base times the height. |
|
|
Rectangle |
A=l×w |
Area of a rectangle is the length times the width. |
|
|
Parallelogram |
A=b×h |
Area of a parallelogram is base times the height. |
|
|
Trapezoid |
A=(b1+b2)/2×h |
Area of a trapezoid is one half the sum of the two bases times the height. |
|
|
Circle |
A=π×r2 |
Area of a circle is ππ times the square of the radius. |
 Remember, when calculating “one half” or “over two” the way to type that in the calculator is using the divide button. For example, “one half the base times the width” in your calculator is base × width ÷ 2.
Remember, when calculating “one half” or “over two” the way to type that in the calculator is using the divide button. For example, “one half the base times the width” in your calculator is base × width ÷ 2.Example 1
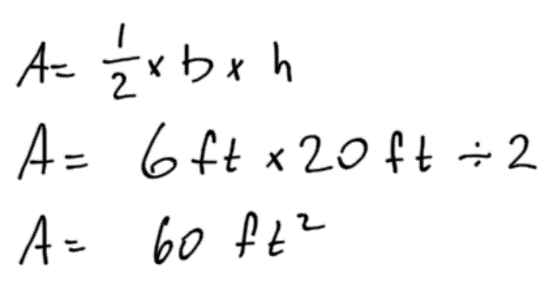
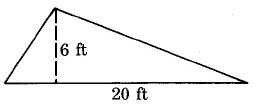
Note that feet multiplied by feet give ft2 pronounced as “feet squared.” (The unit is squared; this does not mean square the number.) Whenever a unit is squared, it is a unit of area.
Example 2
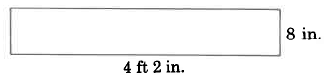
In this example, we need to convert 4 ft 2 in into units of inches. You cannot mix different units when finding area. There are 12 inches per foot.
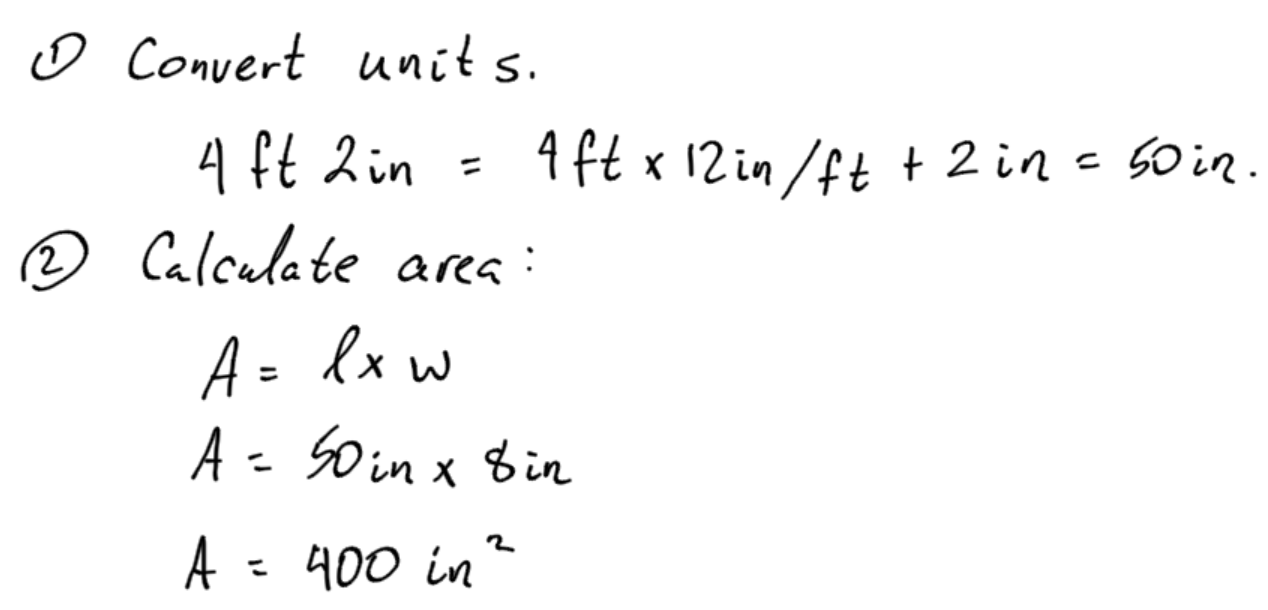
Example 3
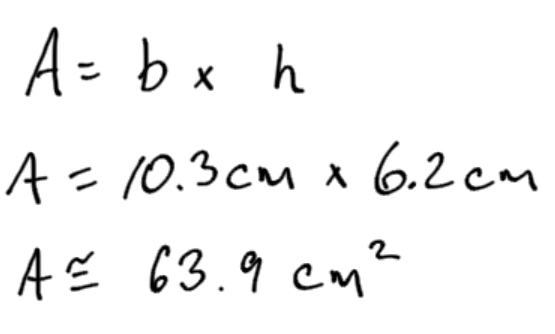
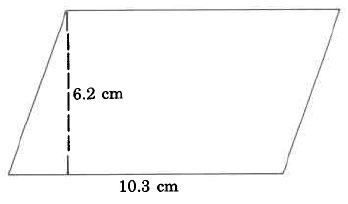
Example 4

In this case, call the bottom b1 and the top b2, but the labeling doesn’t matter in this case. The top could be called b1 and the bottom b2.
When using the calculator, “over 2” means divide by 2.
A note about order of operations: In this calculation, the 20.4 and 14.5 need to be added before the sum can be divided by 2. There are two ways to accomplish this:
- Use brackets on your calculator to calculate 20.4 + 14.5 before dividing by 2
- Use the equal sign after 20.4 + 14.5. Once the equal sign is pressed, the numbers are added, and you can divide the total by 2.
The sample calculation below uses brackets.
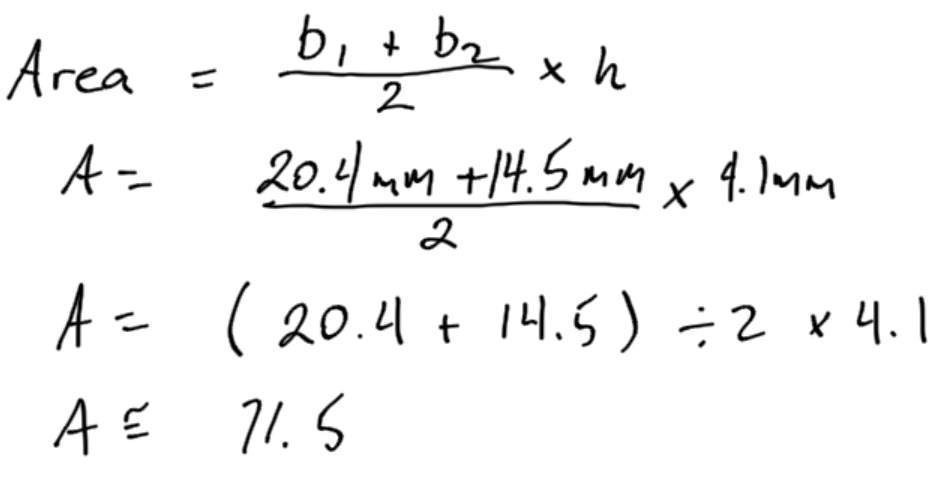
Example 5
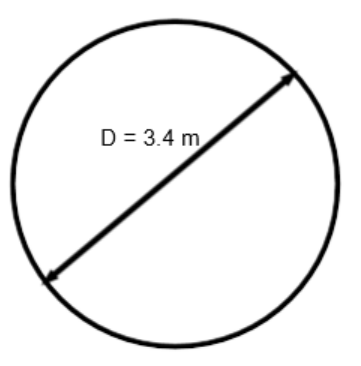

In this example, the diameter is given. The area formula for a circle calls for radius. We must convert the diameter into a radius by dividing it in half before using it in the formula.
Example 6

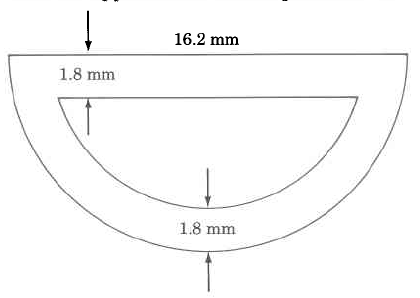
In some questions, it is necessary to find a total area, and subtract an inner area. In this example, to find the shaded area, we can find the area of the larger rectangle and subtract the area of the smaller rectangle.

2.2 Areas of Parallelograms and Triangles
A parallelogram is a quadrilateral (it has four sides). The opposite sides of a parallelogram are parallel. It is also true that:
- the opposite sides of a parallelogram have equal length, and
- the opposite angles of a parallelogram have equal measure.
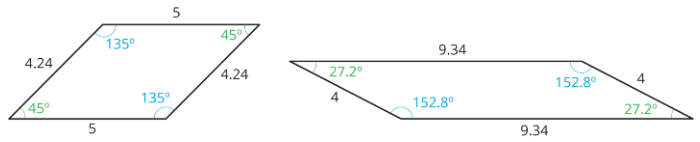
There are several strategies for finding the area of a parallelogram.
1. We can decompose and rearrange a parallelogram to form a rectangle.

2. We can enclose the parallelogram and then subtract the area of the two triangles in the corner.
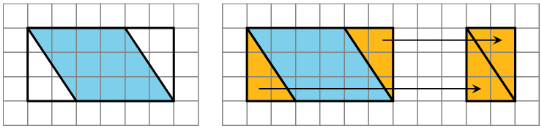
Both ways will work for any parallelogram. However, for some parallelograms the process of decomposing and rearranging requires a lot more steps than if we use a formula. Using a formula is a good shortcut, but if you don’t remember the formula, you can always rely on your ability to manipulate the image and use simpler formulas that you remember.
A parallelogram can always be decomposed into two identical triangles by a segment that connects opposite vertices.
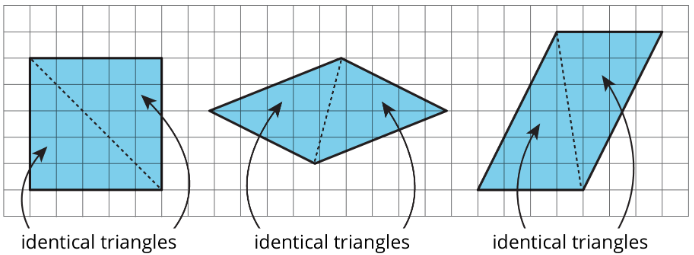
Going the other way around, two identical copies of a triangle can always be arranged to form a parallelogram, regardless of the type of triangle being used.
To produce a parallelogram, we can join a triangle and its copy along any of the three sides, so the same pair of triangles can make different parallelograms.
Here are examples of how two copies of both Triangle A and Triangle F can be composed into three different parallelograms.
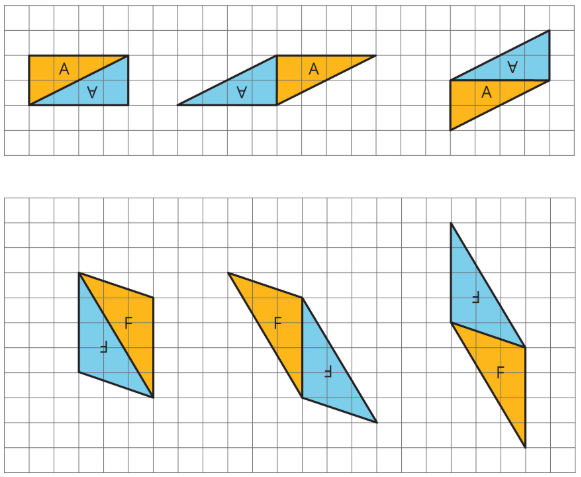
This special relationship between triangles and parallelograms can help us reason about the area of any triangle. If the area of a parallelogram is base times height, then it makes sense that the area of a triangle (which is half a parallelogram) is one half of the base times height.
Area of Parallelogram = b x h
Area of Triangle = 1/2 x b x h
Practice Exercises: Area
1. Are these statements true or false?
– A parallelogram has six sides.
– Opposite sides of a parallelogram are parallel.
– A parallelogram can have one pair or two pairs of parallel sides.
– All sides of a parallelogram have the same length.
– All angles of a parallelogram have the same measure.
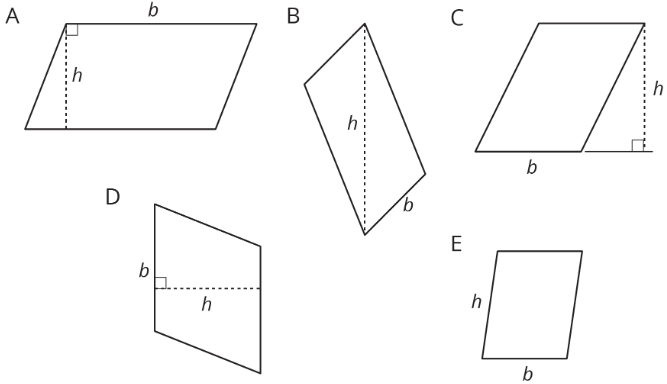
2. Five students labeled a base b and a corresponding height h for each of these parallelograms. Are all drawings correctly labeled? Explain how you know.
3. Find the area of the following shapes:
a. 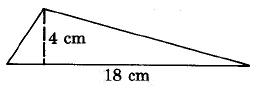 b.
b.
c.
d.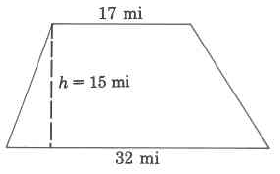 e.
e.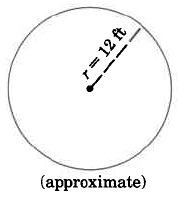
f.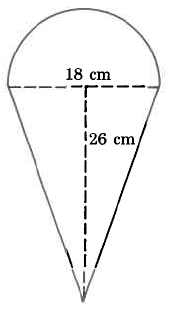 g.
g.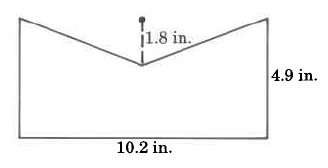
i. (Assume the following shape is vertically symmetric about the center.
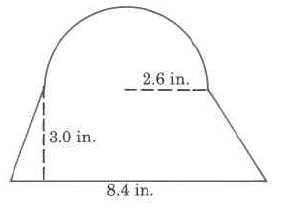 i.
i.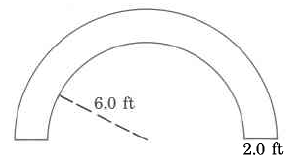
Solution:
1. F, T, F, F, F.
2. B and E are incorrect.
3. a) 36
b) 9.72
c) 13.26
d) 367.5
e) 452.4
f) 595
g) 40.8
h) 31.02
i) 44
Topic 3: Surface Area
Surface area is the combined area of all the sides of a three dimensional shape.
Polyhedra
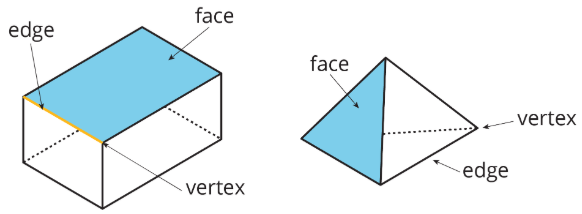
A polyhedron is a three-dimensional figure composed of faces. Each face is a filled-in polygon and meets only one other face along a complete edge. The ends of the edges meet at points that are called vertices.
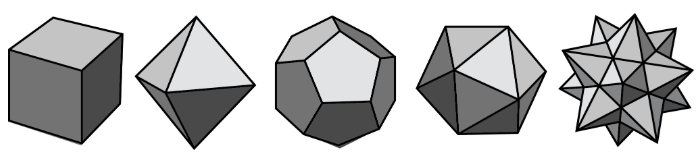
Polyhedra always encloses a three-dimensional region.
Here are pictures that represent polyhedra:
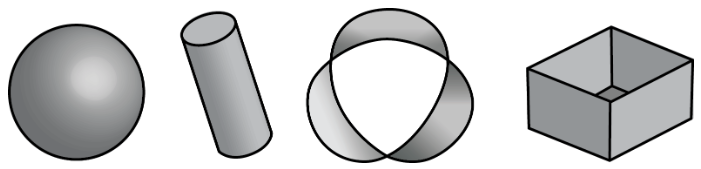
Here are pictures that do not represent polyhedra:
The surface area of a polyhedron is the sum of the areas of all the faces.
Because a net shows us all faces of a polyhedron at once, it can help us find the surface area. We can find the areas of all polygons in the net and add them.
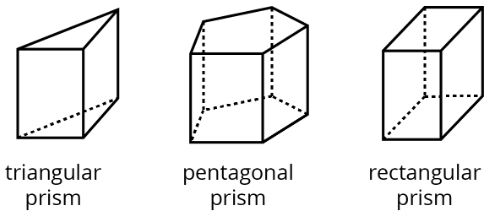
A prism is a type of polyhedron with two identical faces that are parallel to each other and that are called bases. The bases are connected by a set of rectangles (or sometimes parallelograms).
A prism is named for the shape of its bases. For example, if the base is a pentagon, then it is called a “pentagonal prism.”
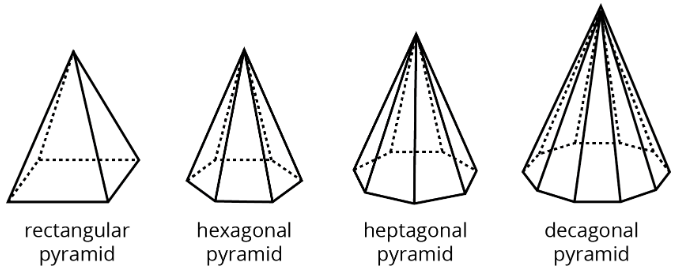
A pyramid is a type of polyhedron that has one special face called the base. All the other faces are triangles that all meet at a single vertex.
A pyramid is named for the shape of its base. For example, if the base is a pentagon, then it is called a “pentagonal pyramid.”
A net is a two-dimensional representation of a polyhedron. It is composed of polygons that form the faces of a polyhedron.
In a cube, every face shares its edges with 4 other squares. In a net of a cube, not all edges of the squares are joined with another edge. When the net is folded, however, each of these open edges will join another edge.
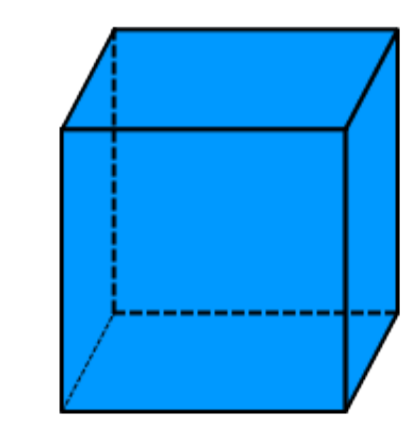
13. cube with 6 identical faces
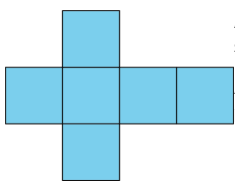
14. The net of the cube. Each side is connected by one shared line.
A net can be cut out and folded to make a model of the polyhedron.
Example 1
Find the surface area of this square pyramid.
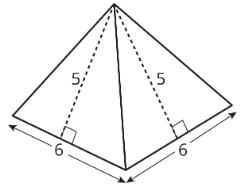
It is useful to help visualize all the sides flat. Then, the question just becomes finding the area of a bunch of basic shapes. Draw a net for the figure like so:
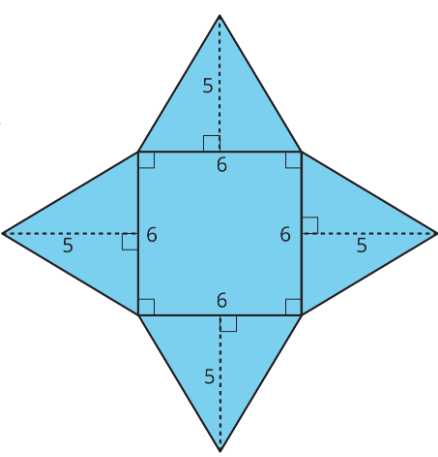
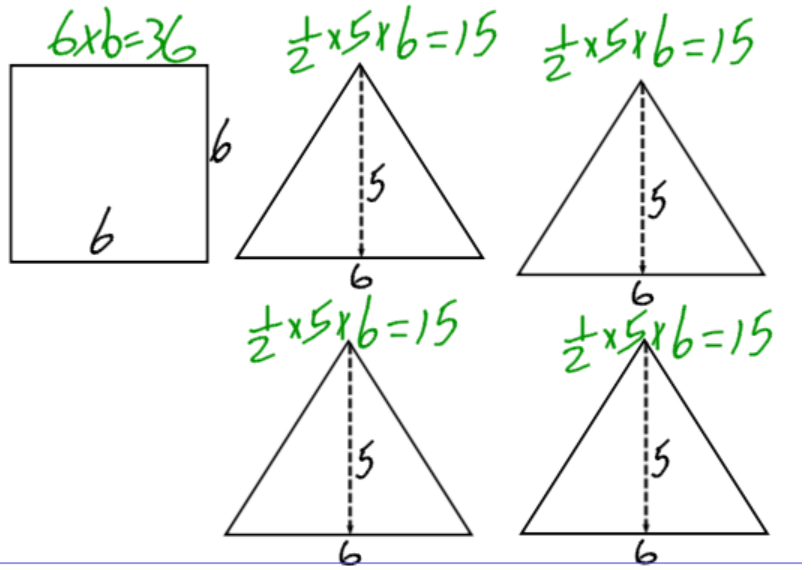
A square pyramid has a square and four triangles for its faces. Its surface area is the sum of the areas of the square base and the four triangular faces:
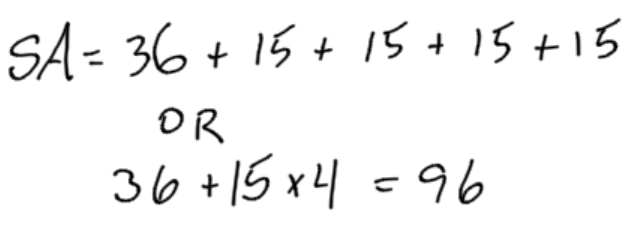
The surface area of this square pyramid is 96 square units.
A cylinder is a 3 dimensional shape that has a circular base.
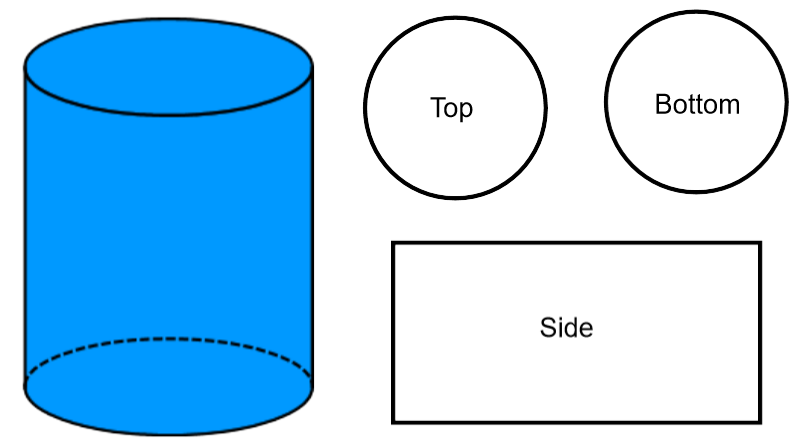
As seen in the diagram, the sides of the cylinder can be drawn as two circles for the top and bottom, and a rectangular side. The surface area of a cylinder is total area of the two circles and rectangle.
Example 2
Find the surface area of the following cylinder
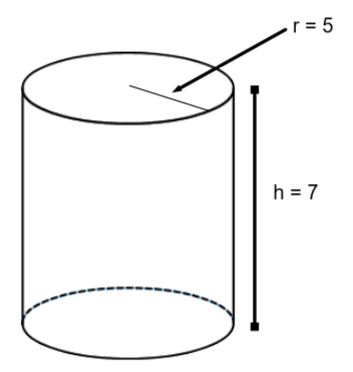
The cylinder can be broken down into the following circles (for top and bottom) with radius 5:
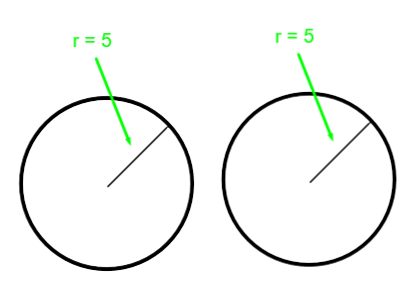
The area of one circle comes from the formula πr2
Area= πr2
Area= π×52≈ 79
Finding the dimensions of the side involves a trick. The height is obviously 7, from the original diagram. The width is the circumference of the circle. (Remember, the formula for the circumference is
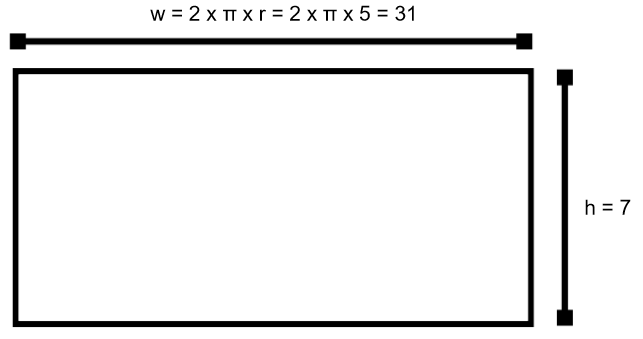
To calculate the width, us the formula for the circumference of the top or base: 2πr.
circumference=2πr
width=2×π×5≈31
The area of the rectangle is the length times the width:
7×31=217
The total area of the sides of the cylinder:
total surface area=area top+ area bottom +area side
total surface area=79+79+217
total surface area= 375
Practice Exercises: Surface Area
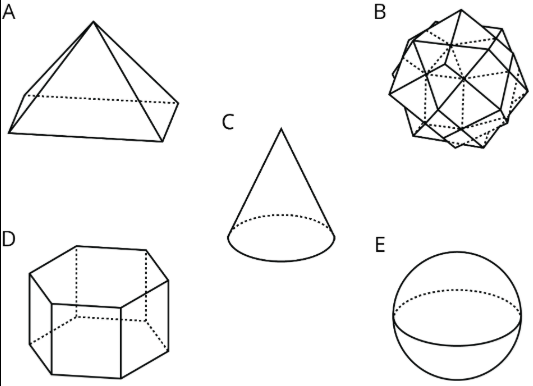
1. Which of the following shapes represent a polyhedron?
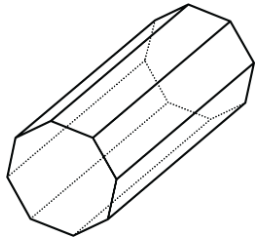
2. Is this polyhedron a prism, a pyramid, or neither? Explain how you know.
3. Here are two polyhedra and their nets. Label all edges in the net with the correct lengths. Find the surface area of polyhedron A.
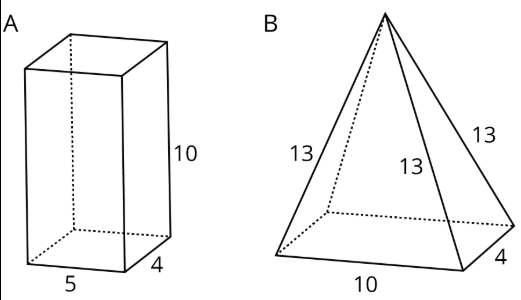
Challenge Question: Find the surface area of polyhedron B. (Hint: you will need to use Pythagoras’ Theorem to find the heights of the triangles.)
4. Calculate the surface area of the following cylinder
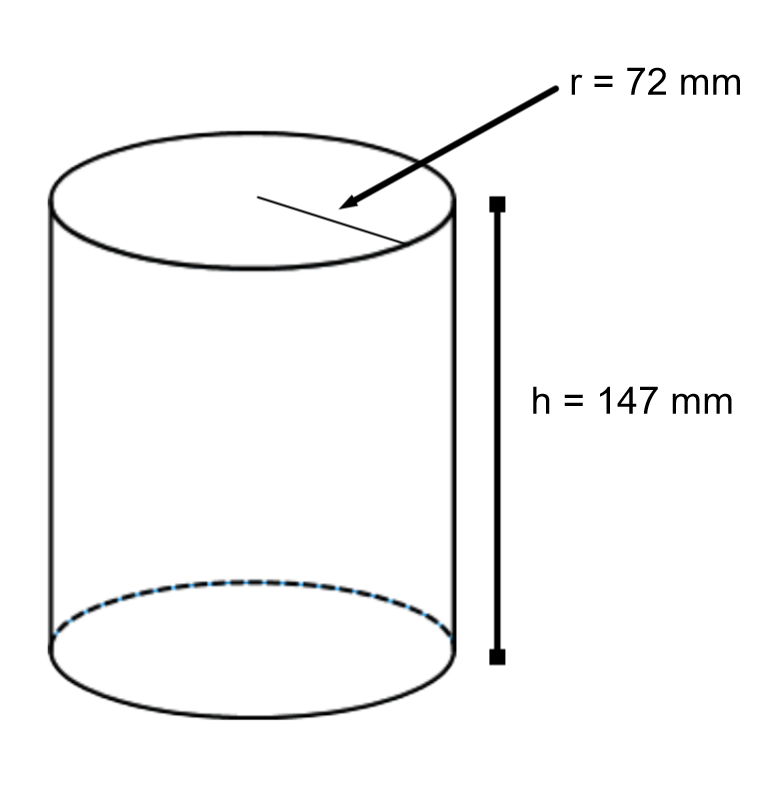
Solution:
1. A, B, D
2. Prism because does not come to a tip, sides are not triangles.
3. Surface area A = 220. Surface area B = 141
4. Surface area = 99,073 square mm.
Topic 4: Volume
The product (length unit) x (length unit) x (length unit) = (length unit)3, or cubic length unit (cu length unit), can be interpreted physically as the volume of a three-dimensional object.
For example, 4 cu mm means that 4 cubes, 1 mm on each side, would precisely fill some three-dimensional object. (The cubes may have to be cut and rearranged, so they match the shape of the object.)
Volume Formulas
|
|
Figure |
Volume Formula |
Statement |
|
|
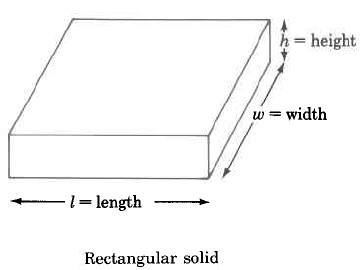
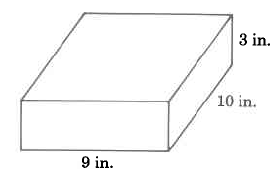
Rectangular solid |
V=l×w×h |
The volume of a rectangular solid is the length times the width times the height. |
|
|
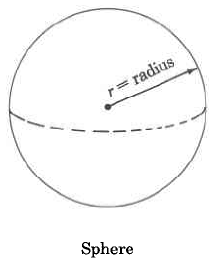
Sphere |
V=4/3 πr3 |
The volume of a sphere is 43size 12{ { {4} over {3} } } {} times ππ times the cube of the radius. |
|
|
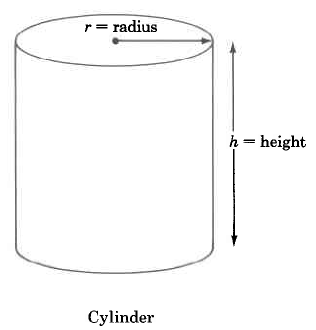
Cylinder |
V=πr2h
|
The volume of a cylinder is ππ times the square of the radius times the height. |
|
|
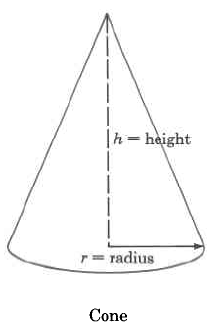
Cone |
V=1/3 πr2h |
The volume of a cone is 13size 12{ { {1} over {3} } } {} times ππ times the square of the radius times the height. |
Example 1
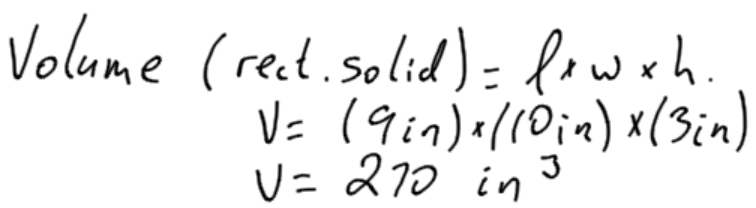
Example 2
Find the volume of this sphere:
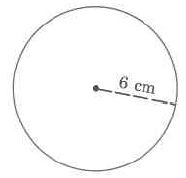
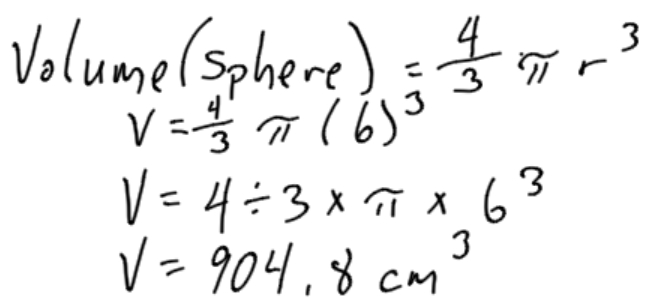
Example 3
Find the volume of this cylinder:
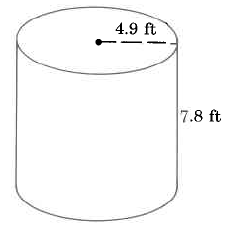
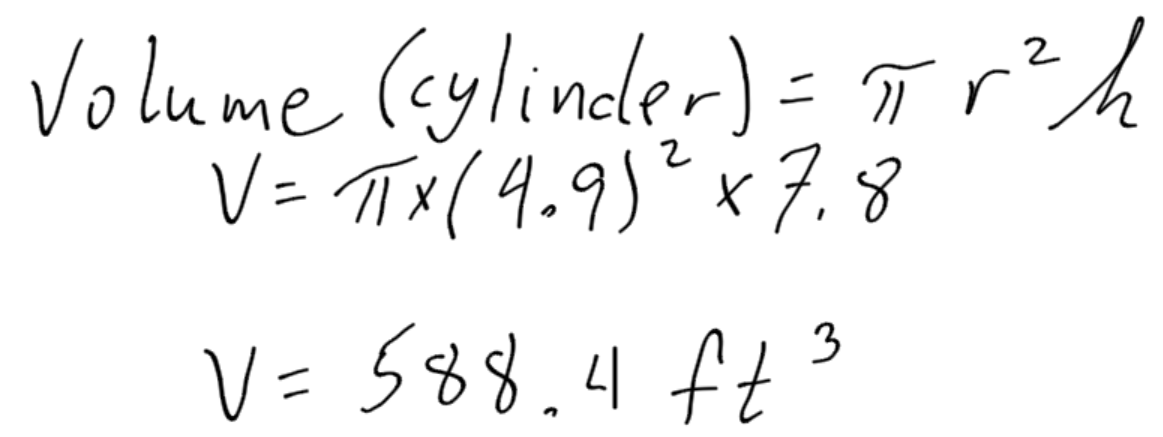
Example 4
Find the volume of this cone:
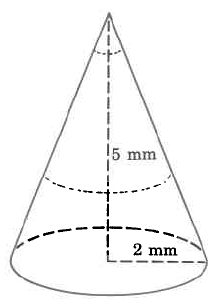
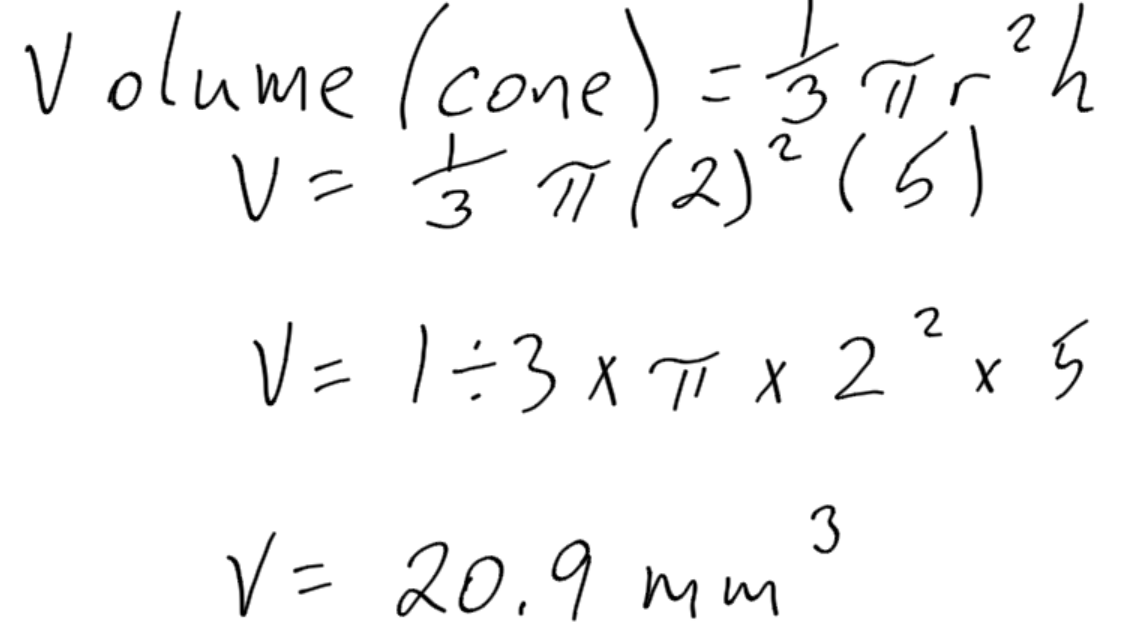
Practice Exercises: Volume
1. Find the volume of the following shapes:
a.
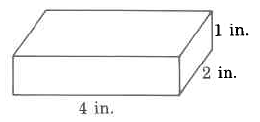
b.
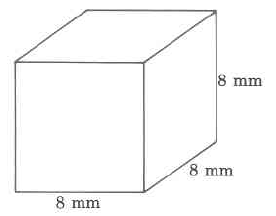
c.
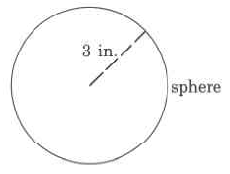
d.
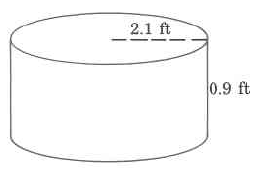
e.
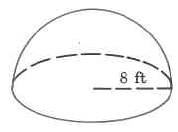
f.
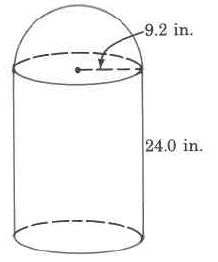
g.
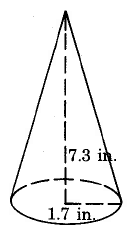
h.

Solution:
1. a) 8
b) 512
c) 113
d) 12.5
e) 1072
f) 8012.6
g) 22
h) 64.3
Outcome 7 Test
Complete the Essentials 1 Math: Geometry Chapter Quiz on Brightspace.