VIII. Técnicas dos séculos XX e XXI
Conxuntos de clases de altura, orde normal e transformacións
Brian Moseley and Megan Lavengood
Puntos principais
- Un conxunto de clases de altura é un grupo de clases de altura.
- A maneira estándar de dar nome aos conxuntos de clases de altura é a orde normal: a disposición máis pequena posible das clases de altura, en orde ascendente.
- Para traspor un conxunto (Tn), hai que sumar n a cada número enteiro do conxunto.
- Para inverter un conxunto (In), primeiro cómpre inverter o conxunto (tomar o complemento mod 12 de cada número enteiro), e despois traspor á distancia n. En vez diso, podemos subtraer cada número enteiro do conxunto de n (n–x=y).
- O reloxo pode axudar para realizar estas tarefas.
Conxuntos de clases de altura
Cando falamos dun grupo de clases de altura como unidade, chamámolo conxunto de clases de altura, (en inglés pitch-class set, abreviado como “pc set“). Calquera grupo de clases de altura pode ser un conxunto de clases de altura.
Orde normal
A orde normal (normal order) é a forma máis comprimida dunha colección de clases de altura, en orde ascendente. A orde normal ten moito en común co concepto do estado fundamental. O estado fundamental é a maneira stándar de ordenar as clases de altura das tríades e acordes de sétima para podermos clasificalos e comparalos doadamente. A orde normal é o mesmo, pero de xeito máis xeneralizado, de modo que se aplica aos acordes que conteñen unha variedade de notas e intervalos.
A seguir, describimos un método matemático e outro visual para determinarmos a orde normal.
Método matemático
| Proceso | Conxunto de exemplo: Sol♯4, La2, Re♯3, La4 |
| 1. Escribe a colección de clases de altura (eliminando duplicidades) de modo que encaixen nunha soa oitava se os tocásemos en orde ascendente. Hai varias opcións posibles, escolle unha. | 8,9,3 |
| 2.Duplica a primeira altura ao final. | 8,9,3,8 |
| 3. Acha o intervalo ordenado de maior tamaño entre clases de altura adxacentes | de 8 a 9: 1 de 9 a 3: 6 de 3 a 8: 5 o intervalo máis grande é de 9 a 3. |
| 4. Reescribe a colección comezando coa clase de altura que estea á dereita do intervalo de maior tamaño e escribe a resposta entre corchetes. | [3,8,9] |
Ás veces, haberá empate entre candidatos a intervalo de maior tamaño no punto 3. Nestes casos, a ordenación que sexa máis compacta a un lado ou outro é a forma normal. Se aínda hai empate, escolle o conxunto que sexa máis compacto á esquerda.
Método visual (o método do reloxo)
Se non che gusta o proceso que acabamos de describir, o vídeo do exemplo 1 (en inglés) explica de forma clara como usar un reloxo para encontrar axiña a orde normal. [podes abrilo nun novo separador/lapela co botón dereito do rato]
https://coursemedia.gmu.edu/embed/secure/iframe/entryId/1_axkf6ow8/uiConfId/+44431031/st/0
Exemplo 1. Using the clock face to find normal form.
Transposición
Na música postonal, a transposición asóciase moitas veces ao movemento: se tes un acorde, motivo ou melodía, e aplicas unha transposición, o efecto auditivo que produce é que se move ese acorde, motivo ou melodía nalgunha dirección. En dúas pasaxes desconexas de La cathédrale engloutie de Claude Debussy, o motivo inicial <Re, Mi, Si> ou <2, 4, 11> é trasposto catro semitóns ascendentes, a <Fa♯, Sol♯, Re♯> ou <6, 8, 3> no compás 18 (os dous aparecen en azul no Exemplo 2), o que representa o ascenso lento da catedral por riba da auga. Cando escoitamos a pasaxe do compás 18, recoñecemos a súa relación coa pasaxe do c. 1 porque regresa o mesmo conxunto de intervalos ordenados, só que comezando nunha altura diferente. A transposición mantén o contido interválico e, alén diso, tamén mantén a disposición específica de intervalos.
Exemplo 2. Transposición dun motivo, ordenado e non ordenado.
Este mesmo motivo mantense dunha maneira menos evidente ao pasar do c. 18 ao c. 19 (en vermello no Exemplo 2). Aquí, o conxunto de clases de altura non ordenado está trasposto, mais non o conxunto ordenado de antes. Pode que isto non pareza unha transposición tan obvia como a do outro motivo, pero secolocamos as alturas na orde normal, a relación interválica da transposición xa se torna clara.
É frecuente que a transposición se abrevie como Tn, onde n, p número índice dunha transformación, representa o intervalo de clases de altura ordenado que hai entre os dous conxuntos. A transposición é unha operación, algo que se lle fai a unha altura, clase de altura ou colección destas. A transposición tamén pode servir de medida, pois representa a distancia entre dúas cousas.
Transposición dun conxunto
Para traspormos un conxunto mediante Tn, sumamos n a cada número enteiro do conxunto (mod 12, que significa que os números recomezan ao chegar ao 12, como nun reloxo).
Se tomamos a colección de clases de altura do compás 1 de antes e aplicamos unha transposición T4:
[11, 2, 4] – 4 4 4 = [3, 6, 8]
O resultado son as clases de altura do c. 18.
T4 [11, 2, 4] = [3, 6, 8]
Identificación de transposicións e cálculo do número índice
Para determinarmos a relación de transposición entre dous conxuntos, subtraemos o primeiro conxunto do segundo. Se os números resultantes son todos iguais, os dous conxuntos están relacionados por esa Tn. Por exemplo, para clasificar as frechas do Exemplo 1, un analista subtraería os números enteiros das clases de altura do c. 1 aos números enteiros das clases de altura do c. 18. Repara en que os dous conxuntos deberían estar en orde normal.
[3, 6, 8] – [11, 2, 4] = 4 4 4
[3, 6, 8] e [11, 2, 4] están relacionados por T4.
Inversión
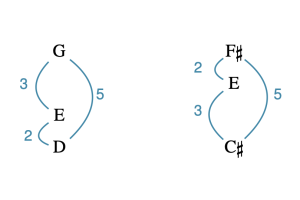
A inversión, como a transposición, adoita asociarse co movemento que conecta obxectos semellantes. A pasaxe do Exemplo 3 da obra Duo Ye (2000), de Chen Yi é bo exemplo: igual que acontecía nas pasaxes relacionadas por transposición, estes dous xestos teñen o mesmo contido interválico, de modo que o noso oído os recoñece como moi similares. Porén, ao contrario da transposición, o contido interválico dos dous xestos non está disposto da mesma maneira: os dous teñen os mesmos intervalos, mais o conxunto [1, 4, 6] ten o intervalo 3 no inicio en vez de no final (Exemplo 4).
Exemplo 3. [2, 4, 7] is inverted to become [1, 4, 6].
Inversión xeral
Se tes que inverter un conxunto e non sabes o número índice, deberás asumir que invertes o conxunto mod 12. Isto significa que tomas o complemento de cada número mod 12. O complemento de cada número enteiro x mod 12 é o número y que resulta da diferenza entre x e 12. Por exemplo, o complemento de 4 é 8: 4+8=12. O complemento de 6 é 6: 6+6=12. O complemento de 0 é 0: 0+0=0, que é 12 mod 12.
Inverter [2, 4, 7] deste xeito daría [5, 8, 10].
In: Método de inversión+transposición
Ás veces, os conxuntos son invertidos e traspostos, como no Exemplo 3. A abreviatura disto é In.
No Exemplo 3, o primeiro conxunto [2, 4, 7] está invertido mediante I8. Para inverter mediante I8, podes seguir este proceso, nesta orde:
- Inversión: [2, 4, 7] tórnase [5, 8, 10].
- Transposición: se sumamos 8 a cada número de [5, 8, 10] obtemos [1, 4, 6].
In: Método da subtracción
Podes calcular o novo conxunto que crea In subtraendo todas as clases de altura do teu primeiro conxunto a n.
Cal é a I8 de [2, 4, 7]?
8 8 8 – [2, 4, 7] = [6, 4, 1]
I8 [2, 4, 7] = [1, 4, 6].
Identificación de inversións e números índice
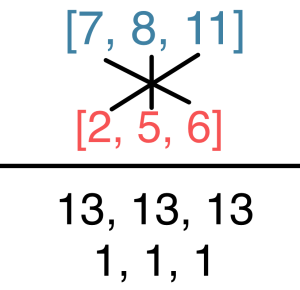
Calquera par de alturas que estea relacionado por inversión pode sumarse para formar o número índice. Isto ten sentido como extensión lóxica do método de subtracción que describimos antes: se a altura invertida y é o resultado de n–x, entón tamén é verdade que n = x + y.
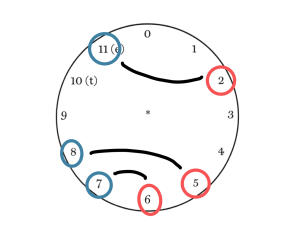
Tamén o podes visualizar nun reloxo. Se tes dous conxuntos e ambos están 1) na orde normal e 2) relacionados por inversión, as notas de cada conxunto estarán en fronte na orde inversa, como mostra o Exemplo 5. Escribe os dous sets, un enriba do outro, na forma normal, despois suma os números enteiros opostos de cada conxunto como se demostra no Exemplo 6 para obter o número índice da relación I. Se a suma de cada par de números é 12 ou máis, subtrae 12 para o que teu n estea en mod 12.
Como usar o reloxo para traspor e inverter
Se prefires un método máis visual para traspor e inverter, podes ver o vídeo do Exemplo 7 (en inglés).
https://coursemedia.gmu.edu/embed/secure/iframe/entryId/1_wuclkc6h/uiConfId/+44431031/st/0
Exemplo 7. Using the clock face for transposition and inversion of pitch class sets.
- Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. Upper Saddle River, NJ: Prentice Hall.
- Blank clock faces (integer notation)
- Blank clock faces (letter names)
- Set Theory Quick Reference Sheet: summarizes the definitions of pitch vs. pitch class, intervals vs. interval classes, and sets vs. set classes.
- Worksheet on normal form and transformations (.pdf, .docx). Asks students to calculate normal form of various sets, and to calculate Tn/In relationships in “Nacht” by Arnold Schoenberg.
- Composition prep worksheet (.pdf, .docx). Prepares students for the set class composition by asking them to find sets and transformations.
Media Attributions
- inversion-2
- Inversional pairs
- Cross-addition for inversion
A group of pitch classes.
A group of pitches that are octave equivalent and enharmonically equivalent.
The most compressed way to write a given collection of pitch classes.
An integer x's complement mod 12 is the number y that would sum to 12. For example, 11's complement mod 12 is 1.
Ordering the notes of a chord so that it is entirely stacked in thirds. The root of the chord is on the bottom.
A group of things that appear in a specified sequence. An ordered pitch set, for example, appears in a consistent order within a piece of music. Compare against a pitch class set, where the pitches are unordered, meaning they can appear in any order in the piece of music.
In a transformation (Tₙ or Iₙ), n is the index number, representing the interval of transposition in semitones.
Short for modulo 12, where numbers wrap around upon reaching 12. Arithmetic in mod 12 is most commonly encountered in clock time: after 12 o’clock, the time becomes 1 o’clock again.