2

La longueur d’onde, typiquement identifiée par le symbole grec lambda (λ) et mesurée en centimètres ou en mètres, est la distance d’un cycle complet ou d’une oscillation d’un signal AC. Le courant alternatif change continuellement entre la tension positive et négative. Une oscillation ou cycle de ce courant alternatif est défini comme un changement du haut vers le bas, puis vers le haut, ou de positif vers négatif, puis vers positif. La longueur d’onde est la distance entre deux crêtes successives ou deux vallées successives. On peut dire également que c’est la distance qu’un seul cycle du signal RF parcourt.

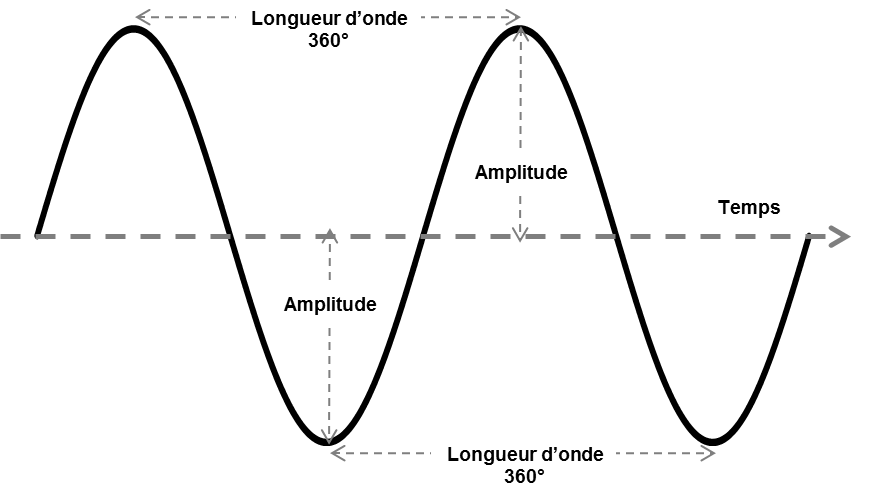
Il est important de comprendre qu’il existe une relation inverse entre la longueur d’onde et la fréquence. Une onde a une certaine vitesse, fréquence et longueur, unies par la relation suivante pour qualifier la vitesse en mètres/secondes, avec la fréquence en cycles/seconde (ou Hertz, abrégé Hz) :

[latex]Vitesse=Fr\acute{e}quence \times Longueur\,Onde[/latex]

Dans le cas d’ondes électromagnétiques la vitesse est celle de la lumière ([latex]299.792.458 \frac{m}{s})[/latex], notée [latex]c = 3.108 m.s^{-1}[/latex] ou [latex]3.108 \frac{m}{s}[/latex] en valeur arrondie. La lumière est une onde électromagnétique et la Célérité (du latin celeritas voulant dire vitesse) de la lumière est le vocable utilisé pour la vitesse de propagation d’une onde. La formule peut alors s’écrire :

[latex]c=f \times \lambda[/latex]

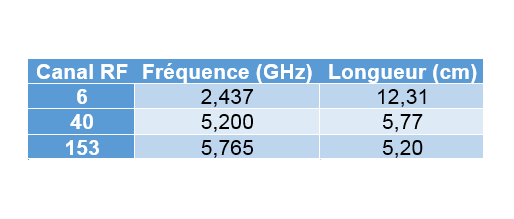
En prenant, comme exemple, le canal 6 (2,437 GHz, c’est à dire 2.437.000.000 cycles/seconde) de la bande des 2,4 GHz, la formule devient :

[latex]\lambda=\frac{c}{f}=\frac{299792458}{2437000000}\text{\ensuremath{\approx}}0,1231\,m\text{\ensuremath{\approx}}12,31\,cm[/latex]

Une méthode rapide pour mémoriser la formule consiste à se rappeler que : [latex]\lambda_{(cm)}=\frac{30}{f_{(GHz)}}[/latex]

La distance qu’une onde peut parcourir dépend du rapport entre la longueur de l’onde et la taille des obstacles qui se trouvent sur son chemin de propagation. Les vagues de longueur d’ondes élevée (plus basse fréquence) ont tendance à pénétrer les objets mieux que les ondes a plus courte longueur d’onde (plus haute fréquence). Plus rapide est l’oscillation ou cycle d’une onde, plus d’information celle-ci pourra transporter car chaque oscillation ou cycle peut, par exemple, être utilisé pour transporter un bit numérique, un ‘0 ‘ou un ‘1’, un «oui» ou un «non».

Quand les signaux RF traversent l’espace et la matière, il perdent de la force (atténuation). On pense souvent qu’un signal de plus haute fréquence avec une plus petite longueur d’onde va subir une atténuation plus rapide qu’une fréquence plus basse avec une longueur d’onde plus large. En réalité, les propriétés de fréquence et de longueur d’onde d’un signal RF ne causent pas l’atténuation. La distance est la principale cause de l’atténuation. Toutes les antennes possèdent une zone d’efficacité, appelée ouverture, pour recevoir l’énergie. La quantité d’énergie qui peut être capturée par l’ouverture d’une antenne est plus petite avec les antennes de plus hautes fréquences. Théoriquement, les signaux électromagnétiques voyagent sans fin dans le vide. Cependant, quand les signaux voyagent au travers de notre atmosphère, ils vont s’atténuer à des amplitudes en deçà du seuil de sensibilité de réception de la radio réceptrice. Le signal arrive au récepteur mais il est trop faible pour être détecté.

Une bonne analogie pour imager ce phénomène, consiste à considérer une voiture qui descend une rue avec de la musique forte. On entendra les basses de la musique (plus basses fréquences) avant d’entendre la voiture.

Les signaux de plus hautes fréquences s’atténueront plus vite, en traversant des structures, que les signaux de plus basses fréquences. Il est important de comprendre pourquoi. Premièrement, la distance couverte est dépendante de l’atténuation dans l’air (connue sous le nom « Free Space Loss »). Deuxièmement, plus la fréquence est haute et moins le signal va pénétrer les obstacles (par exemple, les signaux des stations AM portent plus loin que les signaux des stations FM).