8
L'unité de base de la mesure RF est le watt. Un point d'accès peut être réglé à 30 mW (milliwatts) par exemple. D'autres unités de mesure sont le dB, dBi, dBd et dBm. Les unités de mesure qui sont utilisées pour mesurer l'amplitude émise et reçue sont des mesures de puissance absolues. Les unités de mesures relatives sont souvent utilisées pour établir le gain ou la perte lié à l'introduction d'un câble ou d'une antenne. Les mesures relatives sont aussi utilisées pour représenter la différence de puissance entre un point A et un point B. En d'autres termes, les unités relatives sont des mesures de changement de puissance.

Watt
Un watt (W) est l'unité principale de mesure de puissance, du nom de l'inventeur écossais du 18ème siècle James Watt.. La quantité de puissance émise par une borne est un exemple de mesure absolue de puissance. C'est la vraie mesure de puissance et non pas un ratio ou une valeur relative. En d'autres termes, c'est une quantité de puissance mesurable avec un instrument adapté comme un wattmètre. Une mesure de puissance maximum typique rencontrée dans le domaine du Wi-Fi correspond à 100 mW.
La mesure de puissance AC peut être calculée à l'aide de la formule : [latex]P=E \times I[/latex] avec [latex]P[/latex] en tant que puissance en watt, E en tant que tension en volt et I en tant qu'intensité en ampère. Un watt est égal à un ampère (amp) de courant circulant à un volt.
Milliwatt
Un milliwatt correspond à [latex]\frac{1}{1000}[/latex] de watt. L'intérêt de cette unité de mesure est que la majorité des équipements 802.11 d'intérieur transmettent à des niveaux de puissance compris entre 1 mW et 100 mW. Il faut prendre en compte le fait que les câbles vont atténuer le signal et que l'antenne va l'amplifier. Bien que les organismes de régulation, tels que le FCC, peuvent permettre une puissance en sortie, "Intentional Radiator" (IR), allant jusqu'à 1 watt, seuls quelques rares cas d'utilisation de ponts en point-à-point, nous amènent à utiliser des équipements 802.11 avec plus de 300 mW de puissance de transmission.
Tous les constructeurs ne représentent pas les puissances de transmission de la même manière. les réglages de puissance de transmission de la majorité des constructeurs représente l'IR, alors que que les valeurs d'autres constructeurs représentent l'EIRP. Certains mettront les valeurs en mW alors que d'autres utiliseront le dBm ou même un pourcentage.
Décibel
Le décibel est une unité de comparaison et non une unité de mesure. Par conséquent, il est utilisé pour représenter une différence entre deux valeurs. Le décibel est une expression relative et une mesure de changement de puissance. Dans les réseaux sans fil, les décibels sont souvent utilisés, soit pour comparer la puissance de deux émetteurs, soit plus généralement, pour comparer la différence ou perte entre l'EIRP à la sortie de l'antenne émettrice et la quantité de puissance reçue par l'antenne du récepteur.
Le décibel est dérivé du terme bel. Les employés de "Bell Telephone Laboratories" avaient besoin d'une manière de représenter les pertes de puissances, en tant que ratios de puissances, sur les lignes téléphoniques. Ils ont défini le bel comme un ratio de 10 pour 1 entre la puissance de deux sons. Prenons par exemple un point d'accès qui transmet à 100 mW. Le portable1 reçoit le signal de la borne à un niveau de puissance de 10 mW et le portable2 reçoit le signal de la borne à un niveau de puissance de 1 mW. La différence entre le signal de la borne (100 mW) et le portable1 (10 mW) est de 100:10, soit un ratio de 10:1 ou 1 bel. La différence entre le signal du portable1 (10 mW) et du portable2 (1 mW) est aussi un ratio de 10:1, soit 1 bel. Donc la différence de puissance entre le point d'accès et portable2 est de 2 bels.
Les bels peuvent être étudiés sous un angle mathématique à l'aide des logarithmes. Appelons [latex]P_{AP}[/latex] la puissance du point d'accès et [latex]P_{p2}[/latex] la puissance du portable2. La formule est [latex]y=log(P_{AP}/P_{P2})[/latex], soit [latex]y=log(100/1)[/latex] ou [latex]y=log(100)[/latex]. La question devient : à quelle puissance doit on élever 10 pour obtenir 100 ? La réponse est 2 bels car [latex]10^{2}=100[/latex].
Dans certains environnements les bels ne sont pas assez précis et c'est pour cela que l'on utilise les décibels à la place. Un décibel est égal à [latex]1/10[/latex] de bel, donc pour calculer les décibels il faut multiplier les bels par 10.
[latex]bels=log(P_{1}/P_{2})[/latex]
[latex]d\acute{e}cibels=10 \times log(P_{1}/P_{2})[/latex]
En reprenant l'exemple précédant afin de calculer en décibels, la formule devient : [latex]y=10 \times log(100/1)[/latex] ou [latex]y=10 \times log(100)[/latex], c'est à dire +20 décibels ou +2 bels.
Il est possible de travailler avec les milliwatts, mais dans la mesure où les changement de puissances se calculent avec des formules logarithmiques, les différences entre les valeurs peuvent devenir très grandes et difficiles à manipuler. Il est plus simple de dire qu'un signal de 100 mW décroit de 70 dB plutôt que de dire qu'il s'est atténué à 0,00001 mW. C'est pour cette raison que la formule de "Free Space Path Loss" (FSPL) est donnée sous forme logarithmique.
Décibel isotrope
De manière théorique, une antenne isotrope peut diffuser un signal équivalent dans toutes les directions. Il est impossible de construire une antenne capable de faire ça. Dans certains cas, on ne souhaite pas diffuser dans toutes les directions parce qu'on préfère concentrer le signal de l'antenne dans une direction particulière. Le gain de puissance d'une antenne comparé à ce qu'une antenne isotrope générerait s'appelle "Decibels Isotropic" (dBi) ou gain en décibel par rapport à une antenne isotrope ou changement de puissance par rapport à une antenne. Du fait que les antennes sont mesurées en gain et non pas en puissance, on peut en conclure que le dBi est une mesure relative et non une mesure absolue. le dBi est le gain de l'antenne mesuré au point le plus fort ou point de concentration du signal de l'antenne. Dans la mesure où les antennes concentrent toujours leur énergie plus dans une direction qu'une autre, la valeur dBi d'une antenne est toujours un gain positif et non une perte. Il existe, tout de même, des antennes avec des valeur dBi à 0, qui sont appelées des antennes "No-gain" ou "Unity-gain".
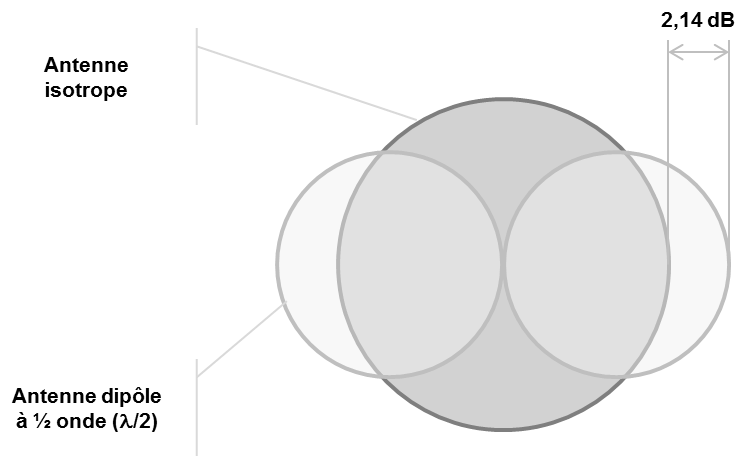
L'antenne dipôle "Half -wave" est un type d'antenne classique utilisée sur les points d'accès. C'est une petite antenne omnidirectionnelle, d'usage général, recouverte de caoutchouc. Une antenne dipôle demi-onde 2,4 GHz possède une valeur dBi de 2,14.
Décibel dipôle
Si la puissance en entrée d'une antenne est de 100 mW et que la puissance à la sortie est de 200 mW, le gain de l'antenne est de 3 décibel istrope (dBi). Le gain de certaines antennes peut être mesuré en décibel dipôle (dBd) ou gain en décibel par rapport à une antenne dipôle. Une antenne dipôle est omnidirectionnelle. L'unité dBd est est une mesure relative et non une mesure de puissante. Une antenne dipôle standard a une valeur dBi de 2,14. Si une antenne a une valeur de 3 dBd, cela signifie qu'elle est 3 dB supérieure a une antenne dipôle. Dans la mesure où une antenne dipôle a une valeur de 2,24 dBi, il suffit d'ajouter 3 à 2,14 pour déterminer que cette antenne est équivalente à une antenne de 5,14 dBi.
[latex]0\,dBd=2,14\,dBi[/latex]
[latex]dBi=dBd+2,14[/latex]
[latex]dBd=dBi-2,14[/latex]
Décibel milliwatt
La mesure de l'énergie RF en mW n'est pas toujours adéquate pour travailler avec des petites valeurs. Le dBm ("db"-milliwatts) est la comparaison du niveau de puissance comparé à un milliwatt (0 dBm = 1 mW et +20 dBm = 100 mW). Du fait que le dBm est une mesure relative (dB) qui est comparée à une valeur absolue connue (1 mW), c'est une mesure absolue et logarithmique de puissance du signal. Étant donné que dans le monde du Wi-Fi, les valeurs de puissance manipulées sont très faibles (< 1 mW), les valeurs en milliwatts sont converties en logarithme de base 10. Comme les valeurs obtenues en logarithmes sont assez faibles, alors la convention multiplie cette valeur par 10 pour obtenir une unité appelée dBm.
[latex]P_{dBm}=10 \times log(P_{mW})[/latex]
et
[latex]P_{mW}=10^{\frac{P_{dBm}}{10}}[/latex]
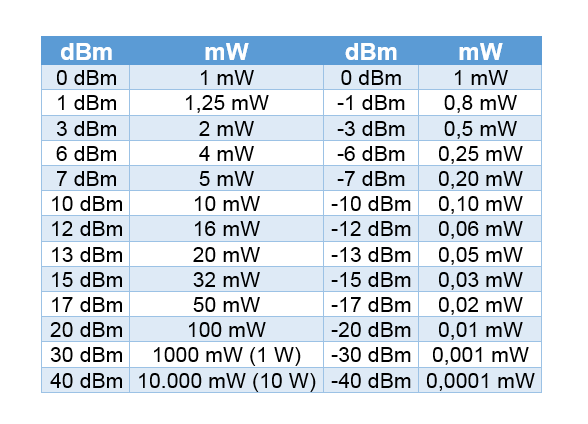
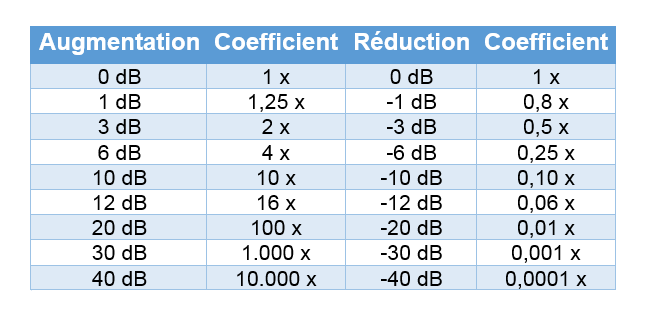
On observe, dans le tableau ci-dessus que :
- 0 dBm équivaut à 1 mW
- une augmentation de 3 dB correspond au doublement (2x) de la puissance
- une augmentation de 6 dB équivaut au quadruplement (4x) de la puissance
- une augmentation de 10 dB équivaut à multiplier la puissance par 10
- une baisse de 3 dB implique une réduction de moitié ([latex]\frac{1}{2}x[/latex]) de la puissance
- une baisse de 6 dB correspond à une réduction du quart ([latex]\frac{1}{4}x[/latex]) de la puissance
- une baisse de 10 dB équivaut diviser la puissance par 10
Comparons les deux formules FSPL suivantes pour calculer la perte pour un signal en 2,4 GHz dont la source est à 100 mètres (0,1 km), puis à 200 mètres (0,2 km) :
[latex]FSPL=32,4+(20 \times log(2.400)+20 \times log(0,1))=80,00422\:dB[/latex]
[latex]FSPL=32,4+(20 \times log(2.400)+20 \times log(0,2))=86,02482\:dB[/latex]
On constate qu'en doublant la distance, le signal reçu décroit de 6 dB. Quels que soient les nombres choisis, si la distance est doublée, la perte en décibels est de 6 dB. Cette règle implique aussi que si on augmente l'amplitude de 6 dB, la distance utile est doublée. La règle des 6 dB est très utile pour comparer la taille des cellules ou pour estimer la couverture d'un émetteur. Cette règle est également utile pour comprendre le gain d'une antenne, car tous les 6 dB de gain d'antenne supplémentaire, on double la distance du signal RF utilisable. De même, tous les 6 dB de perte, on divise par deux la distance utile.
La conversion en dBm facilite également les calculs. Si un émetteur génère un signal de +20 dBm et que l'antenne ajoute un gain de 5 dBi au signal, alors la puissance diffusée en sortie d'antenne (EIRP) est égale à la somme des deux nombres : +25 dBm.
Loi en carré inverse
En réalité, la règle des 6 dB est basée sur la loi en carré inverse ou "Inverse Square Law", développée à l'origine par Isaac Newton. La puissance du signal ne diminue pas de manière linéaire, mais en fonction de l’inverse du carré de la distance.
[latex]P=\frac{PIRE}{4 \times \pi \times D^{2}}=\frac{1}{4 \times \pi} \times \frac{PIRE}{D^{2}}=0,0795 \times \frac{PIRE}{D^{2}}[/latex]
Avec :
- PIRE = Puissance Isotrope Rayonnée Équivalente ou "Equivalent Isotropic Radiated Power" (EIRP)
Cela signifie que si on reçoit un signal à un certain niveau de puissance et à une certaine distance ([latex]D=1[/latex]) et que l'on double cette distance ([latex]D=2[/latex]), alors le nouveau niveau de puissance sera de [latex]\frac{1}{2^{2}}[/latex] ou [latex]\frac{1}{4}[/latex] de celui d'origine.
Pour information, la formule de Friis utilisée pour le calcul de "Free Space Path Loss" (FSPL) est également basée sur la loi en carré inverse de Newton.
Astuces de calcul
Il est possible de manipuler les mathématiques RF sans utiliser les logarithmes, afin de trouver des valeurs approchées. Nous connaissons déjà la règle des 6 dB, qui indique que pour doubler la distance utile, la puissance du signal doit être augmentée de 6 dB, ce qui revient à multiplier la puissance absolue émise par 4 (2 x 3 dB).
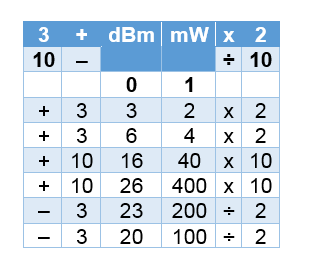
La règle des 10 et des 3 comporte quatre composantes à retenir :
- Pour chaque gain de 3 dB (relatif), on double la puissance absolue (mW)
- Pour chaque perte de 3 dB (relatif), on divise par deux la puissance absolue (mW)
- Pour chaque gain de 10 dB (relatif), on multiplie par 10 la puissance absolue (mW)
- Pour chaque perte de 10 dB (relatif), on divise par 10 la puissance absolue (mW)
Par exemple, si le point d'accès est configuré pour émettre à 100 mW est que l'antenne fournit un gain passif de 3 dBi, alors la quantité d'énergie diffusée par l'antenne (EIRP) est de 200 mW. Si le point d'accès est connecté à un câble qui introduit une perte de 3 dB, alors le niveau d'amplitude absolue à la sortie du câble est de 50 mW.
Il faut garder à l'esprit que le dBm est une unité de puissance et que le dB est une unité de changement qui peut être appliquée à dBm. Si on part d'un signal de +10 dBm et que l'on applique une augmentation de 3 dB, on ajoute ces deux nombres pour obtenir un signal de + 13 dBm.