Learning Objectives
In this section, you will:
7.2.1 – Use right triangles to evaluate trigonometric functions.
7.2.2 – Use the definitions of trigonometric functions of any angle.
7.2.3 – Use right-triangle trigonometry to solve applied problems.
Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.
7.2.1 – Using Right Triangles to Evaluate Trigonometric Functions
(Figure) shows a right triangle with a vertical side of length [latex]\,y\,[/latex] and a horizontal side has length [latex]\,x.\,[/latex] Notice that the triangle is inscribed in a circle of radius 1. Such a circle, with a center at the origin and a radius of 1, is known as a unit circle.
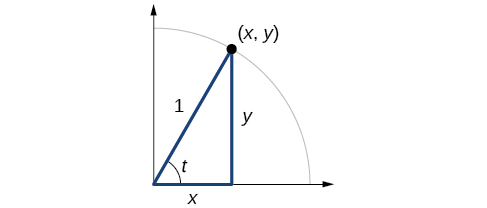
We can define the trigonometric functions in terms an angle t and the lengths of the sides of the triangle. The adjacent side is the side closest to the angle, x. (Adjacent means “next to.”) The opposite side is the side across from the angle, y. The hypotenuse is the side of the triangle opposite the right angle, 1. These sides are labeled in (Figure).

Given a right triangle with an acute angle of [latex]\,t,[/latex] the first three trigonometric functions are listed.
A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.”
For the triangle shown in (Figure), we have the following.
How To
Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle.
- Find the sine as the ratio of the opposite side to the hypotenuse.
- Find the cosine as the ratio of the adjacent side to the hypotenuse.
- Find the tangent as the ratio of the opposite side to the adjacent side.
Example 1 – Evaluating a Trigonometric Function of a Right Triangle
Given the triangle shown in (Figure), find the value of [latex]\,\mathrm{cos}\,\alpha .[/latex]
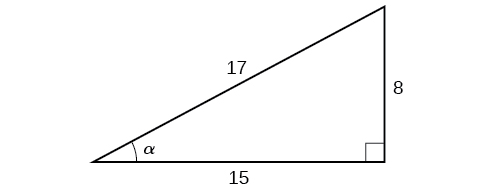
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17.
Try It
Given the triangle shown in (Figure), find the value of [latex]\,\text{sin}\,t.[/latex]
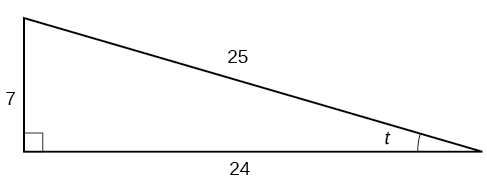
Show answer
[latex]$$\frac{7}{25}$$[/latex]
7.2.2 – Using Trigonometric Functions
In previous example, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.
How To
Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides.
- For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
- Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
- Using the value of the trigonometric function and the known side length, solve for the missing side length.
Example 2 – Finding Missing Side Lengths Using Trigonometric Ratios
Find the unknown sides of the triangle in (Figure).
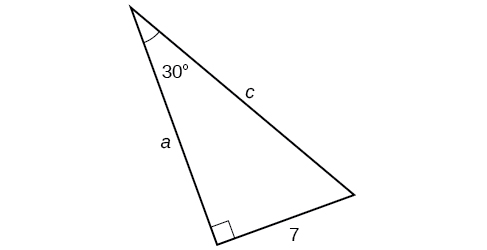
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.
We rearrange to solve for [latex]\,a.[/latex]
We can use the sine to find the hypotenuse.
Again, we rearrange to solve for [latex]\,c.[/latex]
Try It
A right triangle has one angle of [latex]\,\frac{\pi }{3}\,[/latex] and a hypotenuse of 20. Find the unknown sides and angle of the triangle.
Show answer
[latex]\text{adjacent}=10;\text{opposite}=10\sqrt{3};[/latex] missing angle is [latex]\,\frac{\pi }{6}[/latex]
7.2.3 – Using Right Triangle Trigonometry to Solve Applied Problems
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height.
Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye. See (Figure).
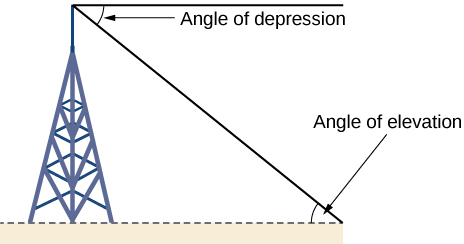
How To
Given a tall object, measure its height indirectly.
- Make a sketch of the problem situation to keep track of known and unknown information.
- Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
- At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
- Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
- Solve the equation for the unknown height.
Example 3 – Measuring a Distance Indirectly
To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of [latex]\,57°\,[/latex] between a line of sight to the top of the tree and the ground, as shown in (Figure). Find the height of the tree.
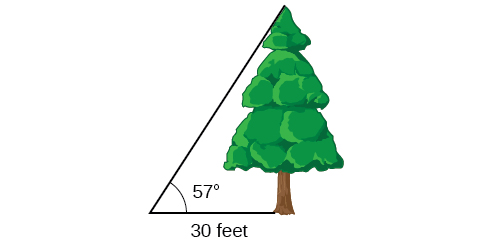
We know that the angle of elevation is [latex]\,57°\,[/latex] and the adjacent side is 30 ft long. The opposite side is the unknown height.
The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of [latex]\,57°,[/latex] letting [latex]\,h\,[/latex] be the unknown height.
The tree is approximately 46 feet tall.
Try It
How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of [latex]\,\frac{5\pi }{12}\,[/latex] with the ground? Round to the nearest foot.
Show answer
About 52 ft
Access these online resources for additional instruction and practice with right triangle trigonometry.
Key Equations
| Trigonometric Functions | [latex]\begin{array}{cc}\text{Sine}\hfill & \phantom{\rule{1em}{0ex}}\text{sin }t=\frac{\text{opposite}}{\text{hypotenuse}}\hfill \\ \text{Cosine}\hfill & \phantom{\rule{1em}{0ex}}\text{cos }t=\frac{\text{adjacent}}{\text{hypotenuse}}\hfill \\ \text{Tangent}\hfill & \phantom{\rule{1em}{0ex}}\text{tan }t=\frac{\text{opposite}}{\text{adjacent}}\hfill \\ \text{Secant}\hfill & \phantom{\rule{1em}{0ex}}\text{sec }t=\frac{\text{hypotenuse}}{\text{adjacent}}\hfill \\ \text{Cosecant}\hfill & \phantom{\rule{1em}{0ex}}\text{csc }t=\frac{\text{hypotenuse}}{\text{opposite}}\hfill \\ \text{Cotangent}\hfill & \phantom{\rule{1em}{0ex}}\text{cot }t=\frac{\text{adjacent}}{\text{opposite}}\hfill \end{array}[/latex] |
| Reciprocal Trigonometric Functions | [latex]\begin{array}{cc}\text{sin }t=\frac{1}{\text{csc }t}\hfill & \phantom{\rule{1em}{0ex}}\text{csc }t=\frac{1}{\text{sin }t}\hfill \\ \text{cos }t=\frac{1}{\text{sec }t}\hfill & \phantom{\rule{1em}{0ex}}\text{sec }t=\frac{1}{\text{cos }t}\hfill \\ \text{tan }t=\frac{1}{\text{cot }t}\hfill & \phantom{\rule{1em}{0ex}}\text{cot }t=\frac{1}{\text{tan }t}\hfill \end{array}[/latex] |
| Cofunction Identities | [latex]\begin{array}{c}\text{cos }t=\mathrm{sin}\left(\frac{\pi }{2}-t\right)\hfill \\ \text{sin }t=\mathrm{cos}\left(\frac{\pi }{2}-t\right)\hfill \\ \text{tan }t=\mathrm{cot}\left(\frac{\pi }{2}-t\right)\hfill \\ \text{cot }t=\mathrm{tan}\left(\frac{\pi }{2}-t\right)\hfill \\ \text{sec }t=\mathrm{csc}\left(\frac{\pi }{2}-t\right)\hfill \end{array}[/latex] |
Key Concepts
- We can define trigonometric functions as ratios of the side lengths of a right triangle. See Example 1.
- We can use trigonometric functions of an angle to find unknown side lengths.
- Select the trigonometric function representing the ratio of the unknown side to the known side. See Example 2.
- Right-triangle trigonometry facilitates the measurement of inaccessible heights and distances.
- The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known. See Example 3.
Glossary
- adjacent side
- in a right triangle, the side between a given angle and the right angle
- angle of depression
- the angle between the horizontal and the line from the object to the observer’s eye, assuming the object is positioned lower than the observer
- angle of elevation
- the angle between the horizontal and the line from the object to the observer’s eye, assuming the object is positioned higher than the observer
- opposite side
- in a right triangle, the side most distant from a given angle
- hypotenuse
- the side of a right triangle opposite the right angle
- unit circle
- a circle with a center at [latex]\,\left(0,0\right)\,[/latex] and radius 1
