A finais do século XIX, as composicións empregaban con frecuencia progresións triádicas que escapan á análise convencional con números romanos. Observa o seguinte fragmento do concerto para violín e violoncello de Brahms (Exemplo 1):

O Exemplo 2 contén unha redución do fragmento. A pasaxe conecta dúas tríades de La♭ maior, mais os acordes que hai entre esas tríades non pertencen a La♭ maior de ningún modo, nin tampouco seguen as convencións da harmonía funcional.

Poderiamos catalogala simplemente como “harmonía non funcional”, mais ao escoitala si que vemos que segue unha certa lóxica. en palabras de Richard Cohn, “se esta música [que é triádica e ten función indeterminada] non é de todo coherente cos principios da tonalidade diatónica, que outros principios segue?” (1998, 169).

Transformacións neoriemannianas

A teoría neoriemanniana describe unha forma de conectar tríades maiores e menores sen que exista un contexto tonal. O Exemplo 3 mostra as tres operacións neoriemannianas básicas. Repara en que cada operación mantén dúas notas comúns entre as tríades e muda o modo.

• A transformación Relativa (R) mantén a terceira maior da tríade e move a nota restante un ton.
• A transformación Paralela (P) mantén a quinta xusta da tríade e move a nota restante un semitón.
• A transformación por intercambio de sensible (L) mantén a terceira menor da tríade e move a nota restante un semitón. O L do nome provén do alemán leittonwechsel e o inglés leading tone exchange.

É importante salientr que cada transformación é unha alternancia entre dous acordes. Unha boa analoxía é pensarmos na tecla de bloqueo de maiúsculas do teclado do computador, que alterna entre os dous tamaños de letra. Se estás escribindo letras minúsculas e despois premes o bloqueo de maiúsculas, o teclado comeza a escribir en letras maiúsculas, mais se volves premer o bloqueo de maiúsculas, volve ás minúsculas, non vai para unha terceira opción.

Do mesmo xeito, se realizas unha transformación L nunha tríade de Dó maior, obtés unha tríade de Mi menor. Se realizas a atrnasformación L nunha tríade de Mi menor, regresas á tríade de Dó maior. Dito doutra forma, as repeticións sucesivas da mesma transformación alternan entre dous acordes, como no Exemplo 4.

Aínda que a maioría de composicións do século XIX non conteñen progresións que empreguen a mesma transformación de xeito continuado, podes encontrar esta técnicaen obras do século XX, como O Superman de Laurie Anderson, que emprega transformacións  L sucesivas de modo constante.

A Tonnetz

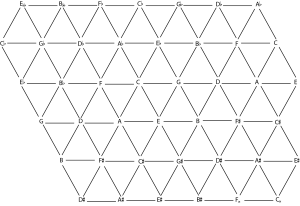
O Exemplo 5 mostra a Tonnetz. Unha Tonnetz (“rede de notas”) é unha representación visual de alturas colocadas de tal forma que as quintas xustas se len de esquerda a dereita, as terceiras maiores se len diagonalmente do recanto superior esquerdo ao inferior dereito e as terceiras menores se len do recanto inferior esquerdo ao superior dereito. Calquera conxunto de tres alturas que forme un triángulo configura unha tríade maior ou menor. As transformacións neoriemannianas poden ser visualizadas como o xiro dun triángulo que utiliza como eixe un dos seus lados.

• A transformación (P)aralela vira o triángulo polo lado que pertence á liña das quintas xustas (esquerda a dereita).
• A transformación (R)elativa vira o triángulo polo lado que pertence á liña de terceiras maiores (de arriba á esquerda a abaixo á dereita).
• The (L)eading-tone transformation vira o triángulo polo lado que pertence á liña das terceiras menores (de arriba á dereita a abaixo á esquerda).

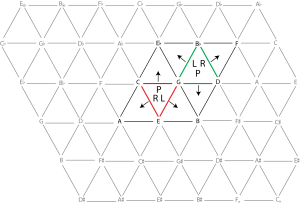
O Exemplo 6 mostra cada unha das transformacións da Tonnetz. Se realizas unha transformación P na tríade maior de Dó, destacada con liñas vermellas, virará polo lado Dó–Sol e tornarase en Dó menor. Do mesmo xeito, L vira a tríade polo lado de Sol-Mi e tórnaa en Mi menor, e R vira a t´riade polo lado Dó-Mi e tórnaa en La menor. Repara en que, se comezas nunha tríade menor, como a tríade de Sol menor que aparece destacada en verde, todos os xiros serán na dirección oposta.
Se volvemos ao exemplo do concerto de Brahms para violín e cello, agora temos unha forma de entender como funciona esta progresión de acordes. O Exemplo 7 demostra que as dúas tríades de La♭ maior están conectadas por unha serie de transformacións P e L entre os acordes.

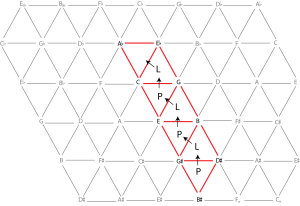
O fragmento deo concerto de Brahms debuxa unha columna de triángulos que se move ascendentemente desde o recanto de abaixo á dereita da Tonnetz, presentado no Exemplo 8. Cómpre mencionar que hai que reinterpretar enharmonicamente a tríade maior de Sol♯ como La♭ major no punto inicial.

A Tonnetz é útil para visualizarmos a proximidade das tríades maior e menor. Repara en que todas as tríades dunha determinada tonalidade están próximos unhas das outras, mentres que as tonalidades máis afastadas tamén están lonxe na Tonnetz. Alén disto, a Tonnetz é útil para imaxinarmos progresións interesantes de acordes que se cadra non se nos ocorrerían se nos limitamos á sintaxe típica da práctica común.

Cadeas ou ciclos de transformacións

Aínda que é posible usarmos a teoría neoriemanniana para crear ou analizar calquera progresión de acordes, as compositoras e compositores adoitan centrarse en cadeas de operacións que crean círculos fechados de tríades. Os ciclos comezan e terminan no mesmo acorde, e seguen un padrón concreto de transformacións (como nunha secuencia). A progresión do exemplo de Brahms é un ciclo PL porque alterna as transformacións P e L, alén de comezar e terminar no mesmo acorde.

Hai tres ciclos posibles que usan dúas transformacións: o ciclio PL, o ciclo RP, e o ciclo RL. Como podes observar no Exemplo 9, os ciclos PL e RP “fechan o círculo” após relativamente poucas transformacións: seis no ciclo PL e oito no ciclo RP.

En contrapartida, o ciclo RL (Exemplo 10) é bastante longo: pasa polas 24 tríades maiores e menores, que son todas as posibles. Dado que este ciclo tarda tanto en “fechar o círculo”, é habitual que sexa ignorado ou presentado en forma truncada.

Hai un ciclo de tres transformacións que é  notorio: o ciclo PLR. Como mostra o Exemplo 11, fan falta dous ciclos de transformacións PLR para regresar ao acorde inicial.

Dos ciclos que mencionamos até agora, tanto o PL como o RP xeran unha escala sumando todas as notas que empregan as tríades que os constitúen. O ciclo PL xera a escala hexatónica, unha escala simétrica que alterna semitóns e terceiras menores. O ciclo RP xera unha escala octatónica, outra escala simétrica, que alterna semitóns e segundas maiores. Poderías considerar estas escalas para representares o “son xeral” do ciclo. Un ciclo PLR está centrado nunha únic altura, que aparece en todas as tríades do ciclo.

Cada un destes ciclos está ilustrado no Exemplo 12.

Outras transformacións

Hai outros tipos de transformacións neoriemannianas que aparecen coa suficiente frecuencia no repertorio como para seren mencionadas aquí.

• A transformación por Slide (S) é, na práctica, o contrario da transformación P: move as dúas alturas que forman a quinta xusta nunha tríade a distancia dun semitón e muda o modo da tríade. A palabra slide é un termo inglés que significa “desprazamento” ou “escorregamento”, mais adoita usarse na lingua orixinal ^[1]
• A transformación por Nebenverwandt (N) move as dúas notas que forman a terceira menor nunha tríade a distancia de semitón e, de novo, muda o modo. Nebenverwandt é un termo alemán que poderiamos traducir como “por proximidade” ou “veciñanza”, e fai referencia ao movemento de bordadura ou nota auxiliar que fai esta terceira. ^[2]
• A transformación por hexapolo ou Hexpole (H) conecta a tríade unha tríade do outro modo que esta a distancia de terceira, movendo cada voz a distancia de semitón. Isto xera dous polos hexatónicos do ciclo PL hexatónico que mencionamos anteriormente e que se mostra no Exemplo 12.^[3]

Estas tres transformacións aparecen no Exemplo 13.

Como é evidente, estas tres transformacións poden ser consideradas como combinacións das transformacións báiscas P, L, e R. Por exemplo, poderiamos describir H como “PLP.” Certamente, é posible describirmos a conexión entre dúas tríades maiores ou menores como combinacións de transformacións: podes ir de calquera tríade a calquera outra en cinco pasos ou menos. As máis interesantes son as conexións que empregan unha condución de voces “parsimoniosa”, que é aquela en que non hai ningunha voz que se mova máis dun ton.  Hai moitas outras combinacións que poderías tentar imaxinar, tenta elaborar algunhas propias!

Máis redes de transformacións neoriemannianas

Tríades aumentadas

Aínda que non formen parte das transformacións neoriemannianas básicas, que só tratan de tríades maiores e menores, a tríade aumentada proporciona unha ligazón útil entre as tríades maiores e as menores, en concreto as que están conectadas por transformacións R. Ao examinares os exemplos anteriores, pode que reparases en que a transformación R non é o mesmo exactamente que unha P ou L, porque move a nota que non se mantén a dous semitóns, mentres que as outras moven as notas que se manteñen só un semitón. De certo modo, a transformación R supón o dobre de “traballo” que as transformacións P e L. Se enchemos o oco que existe entre dúas tríades relacionadas por R, xorde unha tríade aumentada, como se mostra no Exemplo 14.

Isto tórnase máis interesante cando consideramos a ambigüidade da tríade aumentada. Debido a que é un acorde simétrico (como acorde de sétima diminuída), podes reinterpretar enharmonicamente a tríade aumentada de xeito que calquera dos elementos pode facer de fundamental. Por exemplo, a tríade aumentada de Dó do Exemplo 14 tamén se podería escribir como tríade aumentada de Mi (Mi–Sol♯–Si♯), ou tríade aumentada de La♭ (La♭–Dó–Mi). Como resultado, podes resolver a tríade aumentada a tres tríades menores diferentes ao mover só unha voz por semitón, dependendo de como interpretes a fundamental. O Exemplo 15 mostra tres resolucións posiblesda tríade de Dó⁺.

Do mesmo xeito, a mesma tríade aumentada pode conectar con tres tríades aumentadas diferentes ao mover unha soa voz por semitón, como se mostra no Exemplo 16.

O Exemplo 17 ilustra as catro tríades aumentadas (si, só hai catro, debido á simetría do acorde) e as tríades maiores e menores ás que poden resolver se moven só unha voz por semitón. Cada tríade aumentada e as súas seis tríades asociadas forman o que se denomina rexións de Weitzmann, co nome do teórico Carl Friedrich Weitzmann, que escribiu con moito detalle sobre a tríade aumentada e a súa versatilidade en varios tratados do século XIX.
Cada liña dunha rexión de Weitzmann representa o movemento dunha nota da tríade por un só semitón. Cando trazas un camiño desde unha tríade da esquerda até unha da dereita, encontras varias transformacións das que mencionamos anteriormente. Tanto R como S e N requiren un movemento total de dous semitóns, e cada un destes desprazamentos pode ser trazado nunha rexión de Weitzmann.

A Danza do Cubo

Lembra que os ciclos LP, RP, e PLR son “fechados”. Estes padróns recorrentes son interesantes, mais poderían causar monotonía despois dun pouco. E se houbese un xeito de modular entre ciclos? Para iso precisamos unha tríade aumentada.

Revisa de novo as tríades maiores conectadas na rexión Weitzmann de Dó⁺: Dó, Mi, e La♭. Repara en que esas tres tríades maiores son as mesmas que encontramos no ciclo PL que comezaba en Dó, que tes no Exemplo 12. As tríades menores dese ciclo PL pertencen a outra rexión de Weitzmann: a rexión de Mi♭⁺. Se engadimos tríades aumentadas nos nosos ciclos PL, ampliamos o grupo de acordes posibles nun ciclo de seis a oito. En vez de representar estes ciclos nun hexágono, ímolos representar nun cubo, como se ve no Exemplo 18.

O ciclo PL que comeza en Dó está no recanto superior dereito do Exemplo 18. Cada cara do cubo representa o movemento por semitón dunha nota da tríada. Cando as tríades se moven de maior a menor, prodúcense transformacións P ou L. As tríades aumentadas que conectan coas tríades maiores e menores están nos recantos opostos do cubo e, obviamente, tamén conectan con cada tríade adxacente por un semitón.

Entón, como poderiamos “modular” dun ciclo PL para outro? Repara en que esa mesma tríade aumentada está presente en dous cubos diferentes. Se escribísemos unha progresión de acordes dentro dun ciclo PL, poderiamos “saltar” a un ciclo PL adxacente mediante unha desas dúas tríades aumentadas, para despois continuar no novo ciclo. De certo modo, cada cubo está conectado con outros dous cubos mediante unha tríade aumentada. Podemos utilizar estas conexións para crearmos unha soa ilustración que proporciona un mapa de todas as tríades maiores e menores que están conectadas por un só semitón. Esta teoría foi exposta por primeira vez por Jack Douthett e Peter Steinbach (1998), que denominaron este diagrama “danza do cubo” (cube dance). A danza do cubo está reproducida no Exemplo 19.

Ao usarmos o modelo da danza do cubo, poderías crear unha progresión que comece no ciclo PL que inclúe Dó, modular a un novo ciclo PL mediante as tríades C⁺ ou Mi♭⁺. Se quixeses chegar de Dó a Re, por exemplo, terías que modular dúas veces: ben mediante Dó⁺ e Re♭⁺, ou Mi♭⁺ e Re⁺. Aínda que os outros ciclos non están claramente representados no modelo da danza do cubo, tamén podes empregar tríades aumentadas para modular entre ciclos RP ou PLR, así como entre calquera grupo de transformacións neoriemannianas que inclúan transformacións R.

Periamos dicir que a danza do cubo até é máis útil que a Tonnetz para ilustrar a proximidade das tríades maiores e menores. Se equiparamos a proximidade co número total de semitóns que son precisos para movernos dunha tríade a outra, o diagrama da danza do cubo xunta os acordes que considerariamos intuitivamente máis próximos, mentres que os que consideramos distantes están relativamente máis lonxe. Alén disto, a danza do cubo (e mesmo a Tonnetz) fai isto sen referencia a un centro tonal, o que fai que sexa máis útil para racionalizarmos as progresións de acordes daquela música dos séculos XIX, XX (e mesmo XXI) que  é triádica pero distanciada da tonalidade funcional. A súa grande utilidade aflora para analizarmos este tipo de música, ou mesmo para realizar composicións propias.

• Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15, no. 1 (March): 9–40.
• Cohn, Richard. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations.” Journal of Music Theory 41, no. 1 (Spring): 1–66.
• Cohn, Richard. 1998. “Introduction to Neo-Riemannian Theory: A Survey and a Historical Perspective.” Journal of Music Theory 42, no. 2 (Autumn): 167–80.
• Cohn, Richard. 1998. “Square Dances with Cubes.” Journal of Music Theory 42, no. 2 (Autumn): 283–96.
• Cohn, Richard. 2004. “Uncanny Resemblances: Tonal Signification in the Freudian Age.” Journal of the American Musicological Society 57, no. 2 (Summer): 285–323.
• Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42, no. 2 (Autumn): 241–63.
• Engebretsen, Nora, and Per F. Broman. 2007. “Transformational Theory in the Undergraduate Curriculum – A Case for Teaching the Neo-Riemannian Approach.” Journal of Music Theory Pedagogy 21:39–69.
• Mason, Laura Felicity. 2013. “Essential Neo-Riemannian Theory for Today’s Musician.” Master’s thesis, University of Tennessee, Knoxville. https://trace.tennessee.edu/utk_gradthes/1646.

1. Worksheet on Neo-Riemannian Transformations (.pdf, .mscz). Asks students to perform P, L, R, SLIDE, N, and H on individual triads, to realize chains of transformations, and find a transformation chain to connect two chords.
2. Composing with Neo-Riemannian Transformations (.pdf, .mscz). Asks students to use the Cube Dance and other Neo-Riemannian cycles to compose a short minimalist piano solo.