Chapter 2: Homework Solution

7

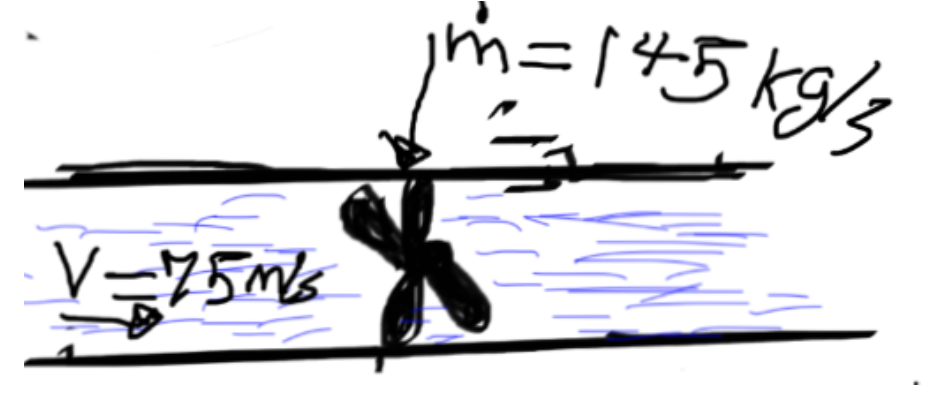
Water moves inside a pipe at 75 m/s with a flow rate of 145 kg/in in order to generate power by moving a propeller located inside the pipe.

$v = 75 \ \si\m/\si\s$
$\dot{m} = 145 \ \si\kg/\si\s$

Given:

Velocity(v)=75m/s

Mass flow rate $(\dot{m})$ =145 kg/s

Find:

Determine the power generation at the propeller.

Solution:

$e_{mech}=ke=\frac{v^2}{2}=\frac{75^2(\frac{m}{s})^2}{2}(\frac{1(\frac{kJ}{kg})}{1000(\frac{m}{s})^2})=2.8125kJ/kg$

$\dot{W}_{max}=\dot{E}_{mech}=\dot{m}e_{mech}$

$\dot{W}_{max}=(120kg/s)(2.8kJ/kg)=406kW \therefore 1 kJ/s = 1kW$

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Thermodynamics Copyright © by Diana Bairaktarova (Adapted from Engineering Thermodynamics - A Graphical Approach by Israel Urieli and Licensed CC BY NC-SA 3.0) is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.