19

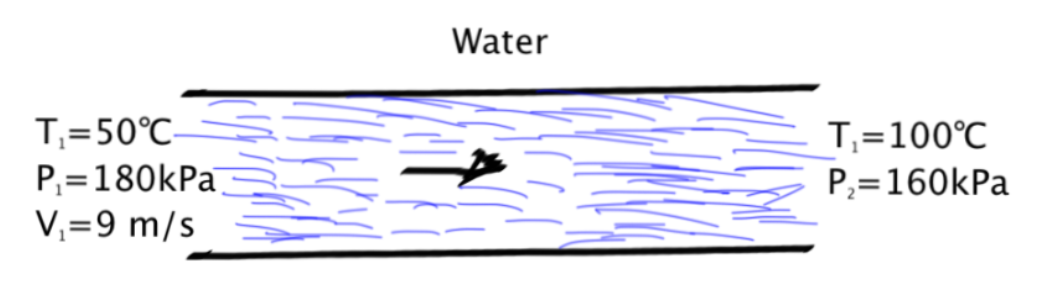
Water is found to move through a pipe at a speed of 9m/s where the temperature of the water at the entrance is found to be 50^{\circ}C, and pressure 180 kPa where the pipe diameter is 0.50m. At the exit the pressure was found 160kPa, and temperature at the 100^{\circ}C. Determine the volume flow rates of water at the inlet and exit, the velocity at the exit, and the mass flow rate.

Screen Shot 2015-08-19 at 2.22.17 PM

T_1=50^\circ\text{C}
P_1 = 180 \ \si\kPa
V_1 = 9 \ \si\m/\si\s
T_1=100^\circ\text{C}
P_2=160 \ \si\kPa

Given:

T_1=50^{\circ}C

P_1=180kPa

V_1=9m/s

D=0.50m

T_2=100^{\circ}C

P_2=160kPa

Find:

Determine the volume flow rates of water at the inlet and exit, the velocity at the exit, and the mass flow rate.

Solution:

Using Table A-1, gas constant (R)=0.4615 kJ/kg K

\dot{V}_1=A_cV_1=\frac{\pi D^2}{4}V_1=\frac{\pi (0.50)^2}{4}(9)=1.7671\frac{m^3}{s}

\dot{m}=\rho_1A_cV_1=\frac{P_1}{RT_1}\frac{\pi D^2}{4}V_1=(\frac{180}{0.4615\times(50+273K)})(\frac{\pi(0.50)^2}{4})(9)=2.1338279 kg/s

\dot{V}_2=\frac{\dot{m}}{\rho_2}=\frac{\dot{m}}{\frac{P_2}{RT_2}}=\frac{2.1338279}{(\frac{160}{0.4615\times(100+273K)})}=2.29572m^/s

V_2=\frac{\dot{V}_2}{A_c}=\frac{2.29572}{(\frac{\pi(0.50)^2}{4})}=11.69m/s

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Thermodynamics Copyright © by Diana Bairaktarova (Adapted from Engineering Thermodynamics - A Graphical Approach by Israel Urieli and Licensed CC BY NC-SA 3.0) is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book