22

Question 1

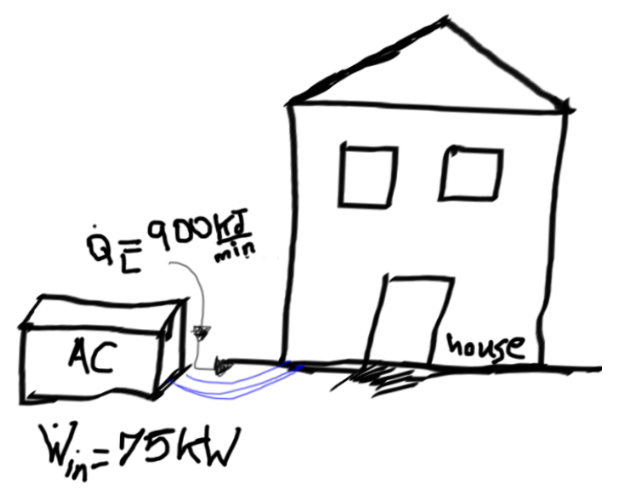
A cooling system is being used in order to decrease heat gradually from a house at a rate of 900 kJ/min while drawing electric power at a rate of 75 kW.  Determine the COP of this system and the rate of heat transfer to the outside weather.

Screen Shot 2015-08-19 at 2.42.39 PM\dot{Q}_\text{L} = 900 \ \si\kJ/\si\min
\dot{W}_\text{in} = 75 \ \si\kW

Given:

\dot{Q}_L=900\frac{kJ}{min}

\dot{W}_{net,in}=75kW

Find:

Determine the COP of this system and the rate of heat transfer for the outside weather.

Solution:

The COP of this system

COP_R=\frac{Q_L}{\dot{W}_net,in}=\frac{900\frac{kJ}{min}}{75kW}\times(\frac{1kW}{60\frac{kJ}{min}})=0.2

The rate of heat transfer for the outside weather.

\dot{Q}_H=\dot{Q}_L+\dot{W_{net,in}}=(900)+(60\times75)=5400kJ/min

 

Question 2

Through the isothermal heat addition process of Carnot cycle, amount of hear, 750 kJ, was added to a fluid from a source at 250^{\circ}C. Determine the entropy change of the working fluid, the entropy change of the source, and the total entropy change for the process.

Given:

Q_{in,fluid}=750 kJ
T_{source}=250^{\circ}C=523K

Find:

Determine the entropy change of the working fluid, the entropy change of the source, and the total entropy change for the process.

Solution:

\Delta S_{fluid}=\frac{Q_{fluid}}{T_{fluid}}=\frac{750}{523}=1.434\frac{kJ}{K}

\Delta S_{source}=\frac{Q_{source}}{T_{source}}=-\frac{Q_{out,source}}{T_{source}}=-\frac{750}{523}=-1.434\frac{kJ}{K}

\Delta S_{gen}=\Delta S_{fluid}+\Delta S_{source}=1.434-1.434=0

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Thermodynamics Copyright © by Diana Bairaktarova (Adapted from Engineering Thermodynamics - A Graphical Approach by Israel Urieli and Licensed CC BY NC-SA 3.0) is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book