Skill Practice: Tackling Longer Readings

It’s easy to feel overwhelmed when a professor assigns you 50+ pages of reading, but you can learn to manage these larger reading assignments by using a few strategies and asking yourself some important questions.

• Look at the section headings and chapter organization.
  • How is the reading organized?
  • What type of a reading is it?
  • How many sections are there?
• Consider your purpose.
  • Why are you reading this chapter? Will you have to discuss it in class, use the information on the test, or do you have a different purpose?
  • Are certain sections of the reading more important to you (or your professor) given the purpose above?
• Pace yourself.
  • How long will it take you to read the assigned pages? (Think about your actual reading speed and allot a realistic amount of time.)
  • How can it be divided into smaller, more manageable chunks?
• Take notes and annotate.
  • Given your purpose, what kind of notes or annotations should you make? Should you underline key terms, write questions in the margins, etc.?
• Summarize and reflect.
  • What did you learn?
  • How do the different sections of the reading fit together?
  • What parts are still confusing or difficult for you?

With longer reading passages that you may have read over several days, it’s important to follow all these steps. For example, taking notes will help you remember what you’ve read and easily review it, and summarizing will help you pull all the information together.

Think about these steps as you tackle the next reading passage which is over 4,000 words. Imagine your professor has asked you to write a summary of this reading and to be prepared in class to discuss what you learned.

Pre-Reading

Reading 4: Designing for People ^[1]

Everything that is designed comes into contact with people at some point. This is mostly through the use of a design, but people are also involved in less direct ways, such as manufacturing, installation or maintenance. Design failure very often occurs because of designers overlook the significance of the users, builders, or other people. A consequence of the involvement of people is the complexity they bring. Just consider the numerous variations of any object around you. Why are there so many shapes of cup, of mobile phones or of cars? Why can one person seem to operate an object easily while other people find it hard? And why can’t anyone solve the problem of uncomfortable seats on an airplane?

This variation and complexity arises from differences between individual people. People are not all the same and their behavior is certainly not predictable. Here are a few key variations a designer might consider:

• People vary physically, meaning that design for people has to take account of a wide range of sizes, shapes and adjustments.
• People have different preferences and thoughts, meaning that what they feel about design and how they interact with it varies considerably.
• People have a range of circumstances and contexts (family, friends, employment, etc.).
• People have different experiences and knowledge, which means that a designer might have to make a range of assumptions.

All of these variations mean that designing for people can be a complex process. Dealing with this complexity is a central part of design. In this section you will look at these variations and complexities in greater detail, but this section starts by considering one obvious variation – the physical sizes of people. You will use this variation to explore how design can blend a variety of analytical and creative approaches to respond to design drivers.

4.1 People and variation

Start by considering how you would begin designing an object that has to ‘fit’ to people, such as a simple desk or table. People using it will vary in size and these differences might be quite extreme (at the time of writing, the tallest person recorded had a height of 2.72  meters or almost 9 feet and the shortest woman alive is 628 mm or 2.06 feet tall). What sizes should you start with? Is a single height acceptable? If not, how many sizes might you need?

Solving the problem of human variation is not a simple exercise. If you design a product to suit people at a particular height, you may then be limiting access for other people. Figure 13 shows a typical ticket machine in the UK. If you have used a machine like this, you might have wondered whether the designers took human shape and sizes into account. You may have to uncomfortably bend over to use the machine – or you might have found the machine perfectly comfortable to use. It all depends on your point of view.

At some point decisions are required to be made about the properties of a design in progress. The ticket machine shown in Figure 13 had to be designed in terms of height, width and depth, in order for it to be manufactured. In making these decisions, however, you might solve the problem for some people but make it worse for others. Knowing how to think about difficult decisions like these can be useful as a designer. Because several different factors are involved, you need to use particular ways of thinking through this type of design problem.

4.2 Practical variation

One way to approach a design problem is to use your own knowledge and experience. You may not be a furniture, car, or airplane designer but you probably have considerable experience sitting down! Making use of this personal knowledge might seem trivial, but it is the start of all creative problem solving. The key is turning this personal knowledge into information you can use in any design process.

What you have done in Activity 1 is to measure something that already exists. You have an existing desk and you have given a value to a property of it. Now, when you talk to other people about your desk, you’ll be able to state the height in a way that they will understand.

Before you take this measured height as the perfect desk height, it is worth checking this assumption. Once again you will use a practical method to do this.

This technique is called design prototyping, where you create a quick physical mock-up of a design idea in order to test some aspect of that idea. It is exceptionally useful because it is quick and simple, and you get instant feedback on the problem you are exploring. Almost all design problems can be prototyped (even systems and processes) and this is a key method in any design engineer’s toolkit.

The prototype you have just made can also provide two types of information. When you increased the height of your desk you might have noted whether it felt uncomfortable and whether this discomfort is acceptable or not. Or you might have compared two heights to see which one is more (or less) comfortable. You are no longer only measuring height; you are also making judgements about the desk at these heights. In both cases you now have new items of information, and they are of different types. The height of the desk is quantitative information, while what you think and feel about the new height is qualitative information.

The height you are working with is fine for one person (you!) and it is possible to imagine that other people of about your own size might also be quite happy with that height. But the general problem is: what height should you use to design a desk to ‘fit’ people? In other words, you are interested in finding a height that many people will find comfortable, and one way to do this is to find out how many people might find a particular height comfortable.

To expand the problem beyond your own experience, you need to use other techniques.

4.3 Numerical variation

When it comes to designing for large numbers of other people, it becomes impractical to ask every individual what they think. But the same practical methods you have just used can be scaled up using statistical methods. For example, from Activity 2 you now have a desk height that suits you, and you might assume that most people of your size will also like that desk height. So now you need to know how many people are the same size as you. For that, you need to make use of statistics.

Before carrying out a detailed analysis of any dataset, it is a good idea to examine the values to see if any patterns or unusual values stand out. You should never ignore data because it is different from what you were expecting, but if a dataset does contain surprising values, it is a good idea to question them in case a mistake has been made. You might look for the following:

• missing data – for instance, if you are given a table of data that has obvious unexpected gaps in it.
• false precision – where a number is quoted to the hundredth decimal point and that might not be reasonable given the manner the data was collected or where the data may be rounded up or down to such an extent that it is not useful for the intended purpose.
• Dubious data – for instance a data point may be surprisingly large or small. This could be due to simple errors, such as a misplaced decimal point.
• Coded values, where the data provider may have used a code to indicate something, such as a missing value.
• Constraints – for instance, there may be some good reason why the data has to lie within a particular range.
• The presence of outliers – single values that are very different from the rest of the dataset.

Having checked that your dataset looks valid, you can perform calculations on it. For example, it may be useful to find the average of a set of values.

You have probably come across the idea of an average before, and you may also know that there are different kinds of averages. The most useful types of averages are usually the mean and the median.

Finding the mean of a dataset: To find the mean of a set of numbers, add all the numbers together and divide by however many numbers there are in the set.

Finding the median of a dataset: To find the median of a set of numbers:

• Sort the data into increasing (or decreasing) order.
• If there is an odd number of data values, the median is the middle value.
• If there is an even number of data values, the median is the mean of the middle two values.

These basic statistical tools are useful when it comes to designing for people.

Before you move on from this activity, it is important to realize that this is not just a theoretical exercise. The example height used in part (d) of the answer to Activity 3 produces a real value (for example, for me it’s 44 mm) that can be used practically. As you know, small differences (even smaller than 44 mm) can have a significant effect. It is important to be aware of what the values used actually represent when you use any mathematical methods in design engineering.

4.4 Using numbers to design

To move forward with the desk problem, you needed to know how many other people might be your height. You found a certain desk height acceptable and might reasonably assume this is a good size for every one of the same height. But how might you find out how many other people are your height?

There are many sources of data on sizes, from the very general (such as people’s heights) to the exceptionally specific (such as NASA’s guide to the sizes of things in space). Two key sources where a range of human data and information can be found are the British Standards Institute (BSI) and the Health and Safety Executive (HSE). The data they provide about the size and shape of people is called anthropometric data, which consists mainly of physical characteristics and measurements. These data values are derived using statistical methods that allow generalizations to be made about human characteristics, which can be used to inform the design process.

Making use of these datasets and applying knowledge of how people interact physically with objects can be a complex process and is even a separate discipline. Ergonomics is the study of physical aspects of the human body, such as size and mechanical performance, and how these can be applied to the real world. For example, in car design and manufacture, the design of a car interior has to take account of significant variation of human shape and size, and hence the range of adjustments that can be made to a car seat, seatbelt, steering wheel, etc. And that’s before you consider how these adjustments relate to one another, or are operated mechanically.

One useful way of presenting data, which is particularly useful for anthropometric data, is to create a histogram. Histograms offer a convenient way of presenting data to make it easier to read for a particular purpose. Instead of using a continuous spread of data, you divide it up into ‘buckets’ (often referred to as ‘bins’ or intervals) and sort items into them. For example, you could think of it as a way of sorting people into height ranges and then working out what proportion of people are in each range. Bar charts are similar, but can be used to represent categories of things that aren’t necessarily numerical.

4.5 Visualizing numbers

Histograms are used to plot quantitative data, with ranges of data grouped into intervals. For instance, Figure 14 shows a histogram of 200 people using height ranges of 20 mm, with heights measured to the nearest 1 mm. Notice that the values on the horizontal axis are continuous – the first bucket goes from 1600 mm to 1619 mm, the second from 1620 mm to 1639 mm, and so on. The vertical axis shows percentages. The area of each bar represents the percentage of people whose height falls in that range, and the sum of all the areas would equal 100%.

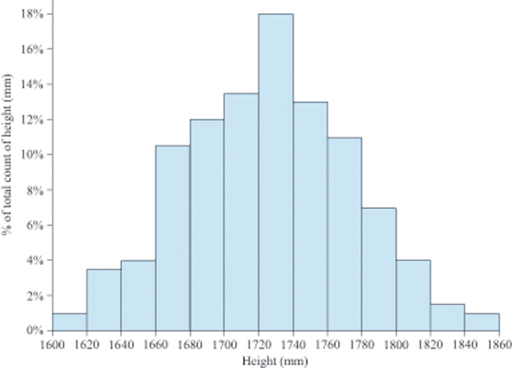
For this data to be really useful you need a few more data points, and the ranges would be more useful if they were smaller, as in Figure 15. Based on the data in Figure 14, 18% of the population are in the 1720–1739 mm bucket. This means that 18% of people are between 1720 mm and 1739 mm tall. Another way to write this is by using a tolerance symbol (±), so in this case the tolerance is (to a good approximation) 10 mm above or below 1730 mm. This can be written as 1730 (±10) mm.

Histograms and bar charts

The following section provides further information about histograms and bar charts.

Looking at Figure 14 it seems that quite a few people might not be entirely happy with any one specific desk height. A next step might be to work out a bit more accurately what sort of height ranges would be acceptable to suit as many people as possible.

But there are a few big assumptions in what you have just done.

Firstly, it was assumed that there is a link between a person’s height and their preferred desk height. This might not be a valid correlation – arm length or sitting height might give a more appropriate relationship. Or there might not be a reliable human measure to use in this instance.

Secondly, it was assumed that 20 mm is a suitable division for the buckets in Figure 14. It is possible that people in both the 1720–1739 mm and 1740–1759 mm buckets have exactly the same preference, and that 40 mm buckets would be appropriate.

4.6 Designing for people using numbers

Designing for people can be a complex process for some very simple reasons. Designing the height of a desk for one person might be relatively straightforward, but making that same desk suit lots of people is quite difficult because of the variation in human sizes.

Playing with data

The data you have just been looking at could now be added to hundreds, thousands and even millions of additional data points. In fact, some of the anthropometric data used in the British Standards is collected from entire country populations.

Each time another point is added, the shape of the histogram will change slightly. If we had enough data points we could even imagine the histogram being quite a smooth shape (Figure 16).

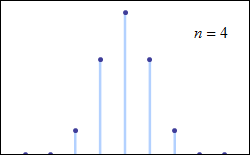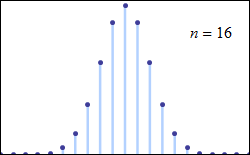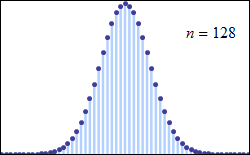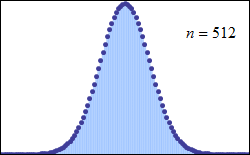
The smooth curve in Figure 16 is called a distribution curve. This is one of a number of different types of representation of data that is useful to be aware of. It’s different to the histogram because it is smooth (continuous) and is not divided into individual (discrete) ranges of data.

It is simply useful to see the shape of this data and to realize that a visual representation of information can be just as useful as a mathematical one.

By playing with this data visually, you can see some useful things about any design problem. In particular, you may now be able to visualize just how exclusive some design decisions can be; the decision to use a particular height might exclude a whole section of a population from that product. Clearly, seeing the world from a range of different users’ perspectives can have a dramatic effect on the design process.

4.7 Summary of Section 4

It is no trivial matter to physically design something for people to use. The ergonomics of design engineering can be a very complex aspect of design, but simply being aware of people’s sensitivity to physical variation can be useful as a designer. Even better, perhaps, is to realize that placing people at the center of any design process can help you to tackle difficult ‘human’ design problems.

As you have seen, designing for the ‘average’ or majority in a population means you often ignore other large parts of the population. This can have a particularly significant effect on population groups that lie outside the average groupings, such as children, older people or wheelchair users. One way of approaching this is to design in order to suit as many people as possible, or even for all people in any population. This is known as inclusive or universal design.

Taking this approach for the desk example, the challenge is to create a surface that is suitable for as much of the population as possible. This then becomes the new design driver – to solve the problem of a desk that is adjustable to suit a wide range of users. This changes the original design question, but it also expands the potential user market. Remember, you started considering only your own height and preference (a market of 1 person) – designing for a wider range of the population automatically means creating a more accessible product for all users of that design. In fact, most desks attempt to do precisely this and have adjustable feet to ensure that they are adaptable to as wide a range of people as is reasonably possible.

But physical variation is not the only human issue a designer must consider – the attitude and thinking of people is also a hugely important area of study. Like ergonomics, this is almost a whole discipline in itself, called human factors. It deals with how people think, react and interact with products, systems and services. As with ergonomics, it is essential to recognize how important this can be for the success of any design. Research shows that the way people feel about a design has a huge impact on how they use that design – whether they persist with it, use it correctly or simply ignore it.

Take your desk height as an example. If the desk were to be fully prototyped using different materials, you might feel very differently about each height depending only on the material. Some research even shows that your posture, or how you sit, changes depending on how much you like your desk!

Similarly, the design of instrument and control panels for complex systems has to consider how people read, use and interact with them – the design cannot only consider functional requirements. Modern cockpits in large commercial airplanes, for example, are designed specifically to take account of how people use and interact with the instruments; Figure 17 shows an example. Designing with the user in mind throughout the process is known as user-centered design.

By placing the user of a design at the center of the design process, the focus of the project shifts from what is often a static perspective (considering certain aspects only) to a more active view of design (how certain aspects work in the real world). Unfortunately, changes in airplane design came only after a series of major failures, where it was recognized that changing the way information was presented to pilots would allow them to make better decisions. The lesson from this is simple – never ignore the user in any design project.

This section has guided you through a short design process. It started with a general exploration of desk height; you then made use of direct knowledge, then tried something to test your ideas and finally checked what you did. If you were to repeat this process and improve the starting question, you would be able to repeat and improve what you did each time. This repetition and improvement is known as iteration, and it is the essence of design – starting somewhere, thinking about it, doing something, then checking it, and repeating the whole cycle until it works the way it needs to.

At each stage you also used a range of types of thinking and processes, both analytical and creative, to ‘think through’ the problem one step at a time. Each time you did this, what you found informed the next stage in the process – all with the overarching aim of responding to the original question posed. Design is not simply doing one thing or applying one kind of approach – it is a process that incorporates a range of skills, attitudes and approaches.

Conclusion

Hopefully your existing ideas of what design is have been challenged so you now think of design in other ways too. You have seen that design is more than simply choosing the shape and appearance – it’s a fundamental human ability to take existing conditions and change them with a clear purpose.

Design responds to real world situations and challenges, most of which are driven by human needs and desires. These design drivers are major factors in motivating designers but designing for humans is still unquestionably a difficult task.

You have also been introduced to some numerical methods that can be applied in design, showing that it’s not only creative thinking that’s necessary – good analytical thinking is needed too.

The key to good design is knowing when to apply each of these to best effect in the design process. As a design engineer, you make use of both creative and analytical thinking, taking human imagination and creativity and making it a working reality.